基于DEM-SPH 流固耦合的冰区船舶快速性预报

吴 捷 刘 璐 田于逵 季顺迎

（1. 大连理工大学 工业装备结构分析优化与CAE 软件全国重点实验室 大连 116024； 2. 大连理工大学 船舶工程学院大连 116024； 3.中国船舶科学研究中心 无锡 214082； 4. 深海技术科学太湖实验室 无锡 214082）

0 引 言

极地船舶在冰区破冰航行过程中需要考虑船舶快速性能，而极地海冰和海水组成的流固混合场对船体结构的快速性能具有重要影响[1]。船舶的快速性一般研究航行阻力和推进力平衡状态下的主机功率、螺旋桨转速和扭矩等参数，同时考虑船舶航行过程中的船体结构、推进装置与流体的流固耦合作用[2]。对于冰区航行的极地船舶，还需考虑海冰与结构的相互作用，主要包括海冰与船体结构，以及在船体周围伴流场作用下，破碎海冰同螺旋桨和推进器相关结构产生的碰撞作用等[3]。因此，极地船舶的快速性研究需要充分考虑船体和推进器结构在冰水混合场中受到的作用力，对船舶在特定航速下的阻力和推力等力学参数进行预报分析，从而获得极地船舶快速性的相关参数。

结构在浮碎冰区航行过程中主要与碎冰发生碰撞、摩擦等作用，会受到碎冰密集度、形状与尺寸等参数的影响[4]。由于结构在浮碎冰区的运动会引起自由液面兴波，因此当碎冰密集度较低时，结构周围碎冰会在波浪作用下提前被排开，导致结构与碎冰的作用次数减少，进而降低了结构的航行阻力；当碎冰密集度较高时，结构首部处的碎冰会在周围碎冰的持续作用下与结构同步运动，形成类似附连水效应，从而增大了结构的航行阻力。

在破冰船开辟的冰区水道中，一般存在尺寸较小的海冰，其会在螺旋桨附近流场的作用下，同桨叶与局部结构发生高速碰撞、切削作用[5]。然而，针对碎冰受到流场扰动并与结构相互作用的物理过程的研究目前并不充分，该场景下局部结构的动力响应及运动受到的海冰影响也不明确。此外，高速运动的结构会对海水形成一定冲击作用，所造成的强烈流场波动会提前导致海冰的裂纹扩展、断裂与破碎，从而影响海冰与结构的相互作用过程，进而受到海水的流固耦合作用。目前还缺少流场影响下的海冰与结构相互作用试验研究，相关的数值模型研究也极其匮乏。

数值模拟方法是研究极地船舶与海洋工程结构同海冰相互作用、冰载荷、冰激结构响应的重要手段。近年来，有限元[6]、离散元[7]、近场动力学[8]等方法在海冰破坏过程模拟中应用广泛。离散元方法（discrete element method，DEM）对脆性材料破坏过程的模拟具有较高的计算效率，其对材料破坏过程中的裂纹扩展、破碎特性等均能进行出色的模拟[9-10]，故在海冰与结构相互作用的数值模拟中受到了广泛关注。结合结构的有限元方法还可建立海冰与结构相互作用的离散元-有限元耦合模型，在船舶、风机等结构的冰激响应和振动特性分析中取得了良好效果[11-12]。另外，在船体结构与海冰的相互作用数值模型中，还可进一步结合海水的计算流体力学方法，分析流场影响下的海冰与结构相互作用过程[13-14]。

然而，各方法之间由于收敛时间步长不同，会导致计算时间尺度差异问题，在不同时间步长上的参数传递效率较低；不同形态海冰单元与流体存在复杂形状的流固界面，传统方法计算海冰与流体间耦合作用的效率较低。因此，海冰与结构的相互作用研究中需要考虑海水与海冰、结构的流固耦合作用，建立结构在冰水混合场中航行运动的流固耦合模型，为冰载荷和冰激结构响应计算提供重要的方法基础。

基于拉格朗日粒子的光滑粒子流体动力学（smoothed particle hydrodynamics，SPH）方法在自由液面、大变形模拟中具有明显优势，在海洋工程、化工搅拌等领域中应用较为广泛[15]。在DEM与SPH 的耦合模型中，不仅需重点考虑固体单元截断流体粒子支持域造成相关物理量计算不准确的问题，还需考虑不同时间步长引起的计算参数传递问题[16]。固体粒子模型将边界抽象为由若干层固定不动的粒子所组成的粒子墙，是SPH 中使用最为广泛的边界构造方法[17-18]。但由于固体粒子需消耗大量的计算资源，故采用粒子构造边界的方法难以适应不同形态固体颗粒的模拟，而通过光滑函数的积分正则化修正粒子密度和速度，可有效构造复杂的固体边界并计算其与流体粒子的相互作用[19]。采用若干层固体粒子构造固体边界，并假定固体粒子的密度等物理量与流体粒子相同，继而将流体粒子的光滑函数导数拟合为与固体边界距离的函数，在实际的SPH 模拟中即可直接采用该拟合函数计算流体粒子受到的边界作用[20]。以上SPH 方法中的流固边界计算方法为流体粒子与固体边界的快速计算研究奠定了良好的基础，据此可进一步发展海冰与海水的DEM-SPH 耦合模型。

本文分别采用离散元方法和光滑粒子流体动力学方法模拟海冰和海水，并建立冰水耦合的DEM-SPH 模型，对刚性船体和螺旋桨结构进行简化建模，建立合适的流体便捷模型，模拟并分析船舶航行过程中所收到的总阻力与螺旋桨推力情况，反推出自航所需的螺旋桨转速，进而分析船体在冰区航行过程中的快速性。

1 基于DEM-SPH 的冰水耦合模型

本文采用基于平行黏结模型的离散元方法模拟海冰与结构作用过程中的断裂和破碎，并考虑海冰破裂后碎冰块之间的接触、碰撞和摩擦作用。采用SPH 方法模拟海水，同时考虑固定计算域边界处的速度和压力边界条件，实现固定流体域上的海水流动模拟。采用SPH 粒子与固定粒子边界相对运动的拟合项，直接计算固体与流体之间的相互作用力，建立海冰与海水耦合的DEM-SPH 模型。

1.1 海冰离散元方法

海冰离散元方法基于海水离散元模型（图1），其中采用密排六方形式的球体单元表征海冰，球体单元之间可传递黏结力、接触力等，如图1（a）所示[21]。黏结力表示连续海冰内部的作用情况，通过对黏结力施加一定的失效准则，连续海冰可发生断裂、破碎等动力学过程；接触力则表示海冰发生破坏后由接触、碰撞产生的相互作用。

图1 海冰离散元模型

平行黏结模型是离散元方法中实现材料破坏模拟的经典模型，其将2 个球体胶结在一起，不仅可传递力，还可传递力矩。如图1（b）所示，平行黏结模型将相邻单元之间的黏结作用简化为梁或黏结圆盘[22]，采用梁模型计算单元之间的法向和切向作用力，如式（1）所示：

式中：Fb为单元之间的黏结力，N；Mb为单元之间的黏结力矩，N·m；Fbn和Fbs分别为单元之间的法向和切向黏结力，N；Mbn和Mbs分别为单元之间的法向和切向黏结力矩，N·m。

此处可采用增量的形式计算黏结力和力矩，如式（2）所示：

式中：ΔUn和ΔUs分别为单元间相对位移的法向和切向分量，m；Δθn和Δθs分别为相对转动位移的法向和切向分量，m。各参数表达式见式（3）：

式中：u为平动速度，m/s；ω为转动速度，rad/s；Δt为时间步长，s。

根据三维梁理论，单元之间的最大拉伸σmax和剪切应力τmax见式（4）：

式中：A为黏结圆盘的横截面积（A=πR2），m2；J为黏结圆盘的极惯性矩（J=πR4/2），m4；I为黏结圆盘的惯性矩（I=πR4/4），m4。

在单元黏结作用过程中，若黏结圆盘的最大拉应力超出其法向黏结强度，或最大剪应力超出其切向黏结强度，即σmax＞或τmax＞，则该黏结作用失效，从而可模拟海冰材料内部的断裂和破坏过程。和满足Mohr-Coulomb 准则，如图2 所示。同时，在基于平行黏结模型的离散元模拟中，和受到单元尺寸的影响，故需通过材料的典型力学试验进行校核，如三点弯曲和单轴压缩试验。

图2 法向和切向黏结强度满足Mohr-Coulomb 准则

通过海冰材料的三点弯曲和单轴压缩数值试验，可建立海冰离散元试样的材料强度与黏结强度的关系式[23]，见式（5）：

式中：σf为海冰的弯曲强度，MPa；hi为海冰厚度，mm；R为球体单元的半径，mm。

海冰发生破坏后，单元之间的黏结作用转变为接触摩擦作用，这里采用球体单元的线性接触模型计算接触力。该接触力可分为由刚度导致的弹性力Fnce和阻尼导致的黏性力Fncv。法向的接触力Fnc可表示为式（6）：

式中：δn为法向重叠量，m；Cn为法向阻尼系数；δn为单元间接触点处的法向相对速度，m/s；Kn为两相邻单元间的法向刚度（单位是N/m），表达式见（7）：

式中：E为海冰的弹性模量，Pa；i和j表示两相邻单元的编号。

法向阻尼系数Cn可表示为式（8）：

式中：mij为等效质量，mij=mimj/(mi+mj)，kg；ξn为无量纲阻尼系数，为恢复系数。

切向接触力Fcs可表示为式（9）：

式中：Ks为两相邻单元间的切向刚度；Cs为切向阻尼系数；t和■分别为切向接触重叠量和相对切向速度的单位向量；δs为切向的接触重叠量，可根据相对切向速度和逐步积分获得；sδ˙ 为两单元接触点处的相对切向速度，m/s；μ为滑动摩擦系数。Ks和Cs分别按照Kn和Cn的一定比例计算，见式（10）：

式中：α和β均为0.1[24]。

单元间的接触力Fc和由切向接触力引起的接触力矩Mc，可表示为式（11）：

式中：n为接触的单位法向量；s为切向上的单位矢量，

考虑每个单元受到的黏结和接触作用，单元的运动方程可表示为式（12）：

式中：Is为球体的转动惯量，Is= 0.4mR2；Fh为流体给海冰单元的作用力，N；Mh为流体给海冰单元的作用力矩，N·m。

1.2 基于SPH的计算流体动力学方法

相比于基于网格的计算流体力学方法，SPH 方法更易于处理自由表面问题以及冰-水或船-水间的固液交界面。因为SPH 方法本身是一种无网格的粒子法，其不需要像传统的网格方法一般引入体积分数来表征自由液面或固液交界面，在计算船冰水耦合问题上相比于传统计算流体力学动力学方法具有一定的优势。同时，相对于传统的弱可压缩格式以及隐式不可压缩格式的SPH 方法，本文采用显式不可压缩格式的SPH 方法求解流体压力，在计算精度与计算效率上找到了较好的平衡点，更易于进行三维大规模数值模拟[25-26]。

SPH 方法可以将连续的场函数进行拉格朗日格式离散。如图3 所示，粒子i处的任意场函数A（ri）见式（13）：

图3 SPH 核函数示意图

式中：r为粒子的坐标；N为粒子相邻粒子的总数；m为粒子的质量，kg；ρj为该粒子的密度，kg/m3；rij为粒子间的相对坐标，可写为rij=ri-rj；h为光滑长度；W(rij,h)为核函数，其是与粒子间距离有关的偶函数[27]。

这里采用三次样条曲线方程作为核函数，见式（14）所示：

式中：q为正则化粒子间距离，q=rij/h。

粒子i处的任意场函数梯度 ∇·A(ri)可表示为式（15）：

式中：rij为粒子间的距离（rij=|rij|=|ri-rj|），m；∇iWij为核函数梯度。

在不可压缩格式下的流体拉格朗日型Navier-Stokes 方程可表示为式（17）和下页式（18）：

式中：u为流体的速度，m/s；P为流体的压力，Pa；v为流体运动黏度，对于海水，可以取v=10-6m2/s；g为重力加速度，m/s2。

由于不可压缩流体密度保持恒定（即 ∇·u= 0），Navier-Stokes 方程可以近似表示为式（19）和式（20）：

式中：ρi=ρj=ρ0，ρ0为不可压缩流体的密度，kg/m3；黏度项 (v∇2u) 可表示为式（21）[28]：

式中：uij为粒子间的相对速度（uij=ui-uj），m/s；η为保证分母不为0 的较小值，η=0.1h。

采用两步预测修正的方式可获得SPH 粒子的压力泊松方程[29]。在预测步，计算只受黏度项及重力项影响下的粒子速度，粒子经过预测步后的速度u*可表示为式（22）：

式中：Δt为运动积分的时间步长，s；un为粒子在当前时间步的速度，m/s；粒子下一时间步的速度un+1可由预测步状态进行压力梯度修正得到，见式（23）：

基于速度散度为0 的条件（即 ∇·un+1= 0），可将上式转化为式（24）所示压力泊松方程：

为了提高计算效率，采用可显式计算的近似解计算压力泊松方程[30]，粒子下一时间步的压力可表示为式（25）：

式中：Aij可表达为式（26），Bi可表达为式（27）：

式中：u*ij为2 个SPH 粒子在预测步中的相对速度（u*ij=u*i-u*j），m/s。

使用上式计算所得的粒子压力Pni+1带入控制方程中，可以得到下一时间步粒子的速度，下一时间步粒子的位置rn+1可表示为式（28）：

为施加固定流体域上的边界条件，采用设置虚粒子层的方式构建缓冲区，从而可设置流体的出入口边界[31-32]。流体的出入口边界模型大致分为压力出入口边界、速度出入口边界、开放边界。3 种边界均采用虚粒子方法在边界处形成缓冲区，避免流体计算域内的粒子核函数计算域缺失，虚粒子缓冲区如图4 所示。

图4 边界缓冲区示意图

在本模型中，出入口边界的几何法向均指向真实计算域内，并在负法向上添加虚粒子以构建缓冲区。缓冲区内虚粒子初始间距与真实粒子一致，且缓冲区宽度需大于2 倍光滑长度[33]，即最少也需2层虚粒子。通过缓冲区内的虚粒子与真实粒子的位置和物理量交换，实现计算域边界处速度、压力的边界条件。

1.3 DEM-SPH流固耦合模型

为得到扩展多面体颗粒和SPH 粒子之间的耦合作用，本文将单元视为一种刚性固体边界，并通过拟合的方法得到两者之间的耦合作用。对于SPH 粒子核函数计算域被固体边界截断的情况，在边界外紧密排列了足够多的固定边界粒子，进而模拟边界对SPH 粒子的作用[20,34]，如下页图5 所示。固定粒子的间距与SPH 初始粒子间距相同，固体粒子质量和密度也与SPH 粒子相同，速度为0。边界粒子的压力见式（29）：

图5 SPH 刚性边界模型

式中：PB为边界粒子的压力，Pa；d为SPH 粒子到边界的距离，m；nB为边界面法向。

此状态下，边界粒子对SPH 粒子的作用力可表示为式（30）：

式中：rib为SPH 粒子与边界间距离，m；uib为SPH 粒子与边界间的相对速度，m/s。

式（30）右侧第1 项可简化为边界对SPH 粒子的法向作用力，见式（31）：

式中：F∇W可表示为式（32）：

式（30）右侧第2 项可简化为边界对SPH 粒子的切向作用力，见式（33）：

式中：F∇W、F∇W/r只与h/Δx及SPH 粒子到边界的正则化距离q有关。此处：q=d/h；h/Δx=1.25。F∇W、F∇W/r的关系曲线如图6 所示。

图6 F∇ W和 F∇ W/r 与q 的关系曲线

对F∇W、F∇W/r和q之间的关系进行多项式拟合[35]，见式（35）、式（36）：

SPH 方法中的粒子运动均为显式积分，因此计算过程中可看作流固界面上存在一对排斥力分别作用于流体粒子和固体界面，固体粒子所受SPH 粒子作用力之和即视为固体单元受到的流体作用力。

2 冰区船舶的快速性预报分析

由于冰区船舶的快速性需要同时考虑海冰和海水的耦合作用，采用流固耦合算法实现难度较大，目前尚未有相关的研究报道。为此，本文基于海冰离散元方法建立的DEM-SPH 耦合方法的优势和特点，形成了冰区船舶快速性预报的方法流程。该模型分别对船舶在冰区的航行阻力和推进力进行模拟：在船舶航行阻力的计算中，模拟船舶在一定航速下的航行阻力；在推进力的计算中，模拟螺旋桨在不同转速下的推进力。通过拟合的方式匹配航行阻力和推进力，从而预报船舶在特定航速下实现自航所需的螺旋桨转速。

2.1 船舶快速性分析的数值计算模型

为分析船体结构在不同航行工况下的自航螺旋桨转速，本文在模拟中使船体保持不动，约束其六自由度运动，并给定流场速度以模拟不同螺旋桨转速下船体结构所受的强制力，进而拟合出强制力为0 时的螺旋桨转速，该转速即为所需自航条件下的螺旋桨转速。为了考虑船冰间的相互作用，文中采用DEM-SPH 耦合的方法模拟船体结构-海冰-海水三者间的相互作用。此时，若仍同时考虑船体冰阻力和螺旋桨推力的计算，则所需SPH 计算精度较高、计算规模过大，目前较难实现，故将船体快速性预报分为2 个模拟算例。

（1）船体航行阻力模拟

首先计算船体冰区航行过程中的总阻力，其中包含了冰阻力和水阻力。此时流场包裹全船，但计算精度相对较低，在计算过程中螺旋桨并不旋转，具体计算设置如图7 所示。

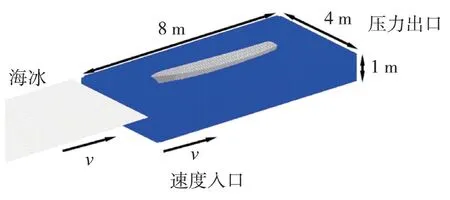
图7 阻力计算模型示意图

计算过程中，船体结构保持不动，通过前部的速度入口及尾部的压力出口得到稳定的流场，其中，速度入口处流体速度等于该工况下的船速；海冰从流体入口处进入计算区域，在进入计算区域之前，其速度保持不变并与流体入口速度相同。

（2）螺旋桨推力模拟

在计算得到船体航行总阻力后，将SPH 计算域缩小，只考虑船体尾部螺旋桨附近的流场计算，其余位置的流场使用恒定流场代替，如图8 所示。在SPH 计算域外部，海冰受恒定流场的拖曳力和浮力作用，进入SPH 计算域后才改为计算流体与海冰单元间的相互作用。同时，考虑速度入口与压力出口并不对称，将底部流场边界设为开放边界，两侧边界设为速度入口边界，其速度大小及方向与该工况下的船速相同。

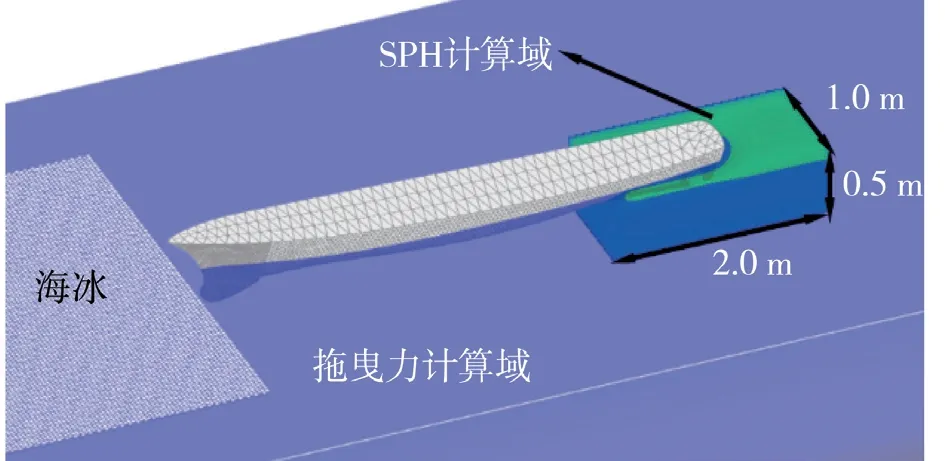
图8 推力计算模型示意图

在该模型计算中，需计算得到不同螺旋桨转速下螺旋桨受到的推力及推力减额情况。其中，推力减额被认为是由于船体受流场阻力的增加引起的，因此需计算零转速下船体所受的流场作用力，并与高转速下所得计算值进行对比，得到对应转速下的推力减额情况。

船体模型采用DTMB 5415 单体船型，配备双轴桨推进，螺旋桨旋转方向如图9 所示。

图9 船体模型示意图

计算工况按照缩尺比1∶30 设计，船长4.733 m、宽0.634 m、吃水0.205 m，海冰及流场计算参数列于表1 中，相关计算参数均为模型尺度下的参数值。

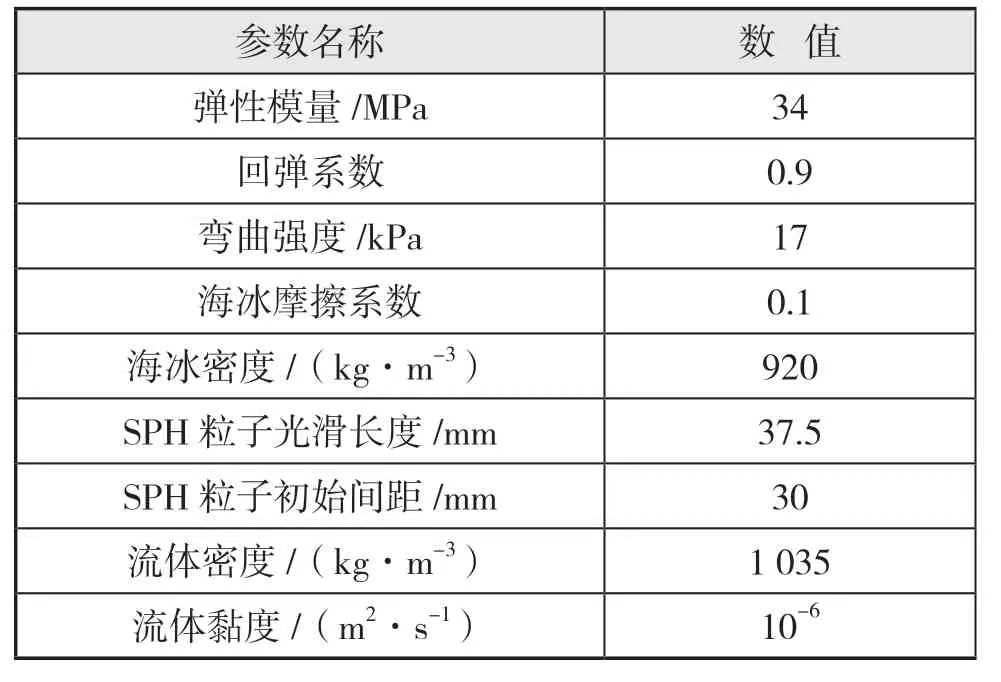
表1 船体冰阻力计算参数

2.2 浮冰区船舶自航下的螺旋桨转速分析

基于上述DEM-SPH耦合模型及边界条件模型，建立了船体结构冰区航行阻力计算模型，其中浮冰厚度为0.033 m、尺寸设为1 m × 1 m、密集度为80%，与模型试验保持一致；航速设置为0.282 m/s，并设置了3 个螺旋桨转速，分别为100 r/min、200 r/min、400 r/min。船体破冰结果如图10 所示。

图10 船体在浮冰区航行过程模拟

两侧浮冰基本没有发生破碎的情况，中间的浮冰因与船体相互作用大多从中间断裂，并向船体两侧滑开。由于受到两侧浮冰的限制，船后水道只比船宽稍宽，但其中的碎冰较少。不过，随着船体结构远离，两侧破裂的大块浮冰会再次占据航道，船后远端的航道则基本重新闭合。

船体在破冰过程中受到的阻力情况见图11。其中，10 s 之前由于海冰未同船体结构碰撞，故其阻力主要为流体阻力。可以看出，流体阻力远小于冰阻力，这也与其他学者的模拟结果一致。在进入冰区后，冰载荷呈现较大波动，但总体保持稳定（平均阻力为28.7 N），这说明此时冰阻力主要为船体破冰产生的作用力，破坏后的碎冰对船体的浸没阻力与摩擦力在该工况中占比较小。

图11 船体浮冰区航行的阻力时程

不同螺旋桨转速下的尾部流场模拟结果参见图12。从图中可以看出：随着螺旋桨转速的增加，在螺旋桨和舵桨之间产生高速流场，经过舵桨后的流速明显降低；并且由于浮冰破碎后向两边排开，因此船体底部没有海冰下潜，破碎的海冰与螺旋桨之间不会发生碰撞。

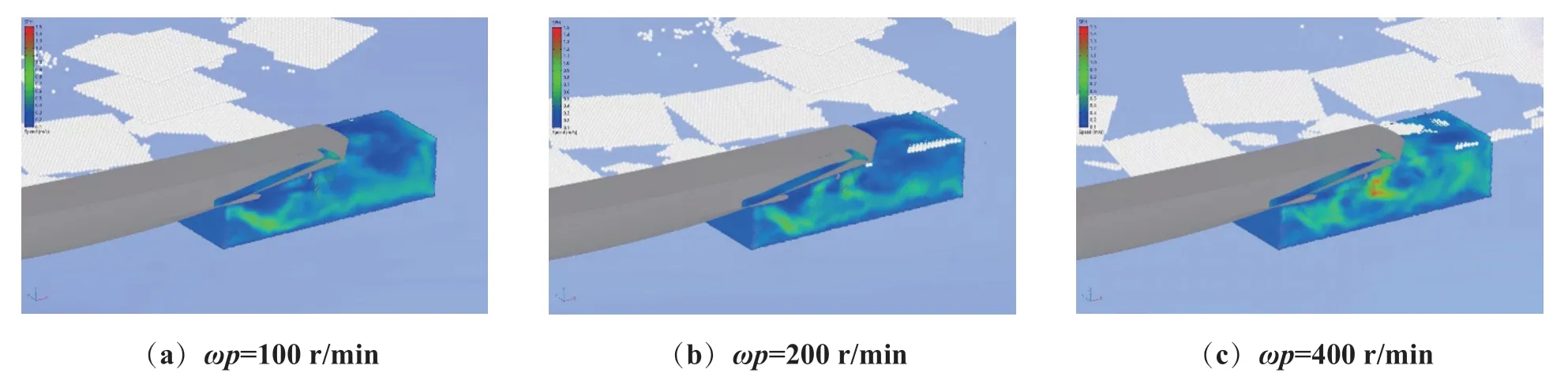
图12 不同螺旋桨转速ωp 下的尾部流场模拟结果

图13 所示为2 个螺旋桨所受的总推力以及各个螺旋桨所受的力矩情况。从图中可以发现：当转速由200 r/min 提高到400 r/min 后，螺旋桨所受推力与力矩都明显增加；对比相应转速下计算得到的流场情况，发现400 r/min 下的螺旋桨后部流场速度也明显提高。计算得到的流场现象与推力统计现象两者一致。

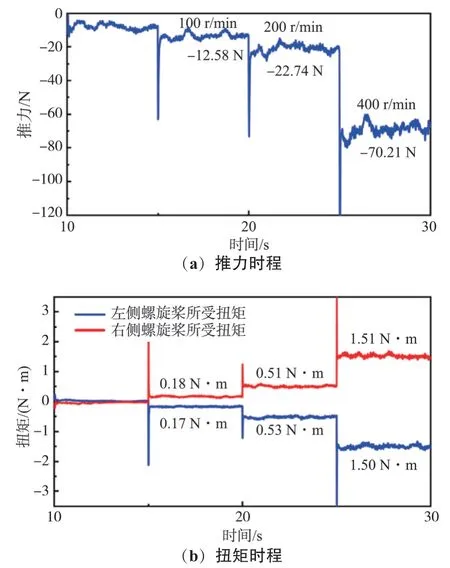
图13 螺旋桨所受推力及扭矩时程

图14 所示为尾部流场对船体结构的作用力以及计算得到的推力减额。从图中可以看出，当转速由200 r/min 增至400 r/min 后，推力减额数值明显提升。从前文分析可知，螺旋桨附近的流场流速增加最为明显，由此可以认为该方法得到的推力减额数值，就是由于流场流速增加所导致的船体阻力增加部分。

图14 不同转速下的推力减额情况

将计算结果统计后列于表2 中，计算出各个转速下的强制力情况；再以强制力为x轴、螺旋桨转速为y轴，对所得数据进行二次拟合，得到的曲线截距即为自航时所需的螺旋桨转速；最后便可得出该工况下自航所需的螺旋桨转速为281.52 r/min，如图15 所示。

表2 浮冰工况中不同螺旋桨转速的计算结果表

图15 通过强制力拟合获得自航转速

通过更改航速计算3 个不同航速工况，将结果汇总于表3 中；同时也统计了不同航速下所需的螺旋桨转速，如图16 所示。

表3 不同航速工况下的计算结果

图16 不同航速下所需的螺旋桨转速

从图中可以发现，随着航速增加，所需的螺旋桨转速也出现明显增加，这主要是因航速增加后，阻力也快速增加所导致。该现象具有一定合理性，在没有试验对比的条件下，可初步认为所用方案可行。

2.3 层冰区船舶自航下的螺旋桨转速分析

本文基于浮冰计算模型建立了船体平整冰区航行阻力计算模型，平整冰厚度与浮冰一致，平整冰区域宽1.33 m、航速设置为0.188 m/s，设置3 个螺旋桨转速，分别为300 r/min、500 r/min、700 r/min。船体阻力计算结果参见图17，其中破冰结果如图17（a）所示。船体破冰后碎冰会向两侧冰层下方运动，因此船尾部航道中浮冰较少。船体航行破冰阻力时程如图17（b）所示，取60 ～80 s 段计算破冰的平均阻力，该工况下船体平均阻力为75.56 N。

图17 船体阻力计算结果

图18 所示为不同螺旋桨转速下的流场模拟结果。从图中可以看出，由于冰层破碎后，碎冰大部分被挤压到两侧平整冰层下方，下潜到船体底部的海冰较少，因此破碎的海冰与螺旋桨之间不会频繁发生碰撞。

图18 不同螺旋桨转速下流场模拟结果

图19 所示为2 个螺旋桨所受的总推力及所受的力矩情况。从图中可以发现，该工况中3 个转速下的推力呈现线性增加趋势，且对应扭矩的增加也符合线性规律。

图19 螺旋桨所受推力及扭矩时程

图20 所示为尾部流场对船体结构的作用力以及计算得到的推力减额值。从图中可以看出，随着螺旋桨转速的增加，该工况中推力减额的变化情况基本呈线性增加趋势，与其推力的线性增加趋势一致。

图20 不同转速下的推力减额情况

将计算结果统计后列于表4 中，计算各个转速下的强制力，并采用浮冰工况类似的拟合方式获得自航时所需的螺旋桨转速（该工况下所需螺旋桨转速为501.8 r/min），计算航速分别为0.282 m/s 和0.188 m/s，而后将结果汇总于表5。

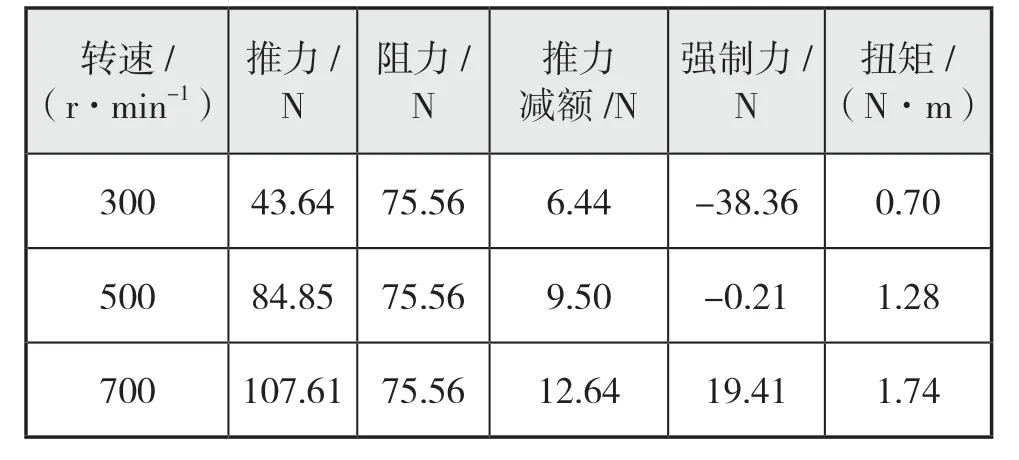
表4 层冰工况中不同螺旋桨转速的计算结果

表5 计算结果汇总表

3 结 语

由于冰区船舶的快速性需要同时考虑海冰和海水的耦合作用，目前尚未有采用冰-水-船三者耦合开展冰区船舶快速性预报的研究报道。本文采用海冰离散元方法和海水光滑粒子流体动力学方法建立了冰水耦合的DEM-SPH 模型，结合DEM-SPH 耦合方法的优势和特点，形成了冰区船舶快速性预报的方法流程，并将船体和螺旋桨视为刚体模型，形成了阻力-推力预报模型。文中采用DTMB 5415 船模模拟了船舶在浮冰区和层冰区的航行过程，分析了不同航速下船体阻力和螺旋桨推力，将尾部流场对船体的阻力增额作为推力减额值，拟合了船模强制力随螺旋桨转速的变化曲线，从而获得了船舶自航下的螺旋桨转速。基于上述模型分别针对浮冰区和层冰区进行了自航螺旋桨转速计算，所得计算结果具有一定合理性。由于目前未能开展相关模型试验研究，因此后期还需要进一步结合模型试验结果验证预报结果的准确性，并优化计算分析流程，从而使本模型可以为极地航行船舶的船机桨匹配工作提供计算参考。