930MPa级大直径高强冷滚压螺纹预应力钢筋S–N曲线研究

李宇欢 常好诵 傅彦青,3 任志宽 常海林

930MPa级大直径高强冷滚压螺纹预应力钢筋–曲线研究

李宇欢1,3常好诵1,2傅彦青1,2,3任志宽1,2常海林1,2

(1. 中冶检测认证有限公司，北京 100088；2. 中冶建筑研究总院有限公司，北京 100088；3. 西南交通大学土木工程学院，成都 610031)

考虑大直径钢筋横截面材料不均匀问题及钢筋螺纹根部应力集中，对930 MPa级的75 mm直径高强冷滚压螺纹预应力钢筋横截面不同位置材料开展了单轴拉伸及疲劳性能试验研究，并对全尺寸钢筋进行单轴拉伸有限元数值模拟，以分析螺纹根部应力集中，基于计算结果及疲劳试验数据，修正得到了适用于930 MPa级75 mm直径高强冷滚压螺纹预应力钢筋的曲线。结果表明：大直径高强冷滚压螺纹预应力钢筋单轴拉伸应力–应变曲线无屈服平台，930 MPa级的75 mm直径钢筋横截面材性存在显著差异；螺纹根部存在明显的应力集中，应力集中系数约为1.74；平均应力为700 MPa时，其疲劳性能与GB 50017—2017《钢结构设计标准》中考虑尺寸效应的Z11曲线接近。

冷滚压螺纹；大直径预应力钢筋；力学特性；应力集中；疲劳性能

0 引 言

大直径高强冷滚压螺纹预应力钢筋具有高强度、高疲劳性能、高尺寸精度、低松弛率、低张拉回缩等优良性能，广泛应用于大型水利工程、工业和民用建筑中的连续梁和大型框架结构，公路、铁路大中跨桥梁、核电站及地锚等工程，近年在我国重大跨海装配式桥梁工程中应用需求广泛。国内以往采用精轧螺纹钢筋（图1（a）），但受生产装备和轧制工艺的制约，其公称直径一般不超过50 mm，短预应力钢筋张拉后的预应力损失值高达50%，容易引起混凝土结构开裂，制约了其在桥梁工程中的推广和应用。而冷滚压螺纹钢筋（图1（b））利用冷滚压工艺成型，通过挤压使得钢筋表面组织致密，促使表面硬化，提高材料疲劳性能的同时加工长度不受长径比的限制[1-3]，钢筋直径可达75 mm以上，且规格较为灵活。同时，因其具有高效、节能、低耗成型工艺，且握裹力可靠、张拉后回缩值小等优点，在国际上已较广泛的采用。

图1 高强螺纹钢筋

目前，大直径高强冷滚压螺纹预应力钢筋在港珠澳大桥、南宁英华大桥、翔安大桥等重大工程中已得到应用[1,4]。林立华等对大直径高强冷滚压螺纹预应力钢筋的微观组织和力学性能展开研究，研究结果表明：钢筋横截面组织存在一定的不均匀性，调质热处理具有改进空间，改善调至工艺可提高钢筋的疲劳性能，并建议设计阶段的钢筋采用多折线模型进行计算[1]。文献[5-7]对大直径高强冷滚压螺纹预应力钢筋连接锚固体系、应力腐蚀断裂等方面进行了深入研究，研究结果表明：钢筋采用冷滚压连续全螺纹形式，具有工艺成熟、性能稳定的特点；配套锚具具有锚固可靠，组装件性能优良的特点；钢筋发生应力腐蚀后，裂纹扩展速度与其所受拉应力值高低关系不大，主裂纹位于螺纹与螺纹底部相交处。陈俊等[8]对大直径高强冷滚压螺纹预应力钢筋进行了张拉锚固损失、有效张拉力水平的研究，研究结果表明：钢筋的预应力损失明显低于传统螺纹钢筋，有效张拉力为传统螺纹钢筋的0.95～1.02倍。虽然有学者对大直径高强冷滚压螺纹预应力钢筋进行了深入研究，但目前尚存在不足：

1）钢筋疲劳性能的研究较少，螺纹根部存在很大的应力集中，提高了螺纹根部应力大小，缩短了钢筋的疲劳寿命。

2）对钢筋的使用缺少明确规定，钢筋作为预应力筋时，对钢筋的张拉力控制值缺少详细说明，过小的预应力将增大材料用量，过大的预应力则会降低钢筋的疲劳寿命，致使结构易发生疲劳破坏。

基于上述存在的不足，对930 MPa级的75 mm直径高强冷滚压螺纹预应力钢筋（以下简称“钢筋”）进行研究，分析了钢筋横截面距中心不同位置处材料的力学性能差异，得到了表层材料的应力–应变关系、延伸率、–曲线；随后考虑螺纹根部的应力集中，得到了适用于钢筋的–曲线，并将其与GB 50017—2017《钢结构设计标准》中规定的–曲线进行对比。

1 拉伸试验

1.1 试验概述

930 MPa级的75 mm直径高强冷滚压螺纹预应力钢筋的材料为42 CrMo，其化学成分及质量百分比见表1。

表1 直径75 mm高强冷滚压螺纹预应力钢筋化学成分

依据GB/T 228.1—2021《金属材料拉伸试验第1部分：室温试验方法》[9]中规定的尺寸大小，分别切取钢筋截面距中心不同位置处材料，加工成厚度为5 mm的标准拉伸试件。疲劳裂纹一般从材料的表面萌生，须重点关注表层材料的应力–应变关系，因此表层材料制成的标准试件（B5组）3个，芯部材料制成的标准试件（X5组）1个。本文采用MTS 322.31（250 kN）电液伺服疲劳试验机进行单轴拉伸试验。在试件的试验段中部安装引伸计。试件切取位置和尺寸如图2所示。试件的荷载、位移与应力–应变关系由测试系统自动记录。

1.2 试验结果及分析

试验加载到峰值后，试件发生颈缩，随荷载的继续增大，试件开始出现裂缝，随后发生断裂。断裂后的试件如图3所示，拉伸试验的应力–应变曲线如图4所示，试件试验结果及参数如表2所示。试验结果表明：钢筋材料没有明显的屈服平台；表层材料的强度值高于芯部材料的强度值；表层材料的屈服强度、极限强度满足GB/T 3077—2015《合金结构钢》[10]中的930 MPa和1 080 MPa 的要求，而试件B5-2的断面收缩率为11%，略低于规定的12%；芯部材料的屈服强度、极限强度均低于规定强度，断面收缩率为16%，高于规定要求。试件个数有限，钢筋的生产工艺、试件加工等过程存在一定的不确定因素，使试验存在一定的离散性。

图2 试件切取位置和尺寸mm

图3 拉断的试件

表2 材料力学性能参数

图4 应力–应变曲线

1.3 本构模型的建立及验证

文献[11-14]针对无明显屈服平台钢材，提出了全局的应力–应变模型，即Rasmussen模型，表达式如下：

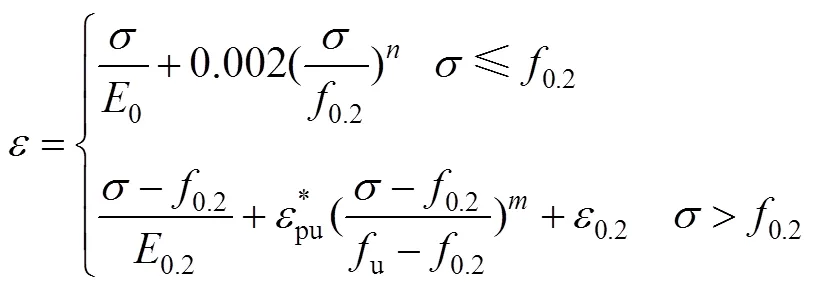
其中= ln20/ln(0.2/0.01)

0.2=0/(1+0.0020/0.2)

0.2=0.2/0+0.002

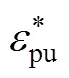
式中：u为极限强度所对应的应变。

将试验得到的应力应变曲线采用ture=ln（1+nom）和ture=ln（1+nom）方式对试验得到的应力、应变进行变换，得到真实应变ture和真实应力ture，与Rasmussen模型拟合得到的应力–应变曲线进行对比，如图5所示。

对比结果表明：表层材料初始弹性模量的均值为210 000 MPa，屈服时弹性模量降低到13 515～23 650 MPa；采用Rasmussen模型表达式能够很好的描述钢筋表层材料的应力–应变关系。表层材料的值为20.33～ 40.28，均值为30，大于芯部材料的值，表层材料的值为2.21～3.432，均值为2.736。当缺少试验数据时，可近似取为20～40，为2～3。

2 疲劳试验

2.1 试验概述

疲劳试件的尺寸与拉伸试件尺寸相同（图2），表层材料制成7个试件（PB5组），芯部材料制成3个试件（PX5组）。疲劳试验采用长春仟邦生产的型号为QBG300的高频疲劳试验机（图6），采取拉–拉循环加载方式，加载频率为75～77 Hz。

QBG300高频疲劳试验机利用机械系统共振原理工作，当裂纹扩展到一定长度时，试件刚度急剧下降，振动频率下降低于设定的阈值，试验机将会停机，可在试件表面观察到疲劳裂纹，此时视为试件破坏。设置最大循环次数200万次，当循环次数达到200万次试件仍未开裂，试验机将会自动停机。

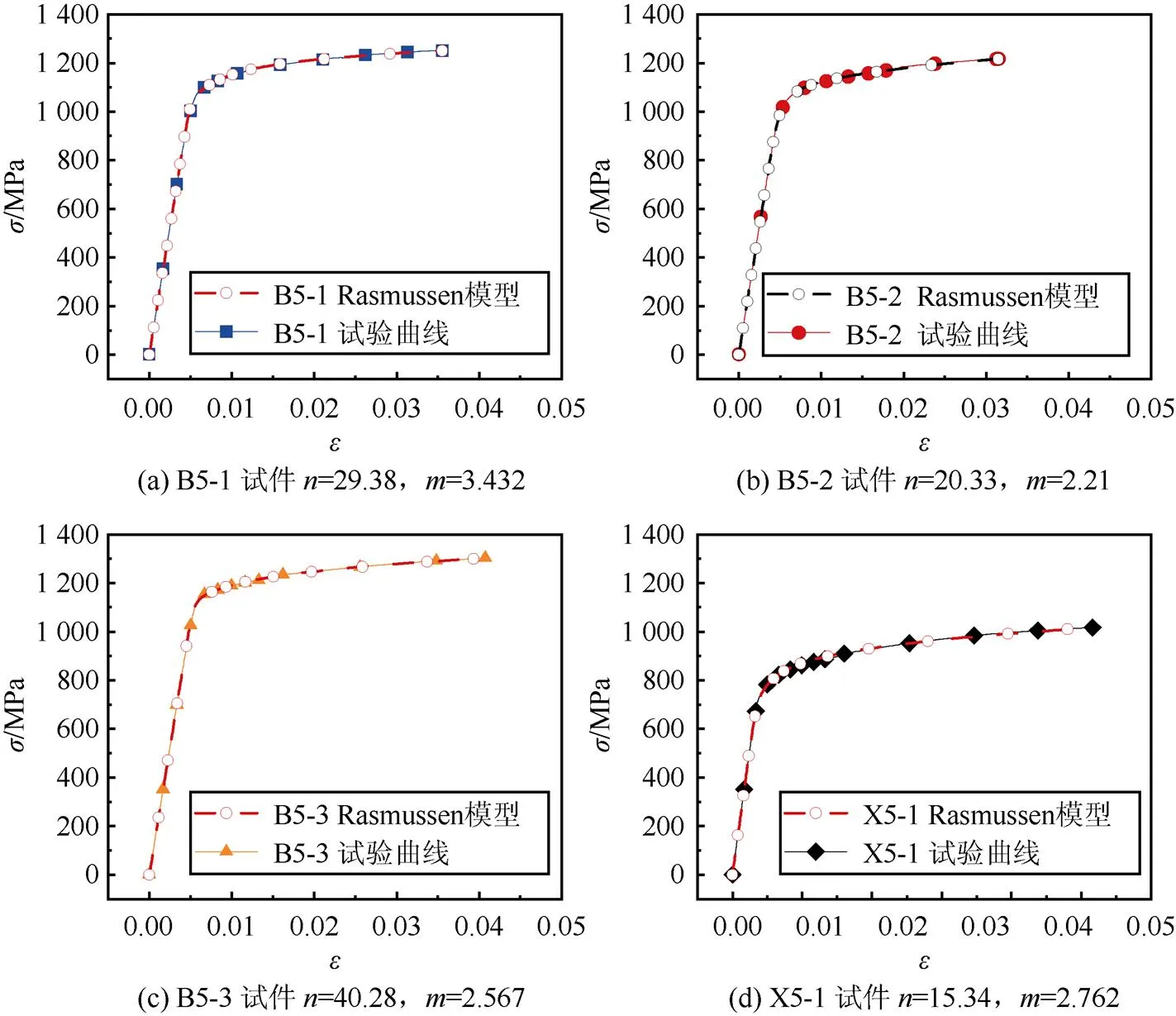
图5 试验与本构模型对比

图6 QBG300高频试验机

Fig.6 QBG300 high-frequency testing machine

图7 试件疲劳裂纹位置

2.2 试验结果及数据处理

钢筋主要用作预应力筋，实际服役时处于预先张拉状态，因此本试验试件平均应力控制为500 MPa。具体加载方案及试验结果如表3所示。拉伸试验已经获得钢筋芯部材料的屈服强度大约为800 MPa，无法将芯部试件的荷载加载到与表层试件一样的荷载水平，因此将芯部试件加载的应力幅控制为300，270，250 MPa三个应力等级。

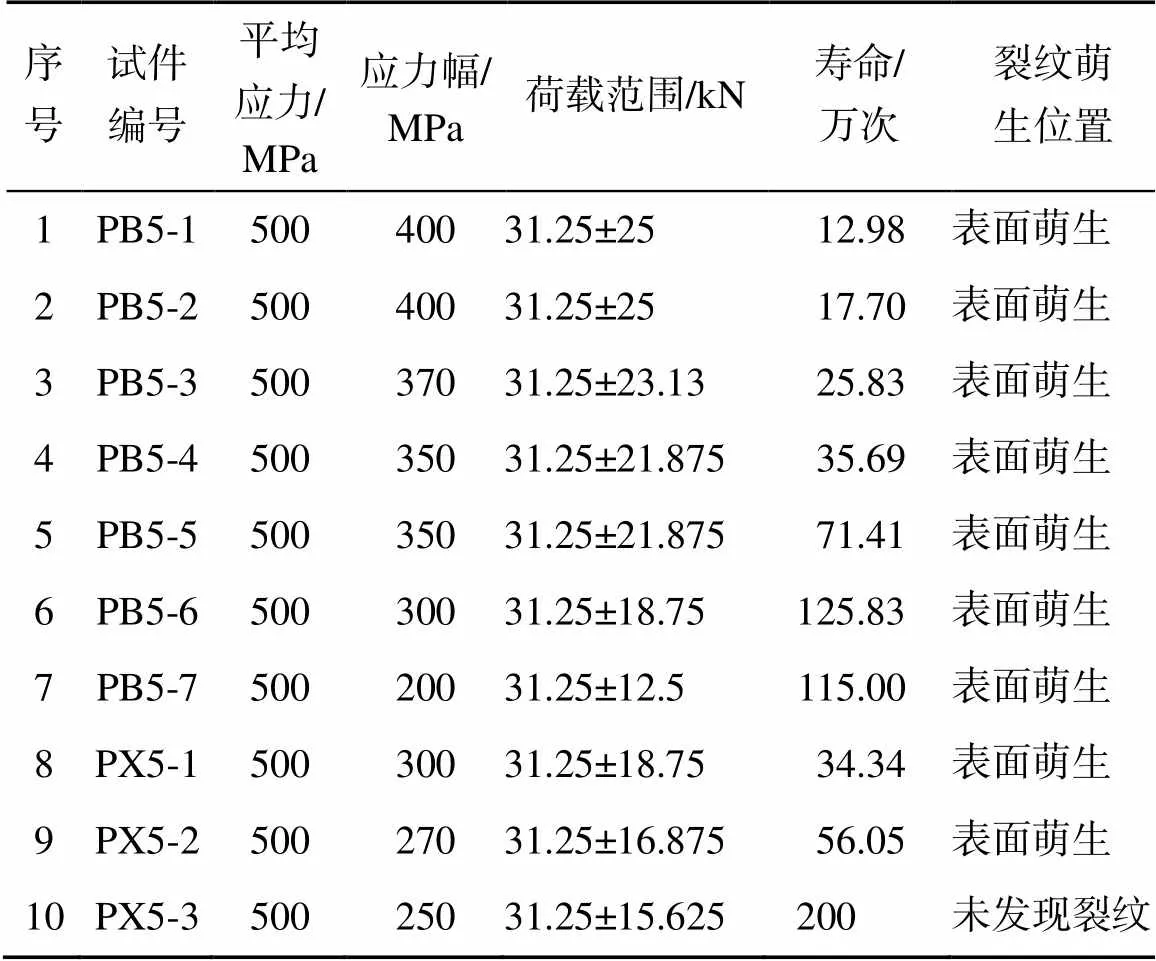
表3 疲劳试验加载制度及试验结果

由图7及表3中的裂纹萌生位置可以看出，试件裂纹萌生都是发生在试件表面，无内部萌生的情况。疲劳试验结果表明：芯部材料的疲劳性能低于表层材料的疲劳性能，这主要是钢筋表面残余压缩应力提升了疲劳性能。钢筋表面的残余压缩应力来源大致有两个方面：

1）滚压成形。采用滚轮施压，螺纹根部金属被压实，表层材料发生塑性变形形成螺纹，并在表层存在残余压应力。

2）缺口处发生不均匀的塑性变形。螺纹根部由于应力集中的存在，使其峰值应力max超过屈服强度并产生局部的塑性变形区。由于塑性变形，使max小于t，t为应力集中系数。在螺纹根部塑性区的材料被拉长，产生了永久的塑性变形。外荷载去掉后，由于周围材料仍处于弹性状态，将趋向回到初始的变形，这样周围材料将对塑性区产生约束作用。塑性区将受到压缩，不再是无应力状态，进而在螺纹根部引入了残余压应力。

根据GB/T 24176—2009《金属材料疲劳试验数据统计方案与分析方法》[15]对表层材料的疲劳试验结果进行统计分析。疲劳寿命和循环应力幅之间的关系可利用线性的数学模型表示：

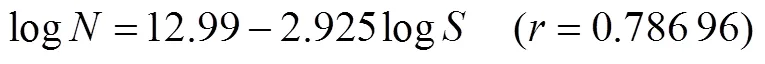
式中：为相关系数。

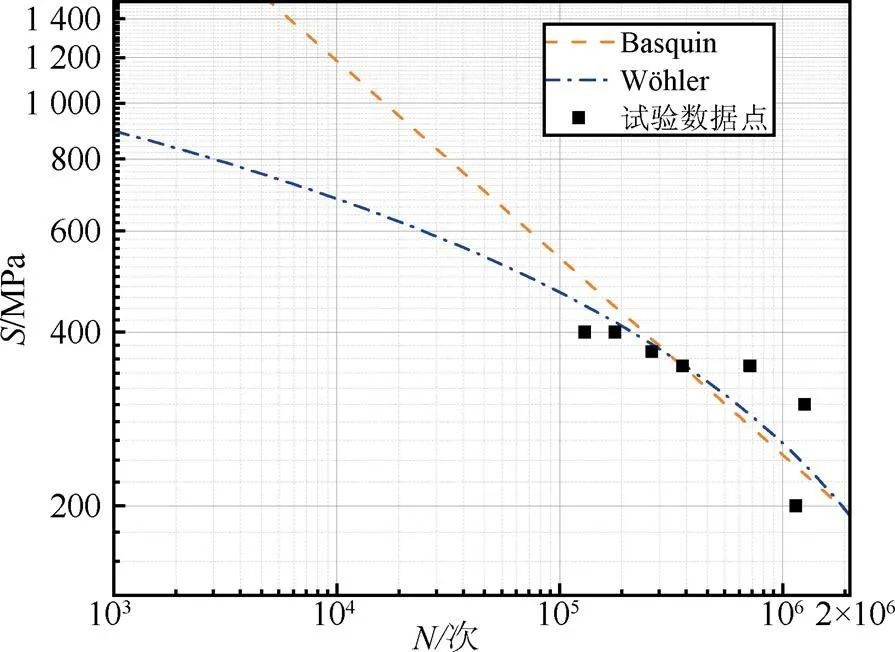
图8 统计曲线对比

由图8可以看出，两种方法统计得到的曲线总体走势相似，随着应力幅的降低，疲劳寿命逐渐增大。此外，由于疲劳试验具有很大离散性，且疲劳寿命越高，离散性越大，本文受条件限制，仅在同一应力水平下对1～2个试件进行疲劳试验。

3 钢筋S–N曲线确定

3.1 应力集中计算

钢筋螺纹附近处的受力情况比较复杂，主要表现为钢筋外径不但环绕着螺纹，而且这些螺纹沿着钢筋轴线方向有一定升角，这个升角被称为“导程角”。1994年，Zhao指出，在导程角较小的情况下，应力沿螺纹齿的分布几乎不受导程角影响，应力相差仅1%左右，因此对螺纹的研究可忽略导程角影响[16]。本文基于此假设建立有限元模型，同时为消除缺口处的应力受相邻缺口周围应力的影响，建立了5个螺纹的二维简化模型，模型的几何尺寸及有限元模型如图9所示。

图9 几何尺寸及有限元模型

由图4可以看出，不同位置处的材料差异主要表现在800 MPa后，钢筋服役及试验时平均应力未超过材料屈服强度且低于800 MPa，仍处于弹性阶段，该阶段不同位置处的材料无明显差异。此外，疲劳裂纹起始于构件表面，表面螺纹处的应力集中提高了螺纹处的应力，因此本文忽略不同位置处材料差异对疲劳性能造成的影响，按同质、均匀材料建立有限元模型，分别采用拟合得到的表面材料的Rasmussen本构模型和线弹性本构模型，对比计算螺纹根部的应力集中系数，同时对螺纹根部网格尺寸进行细化。模型一端设定方向（拉伸方向）的对称约束，另一端施加拉应力。图10显示了采用不同本构模型计算螺纹根部应力集中系数的计算结果。计算结果表明，在平均拉应力低于570 MPa时，两种本构模型对应力集中系数的计算结果相同，当平均拉应力高于570 MPa，采用Rasmussen模型计算的应力集中系数偏小。这是因为当平均拉应力超过570 MPa，螺纹根部的最大应力虽然没有达到屈服，但已超过材料的比例极限，材料的应力–应变关系已不再是线弹性关系，此时若采用线弹性本构模型将得到偏大的结果。

图10 应力集中系数计算结果

3.2 影响系数的确定

3.2.1 缺口疲劳系数

应力集中通常会降低疲劳强度，抗疲劳设计时必须考虑缺口处的应力集中。理论应力集中系数是在弹性范围内由弹性理论计算得来，而实际钢筋具有一定塑性，从而使螺纹根部的应力重新分布，这样采用理论应力集中系数来描述应力集中对疲劳强度的影响就会产生较大的偏差，所以在工程中常用缺口疲劳系数f来表示[17-18]。不同学者以各种假设为基础，通过大量的试验研究得到了一些方法和经验估算式来表示缺口疲劳系数与应力集中系数间的关系，例如查表法、敏感系数法[19-20]、应力梯度法、断裂力学法[21]等。但目前来看，敏感系数法是比较简便和实用的方法[17,22]。

敏感系数法是引入的一个系数来描述f与t之间的差别，它们之间的关系式为：

式中：为疲劳缺口敏感系数。

Peterson提出了一种描述应力集中系数与疲劳缺口敏感系数间的关系式[17,22]，即：

式中：为缺口半径，为材料常数，可查表4确定。

表4 Peterson公式中材料常数α

3.2.2 尺寸系数

1994年，Zhao[16]指出，在螺纹导程角较小情况下，应力沿螺纹齿的分布几乎不受螺纹导程角影响，因此钢筋在不考虑导程角影响的情况下，任意横截面均为圆形截面。Shigley和Mitchell于1983年给出了圆形截面尺寸系数表达式[23]：

钢筋直径为75 mm，带入式（8）可得钢筋尺寸系数s=0.782 2。

3.2.3 表面系数

1986—1987年，郑州机械研究所用8种材料5种不同终加工方法对表面加工系数进行了一系列研究，得到表面加工系数曲线图（图11）。本文钢筋生产工艺为冷滚压，属于锻造工艺，故1取0.55。

本文不考虑钢筋在海水、酸碱溶液等腐蚀介质服役的情况，因此并未考虑腐蚀系数2的影响，将此系数取为1。

图11 表面加工系数曲线[23]

表面强化系数可通过查看《抗疲劳设计手册》获得，该手册给出了42 CrMo钢滚压前后的疲劳极限（表5），参考表5，以内插方式得到钢筋的表面强化系数3=1.25。

表5 42 CrMo钢滚压前后疲劳极限[23]

3.3 S-N曲线修正

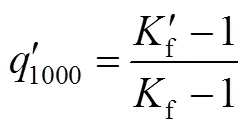
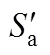
图12 Heywood模型

Fig.12 Heywood model

图13 钢、铝、镁在不同强度下的q'1000[23]

图8可以看出在寿命较高时采用Basquin表达式更加安全，寿命较低时采用Wöhler表达式更加安全，因此本文在=1 000时以Wöhler表达式计算其应力幅，在=2×106时以Basquin表达式计算其应力幅，如图14所示。连接两点得到的直线包络了Basquin表达式和Wöhler表达式的两条曲线，从而保证钢筋具有足够的安全冗余度。本文根据Heywood模型对材料曲线进行修正，修正后得到适用于钢筋在平均应力500 MPa时的曲线：

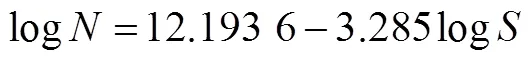
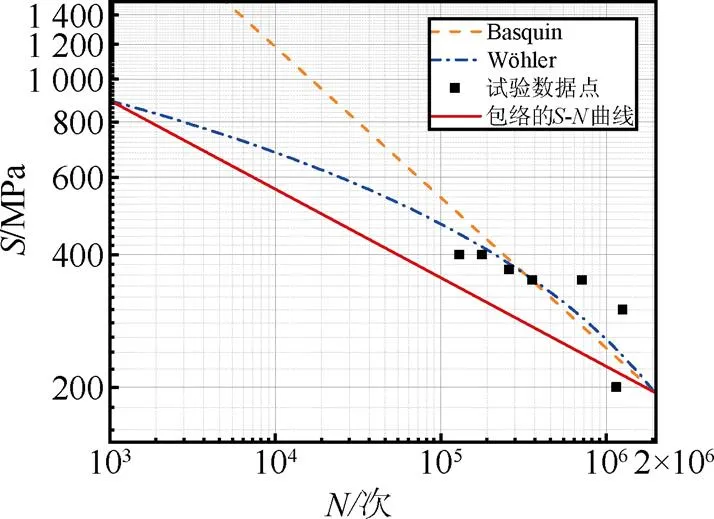
图14 包络两种表达式的S–N曲线

4 钢筋张拉应力值确定

平均应力对疲劳寿命的影响，不同的学者提出了不同的表达式，比较成熟的有Gerber模型、Goodman模型、Soderberg模型等。其中，Soberberg模型过于保守，Gerber模型偏于危险，Goodman模型偏于保守。因此Goodman模型在工程实际中常用。带入不同的m，即可得到不同平均应力下的曲线，Goodman模型表达式如下：

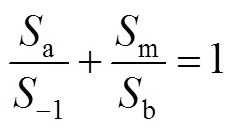
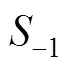
我国GB 50017—2017《钢结构设计标准》中按连接类别的不同，划分了14条应用于疲劳计算的曲线。其中Z11曲线适用于受拉高强螺栓的螺纹母材，与钢筋螺纹类似，因此将不同平均应力下的曲线与Z11曲线绘制在同一坐标系下进行对比，如图15所示。当螺栓直径大于30 mm时，须通过折减系数t修正应力幅以考虑尺寸效应，其计算式如下：

式中：为螺栓的直径，mm。

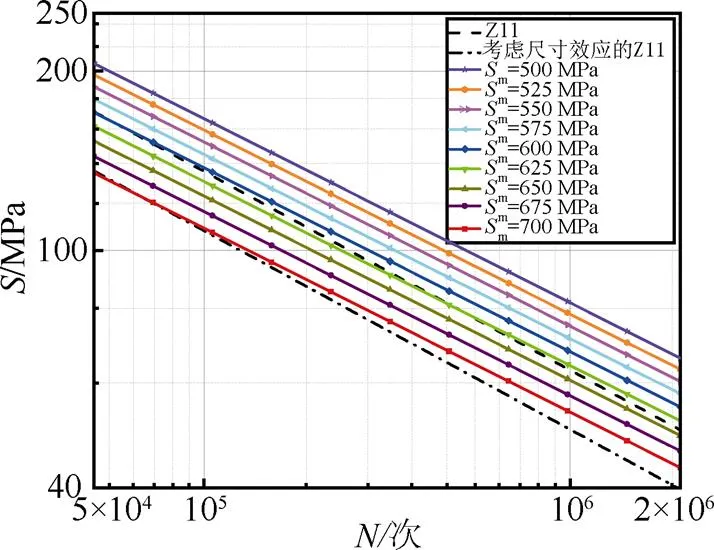
图15 不同平均应力下钢筋S–N曲线与Z11连接方式S–N曲线对比

钢筋直径为75 mm，大于30 mm，经计算得到折减系数t=0.795 27，折减后Z11曲线为：

Log=11.397 9 – 3log（13）

图15表明：随着平均应力的增大，钢筋的疲劳性能逐渐下降，曲线的负斜率在3～4，这与GB 50017—2017《钢结构设计标准》所规定的斜率（3或4）相近。钢筋的平均应力为700 MPa时，其疲劳性能与考虑尺寸效应的Z11曲线所代表的疲劳性能接近，尤其在寿命较低时（10万次以内），两条曲线近似重合。

5 结束语

1）930 MPa级的大直径高强冷滚压螺纹预应力钢筋横截面材料存在不均匀性。表层材料经滚压后其极限强度、屈服强度均高于芯部材料；钢筋材料无明显屈服平台，采用Rasmussen模型能够很好地描述材料的应力–应变关系。

2）930 MPa级的大直径高强冷滚压螺纹预应力钢筋表层材料经滚压处理后，表层产生残余压应力，其疲劳性能明显优于芯部材料；依据GB/T 24176—2009《金属材料疲劳试验数据统计方案与分析方法》对试验结果进行统计分析，分析结果表明应力幅与疲劳寿命间具有线性关系。

3）在平均拉应力低于570 MPa时，采用线弹性模型或Rasmussen模型均可准确求得螺纹根部的应力集中系数；当平均应力超过570 MPa时，因螺纹根部局部区域材料超过比例极限，采用线弹性模型求得的应力集中系数偏大，应采用Rasmussen本构模型进行求解。

4）采用Heywood模型对表层材料的曲线进行修正，得到适用于930 MPa级的大直径高强冷滚压螺纹预应力钢筋的曲线；根据Goodman模型得到钢筋在不同平均应力下的曲线；平均应力为700 MPa时的曲线与GB 50017—2017中考虑尺寸效应的Z11曲线接近。

[1] 林立华, 傅彦青, 常海林, 等. 翔安大桥装配式墩台冷滚压螺纹预应力钢筋微观组织与力学性能研究[J]. 工业建筑, 2023, 53(08): 199–205.

[2] 吴上生, 孙韩磊, 杨琪. 基于冷滚压工艺的谐波减速器柔轮疲劳寿命分析[J]. 机械传动, 2019 ,43(01): 131–135+164.

[3] 袁武华, 邓建伟, 申庆援, 等. 圆角滚压对螺栓残余应力分布及疲劳寿命的影响[J]. 锻压技术, 2023, 48(01): 108–114.

[4] 崔怀俊, 盛剑. 大直径高强螺纹钢筋在港珠澳大桥预制墩台中的应用[J]. 中国港湾建设, 2017, 37(06): 77–80.

[5] 朱万旭, 李明霞, 付委. 港珠澳大桥桥墩拼接用大直径螺纹钢筋应力腐蚀断裂试验研究[J]. 公路, 2020, 65(10): 112–117.

[6] 朱万旭, 覃荷瑛, 甘国荣, 等. 港珠澳大桥节段预制桥墩高强钢筋联接锚固体系的关键技术研究[J]. 铁道学报, 2017, 39(05): 118–124.

[7] 朱万旭, 张贺丽, 甘国荣, 等. 港珠澳大桥预制拼装桥墩预应力高强螺纹钢筋锚固体系试验研究[J]. 施工技术, 2017, 46(16): 101–105.

[8] 陈俊, 李明, 肖祥淋, 等. 连续梁大直径预应力钢棒试验研究[J]. 中国铁路, 2016(01): 61–66.

[9] 全国钢标准化技术委员会. 金属材料拉伸试验第1部分: 室温试验方法: GB/T 228.1—2021[S]. 北京: 中国标准出版社, 2021.

[10] 全国钢标准化技术委员会. 合金结构钢: GB/T 3077—2015[S].北京: 中国标准出版社, 2015.

[11] HILL H N. Determination of stress-strain relations from ‘offset’ yield strength values[J]. Pediatrics, 1994, 6(1): 93–97.

[12] MIRAMBELL E, REAL E. On the calculation of deflections in structural stainless steel beams: an experimental and numerical investigation[J]. Journal of Constructional Steel Research, 2000, 54(1): 109–133.

[13] RASMUSSEN K J R. Reply to: discussion of full-range stress-strain curves for stainless steel alloys[J]. Journal of stainless steel alloys[J]. Journal of Constructional Steel Research, 2003, 59(10): 1325–1326.

[14] 饶兰, 岳清瑞, 郑云, 等. 高强耐蚀钢材料力学特性试验研究[J]. 建筑结构学报, 2020, 41(5): 147–156.

[15] 全国钢标准化技术委员会. 金属材料疲劳试验数据统计方案与分析方法: GB/T 24176—2009[S]. 北京: 中国标准出版社, 2009.

[16] ZHAO H. Analysis of the load distribution in a bilt-nut connector [J]. Computer and Structures, 1994, 53: 1465–1472.

[17] 李舜酩. 机械疲劳与可靠性设计[M]. 北京: 科学出版社, 2006.

[18] 金丹, 田大将, 李江华, 等. 缺口半径对疲劳寿命影响的有限元分析[J]. 航空动力学报, 2015, 30(07): 1618–1623.

[19] NEUBER, H. Theory of stress concentration for shear-strained prismatical bodies with arbitrary nonlinear stress-strain law[J]. Journal of Applied Mechanics, 1961, 28(4): 544–550.

[20] NEUBER H. Theory of notch stresses: principles for exact calculation of strength with reference to structural form and material[M]. Berlin: Springer Publishers, 1958.

[21] YU M T, DUQUESNAY D L, TOPPER T H. Notch fatigue behavior of SAE1045 steel[J]. International Journal of Fatigue, 1988, 10(2): 109–116.

[22] 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003.

[23] 赵少汴. 抗疲劳设计手册[M]. 北京: 机械工业出版社, 2015.

Research on-Curves of 930MPa Large-Diameter High-Strength Cold-Rolled Threaded Prestressed Steel Rebars

LI Yuhuan1,3CHANG Haosong1,2FU Yanqing1,2,3REN Zhikuan1,2CHANG Hailin1,2

(1. Inspection and Certification Co., Ltd., MCC, Beijing 100088, China; 2. Central Research Institute of Building and Construction Co., Ltd., MCC Group, Beijing 100088, China; 3. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

Considering the problem of uneven cross-section of material of large-diameter steel rebars and the stress concentration at the root of thread rebars, the paper carried out an experimental study of uniaxial tensile and fatigue properties of materials at different positions of the cross-section of 930 MPa grade 75 mm diameter high-strength cold-rolled threaded prestressed steel rebars, and carried out a finite element numerical simulation of full-size steel rebars under uniaxial tensile to analyze the stress concentration at the thread root. The results showed that there was no yield platform in the stress-strain curves of large-diameter high-strength cold-rolled threaded prestressed steel rebars under uniaxial tensile, and there were significant differences in the cross-sectional material properties of the 930 MPa grade 75 mm diameter steel rebars. There was an obvious stress concentration at the thread root, and the stress concentration coefficient was about 1.74, and the fatigue properties was very close to the Z11 curve considering the size effect in the(GB 50017—2017) when the average stress was 700 MPa.

cold-rolled threads; large-diameter prestressed steel rebars; mechanical properties; stress concentration; fatigue properties

李宇欢, 常好诵, 傅彦青, 等. 930 MPa级大直径高强冷滚压螺纹预应力钢筋–曲线研究[J]. 工业建筑, 2024, 54(1): 115-122. LI Y H, CHANG H S, FU Y Q, et al. Research on-Curves of 930 MPa Large-Diameter High-Strength Cold-Rolled Threaded Prestressed Steel Rebars[J]. Industrial Construction, 2024, 54(1): 115-122 (in Chinese).

10.3724/j.gyjzG23111502

*国家自然科学基金项目（52078508）；国家重点研发计划课题（2022YFB3706403）。

李宇欢，工程硕士，助理工程师，主要从事高性能钢材疲劳性能研究，804226768@qq.com。

傅彦青，191607093@qq.com。

2023-11-15