超高层建筑动力特性监测方法研究进展*

伍永靖邦 金 楠 施钟淇 岳清瑞 钟儒勉

超高层建筑动力特性监测方法研究进展*

伍永靖邦1,2,3金 楠1,2,3施钟淇1,2,3岳清瑞1,2,3钟儒勉1,2,3

(1. 深圳市城市公共安全技术研究院有限公司，广东深圳 518046；2. 城市安全风险监测预警应急管理部重点实验室，广东深圳 518038；3. 城市安全发展科技研究院（深圳），广东深圳 518046)

随着城市化进程的加速，我国超高层建筑数量急剧增加，然而这些建筑在运营和维护方面存在的问题也逐渐凸显。超高层建筑的服役安全问题引起了学者们的广泛关注。通过对超高层建筑动力特性参数识别的理论方法和实践应用的总结和分析，对以时域、频域、时频域及新型模态识别方法为代表的超高层建筑结构监测技术特点进行了归纳，然后对比了各类监测技术和系统的优势和局限性，并总结了当前超高层监测技术存在的主要问题，探讨了监测技术的发展趋势。最后对动力特性识别方法在超高层监测中的应用进行了梳理，以期为提高超高层建筑的动力特性识别和监测的准确性、有效性和可靠性提供参考依据，为提高我国超高层建筑的安全运营和维护水平提供借鉴。

超高层建筑；动力特性；参数识别；健康监测；服役安全

随着社会经济的发展和城镇化进程的加速，我国的超高层建筑数量急剧增加。截至2023年7月，我国拥有150 m以上的超高层建筑共计3 090栋，300 m以上的超高层建筑达108栋，均位居世界第一。[1]然而，随着建筑高度的不断提高和结构形式的日益复杂，超高层建筑在运营和维护等方面存在的问题也逐渐凸显。美国纽约千禧大厦于2009年竣工后不久出现异常振动，至今仍面临着沉降和倾斜的困扰。2021年5月18日，深圳赛格大厦的异常振动事件引起了社会的广泛关注。2023年5月深圳百富兴大厦发生的异响和振动事件受到了各界重视。超高层建筑运营中的异常现象屡见不鲜，超高层建筑的服役安全问题得到了高度重视，同时也成为了学者们关注的焦点。

我国超高层建筑整体表现为体量大、种类多、使用寿命长、服役环境复杂。美国纽约千禧大厦因建筑结构设计、地基沉降及外部环境影响等产生倾斜和振动；深圳赛格大厦异常振动是由桅杆风致涡激共振和大厦桅杆动力特性改变的耦合效应所引起；深圳百富兴大厦长期以来受上部结构荷载作用和周边施工扰动，造成承载力下降，产生不均匀沉降，导致受损柱承担的轴向力达极限值，从而发生压屈破坏。各类超高层建筑异常振动事件的发生表明，有必要对超高层建筑动力特性采取必要的长期监测。

鉴于此，将对目前超高层建筑动力特性参数识别的理论方法和实践应用进行总结，分析各类监测技术与系统的优势和局限性，总结当前超高层监测技术存在的主要问题和发展趋势，为进一步提高超高层建筑的监测水平提供有益的帮助。

1 超高层建筑动力特性参数识别方法

通过对近二十年来以“结构健康监测”为关键词的论文进行了检索，结果表明：损伤识别、动力特性、模态参数等关键词为高频词（图1），准确地识别和监测这些结构模态参数成为近年来的热门研究方向，也为超高层建筑结构损伤识别、健康监测与安全评价提供了重要的参考依据。[2-4]

针对超高层建筑的动力特性识别和监测问题，国内外专家学者已进行了大量的研究[5-6]，并提出和发展了多种模态参数识别方法。当结构受到损伤时，其动力特性会发生变化。[7]监测模态参数的变化为结构健康监测提供了重要参考，对结构的安全运行和维持结构的使用性能具有重大意义。大型工程结构的动力学参数识别理论和方法已逐渐得到广泛应用，这些方法主要包括时域、频域和时频域方法。[8]

1.1 频域识别方法

频域识别方法通过傅里叶变换从时域信号中提取频域信号，进而对结构的频域响应信号进行分析和处理，得到结构的振动特性参数。基于振动进行损伤检测的频域法主要包括[9]、复模态指示函数法[10]和最小二乘复频域法[11]。

图1 近二十年以结构健康监测为主题的论文突现关键词

峰值拾取法（PP）是最经典也是最简单的结构频率识别方法。PP假设结构阻尼较小、模态易分离，可从结构的频谱响应中识别环境激励下结构的频率，然而当结构复杂或模态间隔紧密时，该方法对频率的识别精度会受到影响，尤其对于高阶频率的识别影响较大。为了突破这一限制，学者提出了频域分解法（FDD）[12]。FDD作为PP的延伸，解决了PP无法识别密集模态的问题，其基本原理为利用输出响应的功率谱密度矩阵奇异值分解的峰值来识别固有频率和振型。FDD具有一定的抗噪声干扰和密集模态分辨能力，但无法识别阻尼比。因此，学者们对FDD进行了改进，如Pioldi等提出的增强FDD技术[13-14]，可对地震激励下的结构模态特性进行有效监测。为更适用于高层建筑等复杂结构的模态分析，Kim等提出了模态分析过程中三种测量分析条件的下界和上界准则作为增强FDD方法的最小条件[15]，通过对某35层建筑的结构响应验证，该方法得到了可靠的模型参数结果。通过现有的PP或FDD技术得到的频率和振型具有较高识别精度，然而，阻尼比的识别仍然是一个待解决的问题，这两类方法用来计算阻尼仍然存在一定偏差。[16]

模态指示函数法（CMIF）也可以视为PP法的延伸方法，CMIF通过对每条谱线上的正常频响矩阵进行奇异值分解来计算得到结构的频率、振型和模态参和向量等参数。CMIF在很大程度上突破了PP无法识别紧密间隔模态的瓶颈，可较为精准识别复杂结构的频率和相应振型，但与PP、FDD技术在阻尼比估计上存在同样的限制。[17]

最小二乘复频域法（LSCF）是一种快速且准确的频域模态估计方法。LSCF基于振动响应的功率谱，将系统的传递函数转换为多项式表达式，并利用最小二乘估计求解系数矩阵来求解模态参数。LSCF适用于大阻尼和密集模态情况，具有较快的识别速度。为了进一步提高LSCF的识别精度和抗干扰能力，多参考LSCF[18]被提出，该法可提高模态识别处理时间和精度，特别对阻尼估计准确性有极大提高。[19-20]

频域法计算快速，不同的频域模态识别方法在针对某些特定情况下的结构具有较高识别精度，但传统的频域法在分析非线性和非平稳信号时的精度可靠性较低，在低频范围内或合并模态数量较少的分辨率时，频域法所识别出的模态参数效果也较差。[21]此外，非参数频域法估计的阻尼比并不准确。[22]

1.2 时域识别方法

时域法通过结构的时程响应得到结构的振动特性，可用于反映结构的瞬态响应和非线性响应等动态特性，对于处于非稳态信号的结构分析具有一定的适用性。用于结构健康监测的时域法分为三大类：自然激励法[23]、自回归移动平均线法[24]和随机子空间法[25]。

自然激励法（NExT）是最早的模态分析方法之一。NExT利用平稳激励下结构两点之间的互相关函数来代替结构的脉冲响应函数，具有一定的抗干扰能力，但在实际应用中仍存在计算成本较高、精度有限等问题。因此NExT通常与特征系统实现算法（ERA）[26]结合来提取模态参数，如NExT-ERA[27]、ERA-NExT-AVG[28]、VFRF-ERA[29]等改进的算法被提出。除ERA法外，NExT与扩展Ibrahim时域法[30]、多参考复指数[31]等任何多输入多输出时域算法相结合都适用于紧密间隔甚至重复模态的复杂结构[32]，然而与SSI和FDD算法相比，NExT所获得的阻尼比结果的准确性较低。

自回归移动平均线法（ARMA）是一种基于自回归模型的时间序列分析方法，其中自回归部分旨在对线性函数时间历史进行建模，移动平均部分用于确定时间序列的移动平均。ARMA模型是受白噪声激励的线性非时变系统的广义模型，假定被识别系统的输出响应信号是平稳的。ARMA在土木工程结构健康监测中的应用广泛，为识别不同形式的损伤特征，ARMA存在大量的改进方法，如ARMAV用于识别结构固有频率的变化[33]，TV-ARMAV用于识别结构的所有模态参数[34]，TARMA用于识别固有频率[35]等。ARMA获取模态参数的鲁棒性强于其他时域法，但在实际应用中存在高计算时间的限制，且阻尼比的计算误差较大。

随机子空间法（SSI）是一种基于子空间分解的信号处理方法。土木工程领域所使用的SSI主要包括数据驱动SSI和协方差SSI两类，[36]协方差驱动SSI在识别精度和速度上均优于数据驱动SSI。SSI被广泛用于结构损伤和故障的检测，具有计算效率高、对噪声和干扰的抗干扰能力强等优点，较于NExT和ARMA所估计阻尼比的误差更小。[37]然而在实际应用中，SSI可能会产生虚假模态和真实模态遗漏等问题，因此须要进一步提高模态识别的准确性和效率。许多学者为提高SSI法模态识别的准确性和效率，提出了大量改进方法，包括基于蒙特卡洛稳定图的SSI[38-39]、针对耦合时变系统的短时SSI[40]、双折叠稳定图的改进SSI[41]等。

相较于频域分析，时域分析方法更适合于结构的连续监测，特别是当复杂高层结构存在大量模态或大频率范围时，时域方法提取的信息比频域方法更完整，但通常计算效率较低。

1.3 时频域识别方法

时域和频域识别方法通常要求环境激励是平稳白噪声，但由于建筑环境的复杂性，很难保证环境激励总是满足这一要求。为了解决这个问题，学者们提出了以小波变换[42]和希尔伯特黄变换[43]为代表的时频分析方法。时频法兼有时域法和频域法的优点，可运用于飓风和地震等极端灾害情况下高层建筑结构模态识别。[44]

小波变换直接根据频率对信号进行分解，并在时域中将其表示为频域分布状态，同时保留了信号的时间和频率信息。小波变换理论定义明确，但信号干扰、边界失真和能量耗散等限制了其在大数据分析中的应用。[45]希尔伯特黄变换是一种处理非线性非平稳数据的经验性方法，由经验模态分解和希尔伯特变换组成，其中经验模态分解可将任何复杂的数据集分解为有限的数据集，该方法效率高、自适应性强，适用于处理大规模数据。[46-47]

时频分析方法的信号分辨率通常低于传统的时域和频域分析方法，因此可能会出现信号混叠或漏失的情况，且时频分析方法的分析结果受到分析窗口的选择和参数设置的影响较大，计算复杂度较高，这会对结果的准确性、可靠性和时效性产生一定影响。因此在实际应用中，时频分析方法须要在选择分析方法、参数设置和结果解释等方面进行仔细考虑和评估。

1.4 新型模态识别方法

近年来，以数据驱动为核心的机器学习和深度学习成为结构健康监测热门研究方向（图2）。Rafiei等提出了一种基于无监督机器学习的高层建筑结构健康监测方法，该方法通过提取不同楼层传感器所记录的频域隐藏特征来对整体结构健康状况进行评估，并在38层钢筋混凝土建筑结构的缩尺模型上验证了所提出的方法。[48]Zhou等提出了一种基于极致梯度提升分类模型的SSI法，通过5自由度模型的数值模拟研究和195 m高建筑物的现场测量，验证了所提方法的准确性和有效性，并揭示了该建筑的固有频率和阻尼比的概率分布特征。[49]Georgioudakis等使用不同机器学习算法对多层剪力墙结构的动力响应进行了评估，结果表明基于类别增强的机器学习算法可以成功地预测响应。[50]但上述结果成立的前提为建筑结构的刚度和质量沿高度保持不变。各类研究表明模态识别的准确性在很大程度上取决于结构本身，以及传感器的位置和环境，同时机器学习算法的准确性依赖于专家对监测对象已有数据的特征选择。

图2 近二十年以结构健康监测为主题的论文突现关键词

贝叶斯方法[51]在模态参数识别领域备受关注，贝叶斯方法是一种基于概率统计分析原理的机器学习优化方法，将模态参数识别问题转优化问题，从而计算出模态参数的后验概率分布，并通过最大化后验概率来确定最优的模态参数估计值。贝叶斯方法的优势在于对模型参数的不确定性进行量化和分析，提供了更加严格的方法来评估模态参数识别的可靠性和准确性。贝叶斯方法经过改进已逐渐应用于大尺度结构的模态参数识别。[52-54]贝叶斯方法为实际工程的模态识别提供了重要应用价值，但该法仍受先验数据、识别精度与建模误差等限制，这些问题须要在未来投入大量的研究工作。[55]深度学习可与贝叶斯方法结合以降低计算的复杂性。[56-57]

深度学习较于机器学习具有更强的特征学习能力，卷积神经网络（CNN）被广泛应用于振动损伤检测和基于振动的参数识别任务，其基本结构为输入层、隐藏层与输出层，多层反向传播网络是模态分析中最常用的网络。Chang等首先通过SSI法得到结构的频率和振型，然后推导了该结构的简化模型，通过改变刚度来构建数据集，最后建立CNN模型，用于研究地震作用后的建筑刚度折减，并以双塔钢框架建筑为例进行了振动台试验，验证了该方法的有效性。[58]Oh等提出了一种基于CNN的高层建筑结构健康监测模型，将时域和频域中的顶层风致位移以及频率域中的风速数据作为输入，以反映高层建筑因风荷载而引起的建筑动力特性变化。[59]Yun等提出了一种自适应SSI长短期记忆方法，用于在实时测量的结构响应时程数据中评估模态参数，估计随建筑物因老化和损坏而导致固有频率的变化，并以55层高层建筑为例，验证了该方法的实用性（图3）。[60]CNN无须进行数据预处理或手工特征提取，可以直接从原始数据中学习并提取特征，但CNN模型的选择依然取决于预期的计算时限和样本数据的可用性。[61]

图3 55层建筑验证试验[60]

计算机视觉的兴起也为模态分析提供了新方法，这一流程通常为相机标定、特征提取、目标追踪和位移计算。[62-63]结构位移作为计算机视觉监测的关键参数，可从中提取结构的模态信息，为模态分析提供支持。修晟等将加速度传感器与相机相结合，构建了一种精确估计结构关键位移响应的方法，并对混凝土框架结构的振动台试验对该方法进行了试验验证，结果表明该融合方法可获取更丰富的模态特征信息并在一个小型钢塔的试验初步证实了该方法的潜力。[64]此外，深度学习可与计算机视觉结合提高位移监测精度。Gao等提出了一种混合结构位移估计方法，将基于深度学习的密集光流与相关模板匹配相结合，提高了位移估计精度和鲁棒性，通过三层钢筋混凝土结构的室内振动台试验与冷弯型钢墙体系统的室外振动台试验验证了该方法的有效性。[65]基于计算机视觉的建筑模态监测研究仍在较为理想环境下的试验研究阶段，如何提高其在真实高层建筑模态监测中的应用效率和可靠度是后续研究的重点。

2 超高层建筑监测系统

2.1 传统监测系统

传统超高层监测系统通常包括传感器和数据传输系统，其中传感器负责收集的原始数据包括载荷（结构温度、风压和地面运动）、结构响应（沉降、倾斜、位移、应变和加速度）和环境因素（温度、湿度、太阳辐射等），数据传输系统由结构上的若干个独立单元组成。依据传感器所采集数据类型的差异，可将传感器分为三类：用于测量结构加速度和位移等动态振动的运动学传感器，用于静态测量结构应力、倾斜度和变形的机械传感器，用于记录风载荷和温度作用的环境传感器。

近二十年来，全球卫星导航系统（GNSS）与光纤传感系统在结构健康监测中得到了广泛的应用。[66-68]GNSS较于传统的加速度计具有更高的性能，可在不受天气影响的同时对结构进行长期、实时的高精度变形监测。[69]GNSS的定位精度受到大气误差、观测噪声、卫星几何形状等因素的影响。为了识别结构的真实振动，有必要消除原始观测中的噪声，对GNSS测量精度进行全面评估。[70]光纤传感系统以光纤光栅（FBG）（图4）为代表。FBG传感器的工作原理是当光沿光纤长度通过时，会产生窄带反射光，反射光波长随应变和温度的变化呈线性变化，使得FBG传感器能够有效地监测结构的局部应变和温度。FBG传感器具有响应快、质量轻、耐腐蚀等优点，但难以调解波长偏移，并且布设和维护成本极高。

图4 青马桥上的光纤光栅应变传感器[71]

此外，一些复杂的超高层监测系统还包括数据处理系统、数据管理系统及结构健康评估系统，[72-73]其中结构性能评估系统分为在线评估和离线评估，在线评估主要是将测量数据和设计值、分析结果以及预定的阈值和模式进行比较，以提供对结构条件的及时评估，离线评估则结合各种基于模型和数据驱动的算法，进行载荷识别、模态识别以及损伤诊断和预测。

现代超高层监测须收集大量数据以保证结果的有效性。传统监测系统中接触式有线传感器的布线复杂且设备成本极大，[74]尽管接触式无线传感器不存在布线问题，但在数据传输方面依然面临挑战。一方面，接触式传感器安装须耗费大量人力物力，且需长期维护，另一方面，这些传感器测量数据离散、空间分辨率低，限制了接触式传感器在大尺度结构监测的有效性。

2.2 新型监测系统

新型监测系统以非接触式传感系统为主，在使用接触式监测技术时，传感器与结构之间的物理接触易造成结构的干扰，传感器的精度和测量范围有限。为了克服这些问题，非接触式传感器技术被引入到高层建筑结构模态的测量中。该技术通过使用激光测振仪、红外线测温计、数字摄像机等非接触式测量方法，实现对结构振动的实时监测和分析。相比于接触式传感器技术，非接触式传感器技术可避免传感器与结构之间的物理接触，减小了对结构的干扰。

非接触式监测技术以其经济性和全局性的监测优势发展成为新型结构监测技术，新型监测系统由机器平台、非接触式传感器、数据传输系统构成，其中机器平台包括无人机[75]、无人车[76]、无人艇[77]等，基于光学的非接触式传感器主要为激光和可见光传感器，由于大多数机器人平台无法实时处理数据，因此需要无线视频发射器将采集到的数据传送到计算机进行导航和数据处理。

激光多普勒测振仪（LDV）（图5）[78]是常见的激光传感器，利用外差干涉原理和多普勒效应来测量物体表面振动。LDV通过分束器发射两条激光，一条射向被测振动目标，振动体的往复运动使激光发生多普勒频移，另一条射向合路器，与从振动体反射的激光汇合于合路器，最后通过检测器确定物体的振幅和频率。LDV仅适用于近距离的单点结构位移测量。

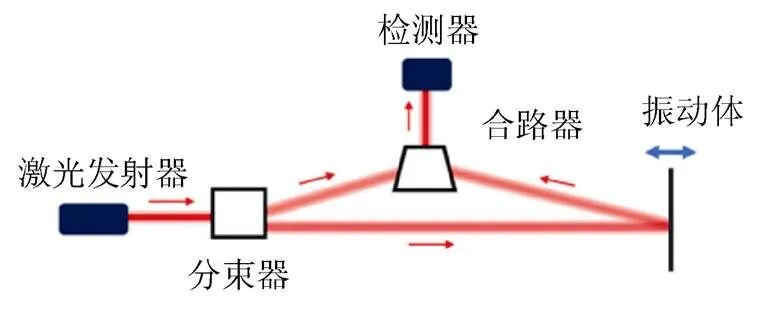
图5 LDV激光传输过程[78]

可见光传感器根据感光元件的不同分为CCD和CMOS传感器，与长焦镜头搭配不仅能限制视野，还能提高特定区域的图像分辨率。可见光传感器通过采集的一系列图像或视频数据来将被测物的点、图案或边界作为特征，结合摄影测量学技术测得运动物体的位移，进而计算被测物的模态信息。该过程主要包括四个步骤:相机校准、图像视频采集、位移场测量和模态计算。

LDV与高分辨率相机价格昂贵，一种廉价的、具有深度传感功能的RGB-D相机提供了以前只能通过上述昂贵传感器才能获得的功能，Kinect是微软于2010年发布的一款RGB-D相机，随后微软公司于2014年推出了Kinect 2.0（图6）[79]。包括一个深度传感器，一个红外发射器和1080 P彩色摄像机及4阵列麦克风。大部分RGB-D相机均基于红外技术，易受太阳直射光的干扰，这限制了其室外的应用，目前RGB-D传感技术仍在不断发展，为室外结构监测提供高质量的数据。[80]

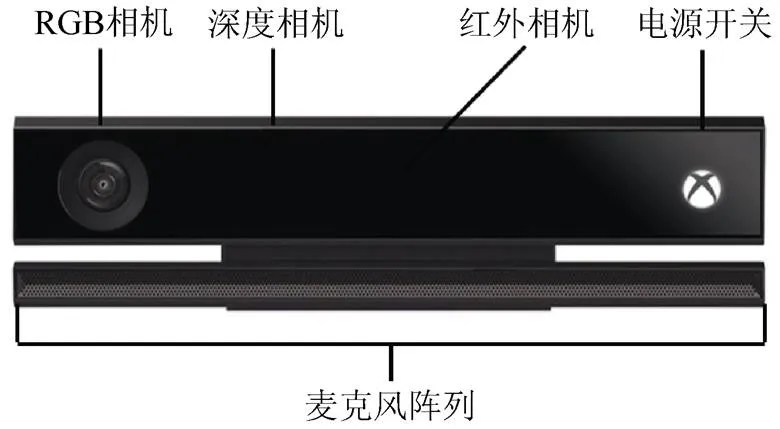
图6 Kinect 2.0传感器

新型监测系统的部署成本更低，时间效率更高，尽管基于视觉的方法具有优势，但目前实际使用新型监测系统对超高层建筑进行监测的案例较少，大部分研究还集中于室内试验[81]或桥梁结构[82]，且其测量性能取决于许多因素，如光照、相机的像素分辨率、相机视点等。不论是传统监测系统还是新型监测系统，环境因素仍是最具挑战的问题。

3 动力特性识别方法的应用

时域、频域和时频域方法已成功应用于工程实践中，以数据驱动为核心的超高层建筑结构模态分析已取得了一些成果，部分总结如表1所示。尽管采用不同类型的识别算法可以进行可靠的识别，但由于超高层结构的复杂性，其振动幅度和特性的变化以及环境因素如温度和湿度等的影响，现有复杂结构的模态本身可能存在不确定性。因此，在进行结构状态监测时，须要采用多种方法以获得更为准确和可靠的结果。为了获得高准确性的结构状态监测信息，可以通过识别不同阶段的监测数据并将其与有限元模型进行比较来解决模态差异性的问题。例如，Li等采用FDD和随机减量法估计了台北101大厦的模态参数，并将两种方法的计算结果与高层结构的有限元模型进行比较，评估了该超高层的抗震性能。[83]文献[84-85]介绍了也通过精准参数建模的有限元模型作为参考来评估模态属性。

除常规的传感器外，主动质量阻尼器[95]、钢管叠层黏弹性阻尼器[96]、涡流调谐质量阻尼器[97]等阻尼器和各类振动控制技术[98-99]也已广泛应用于超高层建筑，可验证常规环境和台风、地震等极端环境振动下的耗能情况和模态控制性能，以此来进一步分析超高层建筑结构的损伤特征。上述实际研究结果表明：超高层建筑结构的阻尼在细微环境振动激励下变化较小，但当在强风和地震强激励下阻尼会表现出幅值依赖性和显著变化，且结构振动会从平稳变得非平稳。

上海国金中心、台北101、广州利通广场、深圳地王大厦、以及深圳平安金融中心等超高层建筑已经建立了较为完备的超高层结构健康监测系统，并取得了大量有价值的阶段性研究成果。然而，在实际工程中的应用效果还不够理想。随着超高层建筑安装各种传感器的数量不断增加，这些建筑的多源异构数据具有大数据的特征。这些数据采集迅速，积累长期，包含大量噪声，还包括文本和图片等非结构化数据。因此目前亟须通过多种来源的异构信息进行综合分析和评估以识别潜在损伤，从而做出安全评估和智能决策，实现实时感知、识别、诊断、评估建筑结构的损伤和安全状态，防范未来可能出现的安全问题。

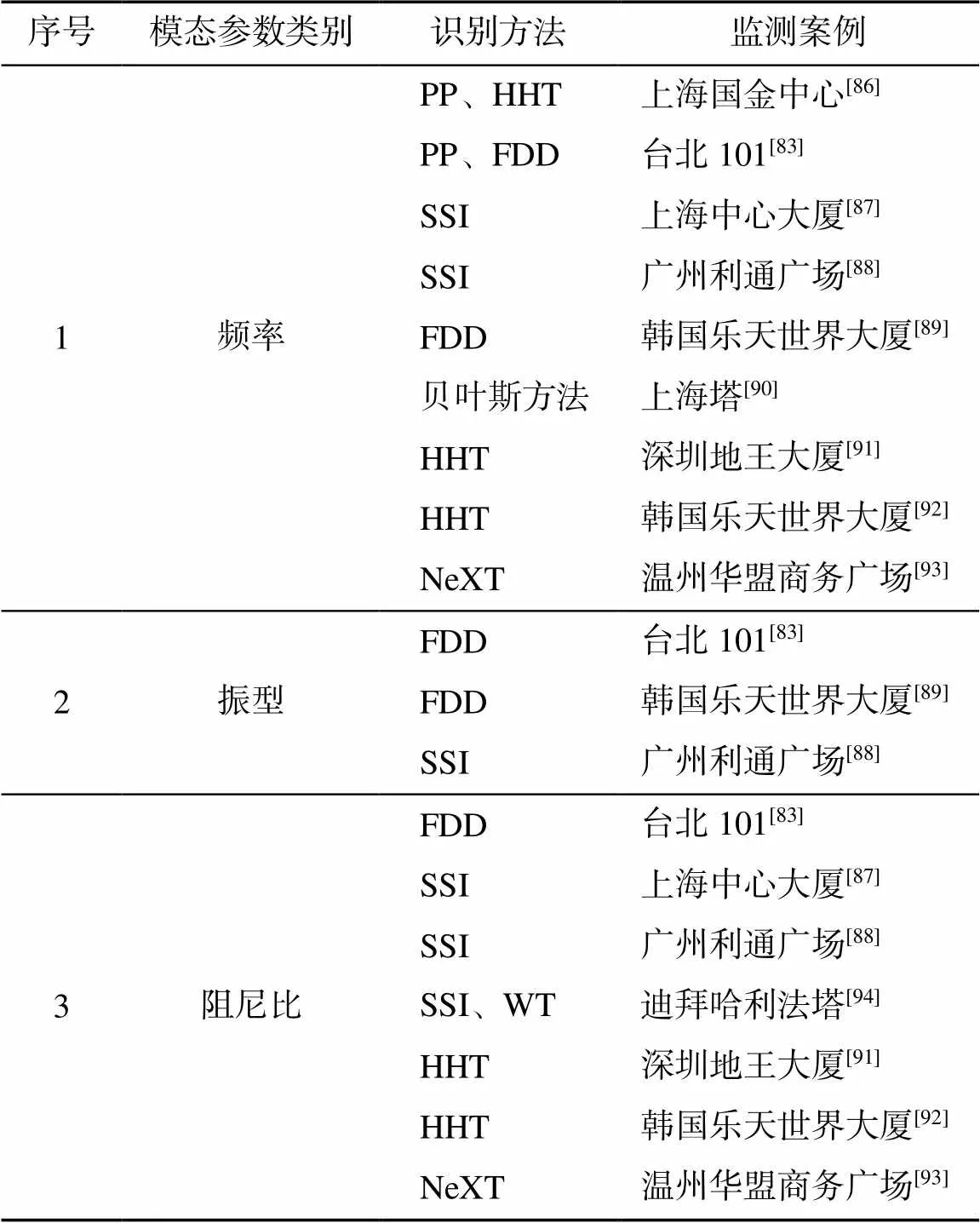
表1 典型超高层动力特性识别方法应用案例

4 结束语

在介绍了超高层建筑动力特性方法的研究背景和意义的基础上，分析了当前超高层建筑动力特性监测的主要方法，介绍了超高层建筑监测系统的设计和实现，包括常用的传感器和新兴技术的应用。目前超高层建筑动力特性长期监测仍面临一定的挑战，如传感器安装位置和数量的选择、数据处理和分析的复杂性等。未来应进一步探索新的识别方法和监测技术，以提高超高层建筑动力特性识别和监测系统的精确度和可靠性。最后基于上述分析，得出以下结论：

1）频域、时域和时频域分析方法均存在各自优缺点，因此，为在实际应用中获得更准确、可靠的结果，须根据具体情况和需求综合考虑，选择合适的分析方法进行结构模态识别。

2）超高层建筑监测须对多个传感器的监测数据进行处理评估，各类异构传感器存在数据冗余或不完整等问题，同类传感器数据中噪声含量也可能不同。因此，须要建立超高层监测数据融合框架以准确、高效地融合多源传感信息。这对做出科学决策具有重要发展意义。

3）随着高性能硬件计算能力的提升和数据采集技术的快速发展，以深度学习为代表的数据处理方法可从原始数据中学习高度抽象的特征，为动力特性识别提供了新的途径。因此，传统的动力特性识别方法面临的问题也可以通过新的数据处理方法得到解决。例如，深度学习可以从传感器所采集的数据中提取出特征，从而减少环境噪声对识别结果的影响，同时也可以提高计算效率和准确度。因此，未来可通过引入新的数据处理技术，改善传统动力特性识别方法的缺陷。

4）非接触式传感器可获取全局或局部数据，且无需与超高层建筑物理接触，相较于接触式传感器效率和鲁棒性更高。因此，非接触式传感技术是未来超高层监测技术的主要方向。此外，无人机、无人车作为非接触式传感器的搭载平台，扩大了监测应用场景范围，属于非接触式传感技术的重点研究方向。

5）无论是接触式传感器还是非接触式传感器，都存在其各自的局限性。因此，传感器的结合应用是超高层建筑监测的趋势。当前大多数传感器的结合方式是将加速度计与其他传感器相结合，未来须聚焦于各类接触式、非接触式传感器的结合应用，使监测数据更全面、准确。

[1] Council on Tall Buildings and Urban Habitat. Database of countries by number of 150m+ building[EB/OL]. (2023-03-27) [2023-11-22]. https://www.skyscrapercenter.com/countrie.

[2] GARCíA-MACíAS E, UBERTINI F. Automated operational modal analysis and ambient noise deconvolution interferometry for the full structural identification of historic towers: A case study of the Sciri Tower in Perugia, Italy[J/OL]. Engineering Structures, 2020, 215[2023-11-22]. https://doi.org/10.1016/j.engstruct.2020. 110615.

[3] 伊廷华, 周广东, 曲春绪, 等. 结构运营模态测–辨相和理论[J]. 土木工程学报, 2020, 53(10): 72–81.

[4] 王凌波, 王秋玲, 朱钊, 等. 桥梁健康监测技术研究现状及展望[J]. 中国公路学报, 2021, 34(12): 25–45.

[5] SPENCER B F, HOSKERE V, NARAZAKI Y. Advances in computer vision-based civil infrastructure inspection and monitoring[J]. Engineering, 2019, 5(2): 199–222.

[6] 徐阳, 金晓威, 李惠. 土木工程智能科学与技术研究现状及展望[J]. 建筑结构学报, 2022, 43(9): 23–35.

[7] ZHONG S C, ZHONG J F, ZHANG Q K, et al. Quasi-optical coherence vibration tomography technique for damage detection in beam-like structures based on auxiliary mass induced frequency shift[J]. Mechanical Systems and Signal Processing, 2017, 93: 241–254.

[8] QIAO L. Structural damage detection using signal-based pattern recognition[D]. Manhattan: Kansas State University, 2009.

[9] NANDAGOPALAN S. Engineering applications of correlation and spectral analysis[J]. Technometrics, 1994, 36(2): 220–221.

[10] SHIH C Y, TSUEI Y G, ALLEMANG R J, et al. Complex mode indication function and its applications to spatial domain parameter estimation[J]. Mechanical Systems and Signal Processing, 1988, 2(4): 367–377.

[11] GUILLAUME P, VERBOVEN P, VANLANDUIT S. Frequency- domain maximum likelihood identification of modal parameters with confidence intervals[J]. Noise and Vibration Engineering, 1998, 1: 359–366.

[12] BRINCKER R, ZHANG L, ANDERSEN P. Modal identification from ambient responses using frequency domain decomposition[C]// Proceedings of the 18th International Modal Analysis Conference, 2000: 625–630.

[13] PIOLDI F, FERRARI R, RIZZI E. Output-only modal dynamic identification of frames by a refined FDD algorithm at seismic input and high damping[J]. Mechanical Systems and Signal Processing, 2016, 68: 265–291.

[14] PIOLDI F, FERRARI R, RIZZI E. Seismic FDD modal identification and monitoring of building properties from real strong-motion structural response signals[J/OL]. Structural Control and Health Monitoring, 2017, 24[2023-11-27]. https://doi.org/10. 1002/stc.1982.

[15] YUN D Y, KIM D, KIM M, et al. Field measurements for identification of modal parameters for high-rise buildings under construction or in use[J/OL]. Automation in Construction, 2021, 121[2023-11-23]. https://doi.org/10.1016/j.autcon.2010.103446.

[16] HASAN M D B A, AHMAD Z A B, LEONG M S, et al. Enhanced frequency domain decomposition algorithm: a review of a recent development for unbiased damping ratio estimates[J]. Journal of Vibroengineering, 2018, 20: 51919–51936.

[17] 周思达, 曹博远, 周小陈. 结构应变模态参数辨识的最小二乘复频域方法[J]. 噪声与振动控制, 2017, 37(6): 17–22.

[18] PEETERS B, VAN DER AUWERAER H, GUILLAUME P, et al. The PolyMAX frequency-domain method: a new standard for modal parameter estimation[J]. Shock and Vibration, 2004, 11(3): 395–409.

[19] EL-KAFAFY M, GUILLAUME P, PEETERS B, et al. Advanced frequency-domain modal analysis for dealing with measurement noise and parameter uncertainty[C]//Proceedings of the 30th International Modal Analysis Conference. 2012: 179–199.

[20] 章国稳, 汤宝平, 陈卓. 多参考最小二乘复频域法的数值问题分析及优化[J]. 振动工程学报, 2021, 34(4): 690–696.

[21] LIU C W, WU J Z, ZHANG Y G. Review and prospect on modal parameter identification of spatial lattice structure based on ambient excitation[J]. Applied Mechanics and Materials, 2011, 94/95/96: 1271–1277.

[22] MAGALHãES F, CAETANO E, CUNHA Á. Challenges in the application of stochastic modal identification methods to a cable-stayed bridge[J]. Journal of Bridge Engineering, 2007, 12: 6746–6754.

[23] JAMES ⅢG H, CARNE T G, LAUFFER J P. The natural excitation technique (NExT) for modal parameter extraction from operating wind turbines[R]. Technical Report: sand-92-1666 on DE 93010611. Albuquerque: Sandia National Labs, 1993.

[24] ANDERSEN P. Identification of civil engineering structures using vector ARMA models[D]. Aalborg: Aalborg University, 1997.

[25] DE MOOR B L R, VAN OVERSCHEE P, SUYKENS O J. Subspace algorithms for system identification and stochastic realization[C]//Proceedings of the International Symposium on Recent Advances in Mathematical Theory of Systems, Control, Networks and Signal Processing. 1991: 589–595.

[26] JUANG J N, PAPPA R S. An eigensystem realization algorithm for modal parameter identification and model reduction[J]. Journal of Guidance, Control, and Dynamics, 1985, 8(5): 620–627.

[27] KORDKHEILI S A H, MASSOULEH S H M, HAJIREZAYI S, et al. Experimental identification of closely spaced modes using NExT-ERA[J]. Journal of Sound and Vibration, 2018, 412: 116–129.

[28] CHANG M, PAKZAD S N. Modified natural excitation technique for stochastic modal identification[J]. Journal of Structural Engineering, 2013, 139(10): 1753–1762.

[29] QU C X, YI T H, LI H N. Mode identification by eigensystem realization algorithm through virtual frequency response function[J/OL]. Structural Control and Health Monitoring, 2019, 26(10)[2023-11-23]. https//doi.org/10.1002/stc.2429.

[30] CUNHA A, CAETANO E. Experimental modal analysis of civil engineering structures[J]. Sound and Vibration, 2006, 6(40): 12–20.

[31] VOLD H, KUNDRAT J, ROCKLIN G T, et al. A multi-input modal estimation algorithm for mini-computers[J]. SAE Transactions, 1982, 91: 815–821.

[32] KORDKHEILI S A H, MASSOULEH S H M, HAJIREZAYI S, et al. Experimental identification of closely spaced modes using NExT-ERA[J]. Journal of Sound and Vibration, 2018, 412: 116–129.

[33] BODEUX J B, GOLINVAL J C. Application of ARMAV models to the identification and damage detection of mechanical and civil engineering structures[J]. Smart Materials and Structures, 2001, 10: 3479–489.

[34] BERTHA M, GOLINVAL J C. Identification of non-stationary dynamical systems using multivariate ARMA models[J]. Mechanical Systems and Signal Processing, 2017, 88: 166–179.

[35] SPIRIDONAKOS M D, POULIMENOS A G, FASSOIS S D. Output-only identification and dynamic analysis of time-varying mechanical structures under random excitation: A comparative assessment of parametric methods[J]. Journal of Sound and Vibration, 2010, 329: 7768–7785.

[36] BRINCKER R, ANDERSEN P, JACOBSEN N J. Automated frequency domain decomposition for operational modal analysis[C]// Proceedings of IMAC-XXIV: A Conference & Exposition on Structural Dynamics Society for Experimental Mechanics, 2007: 1–7.

[37] CERAVOLO R, ABBIATI G. Time domain identification of structures: Comparative analysis of output-only methods[J]. Journal of Engineering Mechanics, 2013, 139: 4537–4544.

[38] ZHOU K, LI Q S. Modal identification of high-rise buildings under earthquake excitations via an improved subspace methodology[J/OL]. Journal of Building Engineering, 2022, 52[2023-11-23]. https://doi.org/10.1016/j.jobe.2022.104373.

[39] ZHOU K, LI Q S, HAN X L. Modal identification of civil structures via stochastic subspace algorithm with Monte Carlo-based stabilization diagram[J/OL]. Journal of Structural Engineering, 2022, 148(6)[2023-11-23]. https://doi.org./10.1061/ (ASCE)ST.1943-541X.0003353.

[40] JIN N, YANG Y, DIMITRAKOPOULOS E G, et al. Application of short-time stochastic subspace identification to estimate bridge frequencies from a traversing vehicle[J/OL]. Engineering Structures, 2021, 230[2023-11-23]. https://doi.org/10.1016/j. engstruct.2020.111688.

[41] 李雪艳, 官宇航, 罗铭涛, 等.基于Welch法的协方差随机子空间方法的模态参数识别[J]. 力学学报, 2022, 54(10): 2850–2860.

[42] LI H, YI T, GU M, et al. Evaluation of earthquake-induced structural damages by wavelet transform[J]. Progress in Natural Science, 2009, 19: 4461–470.

[43] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903–995.

[44] SHAN J, ZHANG H, SHI W, et al. Health monitoring and field-testing of high-rise buildings: A review[J]. Structural Concrete, 2020, 21: 41272–41285.

[45] PENG Z, PETER W T, CHU F. A comparison study of improved Hilbert-Huang transform and wavelet transform: Application to fault diagnosis for rolling bearing[J]. Mechanical Systems and Signal Processing, 2005, 19: 5974–5988.

[46] 柳絮, 王坚, 李文. 集成变分模态分解和希尔伯特-黄变换的结构振动时频提取模型[J]. 武汉大学学报(信息科学版), 2021, 46(11): 1686–1692.

[47] 孙苗, 杨钧凯, 吴立. 改进希尔伯特-黄变换含噪振动信号时频分析[J/OL]. 上海交通大学学报(2023-03-21)[2023-11-24]. https://doi.org/10.16183/j.cnki.jsjtu.2022.255.

[48] RAFIEI M H, ADELI H. A novel machine learning-based algorithm to detect damage in high-rise building structures[J/OL]. Structural Design of Tall and Special Buildings, 2017, 26(18) [2023-11-23]. https://doi.org/10.1002/tal.1400.

[49] ZHOU K, XIE D L, XU K, et al. A machine learning-based stochastic subspace approach for operational modal analysis of civil structures[J/OL]. Journal of Building Engineering, 2023, 76[2023-11-23]. https://doi.org/10.1016/j.jobe.2023.107187.

[50] GEORGIOUDAKIS M, PLEVRIS V. Response spectrum analysis of multi-story shear buildings using machine learning techniques[J]. Computation, 2023, 11(7)[2023-11-23]. https://doi. org/10.3390/computation.11070126.

[51] KATAFYGIOTIS L S, YUEN K V. Bayesian spectral density approach for modal updating using ambient data[J]. Earthquake Engineering & Structural Dynamics, 2001, 30(8): 1103–1123.

[52] NI Y, LU X, LU W. Operational modal analysis of a high-rise multi-function building with dampers by a Bayesian approach[J]. Mechanical Systems and Signal Processing, 2017, 86: 286–307.

[53] ZHANG F L, NI Y Q, NI Y C, et al. Operational modal analysis of Canton Tower by a fast frequency domain Bayesian method[J]. Smart Structures and Systems, 2016, 17: 2209–2230.

[54] LI B, AU S K. An expectation-maximization algorithm for Bayesian operational modal analysis with multiple (possibly close) modes[J]. Mechanical Systems and Signal Processing, 2019, 132: 490–511.

[55] AU S K, ZHANG F L, NI Y C. Bayesian operational modal analysis: theory, computation, practice[J]. Computers & Structures, 2013, 126: 3–14.

[56] Perez-Ramirez C A, Amezquita-Sanchez J P, Valtierra-Rodriguez M, et al. Recurrent neural network model with Bayesian training and mutual information for response prediction of large buildings[J]. Engineering Structures, 2019, 178: 603–615.

[57] 熊红凯, 高星, 李劭辉, 等. 可解释化、结构化、多模态化的深度神经网络[J]. 模式识别与人工智能, 2018, 31(1): 1–11.

[58] CHANG C M, LIN T K, CHANG C W. Applications of neural network models for structural health monitoring based on derived modal properties[J]. Measurement, 2018, 129: 457–470.

[59] OH B K, GLISIC B, KIM Y, et al. Convolutional neural network-based wind-induced response estimation model for tall buildings[J]. Computer-Aided Civil and Infrastructure Engineering,2019, 34: 10843–10858.

[60] YUN D Y, SHIM H B, PARK H S. SSI-LSTM network for adaptive operational modal analysis of building structures[J/OL]. Mechanical Systems and Signal Processing, 2023, 195[2023-11-23]. https://doi.org/j.ymssp.2023.1103.06.

[61] HOSSAIN M S, ONG Z C, ISMAIL Z, et al. Artificial neural networks for vibration based inverse parametric identifications: A review[J]. Applied Soft Computing, 2017, 52: 203–219.

[62] 叶肖伟, 董传智. 基于计算机视觉的结构位移监测综述[J].中国公路学报, 2019, 32(11): 21–39.

[63] 杨娜, 汪德佳, 李天昊,等. 基于计算机视觉方法的古建筑变形监测[J]. 建筑结构学报, 2023, 44(1): 192–202.

[64] 修晟, 张愿, 单伽锃. 基于视觉和振动监测数据融合的结构动态位移识别及其试验验证[J]. 工程力学, 2023, 40(11): 90–98.

[65] GAO X, JI X, ZHANG Y, et al. Structural displacement estimation by a hybrid computer vision approach[J/OL]. Mechanical Systems and Signal Processing, 2023, 204[2023-11-24]. https:// doi.org/10.1016/j.ymssp.2023.110754.

[66] 胡卫华, 唐德徽, 李俊燕, 等. 基于分布式同步采集的赛格大厦结构动力学参数识别[J]. 建筑结构学报, 2022, 43(10): 76–84.

[67] 吴睿, 廖聿宸, 宗周红, 等. 基于GNSS信号的随机子空间模态参数识别方法[J]. 东南大学学报(自然科学版), 2020, 50(6): 1045–1051.

[68] 朱珊, 周文杰, 李晓莹. 混凝土健康监测技术综述[J]. 建筑结构, 2022, 52(增刊1): 2248–2252.

[69] SHEN N, CHEN L, LIU J, et al. A review of global navigation satellite system (GNSS)-based dynamic monitoring technologies for structural health monitoring[J/OL]. Remote Sensing, 2019, 11(9)[2023-11-24]. https://doi.org/10.3390/rs1109001. 1.

[70] YU J, MENG X, YAN B, et al. Global Navigation Satellite System-based positioning technology for structural health monitoring: a review[J/OL]. Structural Control and Health Monitoring, 2020, 27(1)[2023-11-24]. https://doi.org/10.1002/ stc.2467.

[71] MOYO P, BROWNJOHN J M W, SURESH R, et al. Development of fiber Bragg grating sensors for monitoring civil infrastructure[J]. Engineering Structures, 2005, 27(12): 1828–1834.

[72] 张兴斌, 杨昕光, 潘蓉, 等. 土木工程智能化监测评估系统的理论研究及应用[J]. 工业建筑, 2021, 51(12): 102–106.

[73] 焦柯, 赖鸿立, 彭子祥, 等. 基于物联网的既有建筑全生命周期安全运维服务系统关键技术研究[J]. 工业建筑, 2021, 51(10): 201–210.

[74] 伊廷华, 李宏男, 顾明. 结构健康监测中基于多重优化策略的传感器布置方法[J]. 建筑结构学报, 2011, 32(12): 217–223.

[75] 刘春, 艾克然木·艾克拜尔, 蔡天池. 面向建筑健康监测的无人机自主巡检与裂缝识别[J]. 同济大学学报(自然科学版), 2022, 50(7): 921–932.

[76] 周梦飞, 王子洋, 杨家富. 应用于无人车的三维点云分类方法研究综述[J]. 传感技术学报, 2022, 35(7): 931–937.

[77] 普东东, 欧阳永忠, 马晓宇. 无人船监测与测量技术进展[J].海洋测绘, 2021, 41(1): 8–12.

[78] LI Y, DIEUSSAERT E, BAETS R. Miniaturization of laser Doppler vibrometers: a review[J/OL]. Sensors, 2022, 22(13) [2023-11-24]. https://doi.org/10.3390/s22134735.

[79] 涂淑琴, 薛月菊, 梁云等. RGB-D图像分类方法研究综述[J]. 激光与光电子学进展, 2016, 53(6): 35–48.

[80] ABDELBARR M, CHEN Y L, JAHANSHAHI M R, et al. 3D dynamic displacement-field measurement for structural health monitoring using inexpensive RGB-D based sensor[J/OL]. Smart Materials and Structures, 2017, 26(12)[2023-11-24]. https://doi. org/10.1088/1361-665x/aa9450.

[81] DONG C Z, CELIK O, CATBAS F N. Marker-free monitoring of the grandstand structures and modal identification using computer vision methods[J]. Structural Health Monitoring, 2019, 18(5): 1491–1509.

[82] FENG D, FENG M Q. Experimental validation of cost-effective vision-based structural health monitoring[J]. Mechanical Systems and Signal Processing, 2017, 88: 199–211.

[83] LI Q, ZHI L H, TUAN A Y, et al. Dynamic behavior of Taipei 101 tower: Field measurement and numerical analysis[J]. Journal of Structural Engineering, 2011, 137: 1143–1155.

[84] ZHI L, LI Q, WU J, et al. Field monitoring of wind effects on a super-tall building during typhoons[J]. Wind & Structures, 2011, 14(3): 253–283.

[85] HE Y, HAN X, LI Q, et al. Monitoring of wind effects on 600 m high Ping-An Finance Center during Typhoon Haima[J]. Engineering Structures, 2018, 167: 308–326.

[86] SHI W, SHAN J, LU X. Modal identification of Shanghai World Financial Center both from free and ambient vibration response[J]. Engineering Structures, 2012, 36: 14–26.

[87] XIE B, LUO X Q, ZHANG Q L, et al. Dynamic response evaluation of the Shanghai Tower in along-and across-wind directions during super typhoon Lekima[J/OL]. Journal of Building Engineering, 2023, 65[2023-11-24]. https://doi.org/10. 1016/j.jobe.2022.1058808.

[88] HE Y, LI Z, FU J, et al. Enhancing the performance of stochastic subspace identification method via energy-oriented categorization of modal components[J/OL]. Engineering Structures, 2021, 233 [2023-11-24]. https://doi.org/j.engstruct.2021.111917.

[89] PARK H S, OH B K. Real-time structural health monitoring of a supertall building under construction based on visual modal identification strategy[J]. Automation in Construction, 2018, 85: 273–289.

[90] ZHANG F, XIONG H, SHI W, et al. Structural health monitoring of Shanghai Tower during different stages using a Bayesian approach[J]. Structural Control and Health Monitoring, 2016, 23(11): 1366–1384.

[91] XU Y L, CHEN S, ZHANG R. Modal identification of Di Wang Building under typhoon York using the Hilbert-Huang transform method[J]. The Structural Design of Tall and Special Buildings, 2003, 12: 121–147.

[92] AMEZQUITA-SANCHEZ J P, PARK H S, ADELI H. A novel methodology for modal parameters identification of large smart structures using MUSIC, empirical wavelet transform, and Hilbert transform[J]. Engineering Structures, 2017, 147: 148–159.

[93] WANG C, LI Z, HU L, et al. Field research on the wind- induced response of a super high-rise building under typhoon[J/OL]. Applied Sciences, 2019, 9(11)[2023-11-24]. https://doi.org/10.3390/ app9112180.

[94] GUO Y, KWON D K, KAREEM A. Near-real-time hybrid system identification framework for civil structures with application to Burj Khalifa[J/OL]. Journal of Structural Engineering,2016, 142(2)[2023-11-24]. https://doi.org/10.1061/(ASCE)ST.1943- 541x.0001402.

[95] 刘彦辉, 谭平, 周福霖, 等. 广州电视塔直线电机驱动的主动质量阻尼器动力特性研究[J]. 建筑结构学报, 2015, 36(4): 126–132.

[96] 周云, 吴胜, 李家乐. 钢管叠层黏弹性阻尼器设计方法[J]. 建筑结构学报, 2023, 44(3): 79–86.

[97] LU X, ZHANG Q, WU W, et al. Data-driven two-level performance evaluation of eddy-current tuned mass damper for building structures using shaking table and field testing[J]. Computer-Aided Civil and Infrastructure Engineering, 2019, 34: 138–157.

[98] 滕军, 幸厚冰. 京基100大厦AMD控制系统在线计算关键技术研究[J]. 振动与冲击, 2011, 30(11): 230–235.

[99] 滕军, 陈朝骏, 幸厚冰, 等. 考虑结构高阶振型信息的AMD低维控制器设计[J]. 振动工程学报, 2016, 29(6): 1048–1056.

Research Progress on Dynamic Characteristic Monitoring Methods of Super High-Rise Buildings

WU Yongjingbang1,2,3JIN Nan1,2,3SHI Zhongqi1,2,3YUE Qingrui1,2,3ZHONG Rumian1,2,3

(1. Shenzhen Urban Public Safety and Technology Institute, Shenzhen 518046, China; 2. Key Laboratory for Urban Safety Risk Monitoring and Early Warning of Emergency Management Department, Shenzhen 518038, China; 3. Safe Urban Development Institute of Science and Technology (Shenzhen), Shenzhen 518046, China)

The acceleration of urbanization has led to a sharp rise in the number of super high-rise buildings in China. However, the issues related to the operation and maintenance of those buildings have become increasingly prominent. As a result, extensive attention to the service safety of super high-rise buildings have been paid. Summarizing and analyzing the theoretical methods and practical applications of identifying dynamic characteristic parameters of super high-rise buildings, the characteristics of super high-rise building structure monitoring technique, which were represented by the time domain, frequency domain, time-frequency domain and the new modal recognition method. Subsequently, the advantages and limitations of each monitoring method and system were compared. Simultaneously, the main issues in the current monitoring technique for super high-rise buildings were summed and development trends of monitoring methods were discussed. Eventually, the application of dynamic characteristic identification in the monitoring of super high-rise buildings was sorted out which would be expected to present a reference basis for improcing accurcy, effectiveness and reliability of dynamic characteristic identification for super high-rise buildings and provide reference to improving operation and maintenance levels for super high-rise buildings in China.

super high-rise building; dynamic characteristic; parameter identification; health monitoring; service safety

伍永靖邦, 金楠, 施钟淇, 等. 超高层建筑动力特性监测方法研究进展[J]. 工业建筑, 2024, 54(1): 1-10. WU YJB, JIN N, SHI Z Q, et al. Research Progress on Dynamic Characteristic Monitoring Methods of Super High-Rise Buildings[J]. Industrial Construction, 2024, 54(1): 1-10 (in Chinese).

10.3724/j.gyjzG23071809

*国家重点研发计划项目（2022YFC3801203）；中国博士后基金资助（2022M720416）。

伍永靖邦，硕士，研究方向为结构健康监测。

金楠，博士，研究方向为结构健康监测，jinnan@szsti.org。

2023-07-18