基于SHA-256和Arnold映射的量子Logistic映射图像加密算法

杨宇光,王嘉伟

(北京工业大学 信息学部,北京 101124)

互联网能提供文字、图像、声音、动画等数据信息,互联网上的数据很容易被窃取、篡改、复制和非法传播.图像在多媒体通信中有重要作用,且许多图片涉及个人隐私或国家机密,因此图像保护尤为重要.图像具有数据量大、冗余多、相关性强的特点,传统的加密算法不适合图像加密.图像加密是保持数据安全的有效手段,图像加密能在几乎无任何细节损失情况下将其还原.研究人员提出了许多基于新技术的图像加密方法,如压缩感知[1-5]、混沌系统[6-10]、元胞自动机[11-14]、脱氧核糖核酸编码[15-17]等.为了提高图像的抗攻击能力,该文拟提出基于SHA-256和Arnold映射的量子Logistic映射图像加密算法.

1 相关知识

1.1 SHA-256

SHA-256是一种密码散列函数,即一种哈希函数.SHA-256对初始值非常敏感,使不同图像对应不同的哈希值,能增强图像加密的随机性.

1.2 Arnold映射

Arnold映射是混沌置乱中使用较多的一种方法.Arnold映射通过改变元素位置实现图像的置乱处理.

Arnold映射的原始公式为

其中:xn,yn为变换前像素的位置坐标;xn+1,yn+1为变换后像素的位置坐标.

将原始公式数字化后,得到如下映射

其中:a,b为参数;L为图像的宽度.

1.3 量子Logistic映射

Logistic映射[18]的定义式为

其中:μ∈(0,4),xn∈(0,1).当3.569 945 6＜μ≤4时,Logistic映射处于混沌状态.

将量子态引入混沌系统,形成量子Logistic映射[19],其定义式为

其中:β,r为控制参数.

2 基于SHA-256和Arnold映射的量子Logistic映射图像加密算法

2.1 图像加密算法

基于SHA-256和Arnold映射,该文提出量子Logistic映射图像加密算法,其结构如图1所示.

2.2 图像加密过程

图像加密过程的具体步骤如下.

步骤1对给定M×N的图像A,在其列坐标N/2处进行竖直切割,得到两个图像B和C,两个图像的大小均为M×N/2.令m=M,n=N/2.

步骤2用SHA-256求图像B的哈希值.对第1,4,7,11,…,256位的哈希值求和得到参数c1,对第2,5,8,…,254位的哈希值求和得到参数c2,对剩下的哈希值求和得到参数c3.将c1,c2,c3作为xn,yn,zn的初始值代入式(4)得到xn+1,yn+1,zn+1,然后将xn+1,yn+1,zn+1作为Arnold映射中的a,b,N的初始值且对图像C进行置乱处理.

步骤3图像C置乱后,用SHA-256求其哈希值.首先对得到的256位哈希值的奇数位求和得到参数d1,其次对剩余的哈希值的奇数位求和得到参数d2,最后将剩下的哈希值相加得到参数d3.

步骤4将参数c1,c2,c3及参数d1,d2,d3代入下式

得到x0,y0,z0.

步骤5将x0,y0,z0作为初始值代入式(4),丢弃前500个值后得到混沌序列x,y,z.

步骤6将混沌序列x,y,z代入下式

得到混沌序列X,Y,Z.

步骤7使用馄饨系列X,Y分别对图像B进行行、列混淆,得到图像D.使用混沌系列Y,Z分别对图像C进行行、列混淆得到图像E.

步骤8将图像D和图像E合并,得到加密图像F.

2.3 图像解密过程

图像解密过程的具体步骤如下.

步骤1在密文图像F的列坐标N/2处进行竖直切割,获得图像D'和E'.

步骤2用公钥对图像E'进行逆置乱操作,得到量子Logistic映射的初始值.

步骤3将初始值代入量子Logistic映射,丢弃前500个值后得到混沌序列x,y,z.

步骤4将混沌序列x,y,z代入式(6)得到混沌序列X,Y,Z.

步骤5通过混沌序列X对图像D'进行行混淆的逆操作,得到图像B'.

步骤6通过混沌序列Y对图像E'进行列混淆的逆操作,得到图像C'.

步骤7对图像B'和图像C'进行合并,得到原始图像A.

3 实验结果及分析

实验硬件为:12th Gen Intel(R)Core(TM)i5-12400F 2.50 GHz,16 GB RAM.实验软件为:Windows 10,MATLAB R2018a.选用的图像为经典灰度图像.

3.1 加解密实验

使用该文提出的算法对测试图集进行了一系列加解密实验,其中Lena,Cameraman和Pirate的明文图像、密文图像及解密图像如图2所示.由图2可知,密文图像与明文图像毫无关联,解密图像与明文图像基本一致,表明该文算法是无损的.

3.2 直方图分析

直方图描述图像中每个像素出现的次数.一个加密性能好的算法,其直方图是均匀分布的.由图3可看出,加密后图像的直方图是均匀分布的,表明该文算法具有较强的抵抗统计攻击的能力.

3.3 相关性分析

为了评价该文算法的置乱效果,将从水平、垂直和对角线3个方向对明文图像和密文图像进行相关性分析.相关系数的定义式为

其中:xi和为相邻像素的灰度值.

从图4,5可看出,Lena明文图像水平方向、垂直方向及对角线方向的灰度值均集中分布,然而其加密后的密文图像的灰度值则是均匀分布.

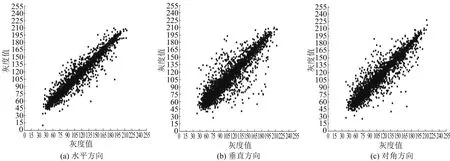
图4 Lena明文图像的平面相关性

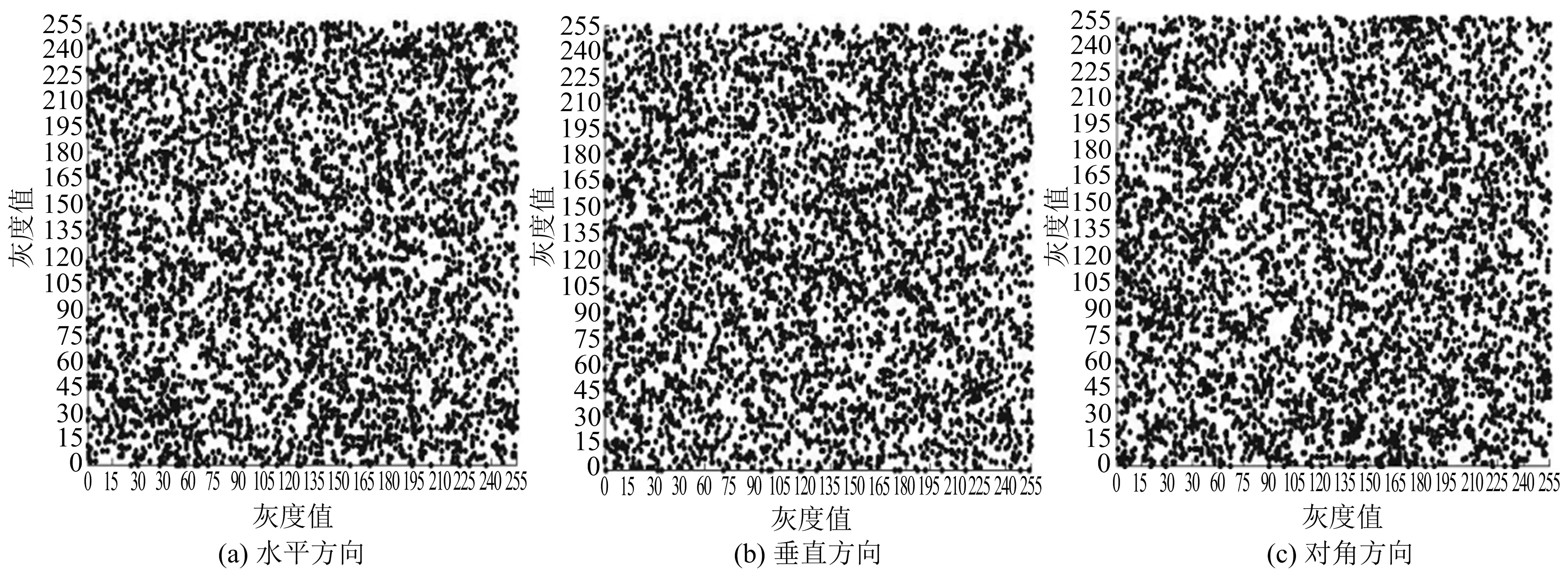
图5 Lena密文图像的平面相关性

表1给出了10类图像不同方向的相关系数.由表1可知:明文图像在3个方向上相关系数均接近1,表明相邻像素间的相关性很强;密文图像的相关系数平均值的绝对值趋近于0,表明相邻像素间几乎无相关性.

表1 10类图像不同方向的相关系数

表2给出了该文算法与其他文献算法的密文图像相关系数对比.由表2可知,该文算法抵抗统计攻击的能力比其他文献算法更强.

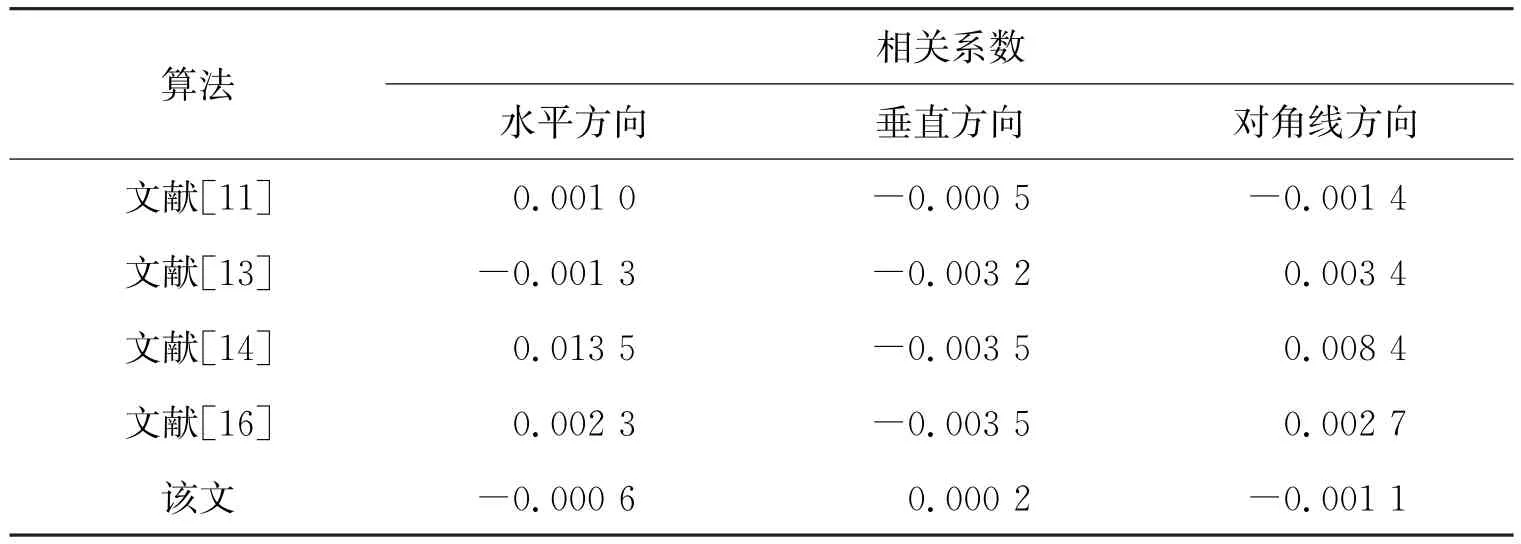
表2 5种算法密文图像相关系数

3.4 安全性能分析

3.4.1 密钥空间

图像加密算法为了能抵抗穷举攻击,其密钥空间必须大于2100.该文算法密钥由两部分组成,一部分为256 bit的哈希值,另一部分为混沌映射的3个初始值,而计算机精度为10-15,所以该文密钥空间为2362,远大于2100.表3给出了5种算法的密钥空间大小.由表3可知,相对于其他文献的密钥空间,该文算法的密钥空间大小适中,能较好地抵抗暴力破解攻击.

表3 5种算法的密钥空间大小

3.4.2 密钥敏感性

若密钥的微小变化能导致密文图像发生较大变化,则认为密钥具有高敏感性.对初始值进行增加和减少10-15以及对迭代次数进行改变,均会导致加密后的图像不能恢复成明文图像.从图6可看出,初始值的微小变化及迭代次数改变后均不能正确解密,表明该文算法具有较强的密钥敏感性.

图6 错误密钥的Lena解密图像

3.5 信息熵

信息熵描述随机性,图像的随机性越强,信息熵越大.信息熵的计算公式为

其中:p(mi)为灰度值mi出现的概率.密文图像的信息熵越接近8,可视信息越少,算法的加密性能越强.

表4给出了5类图像的明文图像及密文图像信息熵.由表4可知,该文算法密文图像的信息熵平均值为7.997,非常接近8,表明该文算法加密性能较强.

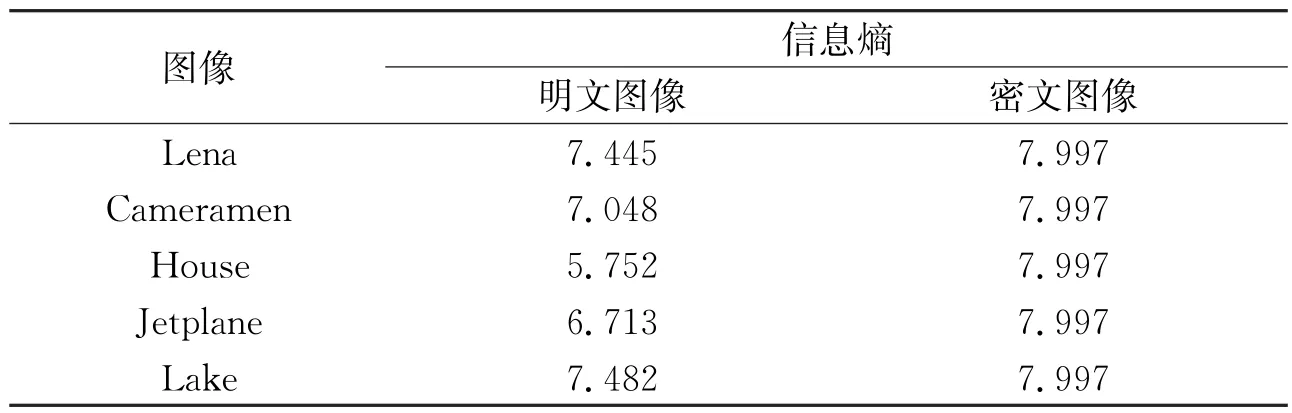
表4 5类图像的明文图像及密文图像的信息熵

3.6 抗差分攻击

从图像加密的角度看,一个优秀的算法,若明文图像出现较小的像素变化,密文图像应该有很大的像素变化.像素变化率(the number of pixels change rate,简称NPCR)和统一平均变化强度(the unified average changing intensity,简称UACI)是评估算法抗差分攻击的两个参量.NPCR和UACI的计算公式分别为

其中:A1(i,j)和A1(i,j)分别表示图像A1和A2在(i,j)处的灰度值;当A1(i,j)=A2(i,j)时,D(i,j)=0,当A1(i,j)≠A2(i,j)时,D(i,j)=1.

表5给出了7类图像的NPCR和UACI.NPCR和UACI的期望值分别为99.61%和33.46%.从表5可看出,该文算法这两个值均接近期望值.

表5 7类图像的NPCR和UACI %

4 结束语

该文提出了基于SHA-256和Arnold映射的量子Logistic映射图像加密算法.实验结果表明:该文算法的解密图像与明文图像基本一致;该文算法具有较强的密钥敏感性;相对于其他文献算法,该文算法具有更强的抵抗统计攻击的能力.