基于流固耦合的水下发球管汇力学及振动特性分析
2024-02-29鞠朋朋柳英明张欢李林
鞠朋朋, 柳英明, 张欢, 李林
(1. 海洋石油工程股份有限公司设计院, 天津 300461; 2中国石油大学(北京)机械与储运工程学院, 北京102249)
近年来,全球油气勘探活动不断向浅水、深水、超深水突破,深水-超深水已成为全球油气勘探的重点领域[1]。水下油气生产系统作为海洋油气开发的主流模式,是指一系列安装在海底并进行石油和天然气开采作业的设备总集,具有投资成本低、开发周期短、投产效益高的特点,是深水油气开发的关键技术[2-3]。深水油气田井口采出流体含水、固体颗粒、CO2以及H2S等杂质,对于钢制的海底混输管道具有腐蚀作用,严重威胁了海底管道的输送安全[4-5]。现阶段主要采用内涂层、添加缓蚀剂的防护措施,防止或减缓管内腐蚀[6],管内固体沉积会通过吸附,阻碍缓蚀剂到达海管表面,降低缓蚀剂作用,因此,通过清管球将沉积物清出海底集输管道,是保障缓蚀剂效率的重要技术手段。深水水下不停产在役清管技术具有作业成本低、可利用生产流体发球、无需长时间停井的优势[7-8]。随着深水油气资源开发力度的加大,水下清管将成为必然趋势[9]。
水下发球管汇结构在发球过程中存在变形与振动的风险。一方面,水下发球管汇结构复杂,包含变径、弯头、三通等特征结构,压力场分布不均,易造成应力集中与结构变形[10-14];另一方面,发球过程中阀门的开关操作,向上游、下游传递增压波或减压波,导致管汇结构压力波动幅度大,管汇存在振动的风险[15-19]。因此,开展水下发球管汇的力学与振动分析研究,明确生产流体对管道结构的力学作用及其影响因素,掌握发球过程中水下发球管汇系统的振动特性,对于水下发球管汇系统的结构设计以及发球工艺的优化具有重要的指导作用。
目前,针对管汇系统的振动分析研究方法主要包括流固耦合模拟法[17-19],实验-模拟综合分析法[20-22]。流固耦合方法不断得到改进与完善,在管汇振动分析研究领域得到了长足的发展与验证,对多相流动工况的模拟计算较贴合实际[10],是掌握流体流动原因造成的管汇位移、应力集中以及振动规律重要途径之一。余成等[11]针对清管器发球装置在导流工况下的振动特性,建立了流固耦合数学模型,对输送介质为天然气和水分别进行了振动分析,结果表明:流固耦合条件下发球装置固有频率降低,说明管汇共振风险增大,而发球装置的固有频率在液固耦合下比气固耦合条件更低;振动剧烈位置主要为法连接处、旁通U型管处;壁厚、旁通直径与工作压力是固有频率的主要影响因素。于洋等[12]建立了管柱-钻井液-水泥浆流固耦合模型,采用有限元计算方法分析了管道长度、流体密度、环境温度对其固有频率影响,提出了利用强度大、低频率的激振力组合方式来增强固井质量的解决方案。张宇祥等[13]将计算流体力学与结构瞬态响应计算相结合,针对竖直弯管内气液两相流诱导振动的现象及规律进行了研究,结果表明:随着转弯角度的增大,气液两相流的流型转化加快,对弯头区域的冲击挤压作用以及管道的振动响应均呈现先增大后减小的趋势。李青等[14]研究了输油弯管在流固耦合作用下的模态,通过改变流体流速和压强,分析了流固耦合作用的管道的振动频率和应变,结果表明:流体流速的改变对振动频率的影响相对较小。Xu等[15]应用热-流-固耦合方法计算了不同工况下的流场压力和温度以及固体结构的温度、等效应力,比较了耦合载荷和非耦合载荷下管网和弯头受力特性。发现短臂锚固端部的最大等效应力位于其内壁,同一位置内壁等效应力大于外壁等效应力。Hamid等[16]通过建立用于计算流体动力学(computational fluid dynamics, CFD)分析的双向耦合流固相互作用(fluid solid interaction, FSI)框架,对常规和优化后管中管(PIP)系统的横向流动振荡进行了数值研究,发现采用弹簧和阻尼器来连接内外管道的PIP系统能显著降低涡激振动。祝效华等[20]针对双弯头管汇高压压裂过程,分析了流固耦合条件下连接角度、弯管的壁厚、曲率半径对固有频率的影响,结果表明双弯头连接角度影响较大,推荐为75°~105°;固有频率随弯管内径的增大呈似线性的增长。Zong等[22]应用流固耦合方法,结合实验和数值模拟,认为阀瓣净力过大以及阀瓣运动部件动能损失不足是造成压力容器-管道-安全阀系统不稳定运行的根本原因。
深水水下不停产清管仍然是一项世界性的深 水技术难题,为保障深水远距离清管作业安全实施, 应从设计、建造、运维等各阶段进一步加强水下清管的全流程的研究分析, 重点关注深水高压环境下的水下发球动态分析[7]。现针对某水下发球管汇,建立流固耦合数值模型,基于实际发球流程,开展内流场流体流动模拟计算,外场管汇结构力学分析,以掌握发球过程各时刻管汇结构的位移响应、应力分布以及振动特性,为深水水下不停产清管技术中发球管汇的结构设计、发球工艺的优化提供理论依据。
1 水下发球模块与数值模型
1.1 水下发球管汇模型与发球流程
某水下发球管汇结构及标识如图1所示,由30.48 cm的生产物流管道、15.24 cm的支管汇以及乙二醇(ethylene glycol, MEG)注入管汇组成,该发球管汇设置多个清管球发球通道,可实现一次发多个球,通过改变阀门的开闭状态,利用生产流体实现水下发球。正常生产流程为:生产物流流入30.48 cm管道,经过球阀“阀门1#”流入50.8 cm海底混输管道。完整的发球工艺流程如下。
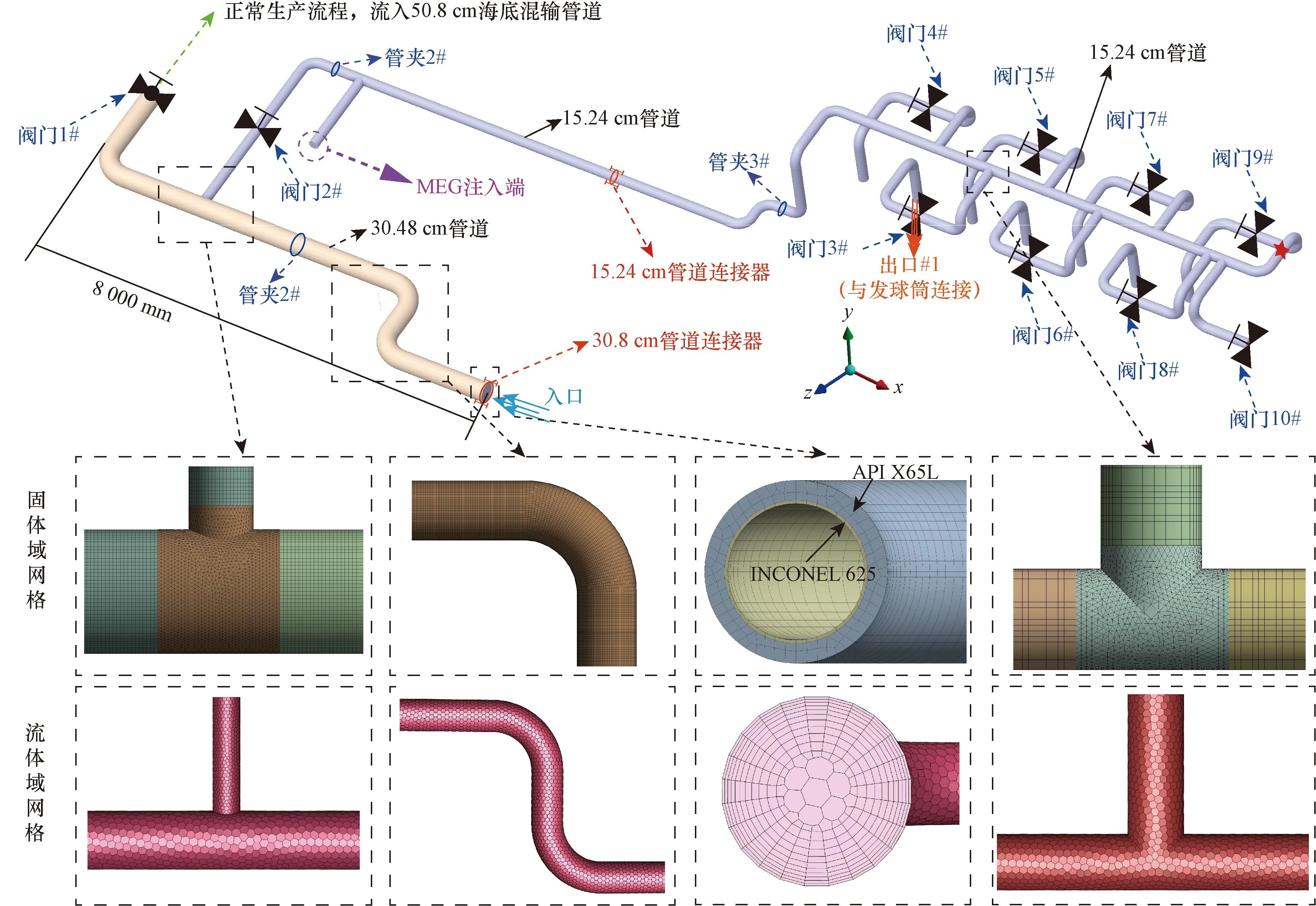
图1 发球管汇系统结构及网格划分结果Fig.1 Structure and meshing results of pigging manifold system
(1)准备发球阶段。降低部分生产井产量或关停部分生产井,将生产流体流量降低至发球流量(某典型发球工况流量为3×106m3/d)。
(2)准备发球阶段。打开球闸板阀“阀门2#”与闸板阀“阀门3#”,将30.48 cm物流管道与支管汇形成压力平衡。
(3)发球阶段。关闭球阀“阀门1#”,利用生产流体将清管球推出,实现清管作业。
(4)发球结束阶段。打开球阀“阀门1#”关闭闸板阀“阀门3#”与闸板阀“阀门2#”,并注入MEG,将支管汇内残存的生产流体进行置换,防止生产流体管汇产生腐蚀。
1.2 管壁结构与网格划分
为保证发球管汇的安全运行,考虑到生产流体的腐蚀性,管壁由3 mm具有优异防腐性能的内衬625合金与API X65L钢组成,管线规格参数如表1所示,API 5L X65 Q PSL2与INCONEL 625材料力学参数如表2所示。对水下发球管汇流体域部分进行网格划分,网格类型为多面体核心与六面体混合网格,如图1所示,共划分10层边界层,网格数量为1.16×106,最大偏斜度为0.69,网格质量较好。由于管壁结构存在3 mm的内衬625合金,内衬与管壁钢材之间的有机结合是建立计算模型及结果准确可靠的前提,应用六面体与四面体混合的网格类型。固体域网格划分结果如图1所示,异径T型管与各T型管处的网格连续性较高,弯管处网格连续,截面网格分布均一,钢材与内衬之间的连接无断点,网格正交质量绝大部分超过0.8,网格质量较好,网格数量为1.4×106。

表1 管线规格参数Table 1 Pipeline specification parameter
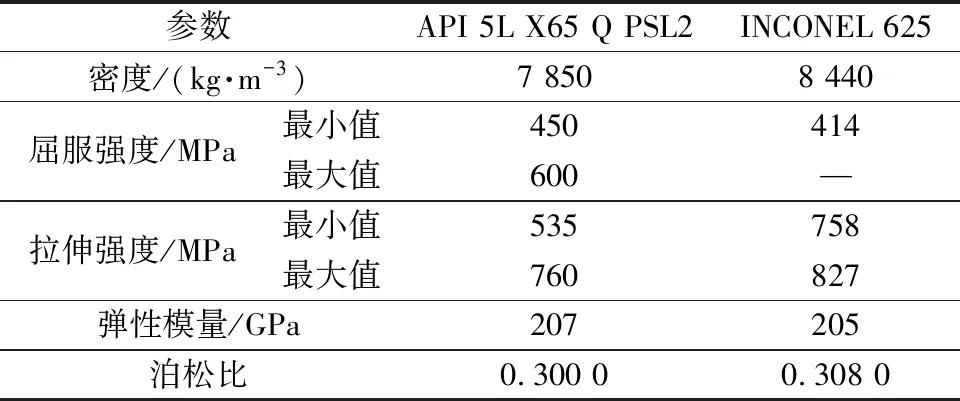
表2 管壁材料力学参数Table 2 Mechanical parameters of pipe wall material
2 计算方法与约束形式
2.1 计算方法
管内流体由气、油、水、MEG组成,各相物性参数如表3所示。流体计算部分,采用标准k-ε湍流模型(k为湍动能,ε为耗散率),近壁面区域采用标准壁面函数处理,采用VOF (volume of fluid)模型进行相界面的捕捉,采用Coupled算法对计算模型进行求解。其中,体积分数与体积力均采用隐式格式。针对流动方程中各项参数进行离散,压力采用PRESTO!离散格式、动量采用二阶迎风格式、湍动量及湍流耗散率均采用一阶迎风格式、体积分数采用隐式压缩格式。在瞬态流场计算过程中,为保证对流场变化的精确捕捉,时间步长取0.001~0.01 s,时间步采用一阶隐式格式进行离散。入口边界条件设置为速度入口3.74 m/s、出口边界条件设置为压力出口13.54 MPa。管壁结构部分,采用机械映射的方法将流体压力传导至固体壁面,考虑作用于管道外壁面的海水静压9 MPa,开展相关静力学及模态的计算与分析。
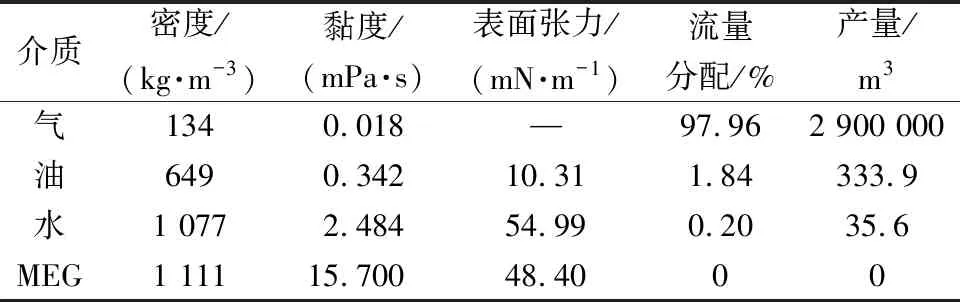
表3 典型工况运行参数及物性参数Table 3 Typical operating parameters and physical property parameters
2.2 约束形式
水下发球管汇系统支撑方案包含3种支撑形式:焊接(完全固定)、底部支撑(提供向上支撑)、管卡(限制径向自由度)。水下发球管汇约束形式及位置如图2所示,其中,完全固定位置为:30.48 cm管道连接器、15.24 cm管道连接器;终端(入口处、管汇与发球筒连接处、MEG注入端、阀门1#与阀门10#);向上支撑位置为:部分阀门处(阀门2#~9#);限制径向自由度位置为:管道沿线(管夹1#~3#)。
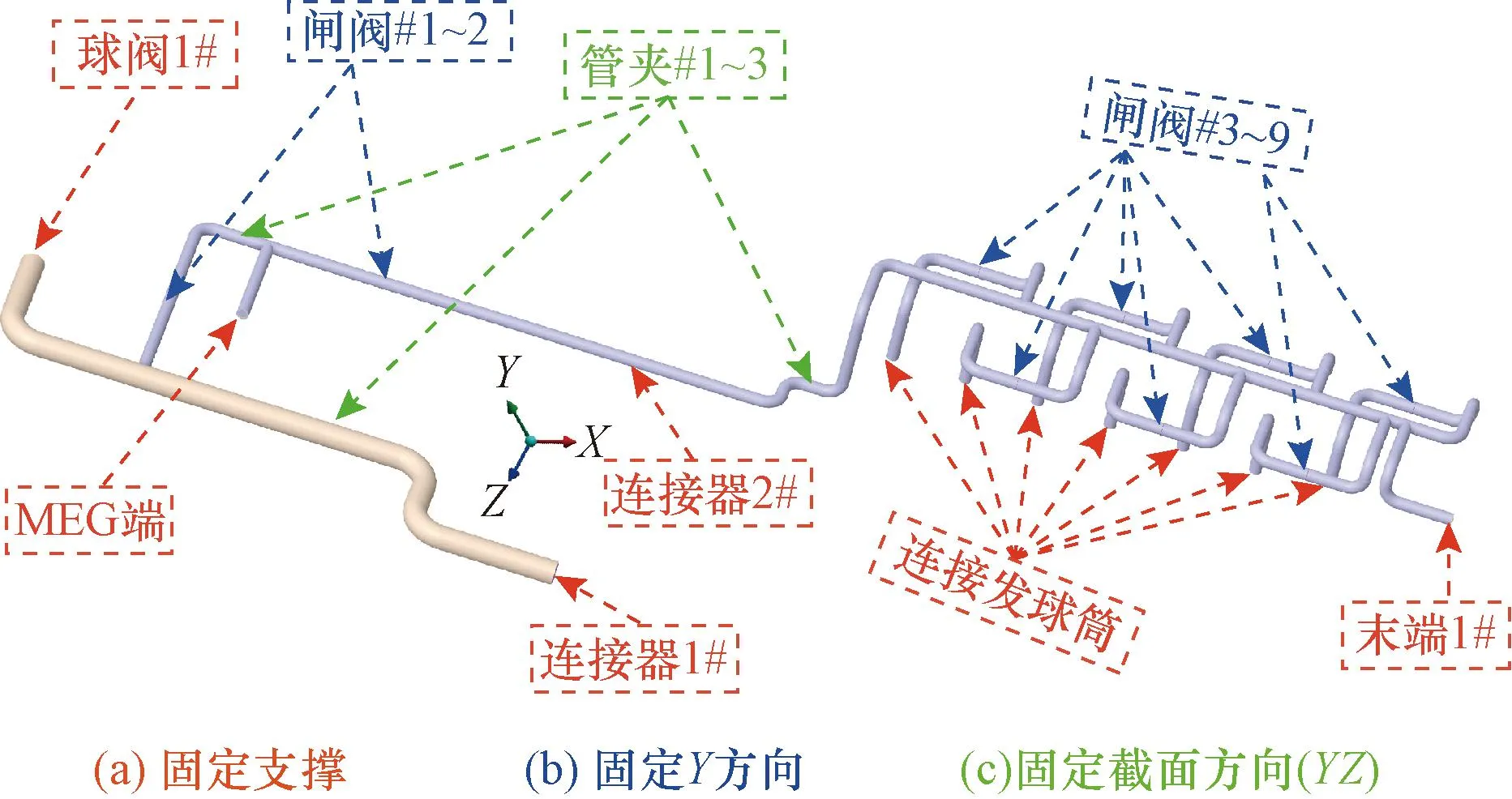
图2 水下发球管汇约束形式Fig.2 Underwater pigging manifold system constraint form
3 结果与分析
3.1 压力波动情况
为了准确模拟发球流程中管内流体流动状态,结合管汇结构的复杂性,将阀门的开闭设置为相应的边界条件(流通区域或固体区域),以贴合实际作。考虑阀门的开闭以及清管球的发出需要一定时间,将“发球前阶段”稳态计算结果作为瞬态计算的初始时刻(0 s);在“准备发球阶段”采用瞬态计算,共模拟60 s;在“发球阶段”瞬态计算,共模拟120 s。模拟计算获得发球流程中0、60、120 s时刻的气液两相分布,如图3所示。“0 s”时,生产流体经过30.48 cm管道流向50.8 cm海底集输管道,且此时15.24 cm支汇管内均被填充MEG;打开“阀门2#”,压力从30.48 cm管道传递至支汇管处,在此阶段在阀门2#后管道内正产流体与MEG之间存在动态置换,在“60 s时刻”MEG分布如图3(b)所示。关闭“阀门1#”生产流体全部从支汇管流出,推出清管球,共模拟120 s,在120 s时(中间时刻)支汇管内基本为生产流体,MEG分布状态如图3(c)所示。
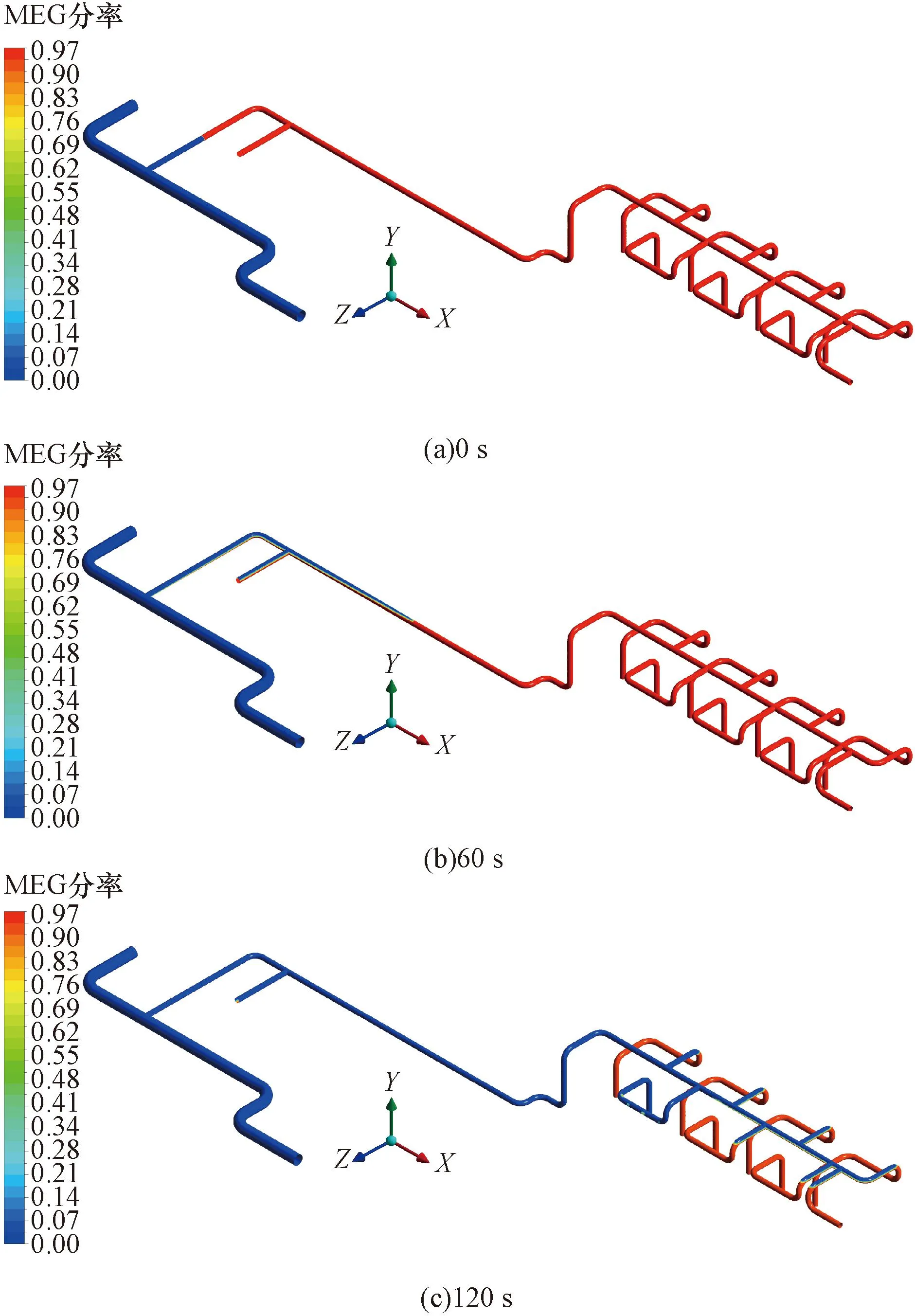
图3 发球过程中MEG在发球管汇结构内的占比Fig.3 Proportion of MEG in the pigging manifold during pigging
为掌握模拟过程中管汇内压力变化规律,提取模拟计算过程阀门2#与阀门3#位置中心处压力,获得管内压力变化的趋势,如图4所示。该位置压力在0 s之后约0.1 s压力波动幅度较大,最大压力出现在0~0.1 s和60~60.5 s,最大压力值约为17 MPa,在0.1~60 s和60.5~180 s压力保持稳定,且后一阶段压力略高于前一阶段,主要是由于管径变小、里程增大、弯管与T型管结构增多,管路摩阻增大。从压力波动趋势来看,阀门开关是压力变化幅度最大的特征时刻,也即引起管道位移、振动的特征时刻。
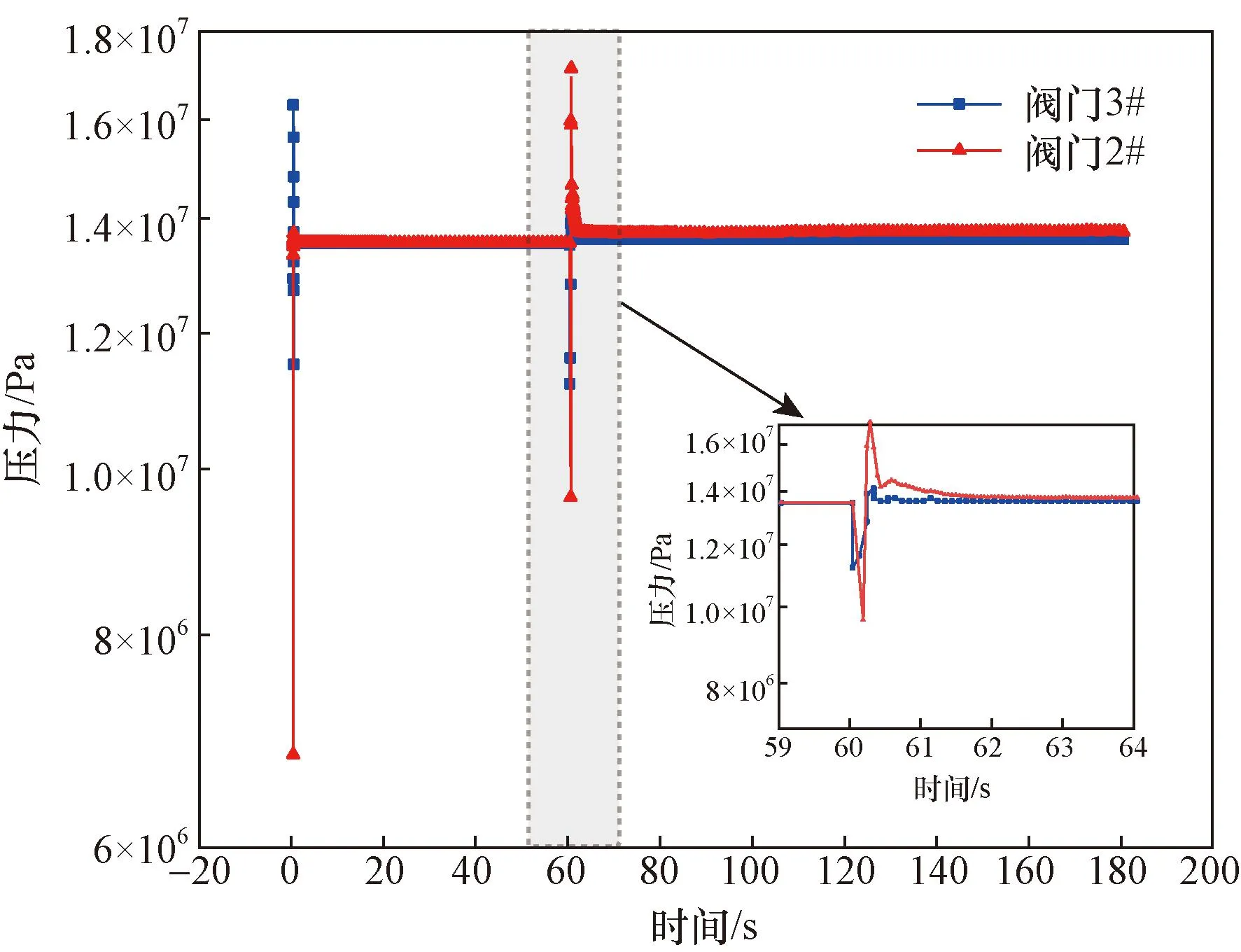
图4 阀门2#与3#位置处管道中心压力随时间的变化趋势Fig.4 Pressure trend over time at pipe center at valve # 2 and # 3
3.2 位移与等效应力分布
为反映发球过程中出现位移与应力情况,需提取特征压力时刻的压力场,进行流固耦合计算分析。提取了0.01、0.1、1、60、60.1、120、180 s的压力场作为内载荷,进行总变形、应力分布、应变分布的计算分析,计算结果如表4所示,0.01 s时刻总位移及X、Y、Z方向位移如图5所示,等效应力分布如图6所示。在0.01 s与60.1 s时刻的流场压力作用下,管汇结构最大位移分别达到5.28、5.69 mm,分布在管汇结构的末端,这两个时刻属于管汇出现压力波动的时期,存在局部高压,使得管道结构在末端存在一定程度的位移。在发球过程中其他平稳阶段的时刻压力场的作用下的最大位移非常小,在1、60、120、180 s时刻的流场压力作用下,其管汇最大位移为0.058、0.058、0.21、0.25 mm,出现在管汇前端和末端,相对比较安全。
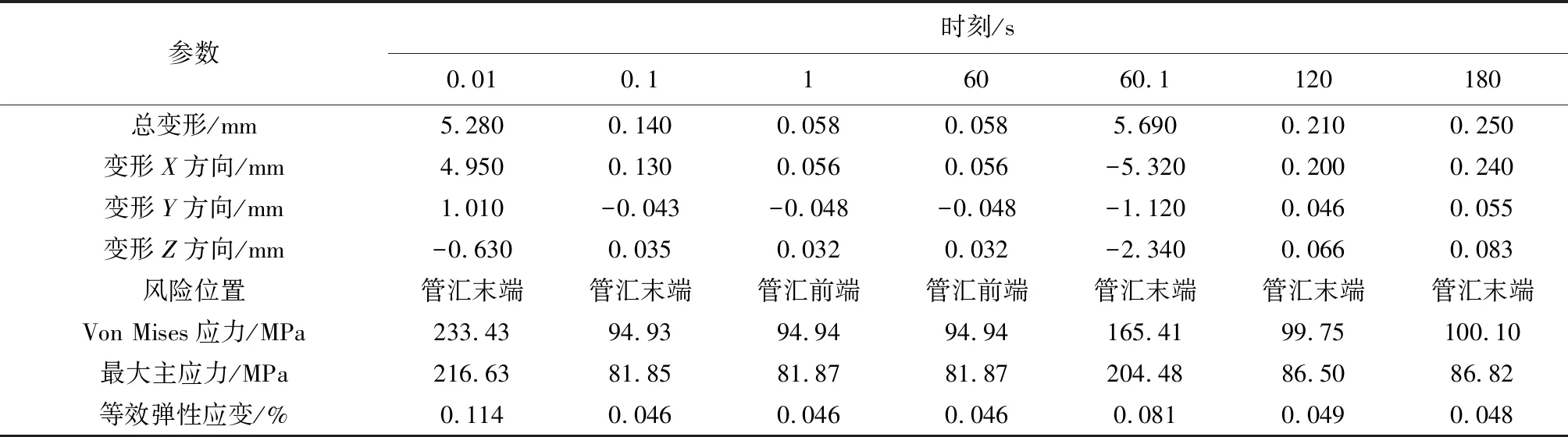
表4 发球流程中各特征时刻静力学计算分析结果Table 4 Results of statics calculation and analysis of each characteristic moment in pigging process
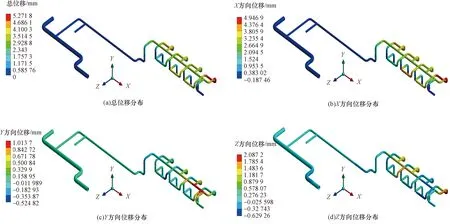
图5 0.01 s时刻发球管汇位移分布Fig.5 Displacement distribution at 0.01 s
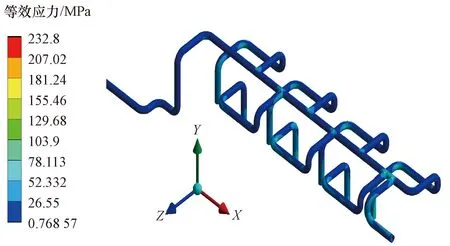
图6 0.01 s时刻发球管汇等效应力分布Fig.6 Distribution of equivalent effect force at 0.01 s
对比管汇结构在X、Y、Z方向的位移贡献,发现管汇最大位移主要由管汇末端结构的X方向位移提供,可考虑在管汇结构末端施加X方向的位移约束。最大等效应力、最大主应力及最大等效应变主要出现在T型管处及弯管内侧,主要原因是在T型管处流速分布非常不均,在弯管处内侧压力要高于外侧压力,与文献[12]的研究结果一致。0.01 s时刻流场压力作用下的等效应力最大,可达233.43 MPa,最大主应力可达216.63 MPa,但相比于最小屈服强度(450 MPa)更低,在安全设计系数下,管道符合强度准则要求。0.01 s时刻流场压力作用下的等效应变最大,可达0.114%,其他时刻为0.04%~0.08%,应变程度较小,管道符合安全强度评价标准。
3.3 模态频率
基于静力学分析结果,可以看出管汇末端处是风险位点,而管道约束方案对模态频率及振型的影响幅度较为明显。进行管汇结构支撑方案优化:在管汇末端支管增加一个管夹,限制径向自由度,即限制X、Y方向位移,如图1中红星处所示。在新支撑方案下,管汇结构0.01 s时刻压力作用下管汇最大位移降低至3.53 mm,出现在管汇前端支管处。最大等效应力降低至204.97 MPa,最大主应力降低至187.88 MPa,最大等效应变降低至0.1%,说明增加管夹后管道的安全性得到了提高。
优化支撑方案与原始支撑方案下管汇结构的模态振型及振动频率变化对比如图7所示。对比来看,添加管夹前后管汇的1阶与3阶振型基本不变,2阶、4阶、5阶、6阶振型存在差异。1~6阶振动频率均有一定程度的提高(图8),增幅为1.74%~20.54%。文献[20]中提到物理结构的低阶频率越低,结构频率易与环境频率(如海浪冲击频率)重合,将会导致管道产生共振现象,严重危害结构安全,优化支撑方案管汇结构低阶频率的提高也间接说明管道在水下发生共振的概率更低。

图7 原始支撑方案与优化支撑方案1~6阶模态振型图Fig.7 Original support scheme and optimized support scheme 1~6 mode shapes
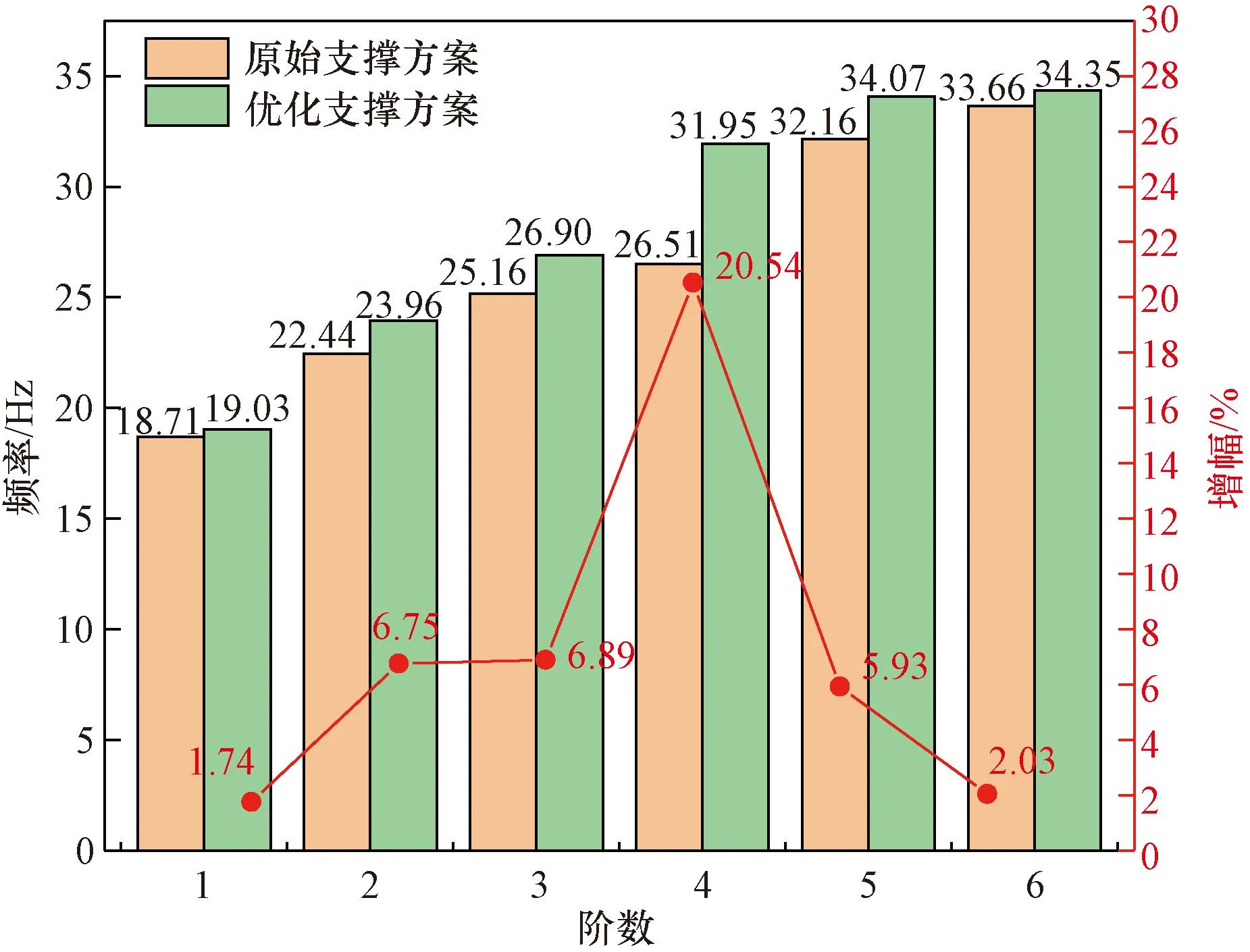
图8 原始支撑方案与优化支撑方案1~6阶模态频率及对比增幅Fig.8 Comparison of the mode frequency of order 1~6 of the original support scheme and the optimized support scheme
4 结论
(1)基于流场压力的模拟计算,获得了发球管汇在发球过程管内压力随时间的变化趋势,发现阀门开关是压力变化幅度最大的特征时刻,也即引起管道位移、振动的特征时刻,需重点关注瞬态压力对管道结构的冲击影响。
(2)通过分析水下发球管汇发球流程中流体压力造成的管汇结构位移、应力分布,明确了管道结构风险位点为管汇结构末端,最大位移为5.69 mm,主要由X方向贡献,最大等效应力为233.13 MPa,主要集中分布在T型管、弯管内侧处。
(3)提出了针对性的优化支撑方案,管汇结构最大位移降低至3.53 mm,模态频率增幅约为1.74%~20.54%,管汇结构的安全性得到了提高,水下发球管汇的安全性。
水下发球管汇的力学特性及振动分析结果,指明了水下发球管会的风险位置以及优化措施,可为水下发球管汇的设计与优化提供理论指导以及方法参考,助力深水水下不停产清管技术的发展。还需进一步与室内模拟实验研究结合,以期达到更加贴合实际的数值模拟效果。
