基于数字孪生的水土流失防治责任范围变化预测模型

卢敬德 ，李智广

（1. 广东无限阵列科技有限公司，广东 广州 510055；2. 水利部水土保持监测中心，北京 100055）

0 引言

当前，水利部按照“需求牵引、应用至上、数字赋能、提升能力”的要求，正在加快推进智慧水利建设。数字孪生技术可实现数字模型与物理实体同步仿真运行、虚实交互、迭代优化，对加快构建具有预报、预警、预演、预案功能的智慧水利体系发挥着基础性作用[1-3]。在智慧水土保持建设中，不断加大监管信息化程度，实现了全国水土保持遥感监管全覆盖，认定和查处了未批先建、未批先弃、超出防治责任范围等违法违规项目，推进了水土保持方案编报率、违规整改到位率和设施验收率连年提升，对有效防止人为水土流失、保护和改善生态环境发挥了良好作用[4-5]。但将生产建设项目水土流失防治责任范围这一具有显著动态变化特性的事物当作静态对象认识，常常导致一些水土保持违法违规活动不能被及时识别和认定，造成遥感监管盲点。

姜德文等[6-9]通过 GIS 技术，梳理了扰动图斑与防治责任范围的空间逻辑关系，提出将遥感监管发现的扰动图斑与防治责任范围进行空间叠加分析，判别生产建设项目程序合规性的方法。但将以往入库、未被及时更新、未能同步孪生的防治责任范围，与现势性更高、更具时效性的扰动图斑叠加，必然难以生成符合现状的生产建设活动合规性判别结果。李智广等[10]首次提出利用数字孪生技术建立防治责任范围变化的预测方法，为减少违法违规活动的漏判和误判提供了新的思路。

本研究系统梳理和归纳水土流失防治责任范围的动态特性，结合数字孪生技术，构建水土流失防治责任范围变化预测模型，并进行应用试验和效果分析。

1 防治责任范围动态变化特性

GB 50433—2018《生产建设项目水土保持技术标准》规定，防治责任范围是指生产建设单位依法承担水土流失防治义务的区域，包括项目永久占地、临时占地（含租赁土地）及其他使用和管辖区域。防治责任范围既具有鲜明的空间确定特性，又具有鲜明的动态变化特性。空间确定特性是指在一定时段内，防治责任范围既具有确定的空间位置又具有确定的空间范围的特性，要求项目的建设和生产不得随意改变防治责任范围的位置、超出防治责任范围的界线，为遥感监管识别和认定生产建设活动的合规性提供了基础。为做好生产建设项目水土保持监管工作（包括遥感监管），应采用先进技术及时更新、生成高现势性的防治责任范围。动态变化特性是指在生产建设项目的全生命周期中，防治责任范围随着项目建设与生产等活动变化而变化的特性，主要表现在可撤销性、时空交错性、临时性、适用条件失效性等 4 个方面。

1.1 可撤销性

防治责任范围的可撤销性是指审批机关对存在严重质量问题的水土保持方案撤回水土保持方案审批准予行政许可，使得防治责任范围失去效力的特性。

水土保持方案审批准予行政许可被撤销示例如图1 所示，该项目由于水土保持措施体系不完整，存在明显缺陷，施工营区未进行边坡防护，高边坡防护区主体已有永久截排水措施未列入防治措施体系，而被依法撤销水土保持方案审批准予行政许可，其中，图 a 和 b 分别反映的是水土保持方案审批准予行政许可撤销前、后的水土流失防治责任范围的变化情况。

图1 水土保持方案审批准予行政许可被撤销示例

1.2 时空交错性

防治责任范围的时空交错性是指不同时期的生产建设项目共用了一个防治责任范围或其中一部分，使得同一防治责任范围内存在不同项目的特性。若在同一地理范围出现不同项目防治责任范围时空交错，很可能导致遥感监管时把未批先建的扰动图斑误判为“合规”，具体示例如图2 所示，其中红线为防治责任范围，黄线为扰动图斑。

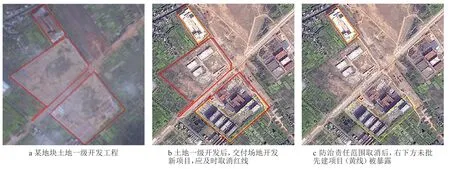
图2 防治责任范围时空交错性导致合规性误判示例

1.3 临时性

防治责任范围的临时性是指防治责任范围包含临时占地，在项目建设完工后，临时占地被归还、不再属于项目占地范围、并可被新项目征占的特性，具体示例如图3 所示，图 a 中的 3 个红边淡黄色半透明填充地块为某项目建设期间的临时占地；图 b 中黄线框内为该项目建成后临时用地流转为另一项目的建设用地，此时该黄线框内地块属于新增扰动。

图3 临时用地流转导致防治责任范围变化示例

1.4 适用条件失效性

经批准后的水土保持方案或依法免予办理水土保持方案审批手续的项目，由于性质、选址地点、规模等发生重大变化，应编报水土保持方案或进行变更。这些情形导致原来的法律法规条款不再适用，水土保持方案审批准予行政许可不再匹配，导致防治责任范围有效性发生变化的特性称为适用条件失效性。

近年来，政府推行在开发区统一编制水土保持区域评估报告的政策，评估结果对开发区内全部项目共享。为切实做好水土保持监管工作，水行政主管部门对水土保持区域评估适用性提出一定要求，如广东省自然资源厅等 7 个部门出台《关于印发广东省工程建设项目区域评估操作规程的函》（粤自然资函〔2019〕2284 号），规定单个项目征占地超过 20 hm2或挖填方总量超过 2×105m3时，应单独编报水土保持方案，具体示例如图4 所示，图 a 中红边淡紫色填充区为某水土保持区域评估区；图 b 中淡黄色填充区每个项目占地面积均大于 20 hm2，因此评估区范围内项目可免于单独编报水土保持方案的适用条件失效。

图4 适用条件失效性导致防治责任范围变化示例

2 防治责任范围变化预测模型

2.1 构建思路

在全面掌握项目基本属性与发展情况的基础上，深入研究导致防治责任范围变化的主要事件与概率，构建防治责任范围变化预测模型，将现实中项目防治责任范围发生的变化同步映射到虚拟的数字孪生对象上，当数字孪生的防治责任范围对象失效概率达到设定阈值时，模型发出警告信号，提示工作人员及时检查、更新防治责任范围，并同步孪生形成新的防治责任范围。

根据数字孪生的基本原理，可将遥感监管的应用情景理解为：防治责任范围为物理实体，数学模型为描述防治责任范围状态的虚拟模型，模型基于防治责任范围发生变化主要因素的孪生数据，对防治责任范围有效性状态进行评估和预测，从而形成从物理水土流失防治责任范围到孪生数据，最后映射至数学模型的闭环。

2.2 构建方法

按照 4 个动态变化特性，对引起防治责任范围变化的情形进行归纳，形成动态特性-影响因素-分布特征关系，变化情形如图5 所示。根据 4 个动态变化特性的主要分布，建立合适的概率公式，得到防治责任范围变化预测模型，各类事件发生概率如下：

图5 引起防治责任范围变化情形结构图

1） 防治责任范围变化事件发生概率。防治责任范围是否变化由可撤销性、时空交错性、临时性、适用条件失效性等 4 个方面决定。根据乘法原理，概率计算公式为

式中：P（A）为防治责任范围变化事件A发生的概率；P（R），P（S），P（T），P（Q）分别为项目发生水土保持方案审批准予行政许可被撤销事件R、时空交错事件S、临时用地变化事件T、适用条件失效事件Q的概率。

2） 撤销水土保持方案审批准予行政许可事件概率，与项目被抽中进行水土保持方案质量核查的概率和水土保持方案编报的质量 2 个因素有关。从抽查角度，水土保持方案编报质量好坏为随机事件；项目是否被抽中进行水土保持方案质量核查，与建设单位或方案编制单位是否曾被列入重点关注名单（事件W）、黑名单（事件B）（信用监管“两单”）[11]、曾被撤销水土保持方案审批准予行政许可（事件L）、曾被约谈（事件I）等 4 种信用记录有关。概率计算公式为

式中：r∈[0，1），为模型控制变量，可设定为历史累计撤销水土保持方案审批准予行政许可次数与历史累计审批准予许可总数的比值。P（W），P（B），P（L），P（I）分别为项目因市场主体存在 4 类不良信用记录而被抽中进行水土保持方案质量核查的概率，计算公式如下：

式中：v1（p），v2（p），v3（p），v4（p）分别为计算机判断函数，用于判断项目p有关市场主体存在 4 类不良信用记录的情形，当事件发生时返回数值 1，否则返回数值 0；w，b，l，i的取值均为[0，1]，均为模型控制变量，分别表示项目有关市场主体存在 4 类不良信用记录时，被抽中的敏感程度，可根据不同行政区对此事件的敏感程度设定数值，数值越大，被抽中概率越高。

3） 时空交错事件概率。在时空交错事件概率P（S）建模时，计算公式遵循收集、整理样本数据—回归分析—拟合算式—验算的推导过程。

收集我国大湾区 C 市 2018 年 7 月 1 日至 2022 年7 月 31 日水土保持方案数据，对土地一级开发类项目完工与防治责任范围内是否发生时空交错事件进行分析。将完工时长按照完工后 2，4，6，…，48 个月划分为 24 个区间，统计每个区间内该类项目完工后原防治责任范围内产生新项目的比例，通过回归分析确定项目完工时长区间与时空交错事件发生比例之间的统计关系如图6 所示。

图6 土地一级开发类项目完工时间与防治责任范围内发生时空交错事件的统计关系

图6 表明：在 40～48（水平轴读数 20～24）个月时长区间，曲线几乎平行于水平轴，说明在同一地块上，无论建设完工了哪种项目，在完工后 48 个月内，如果该地块没有出现新的项目，后续该地块再出现新项目的概率很低（接近于 0）。本研究将正态分布公式中e的指数的分子取倒数，样本的统计曲线与正态分布曲线拟合程度较好，因此可得到时空交错事件发生概率P（S）计算公式如下：

式中：v5（p）为计算机判断函数，当项目p属于土地一级开发类项目时，返回数值 1，否则返回数值 0；P（PD）为土地一级开发工程完工后防治责任范围内产生新项目事件的概率，计算公式为

式中：σ1为模型参数，代表事件PD分布的离散程度，决定特征曲线收敛的速度，根据应用区域经济活跃程度确定取值，活跃程度越高取值越大，默认值一般为 2；tc为当前时间；t1为计划完工时间；g（t）为线性归一化函数，作用是将有量纲的时间变换为值域在（0，1]的无量纲数。

4） 临时用地变化事件概率。临时用地变化事件发生概率P（T）与时空交错事件发生概率类似，计算公式为

式中：v6（p）为计算机判断函数，当项目p包含临时占地时，返回数值 1，否则返回数值 0；P（TD）为包含临时用地项目完工后原防治责任范围内的临时用地流转到新项目事件的概率，计算公式为

式中：σ2为事件TD分布的离散程度。

5） 适用条件失效事件概率。以项目p为中心，生成n个适当扩大范围的分析区，计算分析区内所有扰动图斑的占地面积之和与分析区总面积之比，比值越大，说明项目p附近同源扰动越多，适用条件失效事件概率越高。适用条件失效事件概率P（Q）的计算公式为

式中：v7（p）为计算机判断函数，当项目p位于开展区域评估的区域时，返回数值 1，否则返回数值 0；Ac为项目p可免予单独审批水土保持方案的占地面积值；Ai为当前项目p的扰动面积；为以项目p为中心，面积为Ac·q的缓冲区内所有扰动图斑的占地面积之和，q∈（1，9]，为外扩比例，通常采用以当前项目p为中心的正九宫格外扩方式产生分析区，此时q取值为 9。

3 试验结果分析

3.1 试验结果

在我国大湾区 C 市进行试验，将构建的防治责任范围变化预测模型嵌入遥感监管系统，并将全市自2018 年以来获得水土保持方案准予决定的 1 182 个项目相关数据录入系统，数据相关内容如表1 所示。

模型参数σ1设定为 5；线性项目（共 89 个）σ2设为 1，其他项目σ2设定为 2；w设定为 0.6，b设定为0.3，l设定为 0.2，i设定为 0.1，系统对防治责任范围是否失效作出判断的界限值，即阈值设定为 0.6。计算得到每个项目防治责任范围失效的概率，当计算结果大于设定的阈值时，将该项目警告标志位设为“True”，即从系统角度判断该项目防治责任范围已失效。随后核实系统判断项目防治责任范围失效的实际情况，确定失效的即为命中，统计结果如表2 所示。

表2 模型试验计算结果分类统计

3.2 结果分析

由表2 可知，模型将 298 个项目的警告标志位设为“True”，占项目总数的 25.21%。经实际调查发现，其中防治责任范围实际发生变化的项目共 113 个，占警告总数的 37.92%。通过系统输出每一个被警告项目的原因，分析触发警告的主导影响因素、警告数量、实际变化数量等，进行模型计算正确性分析。结果分析如下：

1） 模型对发生撤销水土保持方案审批准予行政许可事件R预测的命中率偏低，仅为 12.5%，主要原因是C 市从 2020 年 7 月 24 日才开始实行信用监管“两单”制度，且撤销水土保持方案审批准予行政许可的样本发生在制度实行 1 年之后，目前尚未形成足够多的样本。

2） 模型对发生时空交错事件S预测的命中率为45.5%，主要原因是试验时大多数项目在 48 个月之内完工，时间较短，原防治责任范围内还未有新项目入住。但随着时间推移，当新项目入驻、开始施工时，时空交错事件将更多，命中率会明显提升。

3） 模型对发生临时用地变化事件T预测的命中率为 43.1%，主要原因是试验时大多数项目在 48 个月之内完工，临时用地还未发生流转。但随着时间推移，临时用地流转成为新项目用地的事件将继续发生，命中率会有所提升。

4） 模型对发生适用条件失效事件Q预测的命中率为 66.7%，在 4 个分项中最高，原因可能是试验区为国家级新区，规划和开发的边界比较明晰，与反距离权重法的原理契合度较高。

当前，水土流失防治责任范围伴随水土保持方案审批准予行政许可的获得而生效，且在一般情况下，不会主动分析水土流失防治责任范围是否失效。本研究提出的模型能主动判断并命中其中已失效的防治责任范围，从而减少或避免遥感监管的漏判和误判，提升遥感监管成果的应用价值。

4 结语

针对水土流失防治责任范围变化导致遥感监管对违法违规活动漏判和误判的现象，基于数字孪生的水土流失防治责任范围变化预测模型，经大数据试验得到了良好的预测效果。研究成果如下：

1） 导致防治责任范围变化的因素主要包括可撤销性、时空交错性、临时性和适用条件失效性等。在遥感监管中，应及时孪生形成高现势性的防治责任范围，有效提高遥感监管识别违法违规活动的正确率，保证监管成果的质量。

2） 模型对试验区可撤销性引发防治变化预测的命中率偏低，但随着水土保持方案质量抽查及其他监管措施的进一步落实，模型预测命中率会有所提升。

3） 本试验区适用条件失效概率预测的命中率较高，主要原因是试验区规划和开发边界比较明晰。由于此项概率计算的正确性对空间统计方法的选取比较敏感，可根据不同性质的区域评估对象，选取合适的空间统计方法。

为达到更理想的效果，在未来的工作中，应进一步研究和优化防治责任范围动态变化数字孪生模型，严格甄别可撤销性、临时性涉及的各种情形，调整和增加与防治责任范围关联度更为密切的情形，并进一步提高模型基于水土保持信用数据进行预测的稳健性。