基于算法归因框架的专利维持时间影响因素探究
2024-02-28付振康柳炳祥鄢春根周子钰宫秀燕
付振康 柳炳祥 鄢春根 周子钰 宫秀燕
(1.南京大学信息管理学院,南京,210023; 2.景德镇陶瓷大学信息工程学院,景德镇,333403; 3.景德镇陶瓷大学知识产权信息中心,景德镇,333403; 4.黑龙江八一农垦大学经济管理学院,大庆,163316)
1 引言
专利维持时间(patent maintenance time)又称专利寿命(patent lifespan),指专利自申请日至专利失效日所经历的时间[1],目前专利维持时间被公认为可以作为专利质量或专利价值的衡量指标[1-5]。然而,专利维持时间虽然能够较好地反映专利价值,但是也存在严重的滞后性[3],即维持时间需要在专利权终止或者期限届满时才能确定,而在此时评价专利质量或专利价值已经毫无意义。目前,理论界和实务界在使用专利维持时间时,往往是通过设定阈值来判断专利的价值,例如,邓洁等将维持时间大于6.6年的专利定义为高质量专利[4],国家知识产权局将维持时间在10年以上的发明专利定义为高价值专利[5],但即使设定阈值,采用维持时间来测度专利价值也至少需要6年时间。
在专利申请或者授权前期,如果能对专利未来的维持状况进行一定程度的预见,将对专利价值评估、专利质押融资和专利成果转化等工作具有十分重要的意义。在数智时代,结合大数据和智能算法对专利维持时间进行预测,在一定程度上可以解决专利维持时间在实际应用过程中的滞后性问题。但是,对专利维持时间进行精准预测的前提是要在繁杂的数据中找到与专利维持时间密切相关的因素,然后才能建立相关的预测模型进行预测。在专利大数据背景下,哪些因素会影响专利维持时间,以及采用何种方法能够准确且全面地测度不同因素对专利维持时间的影响效应大小等问题,是实现专利维持时间精准预测亟待解决的问题。
因此,本文以2001—2017年中国国家知识产权局授权的50余万件专利作为研究样本,从可解释性机器学习的视角出发,构建基于生存分析的机器学习算法归因框架,探究不同因素对专利维持时间的作用大小,并分析不同因素在不同专利文献生命周期阶段影响效应的变化情况。在理论层面,本研究可以为专利维持时间影响因素分析及维持时间预测提供新的研究视角及研究模型;在实践层面,本研究可以为专利价值评估和企业专利维持决策提供较为准确的指标体系。
2 相关研究
国内外关于专利维持时间影响因素的实证研究旨在刻画不同因素与专利维持时间之间的关联关系,研究领域多集中在情报学、科技政策和技术创新管理等领域。
在情报学视域下,研究者多从文献计量的视角探究不同专利文献计量指标和专利维持时间之间的关联关系。例如,Bessen[6]的研究表明,后向引证频次与专利维持之间存在正相关性,但相关性程度较弱,这类正相关性在Harhoff等[7]、Hikkerova等[8]和Gam-bardella等[9]的研究中同样得到证明。李睿等[10]同样发现专利后向引证频次与专利维持时间之间存在显著正相关性,但不同的引证类别与专利维持时间之间的相关性强弱有所差异;而胡成等[11]研究表明后向引证频次与专利维持时间之间呈现弱负相关关系。除专利的引证指标外,部分学者也对专利的权利要求数量、文献篇幅、首权字数、专利家族规模和技术覆盖范围等指标与专利维持时间之间的关系进行了探究。乔永忠[12-13]研究表明,发明人数量对专利维持时间具有显著正向影响,审查周期对专利维持时间具有显著的负向影响,权利要求数量对专利维持时间的影响因专利公开国别的不同而存在异质性;Lee[14]发现权利要求数量对专利维持时间具有显著的正向影响,而发明人数量对专利维持时间的影响并不显著;吴红等[15]指出,权利要求数量以及专利家族规模对中国发明专利维持时间具有显著正向影响,而日本发明专利维持时间仅受发明人数量的显著正向影响;而刘雪凤等[16]则发现,发明人数量对专利维持时间具有负向影响,权利要求数量以及专利家族规模对专利维持时间具有显著的正向影响;肖冰[17]认为权利要求数量以及审查周期对专利维持时间具有显著正向影响,而发明人数量和同族专利数量对专利维持时间的影响效应并不显著;冯仁涛[18]实证了首权字数、权利要求数量、发明人数量以及合作开发均正向影响专利维持时间,而专利审查周期以及技术覆盖范围对专利维持时间具有负向影响,首权字数对专利维持时间的影响效应受文献篇幅的调节。
在科技政策和技术创新管理的研究视域下,研究者多数关注的是创新政策环境、技术市场环境、技术扩散和专利年费制度等经济社会环境对专利维持的影响。毛昊等[19]研究表明,规模较大企业的专利维持受政策环境的影响较大,而专利管理水平较高、自评专利质量较高的企业的专利维持主要受市场环境驱动;张军荣等[20]研究发现,中国“拜杜法案”的实施并未显著地提升高校和科研机构的专利维持时间;Jang等[21]发现,企业的专利存量对专利维持具有非线性影响效应,企业盈利能力、企业规模和行业内年均销售增长速率对专利维持时间具有正向影响,而企业年龄对企业专利维持具有负向影响效应;李兰花等[22]对我国“211高校”的专利维持时间的实证研究表明,专利商业化时间和市场不确定性对高校专利维持时间具有正向影响,而市场供给竞争强度对高校的专利维持时间具有负向影响;Lee等[23]研究表明,专利技术的社会扩散度和功能多元性对专利维持时间具有显著影响;乔永忠[24]认为专利年费制度对专利维持具有显著影响,且在不同国家和不同时期的影响效应不同。
通过梳理相关文献发现,国内外学者虽然就专利维持时间的影响因素开展了相应研究,但是相关研究依然存在进一步深化的空间:①在研究方法方面,多采用线性模型对影响因素的效应大小进行估计,不能有效地刻画各因素之间的非线性关系;②在影响因素的选取方面,研究者多是从专利价值或专利质量的视角选取影响专利维持时间的因素,较少有研究从专利维持时间自身出发,系统归纳和整理影响专利维持的主要因素;③在样本数据方面,多是以特定技术领域或特定时间内的专利数据作为样本,研究结果会出现选择性偏误,导致不同研究结果的差异较大;④在实证研究方面,多是探索各因素与维持时间之间的静态关系,较少探索各因素和维持时间之间的动态关系。
鉴于此,本文以2001—2017年间在中国国家知识产权局申请并获得授权的510614件发明专利作为样本,基于生物学理论视角归纳影响专利维持时间的因素,同时构建融合生存分析的可解释性机器学习算法归因框架,分析影响专利维持时间的各因素作用大小,同时分析不同技术领域和不同时间段内影响因素作用的变化情况。
3 研究设计与方法
3.1 问题定义
专利生命周期包括申请、授权和失效(包括未缴年费、无效宣告、诉讼无效和期限届满)三种状态,这类似于“生命体”的孕育、出生和消亡,很多学者也认为专利维持时间数据是一种典型的生存数据,即无论将数据采集的截止时间定于何时,都会有一些专利已经失效,而另一些专利依然在维持当中,因此专利维持时间数据存在大量的右截尾数据[15,22,25-29]。基于此,本文将专利维持时间的分析或者预测定义为一个生存分析问题,在研究过程中使用生存分析方法进行模型构建和归因分析。
3.2 研究框架与研究流程
算法归因也称数据驱动归因(data-driven attribution),该方法常用于用户价值细分、线上线下的营销分析当中。算法归因需要以机器学习模型作为基准模型,对变量间的潜在模式和量化关系进行挖掘。虽然机器学习算法在大规模复杂数据之间潜在关联模式挖掘和预测方面体现出了其独特的优势,但是作为“黑盒模型”,其无法解释的预测过程也使其在应用过程中受到一定质疑。在专利维持时间的预测过程中,决策者不仅需要精准的预测结果,也需要具体的逻辑判断过程。因此,本文结合可解释机器学习方法,构建了如图1所示的算法归因框架,从大规模专利数据中挖掘影响专利维持时间的潜在因素及其关系模式,为专利维持时间的相关研究提供新的研究视角和研究方法。
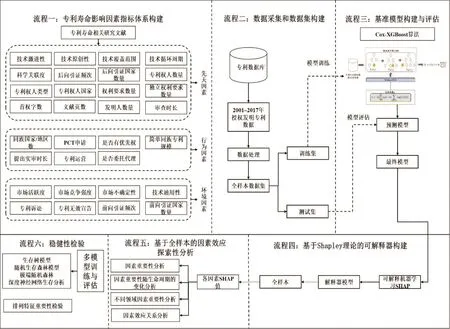
图1 算法归因框架
3.2.1 专利维持时间影响因素指标体系构建
根据生物学理论,可以将影响人类寿命的因素划分为“先天因素”和“后天因素”,“后天因素”又可以分为“行为因素”和“环境因素”,因此本文依照该理论,将影响专利维持时间的因素划分为三个维度,其中“先天因素”代表专利文献自身的因素,“行为因素”代表专利权人后期对相关专利的运营等行为,“环境因素”代表专利技术所处行业的市场环境等[29]。有学者认为,医疗水平和经济环境等“后天因素”对人类寿命的影响更大,“后天因素”决定了70%至80%的寿命[30-31]。但本文认为在专利生命周期当中,“先天因素”对专利维持的影响更大,因为专利技术的创新性和专利的法律保护范围会直接影响专利权人的维持行为。结合前人研究,表1归纳总结了影响专利维持时间的31项主要因素。

表1 专利维持时间影响因素指标体系
3.2.2 基准预测模型构建与评估
与传统的统计学归因方法不同,算法归因是通过机器学习预测模型,对数据间的潜在模式和量化关系进行刻画,机器学习模型的选择会直接影响不同特征之间关系的量化结果[36-37]。本文使用XGBoost算法构建生存预测模型,引入XGBoost算法的原因主要包括以下三个方面:①XGBoost算法是基于Boosting思想的基础算法,通过添加正则化项提高模型的泛化能力,采用二阶导数的方式提升模型的精准性,进而使预测结果更加准确,同时防止出现过拟合现象;②本文专利维持时间影响因素共包括31个自变量,这使得特征集数据较为复杂,而传统的Cox模型是风险比例半参数模型,需要较强的在先假设,因此在中高维复杂数据集上的表现较差,而XGBoost算法在中高维数据集上具有良好的训练速度和预测精度,可以提升专利维持时间影响因素分析的准确性及效率;③XGBoost算法采用决策树对基学习器进行优化,这使得XGBoost算法具有较高的可解释性,这一特性对于准确量化分析不同因素对专利维持时间的影响效应,建立稳健的算法归因框架至关重要。
本文构建的Cox-XGBoost模型是一种特殊的回归模型,其原理与传统XGBoost机器学习回归模型一致,即通过梯度提升算法和正则化项来构建一个性能更好的预测模型,在此不再赘述。值得注意的是Cox-XGBoost模型的输出为每件专利的对数风险函数值,并非每件专利的实际存活时间,这与生存分析的原理是一致的。
在模型评估过程中,采用生存分析常用的一致性指数(Concordance Index,CI)[38]和Brier评分(Brier Score,BS)[39]作为评价准则对模型的性能进行评估。CI值主要衡量模型的区分度,BS主要衡量模型的正确率。CI值的计算式如公式(1)所示。其中,n为样本数量,K为预测结果与实际结果一致的配对样本数量,M为预测结果与实际结果一致的配对样本数量。CI值的取值范围为[0.5,1],且CI值越趋近于1,则证明预测效果越好,若CI值结果小于0.6,则证明模型预测结果较差。
(1)

(2)
3.2.3 基于SHAP的解释器模型构建
本文采用SHAP方法[40]构建可解释模型。与一般的机器学习可解释性方法不同,SHAP不仅可以解释不同因素的特征重要性,还可以解释不同因素的边际贡献,同时也能够提供对单个样本的局部解释,在解释过程中不会受因素间多重共线性的影响[41],因此SHAP方法可以用于量化揭示不同因素对专利维持时间的影响。Shapley值的计算方法如公式(3)所示。
(3)

4 实证分析
4.1 数据准备与实验设置
4.1.1 数据获取与处理
由于世界各国对发明专利的保护期限及年费缴纳制度有不同的规定,各国的经济环境和政策环境也不尽相同,故为避免由此带来的误差,本文仅选择在中国国家知识产权局进行申请并获得授权的发明专利集作为初始专利数据库。我国的专利制度于1985年实施,至今历经多次改革,为避免不同时期专利维持情况的差异,本文将样本的时间窗口设置为2001—2017年。根据上述策略,本文采用incoPat数据库进行数据采集,根据incoPat数据库的检索规则,制定如下检索式:(AD=[20010101 to 20171231]) AND (PNC=(CN)) AND (PAT=4)。
根据上述检索式共收集到3,851,819件专利文献数据,根据所构建影响因素指标体系中技术循环周期、技术原创性和技术激进性的指标测度的要求,为避免上述指标出现大量空值带来噪声,采用德温特世界专利索引(Derwent World Patents Index,DWPI)以及INNOGRAPHY数据库补充检索专利的引文数据,将后向引证频次和前向引证频次为0的专利去除。最终共得到510,614条专利数据,包含350余万条引用和被引用信息,数据的时间分布如图2所示。在样本数据确定后,根据31项影响因素对应的测度方式,提取相应的特征变量构建特征数据集。特征数据集构建完成后,统计各因素项的缺失值,然后通过随机森林算法对缺失值进行插补,完成后随机将数据集按照7∶3的比例划分为训练集和测试集。

图2 数据样本时间分布图
4.1.2 基准模型设置与评估
为防止XGBoost模型出现过拟合问题,同时保证模型具有较高的预测精度,本文采用贝叶斯优化算法对影响模型性能的主要参数进行超参数调节,调参过程中使用负对数似然函数作为损失函数并以此作为调参过程中的评价标准。根据上述调参方法,得到模型主要参数的最优值:learning_rate=0.110,max_depth=7,lambda=0.796,alpha=0.002。根据最优参数迭代10000次训练模型,并采用10折交叉验证的方式得到模型在测试集上的平均CI值为0.789,平均BS值为0.131,表明模型具有较高的准确性,可以采用该模型作为算法归因框架的基准模型。在得到最优基准预测模型后,采用Python语言调用SHAP工程包构建解释器。
4.2 全样本因素效应探索性分析
4.2.1 全样本因素重要性分析
本文根据公式(3)对每个样本都进行一次因素的Shapley值计算,在得到每个样本各因素的Shapley值后,将所有样本在同一因素上的Shapley值进行加和后求平均,得到不同因素对专利在观察期内生存风险的影响程度。由于SHAP方法满足可加性原理,所以先天因素、行为因素和环境因素的总Shapley值可由各具体因素的Shapley值加和得出,各因素的全局重要性解释如图3所示。
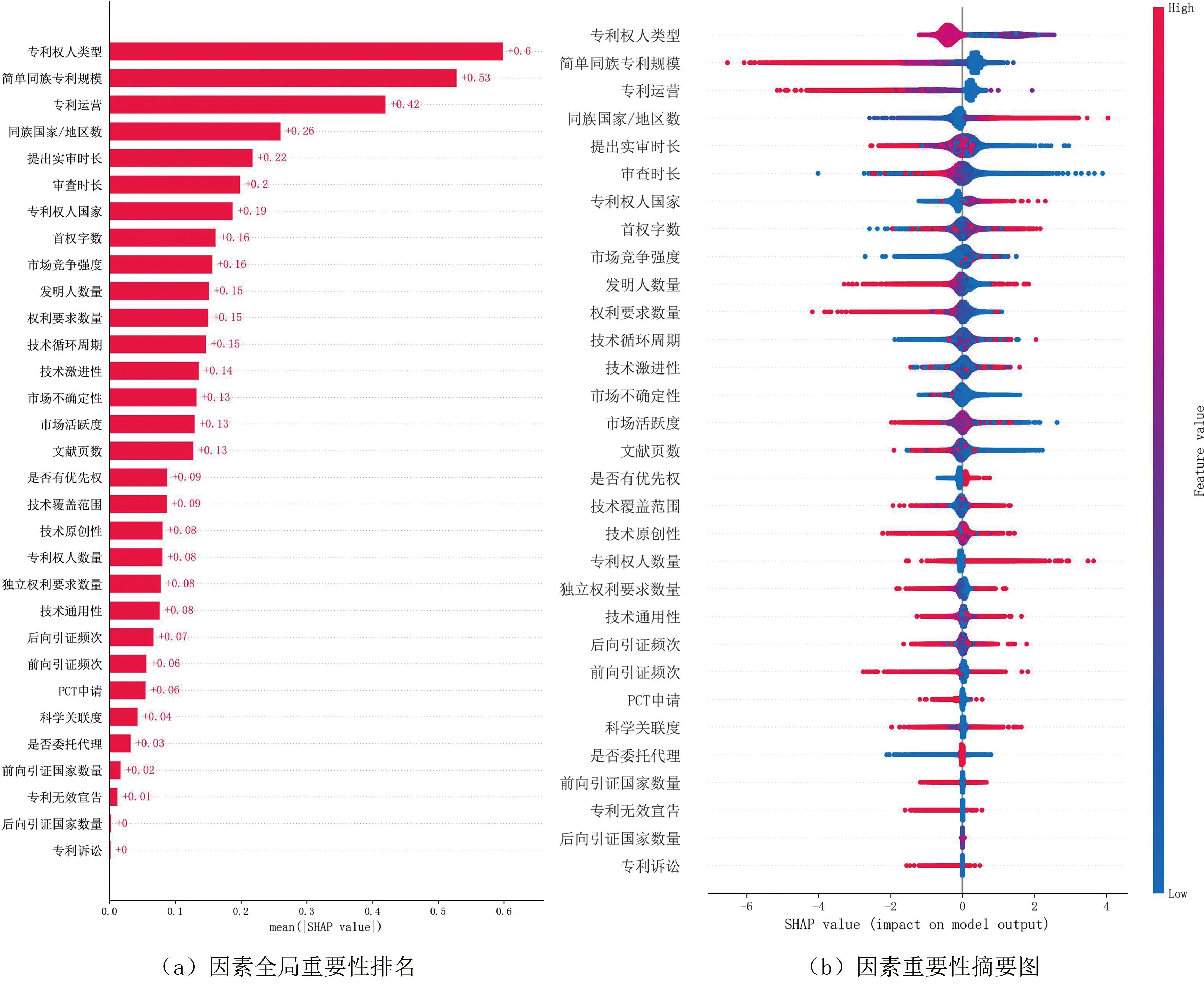
图3 各影响因素的全局重要性图
由图3可知,先天因素、行为因素和环境因素的重要性分别为1.91、1.42和0.62,说明先天因素对专利是否继续维持的影响最大,与上文的理论分析一致。图3(b)不仅展示了各因素的Shapley值,还反映了不同因素对专利维持时间的作用方向,其中红色代表因素在样本点上取值较高,蓝色代表因素在样本点上取值较低,每个因素的影响效应图由数据集内的所有样本点构成。由于Cox-XGBoost模型最终的输出是专利的生存风险概率,故在坐标轴左侧的样本点对专利的维持具有正向影响,在坐标轴右侧的样本点对专利维持具有负向影响。专利权人类型、简单同族专利规模、专利运营、提出实审时长、审查时长、发明人数量和权利要求数量等因素的取值越高,其Shapley值越低,说明这些因素是专利维持的保护因素,而同族国家/地区、专利权人数量和首权字数等因素的取值越高,样本点的Shapley值越高,说明这些因素是专利维持的危险因素。
为对比基于机器学习模型的算法归因和传统统计学归因方法在归因解释方面的异同,本文采用Cox模型对专利维持时间的影响因素进行了分析,分析结果如表2所示。由表可知,不同因素的Shapley值排名与Cox模型回归系数的大小和显著性情况基本一致,专利权人类型、简单同族专利规模和专利运营等对专利维持时间有显著影响的因素基本也位于Shapley值排名的前列,这说明算法归因框架可以有效获取变量间的影响效应关系。与Cox模型统计归因方法相比,基于算法的归因框架不仅可以对全局进行解释,也可以对不同因素对微观个体的影响进行解释,故基于算法归因的方法探究专利维持时间的影响因素具有一定优越性。

表2 Cox模型分析结果
此外,根据前人研究,同族国家/地区数与专利价值之间存在正相关关系,即同族国家/地区数越多专利价值越高,而专利价值和专利维持时间之间也为正相关关系[38-39],故同族国家/地区数与专利维持时间之间也应该是正相关关系,而本文却得出了与之矛盾的结果。针对这一现象可能的解释是,传统归因方法得出的结论有一定的局限性,仅考虑到同族国家/地区数与专利维持时间或专利价值之间的线性关系,未考虑到同族国家/地区数与其他因素之间的交互效应或者其他因素对其的调节效应。而本文算法归因框架是基于数据和模型驱动的,目的是挖掘不同数据之间的关联模式,更多考虑的是不同数据之间的非线性关系,故对于同族国家/地区数这一因素而言,两种方法得出相反的结论属于正常现象,未来需要进一步探究不同因素之间的交互效应,才能得出更加可靠的结论。
4.2.2 不同文献生命周期阶段因素重要性分析
由于在不同时间申请的专利,其所处的生命周期阶段有所不同,例如2001年申请并获得授权的文献已经处在生命周期的末期,而2017年申请的专利则处于生命周期的早期。本文根据专利申请时间分布将专利文献划分为17个时间区间,并按照成长期、成熟期和衰退期将专利文献划分为三个生命周期阶段(如图4所示),按照时间区间分别计算各子因素的Shapley值,并通过公式(4)计算各子因素的Shapley值的当年占比[40],其中I为各因素的集合,i为各个子因素项,φi为各子因素当年的Shapley值,ωi为各因素Shapley值的当年占比。
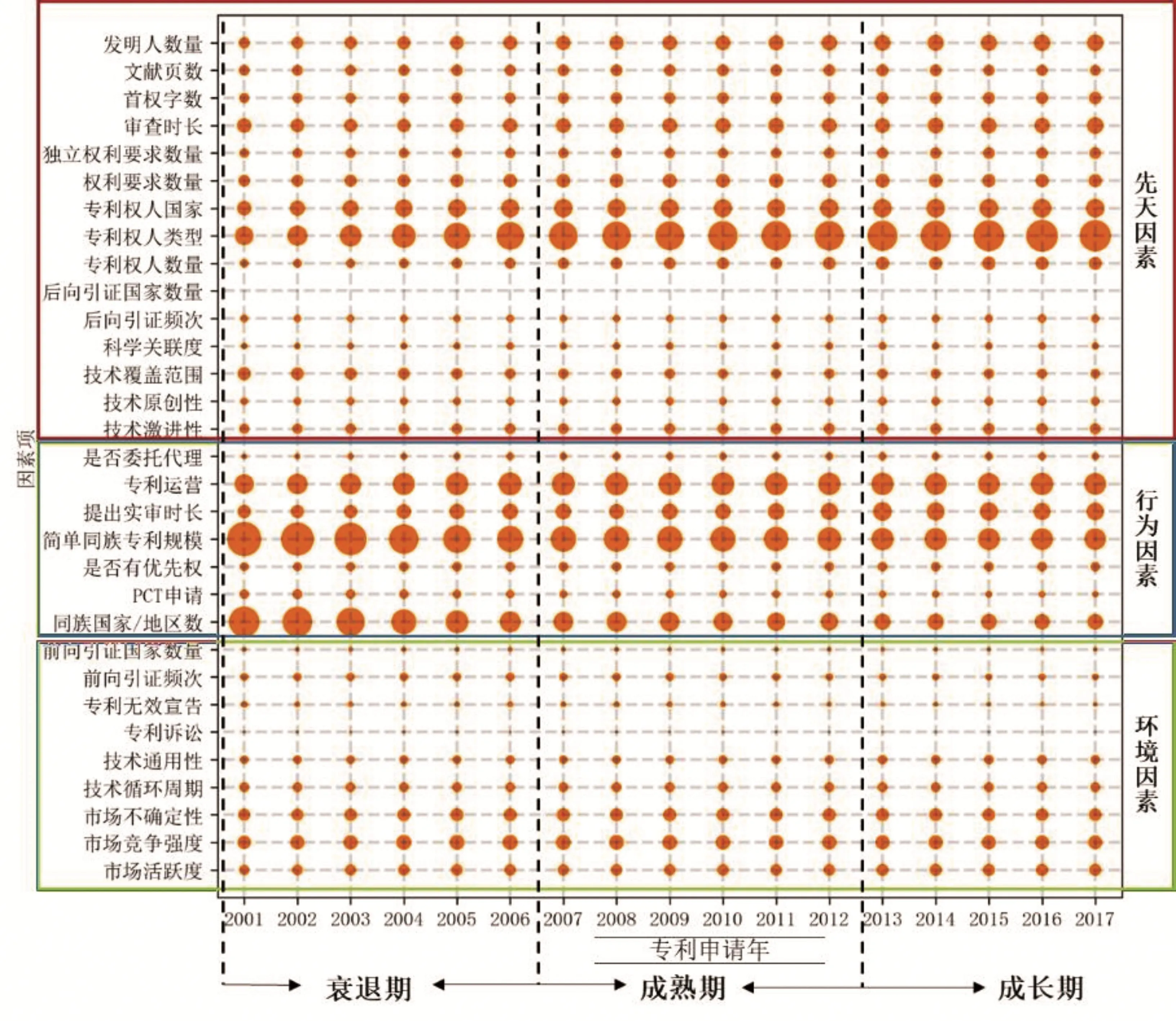
图4 各子因素的绝对平均Shapley值占比随生命周期的变化图
(4)
图4显示了各子因素的重要性占比变化趋势,图中气泡大小表示ωi值,由图可知,大部分子因素的重要性占比并未出现较强的生命周期变化趋势,这也证明了各因素对专利维持时间的影响效应较为稳定。在先天因素中,专利权人类型的Shapley值占比呈现明显的生命周期变化趋势,在专利文献的生命周期早期(成长期),专利权人类型对专利维持时间的影响程度较大,而在成熟期和衰退期,专利权人类型对专利维持时间的影响程度逐渐降低。可能的原因是:在专利文献的生命周期早期,不同专利权人申请专利的目的和动机各不相同,对于大部分高校和科研院所而言,其专利申请是由评奖评优、职称评定驱动的,申请专利的动机并不是为了保护自身的技术,虽然其申请的专利所保护的技术具有较高的创新性,但在专利申请获得授权后,部分专利权人便不会继续缴纳年费以维持专利权有效性;对于企业而言,其申请专利的目的是保护自身的技术方案和产品,从而在法定保护期占据一定的垄断地位,获得更多的收益,因此企业在专利申请获得授权后的前期更加倾向于维持专利权有效。而在专利文献的成熟期和衰退期,随着技术和产品的不断更新迭代,专利所保护技术方案的技术价值和经济价值逐渐衰退,原有技术和产品可能已不再适应市场需求,此时专利是否维持更多地取决于其法律价值,故在此时专利权人的类型对于专利维持时间的影响程度逐渐减弱。
在行为因素中,同族国家/地区数和简单同族专利规模对专利维持的影响呈现明显的生命周期变化趋势。在专利文献生命周期的早期,同族国家/地区数和简单同族专利规模对专利维持时间的影响程度较小,在成熟期和衰退期,上述两个因素项对专利维持时间的影响程度较大。究其原因,在专利生命周期的早期即成长期,大部分专利申请人仅仅关注国内市场,并未开展专利的国际布局,因此大部分专利的同族国家/地区数以及简单同族专利规模相似,上述两个因素对专利维持时间的影响程度较小;在专利生命周期的成熟期和衰退期,大部分专利会因其技术价值和经济价值逐渐贬值而失效,而对于布局国家数量和同族专利数量较多的专利而言,由于其对于专利权人具有较高的法律保护价值,即使专利的技术价值和经济价值较低,专利权人也会因其具有较高的法律价值而倾向于继续维持该专利,直至专利因期限届满而失效。由此也可以说明对于衰退期的专利而言,其是否具有独特的法律价值对于其维持时间具有较大的影响。
在环境因素中,各因素项对专利维持时间的影响与其他因素项相比则较小,也未见有明显的变化趋势,这说明市场环境对不同生命周期的专利而言,其影响程度较为稳定,不会随专利文献生命周期的变化而变化。究其原因,专利申请对于专利权人而言是在法定保护期内使专利权人占据一定的垄断地位,使其能够在激烈的市场竞争中占据一定优势,对于不同生命周期阶段的专利而言,其是否维持都会受到市场环境因素的间接影响,所以市场环境因素对专利维持的影响较为稳定。
为进一步探究先天因素、行为因素和环境因素随专利文献生命周期的变化趋势,本文绘制了如图5所示的三大因素重要性的生命周期变化趋势图。由图可知,在专利生命周期的早期即成长期阶段,先天因素对专利维持时间的影响最大,其次是行为因素,最后是环境因素;在专利生命周期的成熟期阶段,先天因素对专利维持时间的影响程度略高于行为因素,环境因素对专利维持时间的影响程度最小;在专利生命周期的衰退期,行为因素对专利维持时间的影响程度最大,其次是先天因素,最后是环境因素。在不同的生命周期阶段,环境因素对专利维持时间的影响程度大致相同,而行为因素和先天因素对专利维持时间的影响程度变化较大,这与上文分析结果基本一致。
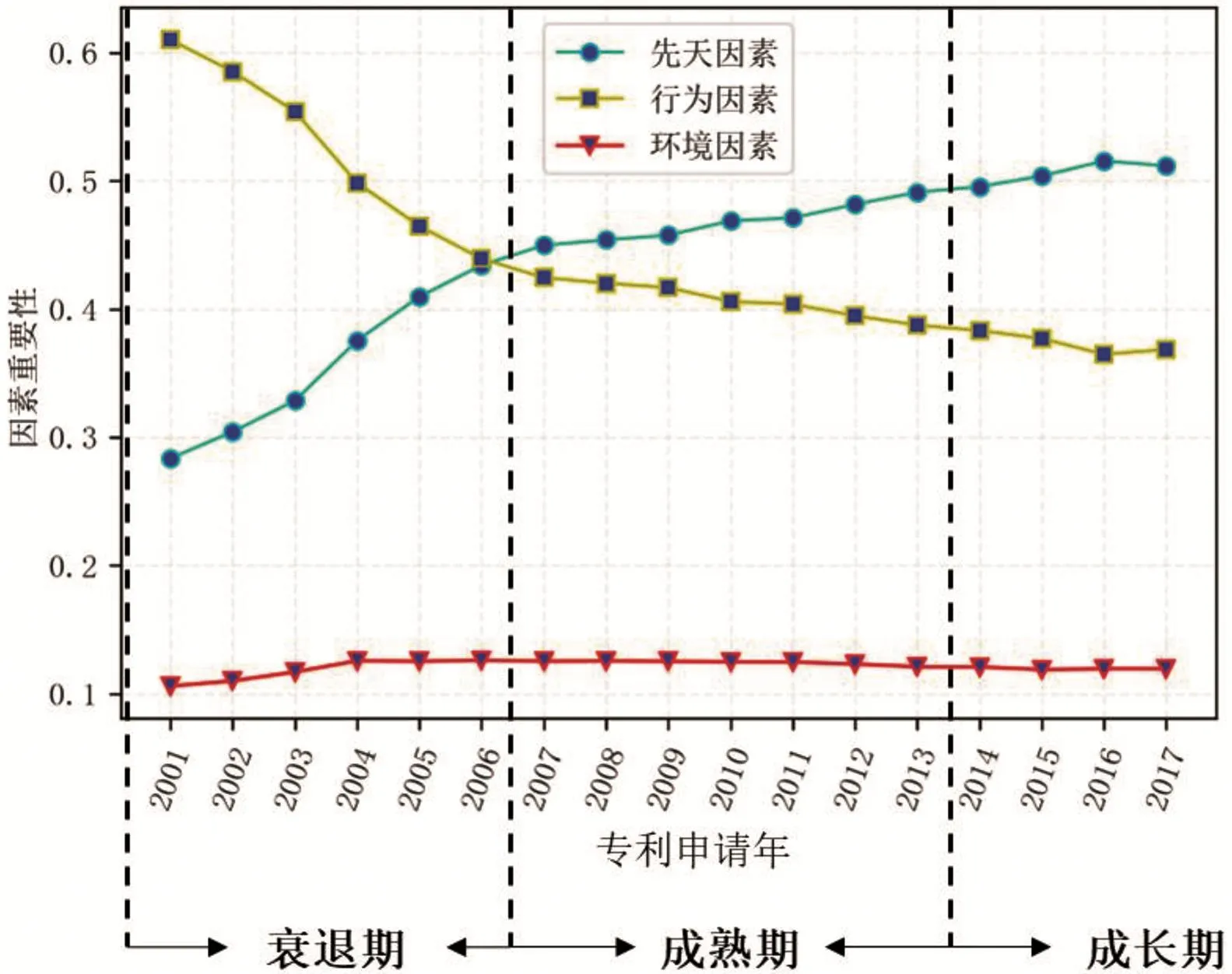
图5 三大因素重要性生命周期变化图
4.2.3 不同领域的因素重要性分析
为进一步分析在不同技术领域内各影响因素项对专利维持时间的影响效应,本文按照IPC代码的部,将专利分为A部(人类生活必需品)、B部(作业;运输)、C部(化学;冶金)、D部(纺织;造纸)、E部(固定建筑物)、F部(机械工程;照明;加热;武器;爆破)、G部(物理)、H部(电学)8个不同的技术领域,根据公式(4)计算各子因素在不同技术领域内的Shapley值占比,按照计算结果绘制了如图6所示的热力矩阵图,图中颜色越深表明因素重要性越高。由图可知,不同因素在不同技术领域的重要性排名与全局解释时的排名一致,专利权人类型、专利运营、同族国家/地区数和简单同族专利规模在不同技术领域内的重要性依旧排名前列。不同技术领域之间相同因素的重要性略有差异,例如,专利权人类型在E部的重要性明显高于其他领域,而同族国家/地区数和简单同族专利规模的重要性要弱于其他技术领域,市场活跃度和市场竞争强度在A部的重要性要略高于其他技术领域。这可能是由于不同技术领域,技术成熟度、技术创新难度和专利申请文件撰写的方式具有一定差异,在技术成熟度较高、技术创新难度较低的技术领域,只有占据行业领先地位和核心地位的企业才会投入较高的费用进行新技术的研发和专利的申请与维持,从而形成行业的垄断地位,所以针对此类技术领域的专利而言,先天因素中的专利权人类型、专利权人国家和发明人数量对专利维持的影响较大。在医药、化学和电学等领域,技术创新难度较大、技术更新速度较快、市场竞争强度更高,所以市场活跃度、市场竞争强度和市场不确定性对专利维持的影响要大于其他技术领域。

图6 不同技术领域各子因素Shapley值占比图
图7显示了先天因素、行为因素和环境因素在不同技术领域内的重要性占比,由图可知,三大因素在不同技术领域的重要性排名与全局解释时排名基本一致。先天因素在E部和G部的重要性略高于其他技术领域,而行为因素和环境因素略低于其他技术领域,环境因素在A部、D部和F部的重要性略高于其他技术领域。这类差异的可能原因在于,不同技术领域之间存在固有的内生性差异,在建筑、机械工程和纺织技术(B部、D部、E部、F部)等较为成熟的技术领域,专利的产出较少(占全部专利的26.28%),技术领域内的市场竞争强度和专利交易的活跃度较低,故在上述领域专利的先天因素与其他领域相比占比更高。而在医药、生物技术、化学冶金和电学领域(A部、C部、G部、H部),市场需求旺盛、创新主体数量庞大、每年的专利产出数量较高(占全部专利的73.72%),但是上述领域技术创新难度较大,虽然专利产出较多,但是真正能够产业化并被市场认可的专利技术较少,加之激烈的市场竞争促使上述领域的相关创新主体不断进行技术更新迭代,从而导致专利的维持时间逐渐缩短,因此行为因素和环境因素对专利维持的影响更大。
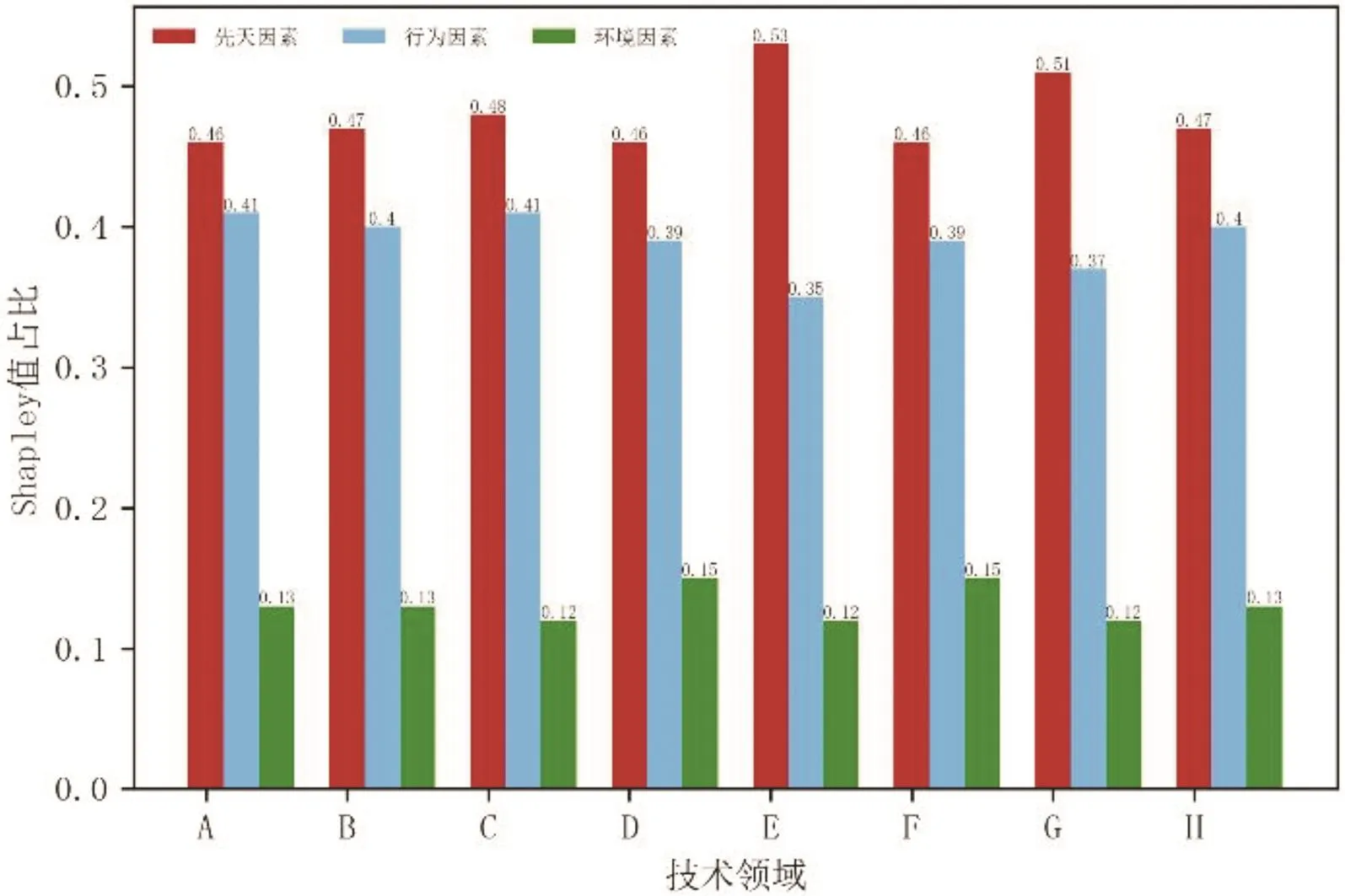
图7 三大因素在不同技术领域内的重要性对比
4.2.4 因素效应关系分析
通过全局重要性能够大致判断不同因素对专利维持时间的影响,但是无法对因素与专利维持之间的非线性关系进行更为细微的观测。因此,本部分根据各因素的Shapley值绘制了各因素与专利维持时间之间的SHAP依赖图,如图8所示(由于篇幅原因,本部分仅展示各因素中重要性排名靠前的子因素的SHAP依赖图),图中一个点表示一个专利样本,横坐标为样本因素的取值,纵坐标表示样本该因素的Shapley值,若样本点的Shapley值大于0,表明该因素取值提升了专利生存风险,若样本点的Shapley值小于0,表明该因素取值降低了专利生存风险。

图8 各子因素的影响效应关系图(部分)
当专利权人类型为科研单位、企业或者共同申请时,专利的生存风险率较低,说明科研院所和企业的专利申请维持时间会更长。在专利权人国家当中,当申请人为中国申请人时,Shapley值均小于0,而申请人国别为美国、日本和韩国等其他国家时,大部分样本点的Shapley值大于0,这说明相较于国外申请人,国内申请人的专利失效风险率更低。当发明人数量大于4时,大部分样本点的Shapley值小于0,这表明发明人数量一旦超过4,专利维持时间会更长。权利要求数量的Shapley值呈现明显的下降趋势,当权利要求数量超过10时,大部分样本点的Shapley值会低于0;当权利要求数量超过100时,样本点的Shapley值均小于0,可能原因在于权利要求数量表示专利的保护范围和权利稳定性,当专利的权利要求数量越多时,专利的保护范围越大,权利基础也更加稳定,法律保护价值越高。技术激进性呈现出W型的波动效应,这说明技术过于激进对专利的维持具有负向效应。
专利运营因素的SHAP依赖图表明,专利交易的次数越多,专利维持时间会更长,原因是交易次数越多的专利,商业价值会更高,专利维持时间越长带来的收益越高。大部分样本的扩展同族专利规模都集中在0至100之间,当扩展同族专利规模的值大于10时Shapley值都小于0,说明扩展同族专利规模超过10项以后,专利的失效风险会更低。专利家族规模对专利维持的影响呈现先小幅下降,后大幅上升后又小幅下降的趋势,但是大部分样本点的Shapley值均高于0,说明专利家族规模越大,越不利于专利的维持,可能的原因是,当专利家族规模越大时,所需投入的专利维持成本会越高,一旦专利的价值不足以弥补专利维持费用后,专利权人便会放弃维持。大部分样本点的提出实审时长的Shapley值小于0,说明提出实审时长越长,专利维持时间越长,这可能与本文对专利维持时间的定义有关,即实审时长和维持时间是部分与整体的关系,故其对专利维持具有正向效应。
审查时长与专利维持时间也是部分与整体的关系,故审查时长越长,专利维持时间也会越长。当样本点的市场竞争强度值升高时,Shapley值也会相应升高,当市场竞争强度值高于500时,Shapley值均高于0,说明市场竞争强度越高,技术淘汰速度越快,专利维持时间会越短。市场活跃度的SHAP依赖图呈现明显的U型曲线,当市场活跃度小于0时,Shapley值逐渐降低,市场活跃度大于0时,Shapley值逐渐升高,这说明当技术市场区域稳定和成熟时,专利的维持时间会更长,当技术市场处于发展期时,市场的“洗牌”速度会更快,从而导致专利维持时间变短。
根据上述分析,本文总结了如图9所示的不同因素对专利维持的影响框架。首先,影响专利维持的三种因素之间会相互影响,其中先天因素和环境因素均会影响专利权人的行为因素,三种因素形成的联动效应会直接影响专利的维持时间。例如,不同类型的专利权人,由于专利申请的动机不同,专利运营和专利布局等行为也会不同;同时,在不同的市场环境下,专利权人也会有不同的专利运营策略和保护策略。此外,在不同的文献生命周期阶段以及不同的技术领域,不同因素对专利维持时间的影响效应略有差异,因此,文献生命周期阶段和专利所处的技术领域会对上述因素的影响效应产生调节作用。

图9 不同因素对专利维持的影响框架
4.3 稳健性检验
4.3.1 多模型训练与精度评估
在算法归因框架中,本文以Cox-XGBoost模型作为基准模型,然而,基于生存分析方法的机器学习模型还包括生存树(Survival Tree,ST)、随机生存森林(RandomSurvival Forest,RSF)、极端随机生存森林(Extremely Random Survival Forest,ERSF)和深度神经网络生存分析(DeepSurv),前三种是基于树模型的生存分析机器学习模型,DeepSurv是基于深度神经网络的生存分析机器学习算法。本文进一步建立了上述四种模型,采用相同数据集对模型进行训练和评估,最终得到模型的性能如表3所示。通过不同模型的效果比较来看,机器学习模型的CI值均在0.7以上,其中XGBoost模型的CI值最高,为0.789,远高于Cox模型的0.695;BS值均在0.15以下,均小于Cox模型的0.151。综上,基于机器学习模型的生存分析方法性能高于传统的Cox模型,确保了基于机器学习的算法归因框架结果的准确性和稳健性。

表3 多类机器学习模型的效果比较
4.3.2 基于排列特征重要性的因素重要性检验
为保证本文算法归因框架挖掘出的因素与专利维持之间的关系不受模型和归因方法的影响,本研究进一步采用Cox-XGBoost模型的信息增益方法和RSF算法的排列特征重要性算法对专利维持时间影响因素的重要性进行挖掘,并将结果与上文实证结果对比,以验证结果的稳健性,检验结果如表4所示。基于Cox-XGBoost模型信息增益算法得到的因素重要性排名与基于Shapley值的因素重要性排名虽然略有差异,但是差异并不明显。另外,基于RSF模型得到的排列特征重要性不仅可以反映因素的重要性,也反映了因素对专利维持时间的影响方向,基于RSF模型得到因素的排列特征重要性及其影响方向与上文得到的因素重要性和影响方向虽然具有略微差异,但是大部分因素的影响方向和重要性与上文分析结果一致。 综上, 基于算法归因框架得到的影响因素重要性及其对专利维持时间的影响方向较为稳定。

表4 基于RSF的排列重要性算法的因素重要性结果
5 研究发现与结果讨论
5.1 研究发现
本文从生物学理论角度出发,采用Cox-XGBoost模型和可解释性机器学习方法构建了算法归因框架,并根据该框架对中国2001—2017年的专利数据进行了实证分析,挖掘专利维持时间的主要因素,并对不同因素的影响效应进行了揭示。
研究表明,本文构建的算法归因框架与传统归因方法相比,不仅可以挖掘高维非线性因素对专利维持时间的影响效应,在分析不同因素对微观样本的具体影响效应方面也具有一定的优越性。此外,研究表明先天因素对专利维持时间的影响最大,其次是行为因素和环境因素,这与Choi等[29]的研究有一定出入,他们认为环境因素对美国专利维持的影响更大,本文对该差异的解释是:在Choi等的研究中,没有将市场竞争、市场的活跃性和市场不确定性等市场因素加入,仅仅是采用部分文献计量指标进行测度;此外,其衡量因素重要性的方式为Wald统计量,但是在传统的统计归因模型中,因素重要性采用Wald统计量的卡方值进行检验更为准确;最后,在不同经济环境和政策环境下,专利的维持是具有差异的,本文是以中国专利作为样本进行分析,而Choi等是以美国专利作为样本,故出现上述差异是正常的样本选择性偏差。除上述差异外,本文对所选影响因素的影响效应分析结果与现有研究[10-16]的分析结果基本一致。此外,本文还对前人未曾研究的市场竞争强度、市场活跃度、市场不确定性、技术原创性、技术激进性和技术通用性等因素进行了测度和分析,同时还对不同因素在不同专利文献生命周期阶段、不同领域以及不同因素的效应关系进行了详细探究,这些指标可以为未来探究不同市场环境下专利维持行为提供一定的借鉴和参考。
5.2 结果讨论
在数智时代,机器学习模型的应用领域不断扩展,在专利维持时间预测领域,也应该积极引进智能算法,通过多源数据融合的方式,构建专利维持预测模型,进而帮助企业构建完善的专利预警体系和完善的竞争情报系统,提升企业在专利竞争中的竞争力。本文的主要贡献在于:一是构建了基于可解释机器学习的算法归因框架,可以揭开机器学习这一“黑盒模型”的神秘面纱,以数据和模型驱动的方式揭示不同因素对专利维持的真实影响效应,可为专利维持时间的相关研究提供新方法,同时也可为未来专利维持时间的预测提供理论支撑,避免过度依赖数据和算法的负面效应;二是从生物学视角构建了专利维持时间的影响因素指标体系,并在现有指标的基础上进行了扩展,同时采用大规模专利数据集对指标的影响效力进行了验证,这为未来专利维持时间影响因素、专利价值评估以及专利年费制度等相关研究提供了新的理论视角及研究指标。
当然,本研究还存在以下不足:一是在样本选取方面,囿于数据的处理能力,仅选择了中国专利作为样本进行了纵向的分析,并未收集其他国家专利进行横向扩展的研究;二是在影响因素方面,仅基于专利结构化数据对影响因素进行了测度,并未结合专利文本语义数据、经济数据和行业发展数据。三是在研究方法和研究模型方面,本文仅采用了现有的生存分析机器学习模型,并未对模型进行改进,使其更加适用于专利维持时间预测及相关研究。在未来,可以考虑收集不同国家的专利维持数据,从多个角度探究不同国家专利维持特征的差异,深入分析专利文献计量指标与专利维持之间的相关性及其因果关系;此外,在多源数据环境下,可以考虑将经济数据、行业发展数据、企业运营数据与专利数据进行融合,基于融合数据集,对生存分析机器学习模型进行进一步改进,使其更加适用于专利维持数据,进而构建可靠、准确、科学的专利维持时间预测模型;最后,可以进一步拓宽专利维持时间预测模型的应用场景,例如可以将专利维持时间预测模型进一步应用于核心专利识别和潜在高价值专利识别当中。
