不同侧隙卸荷槽时齿轮泵理论流量的创新计算
2024-02-28李玉龙宋安然
刘 萍,李玉龙,宋安然
(宿迁学院 机电工程学院,江苏宿迁 223800)
0 引言
外啮合齿轮泵(简称为齿轮泵)为依靠2 个同尺寸齿轮在1 个紧密配合的壳体内相互啮合旋转,从而实现介质输送或增压的一类容积式动力元件[1-5]。虽结构简单,应用广泛,但齿轮副啮合半径的周期性变化和重合度大于1,造成了流量脉动[6-7]和困油现象[8]等严重的结构性问题。侧隙的有和无[9-10]、双卸荷槽设置对称与否[11-12]的不同类型,简称为多类型,对输出流量和困油现象均有较大的影响,其中,影响程度分别用类型系数[13]和最大困油容积变化率[14]加以评估。目前,输出流量公式多为单一类型下基于文献[13]而推导的,其中,来自困油腔通过卸荷槽的卸荷流量,对出口腔内输出流量的损益影响最为关键[15-17],输出流量计算的周期性啮合线区间多为齿顶啮合后的有侧隙1 个、无侧隙半个的基圆节距[18]。显然,这些单一类型及卸荷流量损益影响下的输出流量研究,局限性大,过程分析复杂,难免会出现一些错误性结论[19]。鉴于此,拟通过一种不直接考虑卸荷流量影响的新计算方法,以期实现多结构类型下理论输出流量及理论排量和理论脉动系数等衍生量的快速求解及其统一式的精确构建。
1 现有类型系数中的问题
文献[13]中通过进口腔或出口腔封闭体积的扫过面积方法,给出了齿轮泵理论排量:
式中,B 为齿宽;Re为齿顶圆半径;R 为节圆半径;Pb为基圆节距;Kc为类型系数,多类型下现有的类型系数见表1[13]。

表1 现有的类型系数Tab.1 Existing type coefficients
1 对互相啮合的齿轮,在其非工作面间沿公法线方向(即沿啮合线方向)上的间隙简称为侧隙,泵用同尺寸齿轮副的侧隙值cn,一般取为0.01mn~0.08mn[13],且:
式中,mn为模数,mm;μ为介质黏度,N·s/m2;v 为节圆圆周速度,m/s;Δp 为高低压腔压力差,MPa。此时,视为无侧隙或小侧隙,否则视为有侧隙或大侧隙[13]。
在表1 中,由“无侧隙”下“无卸荷槽”、“低压单侧卸荷槽”和“高压单侧卸荷槽”的现有类型系数均为Kc=3ε2-3ε+1,ε为重合度,可类比推理出“有侧隙”下该3 种卸荷槽的类型系数应相同。同样,由“无侧隙”下“低压单侧卸荷槽”和“高压单侧卸荷槽”的现有类型系数均为Kc=3ε2-3ε+1,可类比推理出“有侧隙”下该两种卸荷槽的类型系数也应相同,由此可见现有的部分类型系数是错误的。其中,单侧卸荷槽为双卸荷槽省略了另一侧卸荷槽的特殊情况,这里统称为双卸荷槽。
2 泵用齿轮副的周期性啮合过程
由2 个同尺寸齿轮所构成齿轮副的啮合过程如图1 所示。其中,O1,O2分别为主、从动渐开线直齿轮的中心,p 为节点,m 为单齿或双齿中后进入啮合的轮廓点,n 为双齿中先进入啮合的轮廓点;F 为节点p 到点m 间啮合线段的矢量长度,f=F/Pb为对应于F 的无量纲矢量长度,以与主动轮旋转方向相同时为正,否则为负;以“□”符号表示侧隙位置;ω为旋转角速度,Rb为基圆半径,点m 与点n 间的啮合线长度等于基圆节距Pb。
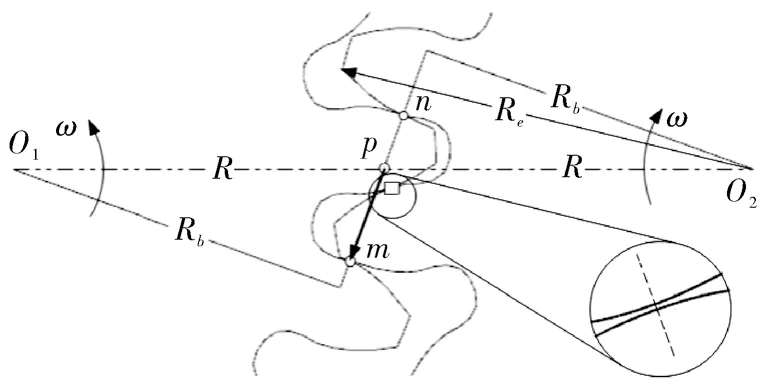
图1 齿轮副周期性的啮合过程Fig.1 The periodic meshing process of gear-pair
以f 作为齿轮副啮合的无量纲位置变量,则在1 个齿轮的完整齿面上,点m 由Re到Rb的周期性啮合所对应的啮合线长度等于εPb,称之为齿面啮合线区间,对应的啮合流量称为齿面流量Q0。由于1 个无侧隙位置可视为1 个啮合点,所以齿轮副周期性啮合输出所对应的啮合线长度等于kPb,称之为输出啮合线区间,对应的啮合流量称为输出流量Q,其中,k=1 表示有侧隙类型,k=0.5 表示无侧隙类型。
3 无卸荷槽时的齿面流量和输出流量
案例计算时齿轮副参数统一采用压力角为20°,齿顶高系数为1.0,齿数为14,模数为3,变位系数为0,齿宽B=30 mm;由此计算得出ε=1.46,R=21 mm,Re=24 mm,Pb=8.86 mm。工况参数采用转速1 500 r/min,即ω=157.08 rad/s。
由文献[13],得齿面流量Q0为:
式中,re=Re/Pb为无量纲齿顶圆半径;r=R/Pb为无量纲节圆半径。
有侧隙无卸荷槽时,在输出啮合线区间Pb内,会出现双齿、单齿啮合的2 个子区间,案例参数下的齿面流量Q0(f)和输出流量Q(f),如图2 所示。其中,双齿啮合区间即为有侧隙困油的啮合线区间,如图2 中剖面线部分。据此,得出矩形框内的输出流量Q 为1 个以Pb为区间的周期函数,则Q的均值与Pb子区间的起点s 在εPb区间内的选择无关。

图2 有侧隙和无卸荷槽时的输出流量Fig.2 Output flow with backlash and without oil-trapping relief groove
无侧隙无卸荷槽时,在Q 的形成过程中,无侧隙位置相当于1 个啮合点,因此在1 个输出啮合线区间0.5Pb内,存在着前侧隙位置+啮合点+后侧隙位置的三齿、侧隙位置+啮合点的双齿啮合的2 个子区间,相应的齿面流量Q0(f)和输出流量Q(f),如图3 所示。

图3 无侧隙和无卸荷槽时的输出流量Fig.3 Output flow with backlash and without oil-trapping relief groove
其中,三齿、双齿啮合线区间将分别形成2 个和1 个无侧隙的困油区间,如图3 中双齿啮合下打剖面线的部分为无侧隙困油区间。据此,得矩形框内的Q 为1 个以0.5Pb为区间的周期函数,则Q 的均值与0.5Pb子区间的起点s 在εPb区间内的选择无关。
4 双卸荷槽下的输出流量特性
依据双卸荷槽的设置原则[20],双卸荷槽间距内的啮合线段se,称为卸荷槽啮合线间距,与无卸荷槽输出流量Q 的啮合线区间kPb相同,如图4 所示。其中,点s,e 分别为点m,n 一侧卸荷槽的槽口线与啮合线的交点,a1,a2分别为主从动齿轮的齿顶点。

图4 双卸荷槽下的齿轮副啮合过程Fig.4 The meshing process of gear-pair with double oil-trapping relief groove
线-εPb,(2k-ε)Pb表示m 点为齿顶啮合位置及其相应的n 点位置,线-(2k-ε)Pb,εPb表示n点为齿顶啮合位置及此时m 点的位置,线-0.5kPb,0.5kPb表示m 点、n 点关于节点p 对称时的啮合位置。Y 为双卸荷槽的对称线相对于齿轮副的中心线O1O2的不对称啮合线宽度,y=Y/Pb为对应于Y的无量纲不对称啮合线宽度,y 可用于定义双卸荷槽设置的不同类型,其正负和前述f 的正负定义一致。其中,由双卸荷槽的设置原则[13],得y 的取值范围为:
基于前述无卸荷槽输出流量Q 及其均值与kPb子区间起点s 的选择无关,则如以卸荷槽啮合线间距se 作为输出流量Q 的计算区间,就可不直接考虑卸荷流量对输出流量Q 计算的影响。例如,在如图4 所示的逆时针旋转方向下,啮合点m 始终远离槽口线-0.5kPb,困油腔与出口腔将始终没有卸荷流量的交换。
此时,输出流量Q 即为卸荷槽啮合线间距kPb内的齿面流量Q0,如图5 所示。其中,s 点处f=y-0.5k,点e 处f=y+0.5k,Max 点处为最大瞬时流量位置(f=0)。
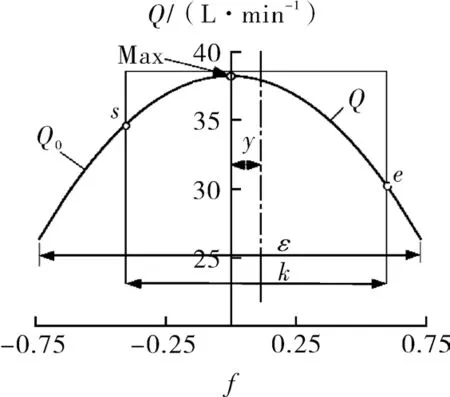
图5 从齿面流量曲线中提取输出流量曲线Fig.5 Extract output flow curve from full tooth surface flow curve
由一般要求ε<1.5[10],得有侧隙(k=1.0)下点(f=0)位于双卸荷槽间的啮合线长度se 内;无侧隙(k=0.5)下且-0.25 ≤y ≤0.25 时,点(f=0)位于se内,否则位于se 外。
5 多类型下输出量的统一简洁式
由图4 中a1O1mO2a2封闭区域的扫过面积方法,得出多类型下输出流量Q 为:
则,输出排量q 为:
说明对称卸荷槽类型(y=0)或无侧隙类型(k=0.5)下的排量最大。
由流量脉动系数的定义:
式中,max(Q),min(Q),ave(Q)分别为输出流量Q 的最大值、最小值和均值。
有侧隙(k=1.0)时,图5 中最大瞬时流量位置点(f=0)位于se 上,所以Q 满足:
可得出有侧隙(k=1.0)的流量脉动系数β为:
无侧隙(k=0.5)时,图5 中最大瞬时流量位置点(f=0)既可能位于se 内也可能位于se 外,所以,此时Q 满足:
可得出无侧隙(k=0.5)的流量脉动系数β为:
由y=0,k=1.0,0.5,可得:
与文献[13]给出的流量脉动式完全一致,由此说明式(5)~(11)的正确性。
在案例参数下,由式(9)(12)得到的流量脉动系数,如图6 所示。由此说明对称卸荷槽类型(y=0)或无侧隙类型(k=0.5)下的流量脉动更小,单侧卸荷槽的流量脉动很大,不建议采用。

图6 流量脉动系数随着不对称啮合线宽度的变化Fig.6 Variation of flow ripple factor with asymmetric width on meshing line
由式(6)得类型系数Kc为:
称之为修正的类型系数,见表2。

表2 修正的类型系数Tab.2 Corrected type coefficient
由表2 中看出,同等侧隙时,无卸荷槽与高压、低压单侧卸荷槽时的类型系数均相同;无侧隙较有侧隙下的类型系数更大,纠正了有侧隙下单侧卸荷槽类型系数的现有错误。
高压单侧卸荷槽时,业界有人认为因困油腔始终与出口腔相连通,貌似排量应更大。事实上,困油压缩时的确会向出口腔排油,但困油膨胀时也会从出口腔吸油,因排油和吸油量相等,考虑到困油本身压缩和膨胀时的体积变化很小,可以忽略不计,故理论上对输出排量无影响。同理,低压单侧卸荷槽时的情况亦如此。
6 困油容积变化率的计算
在-ε/2 ≤f ≤-(2k-ε)/2 的1 个困油啮合线区间内,由图2~3 可直接得困油容积变化率QT为:
由此说明困油容积变化率仅与侧隙类型k 有关,而与卸荷槽类型y 无关。
且由
得
其中,QT为负时表示处于困油的压缩阶段,QT为正时表示处于困油的膨胀阶段。最大困油容积变化率为:
与现有结果完全一致[21],由此说明压缩与膨胀阶段的最大困油容积变化率相等,只是正负号不同而已。
相对于对称卸荷槽下相同的压缩阶段与膨胀阶段卸荷面积分布[22],不对称卸荷槽下要么压缩阶段的卸荷面积更大或更小,要么膨胀阶段的卸荷面积更小或更大,由此说明不对称卸荷槽时要么压缩阶段的困油现象更严重,要么膨胀阶段的困油现象更严重。总之,不对称卸荷槽下的困油现象更严重。
有侧隙与无侧隙下最大困油容积变化率之比为:
由式(18)和泵用重合度为1.05~1.3,说明无侧隙困油现象更严重。
比起困油容积变化率现行的扫过面积计算方法[17],这种由齿面流量Q0直接得到困油容积变化率QT的原理更清晰,方法更简单。
7 结论
(1)以1.0,0.5 分别表示有、无侧隙的不同类型,双卸荷槽对称线与齿轮副中心线的无量纲不对称啮合线宽度为变量的输出特性公式,简洁可靠。
(2)同等侧隙类型下无卸荷槽与单侧卸荷槽的类型系数均相同;无侧隙较有侧隙的类型系数较小,纠正了有侧隙下单侧卸荷槽类型系数的现有错误。
(3)相比困油容积变化率现行的扫过面积计算方法,由齿面流量直接得到困油容积变化率,方法更简单,原理更清晰。
(4)对称卸荷槽或无侧隙类型下的排量更大,流量脉动更小,不对称卸荷槽较对称卸荷槽、无侧隙较有侧隙类型下的困油现象更严重;无特殊情况不建议使用双卸荷槽不对称设置。
