基于压力分布聚氨酯类睡枕的高度研究
2024-02-27王宜旸王瑞华
王宜旸,王瑞华
(齐齐哈尔大学,黑龙江 齐齐哈尔 161000)
1 任务背景
当前,市面上的睡枕产品种类繁多,但缺乏个性化的适配方案。关于睡枕的舒适性研究还处于初级阶段,仍在研究头部不同区域的舒适度需求差异。由于个体差异显著,不同用户对睡枕的压力分布与支持性需求提出了不同的标准[1],因此,开发一种能精确匹配用户特定需要的智能系统具有重要的理论意义和实践价值。
2 体压分布实验
2.1 仰卧与侧卧时的体压分布
体压分布是评价睡枕支撑舒适度最直观的指标之一。合理的压力分布是保证舒适性的关键,也是睡枕支撑面分区的重要依据。本实验采用仰卧与侧卧两种方式最大限度地还原人体睡眠状态。
2.2 实验器材使用
颈椎曲线测量仪、马丁测量仪、多点融合压力测量系统、手机拍摄支架、数显万能角度尺。
2.3 方案设计
本实验采用聚氨酯材质的睡枕,该睡枕有较好的压缩性能,在施加压力一段时间后,睡枕的压缩率逐渐趋于稳定状态,而后根据受试者的感受反馈,调整睡枕的高度至舒适值。为防止误差,每次实验进行3次测量。受试者分为10组,每组单独进行实验,实验环境为26 ℃,无明显噪声。每次实验由一名受试者参与,分为生理信息收集、颈椎高度测量、压力测量3个阶段。模拟常见的侧卧、仰卧两种睡姿,且至少有两名研究员参与实验模拟记录。
实验前,由研究员进行人员信息登记和项目介绍。待受试者进入模拟实验区后,由研究员进行颈椎曲线及高度测量;实验时,受试者进入模拟睡眠仰卧状态(体验操作开始后40 min)及模拟睡眠侧卧状态(体验操作开始后70 min),研究员不进行干预;实验后,由研究员对受试者进行访谈,并由受试者填写调查问卷及用户体验测评表;实验结束。对于每位受试者的体验过程,均录制视频作为记录。
2.4 受试者招募情况
本研究共招募了10名自愿参与的受试者,基本信息如下:男性5名、女性5名,(25.0±3.8)岁。
2.5 睡枕压力值
体压指数是反映体压分布的物理量,起到了体压测试结果和主观舒适度评价之间的桥梁作用。选择合适的体压指数可以提高客观测试结果和主观舒适度评价结果之间的相关性。本实验选择平均压力和峰值压力作为体压指标,图1中1、2两个区域作为仰卧位压力值测试区域,3、4区域作为侧卧位压力值测试区域,测量数据如表1所示,侧卧位压力测试点由受试者根据个人习惯进行选择。
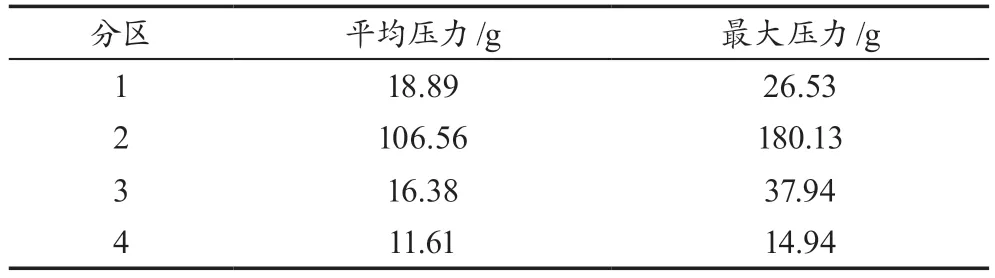
表1 分区体压分布数据

图1 压力测试区域划分
2.6 睡枕压缩后高度测量
根据压力分区的结果,2区域压力值为仰卧时受压最大值。因此,测量仰卧位压力时,选用2区域压缩后的枕高作为参考;测量侧卧位压力时,选用受试者实验时的3区域或4区域压缩后枕高作为参考。本实验测量了受试者使用睡枕时睡枕达到稳定状态后的压缩高度,如表2所示,该高度受试者表示舒适。
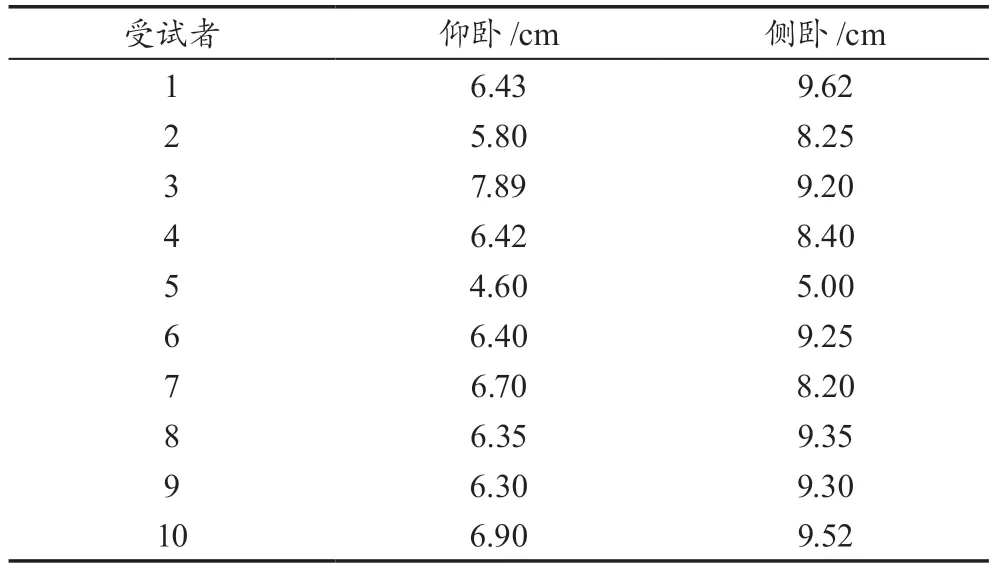
表2 压缩后枕高
3 舒适枕高预测
3.1 基于用户生理信息的舒适枕高预测
本研究在实验前分别收集了受试者的生理信息,包括身高、体重、肩宽、头围、性别等,并使用机器学习下的监督学习方法,对其进行机器学习回归预测。研究采用受试者生理数据作为自变量,舒适枕高作为因变量,采用支持向量机(Support Vector Machines,SVM)与反向传播算法(Back Propagation,BP)神经网络两种方法进行对比得出其机器学习回归模型。
3.2 SVM
SVM可以结合不同的核函数来估计回归,被广泛应用于分类、回归和检测等研究领域。对于回归问题,给定训练样D={(x1,y1), (x2,y2),...,(xn,yn)},本实验希望学习到一个f(x)使其与y尽可能接近,w、b是待确定的参数。在此模型中,只有当f(x)与y完全相同时,损失才为零,而支持向量回归假设能容忍的f(x)与y之间最多有ε的偏差,当f(x)与y的差别绝对值大于ε时,才计算损失,此时相当于以f(x)为中心,构建宽度为2ε的间隔带,若训练样本落入此间隔带,则认为是被预测正确的[2]。
3.3 BP神经网络
BP神经网络是一种多层前馈神经网络,是目前应用最广泛的神经网络模型之一。对于只含一个隐层的神经网络模型,BP神经网络主要分为两个阶段,第一是信号的前向传播,从输入层经过隐含层,最后到达输出层;第二是误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置、输入层到隐含层的权重和偏置[3]。
3.4 建立方法
通过前期实验阶段收集一组包含身高、体重、肩宽、头宽以及对应睡枕高度的数据。
3.4.1 BP神经网络
使用收集到的数据训练一个线性回归模型。线性回归模型会学习这4个特征与睡枕高度之间的线性关系。当输入一个新的用户数据(身高、体重、肩宽和头宽)时,该模型就可以根据训练好的参数预测出该用户适合的睡枕高度。
3.4.2 SVM
同样采用前文提到的数据收集方式,但SVM模型训练的过程不唯一定位于寻找睡枕高度的具体值,而是将其视作二分类问题,即高枕或低枕。在这个例子中,将睡枕高度视为一个回归问题,并使用SVM找到一个最优超平面,使不同类别的数据点尽可能地分开,从而对新用户进行高度分类。当输入一个新的用户数据(身高、体重、肩宽和头宽)时,该模型可以根据训练好的超平面,判断出该用户属于哪一类,即高枕或低枕。
3.5 预测结果
表3展示了交叉验证集、训练集和测试集的预测评价指标,通过量化指标衡量支持向量回归的预测效果。
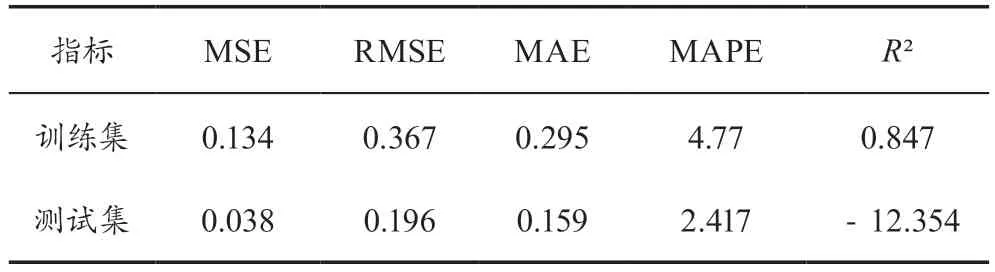
表3 支持向量机(SVM)
表4展示了3个SVW的预测结果与真实值的差异。
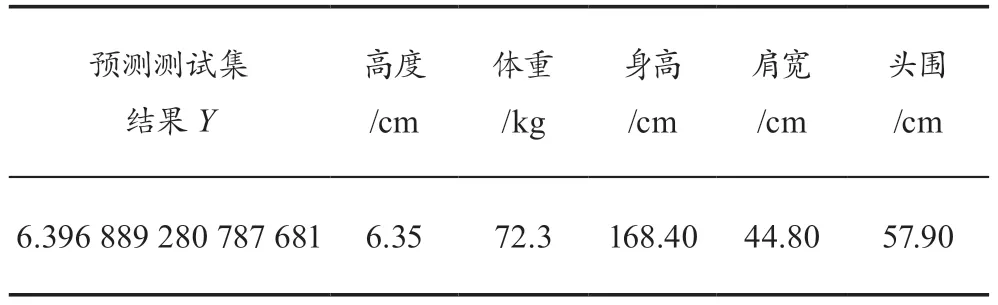
表4 SVM预测结果
表5展示了交叉验证集、训练集和测试集的预测评价指标,通过量化指标衡量BP神经网络回归的预测效果。
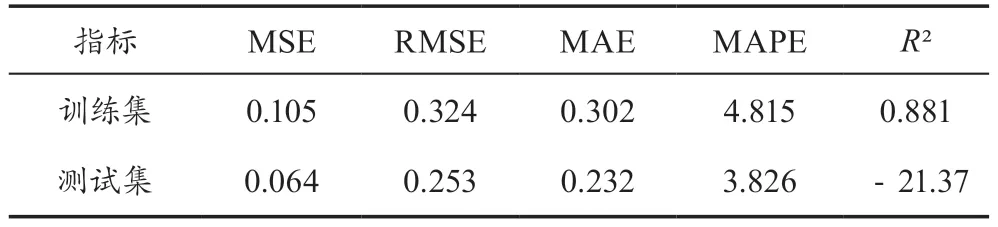
表5 BP神经网络
表6展示了BP神经网络预测结果与真实值的差异,其中,表3与表5中的均方误差(MSE)是指预测值与真实值之间偏差的平方和的平均值,其值越接近零,表明模型的预测准确性越高。均方根误差(RMSE)是均方误差的算术平方根,同样,其值越小,说明模型的预测性能越优越。平均绝对误差(MAE)计算了预测值与真实值之间的差异的均值,较小的MAE数值代表更高水平的模型精度。平均绝对百分比误差(MAPE)是MAE的百分比形式,表示误差的平均百分比,当MAPE的值减小时,模型的准确度就提升了。决定系数(R²)描述了模型预测值与实际数据平均值相比的拟合程度,R²值越接近1,代表模型具有更高的解释性和预测准确性。
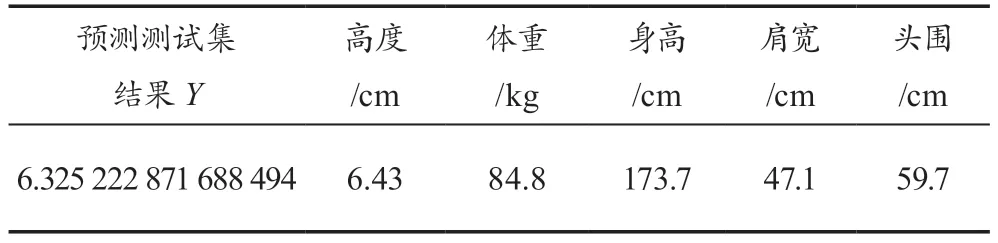
表6 BP神经网络预测结果
由此可见,SVM准确率略高于BP神经网络回归(图2)。此回归模型可用于协助相关企业根据用户生理信息精确生产,为用户提供精确的睡枕定制数据。

图2 真实高度与两种预测方法对比
4 结论
(1)通过人体压力分布实验,可以得到舒适度匹配度最高的10个样本的平均压力分布矩阵,从而得到其合适的睡枕高度;与理想枕高相似度可以在一定程度上有效表征舒适性评价。
(2)通过机器学习与深度学习两种方法,分别对仰卧及侧卧两种睡姿的舒适枕高进行回归模型建模,并对比其准确率,有助于找到一种有效的方法,帮助相关企业根据用户生理信息精确生产枕高适合用户的睡枕。
(3)将睡枕区域进行划分,测量其压力值,得到仰卧位2区域压力值最大。因此,在设计相关产品时应考虑减少该分区的压力负荷,以改善产品体验。同时,此压力值也可用于对后续产品的改进,帮助设计师设计新产品后对其产品舒适度进行评价。
