基于IMOCS-BP 神经网络的锂离子电池SOH 估计

王 雪（中国电源学会学生会员），游国栋，房成信，张 尚

（天津科技大学电子信息与自动化学院，天津 300222）

锂电池具有使用寿命长、环保等优点，是储能系统的基础[1]。储能系统的管理是近年的研究重点，健康状态SOH（state-of-health）是能够反映储能系统工作状态的重要指标。储能系统的SOH 受到最大可用容量、电量、电压、电流和荷电状态SOC（state-of-charge）等参数的影响[2]。因此，为了能够直观地观测到电池状态，有力保障储能系统的安全和正常运行，SOH 的精准预测是不可或缺的。目前SOH 预测方法分为4 类：基于模型的方法[3]、数据驱动方法[4]、混合方法[5-6]和其他方法[7]，从这4 个方面全面地概述了当前SOH 预测研究的现状。传统的数学建模估算电池寿命方法受各种外界条件的影响，精度难以保证，不能准确地评估其SOH。随着智能算法的快速发展，基于数据驱动的方法也有了很大程度的提升。越来越多的方法借助机器学习算法对历史数据进行学习而不是依赖于电池内部的电化学原理，通过训练好的模型对SOH 进行估计。文献[8]利用传统的BP 神经网络对SOH 进行估算，但是采用最速下降法，导致陷入局部最优和收敛速度慢的问题。文献[9]利用SA 算法对BP 神经网络的权值进行优化，避免陷入局部最优的困境，但是并没有对阈值进行优化，降低其对算法的影响。

为了解决BP 神经网络算法容易陷入局部最优的问题，本文针对神经网络多节点的特点应用改进的多目标布谷鸟搜索IMOCS（improved multi-objective Cuckoo search）算法，对各节点的初始参数进行优化，减小陷入局部最优的可能。由于多目标布谷鸟搜索MOCS（multi-objective Cuckoo search）算法与传统单目标搜索算法区别只是将目标空间拓展到了多维空间，并未摆脱传统CS 算法收敛速度慢、求解精度低等问题。为解决这些问题，改变MOCS算法中的更新概率及搜索步长，在保证求解精度的同时加快收敛速度，同时保留布谷鸟搜索算法全局搜索最优参数的优点。

1 电池健康状态估计模型

电池的SOH 只能通过其他方法利用电池在工作状态下产生的各种参数估算得到SOH 的预测值。利用估算方法对SOH 精准预测，可以随时了解电池性能的衰退情况和剩余使用寿命，并及时提示用户更换报废电池[10]。同时，SOH 的准确预测也能补偿由于老化程度带来的SOC 预测误差，提高SOC 预测结果的精度[11]。电池SOH 估算的常用方法包括健康因子提取法、模型参数辨识法及多模式混合的方法。通常情况下，SOH 用容量法表示，其计算公式为

式中：Ci为第i 个充放电周期的最大可用容量；C0为初始最大可用容量。

2 IMOCS-BP 神经网络算法

2.1 IMOCS 算法

BP 神经网络通过微分传递实现非线性映射，通过前向传输信号和反向传输误差进行不断地自我学习来调整权值和阈值，适应不断变化的外部环境[12]。BP 神经网络具有输入层、隐含层和输出层，其拓扑结构如图1 所示。BP 神经网络的权值及阈值是随机赋值初始化，在训练时不能以较快的速度达到理想的预测效果并且易陷入局部最优解。针对上述问题，本文引用IMOCS 算法对BP 神经网络初始的权值与阈值进行优化。

图1 BP 神经网络Fig.1 BP neural network

MOCS 算法是将CS 算法扩展到多维空间，在继承了CS 算法全局搜索能力强、参数少、易实现等优点[13]的同时仍受到CS 算法的影响，致使收敛速度较慢。CS 算法的基本思想源于鸟类的莱维非高斯随机飞行行为和布谷鸟的繁殖特征。在个体飞行中，交替呈现短距离小步长和长距离大步长，这可以避免算法落入局部最小值[14-15]。所有个体位置的更新过程为马尔可夫链MC（Markov chain）过程，表示为

式中：Iiter和Iitertotal分别为当前迭代次数和总次数；αIiter和αIiter+1分别为当前和下一代自适应步长因子；a 为影响系数；为2 次迭代函数的变化趋势。改进后的位置更新过程为

发现鸟蛋概率为设定值。一般来说，布谷鸟算法会设置发现鸟蛋产生新解的概率pa=0.25，但在后期可能会造成丢失优质解，影响算法收敛效率及精度。为了避免优质解丢失对算法造成影响，应对概率pa做出调整，同上，即在前期取较大值，随着优质个体解的产生而降低pa的值，保证算法的收敛速度，则有

式中，pamax、pamin为控制参数。

2.2 基于IMOCS-BP 神经网络的锂离子电池健康状态估计

基于IMOCS-BP 神经网络使用改进后的MOCS算法全局搜索BP 神经网络各节点空间，在IMOCS算法迭代结束搜索到的全局最小值的基础上优化各节点初值，转而采用梯度下降法进行精确搜索，步骤如图2 所示。

图2 基于IMOCS-BP 神经网络的锂离子电池健康状态估计步骤Fig.2 Steps in SOH estimation of lithium-ion battery based on IMOCS-BP neural network

具体算法如下：

（1）读取输入输出数据xinput、xoutput。

（2）设置鸟窝（节点）个数n，设置BP 网络的输入节点数ninput、隐含层节点数nhidden及输出节点数noutput，构建网络Φnet。

（3）对训练集xinput_train、xoutput_train与测试集xinput_test、xoutput_test归一化后，得到xinputn、xoutputn。

（4）设置更新概率的控制参数pamax、pamin。

（5）将鸟窝个数n，网络结构参数ninput、nhidden、noutput，网络Φnet，归一化后参数xinputn、xoutputn作为输入参数，利用IMOCS 算法进行优化。

（6）设置全局搜索下限nd，设置总迭代次数Iitertotal，通过IMOCS 算法得到优化后的最优初始权值与阈值θbestnet。

（7）将优化后的最优初始权值与阈值θbestnet赋予BP 神经网络。

（8）选择传递函数：一般来说BP 神经网络中隐含层的传递函数均选择sigmoid 函数，输入可取任意值，而输出为0～1。传统sigmoid 函数对数据进行中心化处理时会使数据平均值接近于0.5，而tansig 函数输入可取任意值，输出则在-1～1 之间，则会使其数据平均值更接近于0。因此除了在二元分类情况下使用sigmoid 函数性能较好外，tansig函数的适用度及性能更高。因此隐含层采用tansig函数作为传递函数，输出层仍采用线性传递函数purelin 函数g（y）=y。

（9）将电池数据样本分为训练集与测试集，以前段数据作为训练集对算法进行训练，用后段测试集数据进行预测和对比。

3 仿真及分析

3.1 仿真数据

本文采用NASA 的电池实验测试数据，分别进行BP 神经网络、MOCS-BP 神经网络和IMOCS-BP神经网络的SOH 预测仿真。选取3 组锂离子电池通过充电、放电、阻抗检测运行，充电方式相同且均以1.5 A 的恒定电流充电至电池电压达到4.2 V，以2.0 A 的电流进行放电，直到5#、6#、7# 电池电压分别在2.7、2.5、2.2 V 停止，最后通过阻抗测量获取电池内部参数，电池数据如图3 所示。随着锂电池充放电次数的增加，其内部的温度和内阻变化逐渐剧烈，实际的SOH 值变化具有非线性和波动性，不是简单的衰退，图3 也验证了这一现象。

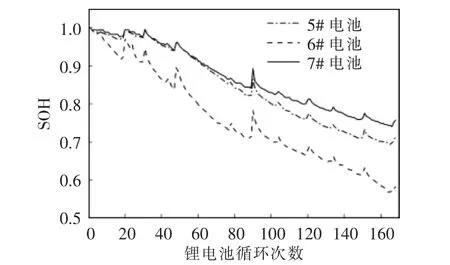
图3 NASA 电池测量数据Fig.3 NASA battery measurement data

由于锂电池的SOH 受多因素影响，不能直接测量，因此需要健康因子HI（health index）来表征出SOH 的变化。一般来说，最直观观测锂电池性能下降的特点是容量下降，以容量变化作为直接HI最为准确。而在实际测量容量时通常是采用破坏性入侵测量，难以实现SOH 的在线应用，因此，本文算法的输入是以充放电电压、充放电电流及循环次数构成的间接HI，算法的输出，以容量法定义的SOH 构成。对5#、6#、7# 这3 组电池数据分别采用BP、MOCS-BP 及IMOCS-BP 算法进行仿真，将数据分为前后两段分别用于训练与测试。

3.2 评价指标

本文选取均方误差MSE（mean square error）、平均绝对误差MAE（mean absolute error）与平均相对误差MAPE（mean absolute percentage error）3 个指标对上述3 种算法进行性能评估。3 个指标计算公式分别为

值得注意的是，MAPE 的范围为[0，+∞），MAPE越趋于0 表示模型性能越强；反之，MAPE 越大表示模型性能越差；当MAPE 大于100%时可以认为该模型为劣质模型。

3.3 仿真设计

3 种SOH 估测算法的参数设置如下。

对BP 神经网络的参数进行设置时，其性能易受到隐含层数的影响。针对隐含层设置问题，可参考经验公式

式中：Mnum为隐含层节点数；Min为输入层节点数；Mout为输出层节点数；b 为0～10 之间的常数。故本文隐含层数应选择2～12。本文针对不同层数的隐含层BP 神经网络，使用MSE、MAE 和MAPE 进行性能评价，最终选择性能最强的4 层隐含层BP 神经网络与另外2 种方法进行对比，评价结果如表1所示。

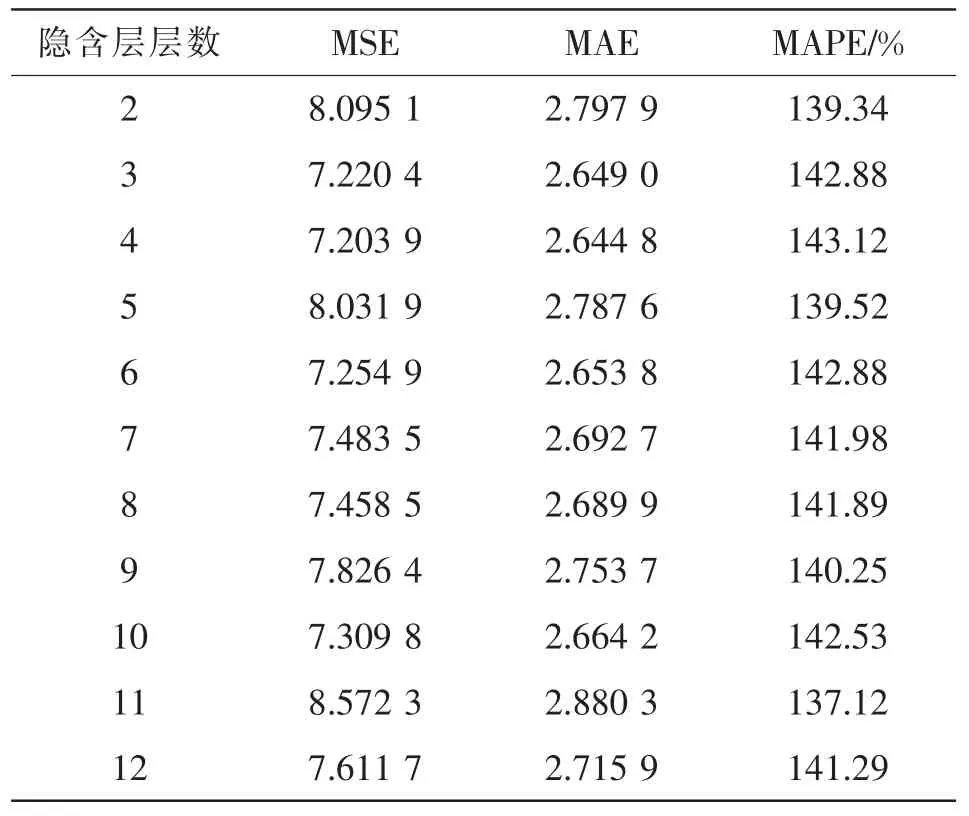
表1 不同隐含层层数的BP 神经网络评价指标Tab.1 Evaluation indexes for BP neural network with different numbers of hidden layers

使用传统MOCS-BP 算法时，通过对不同参数下实验结果的研究发现，将隐含层设为3 层时效果较好。建立的BP 神经网络结构为5-3-1，由此可以确定要优化的BP 神经网络权值与阈值的个数：权值个数为5×3+3×1=18，阈值个数为3+1=4，因此MOCS 算法和IMOCS 算法均要对该神经网络结构的22 个参数进行优化。在算法运行过程中将对上述参数进行多次更新，将多次迭代后得出的最优权值与阈值赋予为BP 神经网络初始的权值与阈值，实现BP 神经网络对SOH 的预测。由多次实验的最佳效果确定：宿主随机抛弃鸟蛋的概率pa=0.25、鸟巢数量n=25、全局搜索下限nd=22、迭代次数Iitertotal=100。

与MOCS-BP 算法不同的是，IMOCS-BP 算法需要另外设置pamax=0.5，pamin=0.1。

3.4 仿真结果与分析

利用3 组电池数据的测试集，分别对上文3 种方法的预测效果进行检验，算法预测效果如图4、图5、图6 所示。

图4 BP、MOCS-BP 与IMOCS-BP 算法对5#电池SOH 的预测Fig.4 SOH prediction of No.5 battery by BP,MOCS-BP and IMOCS-BP algorithms

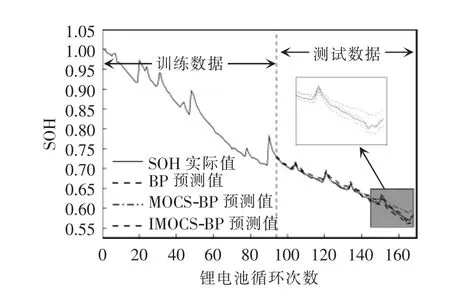
图5 BP、MOCS-BP 与IMOCS-BP 算法对6#电池SOH 的预测Fig.5 SOH prediction of No.6 battery by BP,MOCS-BP and IMOCS-BP algorithms

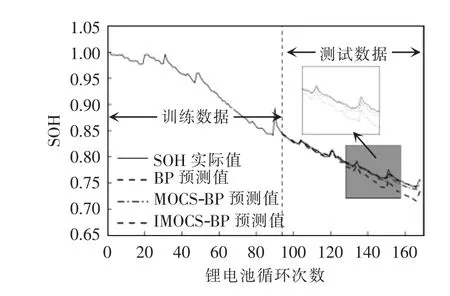
图6 BP、MOCS-BP 与IMOCS-BP 算法对7#电池SOH 的预测Fig.6 SOH prediction of No.7 battery by BP,MOCS-BP and IMOCS-BP algorithms

5# 电池3 种SOH 预测算法的误差如图7 所示。由图可见，基于BP 神经网络预测误差最小值为1.8，并随着迭代次数增加而升高；2 种布谷鸟优化算法的预测误差大大降低，且不会随着迭代次数的增加而出现较大波动，其中：MOCS-BP 算法的SOH误差范围为-0.012～0.004，IMOCS-BP 算法的SOH误差进一步缩小，处于-0.011 0～0.003 8 之间。

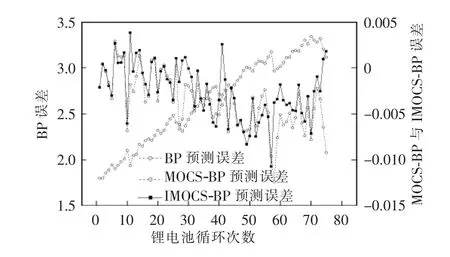
图7 BP、MOCS-BP 与IMOCS-BP 算法的预测误差对比Fig.7 Comparison of prediction errors among BP,MOCS-BP and IMOCS-BP algorithms

针对上述3 种算法，利用评价指标进行性能评价，结果如表2 所示。

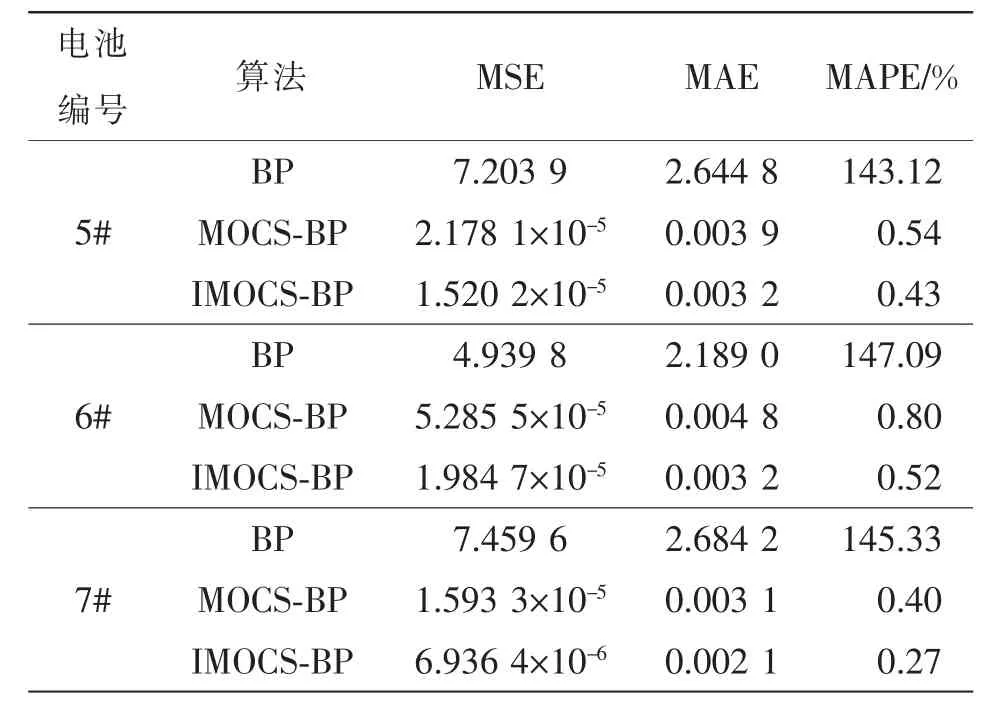
表2 算法评价指标Tab.2 Evaluation indexes for algorithms

综上，IMOCS-BP 神经网络算法的误差更低、性能更好，满足储能锂电池的预测要求。

4 结论

针对BP 神经网络预测锂电池SOH 算法易陷入局部最优的现状，本文提出了一种基于IMOCSBP 神经网络的锂电池SOH 预测方法，将传统布谷鸟算法中确定的概率和随机的步长改为自适应概率与自适应步长，在保证搜索精度的同时提升了算法的效率。使用Matlab 对SOH 预测算法进行仿真验证，结果表明，IMOCS-BP 神经网络算法实现了更好的预测效果，具有更好的性能，能够有效地适应具有非线性特点的锂离子电池。应用片段历史数据对锂电池SOH 进行预测，实现了在线估计，具有实际的应用价值。

本文未将温度、内阻和自放电速率等因素加入研究中，下一步工作将尝试如何将这些因素加入并建立准确度高、适用性强的HI 提取方法。