盾构隧道下穿城市道路的路面沉降计算方法研究
2024-02-26谢家化林宇亮
张 杰,马 野,谢家化,林宇亮
(1.中铁隧道局集团有限公司,广东广州 511458;2.中南大学土木工程学院,湖南长沙 410075;3.中铁第六勘察设计院集团有限公司,天津 300308)
0 引言
在城市地下空间的开发与利用过程中,涌现出大量的新旧线路交叉问题,成为制约该地区基础设施建设体系升级发展的关键节点。为加快区域内现代化产业体系发展,处理线路交叉工程问题,建设城市地下隧道成为重要解决途径(Zhou et al.,2023)。地下隧道常采用盾构法进行施工。隧道衬砌一般由隧道管片拼装而成,作为永久性结构能够承受施工及运营阶段的外部荷载。隧道管片主要为钢筋和混凝土组合而成的材料,但传统有筋混凝土管片抗拉性能较差,在生产、施工和运维等过程中容易出现管片破损、开裂等问题(邓一三等,2022)。钢纤维混凝土管片是在普通混凝土内掺入一定量各向分布的钢纤维可浇筑成型的新型复合构件,相比于普通的混凝土管片具有更为优异的抗裂性能和耐久性(张帆等,2023)。与此同时,纯钢纤维混凝土管片在减少工程用钢量,缩短施工周期以及降低运维期维修成本等方面具有明显的经济效益。目前我国纯钢纤维混凝土管片的研究还不完善,特别是盾构隧道下穿既有城市道路,势必会扰动地下岩土体引发地面变形。针对新型的隧道管片结构和独特的下穿施工方式,研究与之相适应的土体位移计算方法是相对迫切且重要的研究内容。
盾构施工的本质是一种全自动机械化暗挖方法,而施工过程是在土体内部进行的,势必会扰动地下土体,迫使初始应力场发生变化,应力的变化由内向外发展到地表并引起变形(Ropkins and Allenby,2004;Yang and Wang,2011)。目前国内外计算土体变形的方法主要有工程实测法、经验公式法、理论解析法、随机介质法和数值模拟等。在工程实测方面,国内外学者对平行隧道、地铁隧道穿越污水管、隧道下穿路堤、矩形顶管等工程进行监测、归纳分析与研究(Hnasmier and Gutter,1998;王斌等,2010;邓长茂等,2016;李明宇等,2019;司金标等,2019)。传统的经验公式法视沉降槽曲线符合正态分布特征并给出估算公式(Matros,1958;Peck,1969)。后续学者对Peck公式进行了不同程度的修正,但仍存在较大不足(Attewell,1974;Atkinson and Potts,1977;陈春来等,2014;魏纲和王霄,2017)。基于隧道间隙理论,针对浅埋隧道采用经验公式估算土体变形存在较大误差(Lee et al,1992;韩煊和李宁,2007)。解析法采用椭圆形土体移动平面推导出不排水条件下由隧道开挖引起的土 体 位 移(Sagaseta,1987;Schmidt,1988;Verruijt and Booker,1996;Loganathan,1998)。但 是 以Loganathan法为代表的解析法计算曲线形状时受隧道埋深和隧道开挖半径影响较大,在浅埋、大断面条件下预测地表沉降适用性较差。随机介质理论方法是在研究采煤工程引起的地表移动时,经过砂箱模型试验和数学推导建立的理论思想(刘宝琛和张家生,1995;张府等,2019)。随机介质理论可用于预测近地表开挖而引起的土体变形,并不受埋深和结构尺寸的限制。在下穿施工引起地表沉降变形的研究中,数值模拟方法运用较多(杨转运,2008;黄生根等,2009;黎永索,2011;喻军和龚晓南,2014)。但模拟中土体参数的选择、模型的构建和分析结果的处理存在差异性和不确定性。
为探究澳门纯钢纤维管片盾构隧道施工引起友谊大马路面工程变形的分布情况及演化特征,借助弹性力学方法及随机介质理论等手段进行研究,提出适用于有重无水作用下浅埋隧道下穿施工引起土体位移计算的理论方法,并与现场实测值进行对比分析。该研究结果可为盾构施工土体变形预测、地下空间安全评估、路基的稳定性维护和精细化控制等方面提供重要的研究思路。
1 隧道施工引起土体变形计算
1.1 计算模型
统计分析国内外已有的下穿既有公路工程中路面沉降变形数据,绝大部分下穿公路工程在施工过程中引起土体变形影响规律相近,并不受施工方法、隧道类型,公路等级等因素的影响。故可结合盾构隧道自身特点,借鉴弹性力学平面模型与应力函数解法,在平面应变条件的条件下,推导出浅层纯钢纤维管片隧道周围土体变形的计算公式(Chou and Bobet,2002;Zhang et al.,2018)。盾构隧道施工引起土体变形问题是三维的,但在平衡状态下土体的应变只在某一个平面内发生变化,沿垂直于该平面的方向没有变化,在数学上可以简化为二维平面模型求解。其中,浅埋隧道的解必须满足平衡方程、应变相容方程和边界条件,其计算简图如图1所示。
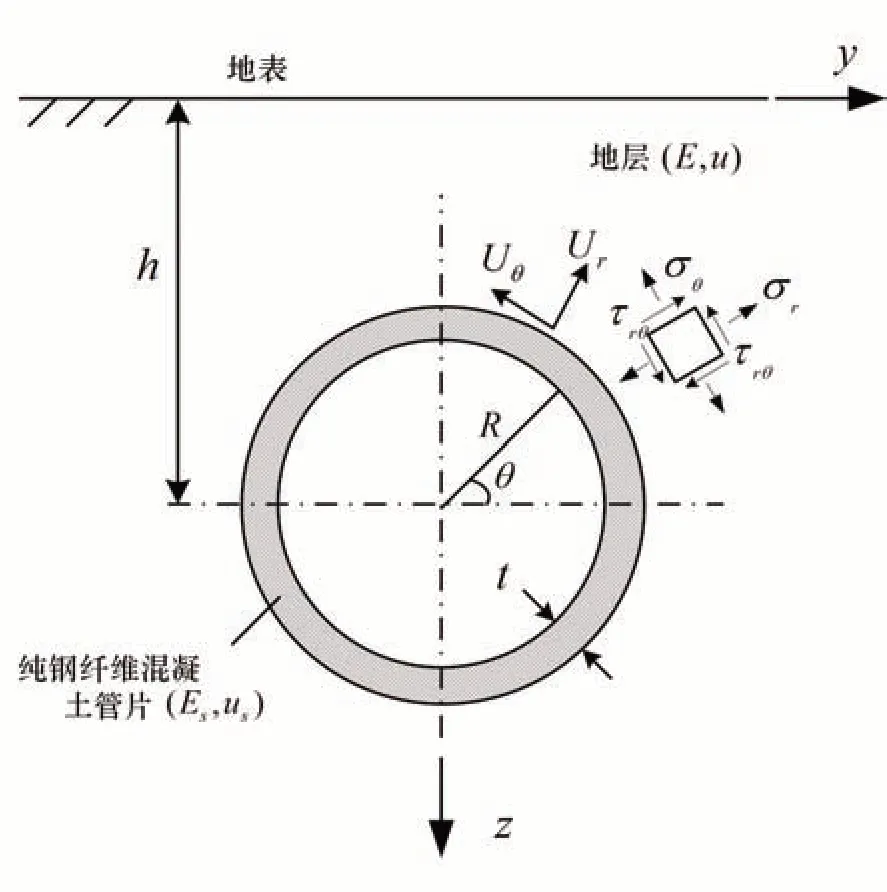
图1 浅埋隧道计算模型Fig.1 Calculation model of shallow buried tunnel
平衡方程可以采用在弹性力学理论中提出的适用于浅埋隧道的一般应力函数(Timoshenko and Goodier,1970;项彦勇,2014)。其在rθ极坐标系下,表达式如下:
式中:a0,b0,c0等是由边界条件确定的参数。
1.2 边界条件
计算模型中,垂直于隧道横截面方向应满足平面应变条件。土体视为均质土、各向同性且满足弹性假定,隧道与土体之间摩擦系数足够小且可产生滑移,如图2所示。

图2 有重无水浅埋隧道边界条件Fig.2 Boundary conditions of heavy anhydrous shallow tunnel
边界条件由两个部分组成:隧道开挖边界处,面力等于零;在距离隧道足够远处,应力等于地层自重应力。由此,构建平衡方程边界条件为:
式中:σ、τ、U为极坐标系下应力和位移,g为等效间隙参数,γ为土的容重,h为隧道埋深,k为土压力系数。
1.3 相容方程
盾构隧道下穿工程中,一般隧道上覆土较薄且不受地下水的影响。隧道和土体协同变形,应满足应力应变相容方程:
当满足管片厚度t远小于隧道半径R时,压缩系数C和柔度F为:
式中:E,u为土层的弹性模量和泊松比,Es、us为钢纤维混凝土的弹性模量和泊松比,As为管道截面积Is管道惯性矩,R为隧道半径。
综合应力平衡方程式(1)、边界条件式(2)和应变相容方程式(3),可对隧道径向位移Ur和隧道环向位移Uθ进行求解:
式中:a0、c1、c1′、d1′、a2′、b2′、c3′,d3′参数满足下列方程:
式中:E、u为土层的弹性模量和泊松比,g为等效间隙参数,γ为土的容重,h为隧道埋深,k为土压力系数,R为隧道半径,Z为垂直向下的距离,y为距离轴线的水平距离。
为将rθ极坐标位移转换为笛卡尔坐标位移,可利用如下关系:
由此,可以得到笛卡尔坐标下的水平位移Uy和沉降Uz。
考虑到隧道与土层材料参数差异较大取C=0且F→∞,代入公式(9)得:
1.4 随机介质法
随机介质理论基本思想:在假定土体不排水固结、密度不变化、岩土体不可压缩条件下,将整体开挖对土体沉降的影响分解为无限个小开挖影响的总和。经过后期的不断完善、在平面应变条件下,坐标(ξ,η)的微单元的开挖引起地表某点(x, 0)的沉降大小为S(x, 0),即:
式中:S(x, 0)为横坐标x处的地表沉降量,Ω为沉降区域,β为隧道上部围岩主要影响角。
基于随机介质理论,盾构隧道下穿施工过程中,存在均匀收敛和不均匀收敛两种计算模式(韩煊等,2007),如图3所示。均匀收敛模式下,隧道悬浮于减阻泥浆套中,隧道顶部间隙等于底部间隙。而不均匀收敛模式下,隧道下沉,没有底部间隙。
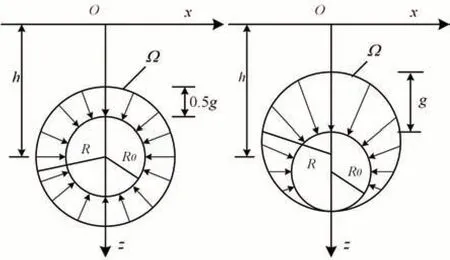
图3 开挖断面收敛模式Fig.3 Convergence patterns of excavation sections
结合图3,推导出盾构施工引起的土体位移公式,在已知盾构隧道半径为R,埋设深度h,土体损失率ε0和土体间隙等参数时,可以求出地表水平位移分布规律。
均匀收敛模式下,土体竖向沉降的计算公式:
不均匀收敛模式下,土体竖向沉降的计算公式为:
式中:ξ和η为计算微元的长和宽;β为隧道上部围岩主要影响角。其他符号计算如下:a=h-R,b=h+R,c=-(R2-(h-η)2)0.5,d=(R2-(h-η)2)0.5,a1=h-R+0.5g,b1=h+R-0.5g,c1=-((R-0.5g)2-(h-η)2)0.5,d1=((R-0.5g)2-(h-η)2)0.5,a2=h-R+g,c2=-((R-0.5g)2-(h+0.5g-η)2)0.5,d2=((R-0.5g)2-(h+0.5g-η)2)0.5。
2 实例验证
2.1 工程实测
澳门新口岸区污水截流管隧道为单线盾构隧道,临近澳门教科文中心、下穿友谊大马路,全长约2260 m,隧道埋设深度为7.5 m。钢纤维混凝土外径为3.2 m,管片厚度为0.2 m。为保证盾构施工安全和周边建筑物稳定,在盾构施工影响范围内,布置监测点进行工程监测。如图4所示,布置地表沉降观测点11个,间距2 m×2 m埋设沉降钉,采用水准仪和经纬仪对公路沉降和水平位移进行观测且按照二等测量要求操作。土体测斜管1个,深度30 m。
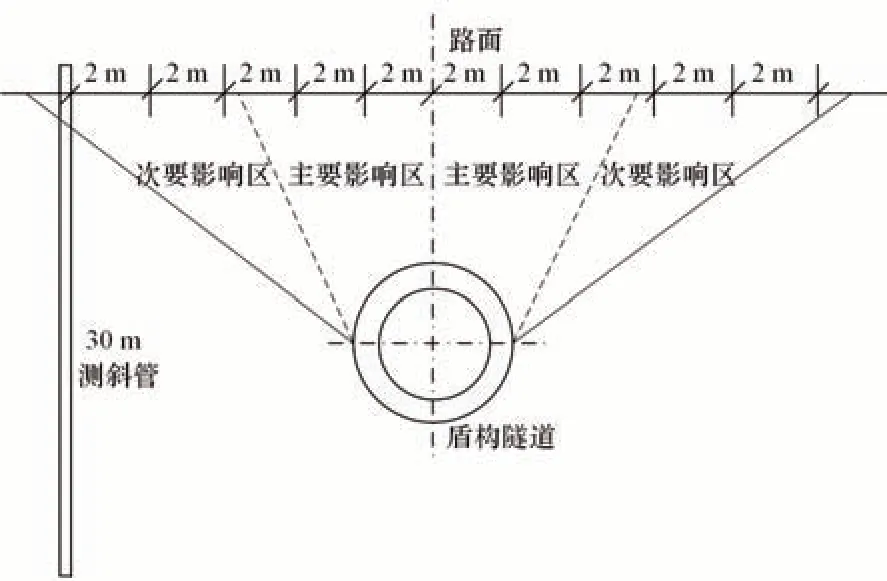
图4 工程监测点布置Fig.4 Layout of engineering monitoring points
2.2 对比分析
依托澳门新建污水管道下穿友谊大马路工程实例,对纯钢纤维混凝土管片盾构施工引起的土体变形进行对比计算。结合招标地质文件及地质补勘资料,场地土层主要为:0~2 m人工填土、2~5 m中粗砂土层,5~8m淤泥质土层,7~15 m为花岗岩。隧道施工范围主要涉及淤泥、黏土层。按等代法原理计算土体参数,综合取土层模量E=14.5 MPa,容重γ=18.8 kN/m3,间隙参数g=40 mm,泊松比u=0.25,上部围岩影响角度β=25°,取土体损失率ε0=0.2%。
图5为澳门盾构隧道下穿公路工程引起的地表横向沉降曲线结果。实测值与本文所提出的法计算结果比较吻合。其中,实测值最大沉降量为9 mm,本文所提出的方法最大计算沉降值为8.5 mm,误差值为5.5%。而随机介质法-均匀收敛模式下最大值为12.5 mm,小于不均匀收敛模式下最大值为13.8 mm,相对误差较大。不均匀收敛模式下,地表沉降槽宽度略小于均匀收敛模式下的计算结果。弹性力学方法,存在假设条件限制,实际土层分布异常复杂,沉降槽宽度大于实际沉降槽宽度。

图5 澳门盾构隧道工程地表沉降曲线Fig.5 Surface settlement curves of the Macao shield tunnel project
图6为澳门盾构隧道下穿公路工程项目距离隧道轴心水平距离10 m处,不同深度下的水平位移曲线。弹性力学方法与实测值能够很好地印证,相对误差为22%。在地表处,两者水平位移相差不大,分别为4.1 mm和2 mm。最大水平位移出现在盾构隧道埋高度处,水平位移峰值为6 mm。随着土体深度的增加,理论计算值略大于同一埋深下水平位移实测值。

图6 澳门盾构隧道工程水平位移曲线(x=10m)Fig.6 Horizontal displacement curves of the Macao shield tunnel engineering(x=10m)
3 影响因素分析
3.1 深径比的影响
相比于传统的随机介质理论,本文方法可计算深层土体水平位移。下穿市政道路工程中,盾构隧道往往具备“浅埋、大断面”的特点,埋深和隧道半径对地表沉降产生较大影响。为研究埋深与尺寸的比值对地表沉降的影响,保持埋深为7.5 m不变,改变半径R的大小,形成不同的深径比h/R,计算结果如图7~8所示。在相同的条件下,当增大埋深与隧道半径的比值时,路面沉降槽曲线由“深而窄”向“浅而宽”发展,路面最大沉降值和深层土体水平位移均逐渐减小,沉降槽宽度不断扩大。随着埋深与半径的比增大对土体变形的影响程度不断衰减。
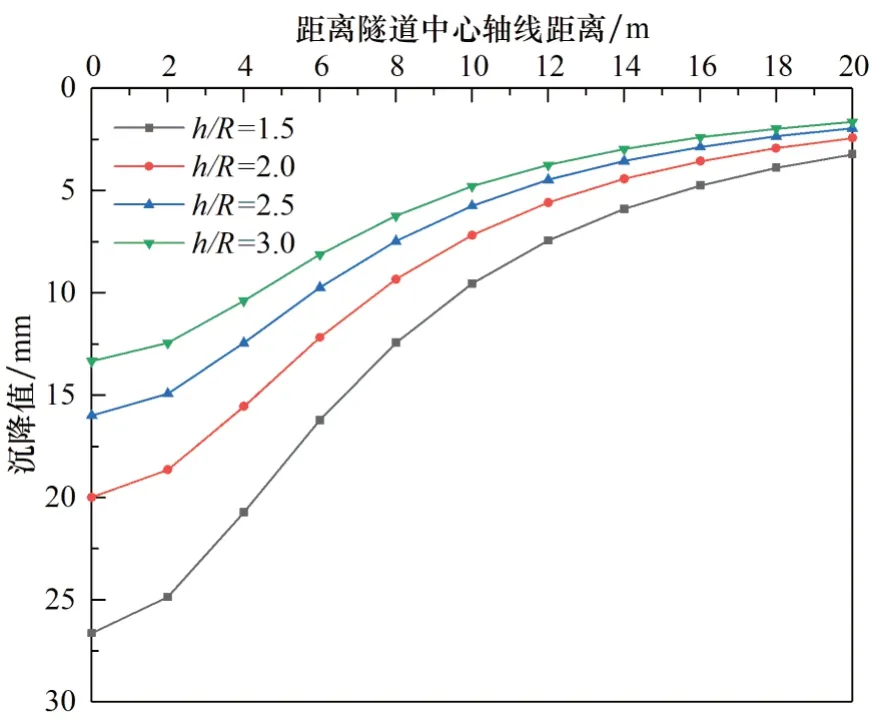
图7 不同深径比的地表沉降曲线Fig.7 Surface settlement curves for different depth to diameter ratios
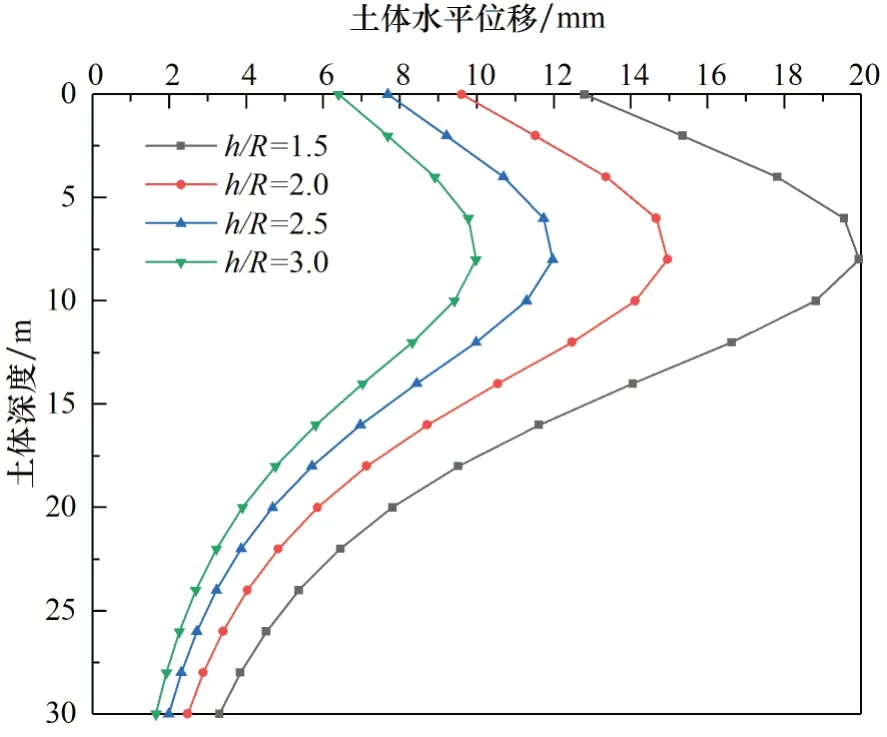
图8 不同深径比的土体横向位移(x=10 m)Fig.8 Lateral displacement of the soil for different depth to diameter ratios (x=10 m)
3.2 间隙参数的影响
在实际工程中,盾构隧道下穿引起的土体间隙往往取决于隧道尺寸和施工技术水平。为探究间隙参数的影响,保持实例中隧道尺寸和地层损失率不变,改变不同间隙参数,计算结果如图9~10所示。随着间隙参数的增大,对应的地层损失总量相应增大,沉降槽曲线整体下移。深层土体水平位移也在不断增大,在隧道埋深附近土体位移变化更为明显。

图9 不同间隙参数的地表沉降曲线Fig.9 Surface settlement curves for different clearance parameters

图10 不同间隙参数的土体横向位移(x=10 m)Fig.10 Lateral displacement of the soil for different clearance parameters (x=10 m)
3.3 土压力系数的影响
保持实例中其他参数不变,调整土压力系数对盾构施工引起的土体变形进行分析。不同土压力系数对地表土体沉降和土体横向位移影响并不显著,为了获取不同土压力系数影响规律,将相对位移变化放大,绘制图11~12。随着土压力系数的增大,地表沉降有向隆起发展的趋势。对应的深层土体位移同步增大,但沿深度方向水平位移变化趋势相同,即最大土体位移出现在隧道埋深处且随着埋深不断减小。
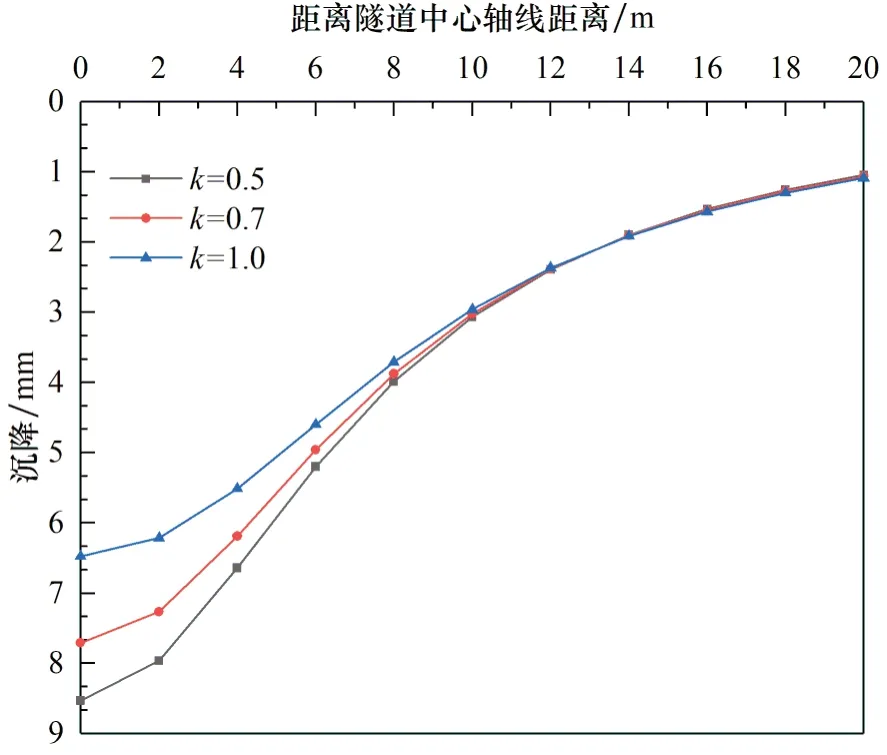
图11 不同土压力系数的地表沉降曲线Fig.11 Surface settlement curves for different earth pressure coefficients

图12 不同土压力系数的土体横向位移(x=10m)Fig.12 Lateral displacement of soil for different earth pressure coefficients (x=10m)
4 结论
基于弹性力学理论,构建了纯钢纤维混凝土盾构隧道下穿施工引起路面沉降预测公式。对比分析了随机介质理论与文中方法的差异性,结合实测数据探讨了不同收敛模式,对土体沉降的影响,获得了如下结论:
(1) 在澳门盾构隧道工程中,弹性力学理论和随机介质理论,两者计算结果呈现的规律相似,在盾构隧道下穿施工引起地表沉降计算较为合理。
(2) 随机介质法理论方法受隧道埋深和隧道尺寸的影响较大,计算精度较差。弹性力学方法预测的最大沉降值偏小,沉降槽宽度偏大。在计算深层土体水平位移上,优于随机介质法。
(3) 与实测数据的对比表明,本文方法的计算参数简单,受土压力系数、土体弹性模量影响较小,适用范围广泛。特别为纯钢纤维混凝土管片结构下穿施工诱发土体变形预测提供了理论依据,也为地下空间安全评估提供了技术支撑。
[附中文参考文献]
陈春来, 赵城丽, 魏纲, 丁智.2014.基于Peck公式的双线盾构引起的土体沉降预测[J].岩土力学, 35(8): 2212-2218.
邓一三,李德明,陈代秉.2022.钢纤维混凝土管片顶推工况下的力学响应试验[J].重庆交通大学学报(自然科学版), 41(8):127-133.
邓长茂, 彭基敏, 沈国红.2016.软土地区矩形顶管施工地表变形控制措施探讨.地下空间与工程学报, 12(4): 1002-1007.
韩煊, 李宁, Jamie R S.2007.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学, 28(1): 23-28,35.
韩煊, 李宁.2007.隧道施工引起地层位移预测模型的对比分析[J].岩石力学与工程学报, 26(3): 594-600.
黄生根, 张健, 张晓炜.2009.超大型箱涵顶进引起的地层位移规律研究[J].岩土力学, 30(2): 387-392.
黎永索, 张可能, 黄常波, 李钟,邓美龙.2011.管幕预筑隧道地表沉降分析[J].岩土力学, 32(12): 3701-3707.
李明宇, 王松, 张维熙, 吴鹏.2019.大断面矩形顶管隧道施工引起的地面沉降分析[J].铁道建筑, 59(5): 81-84.
刘宝琛, 张家生.1995.近地表开挖引起的地表沉降的随机介质方法[J].岩石力学与工程学报, 14(4): 289-289.
司金标, 朱瑶宏, 季昌, 周顺华.2017.软土层中类矩形盾构掘进施工引起地层竖向变形实测与分析.岩石力学与工程学报, 36(6):1551-1559.
魏纲, 王霄.2017.基于统一解的近距离双线平行盾构地面沉降计算[J].现代隧道技术, 54(2): 87-95.
王斌, 陈帅, 陶柏峰, 谭昊.2010.顶管穿越路堤实测地基变形和扰动程度分析[J].岩石力学与工程学报, 29(A01): 2805-2812.
项彦勇.2014.隧道力学概论[M].北京:科学出版社:35-40.
杨转运.2008.超浅层顶管施工引起路基地层移动数值模拟[J].重庆建筑大学学报, 30(5): 58-62.
喻军,龚晓南.2014.考虑顶管施工过程的地面沉降控制数值分析[J].岩石力学与工程学报, 33(1): 2605-2610.
张帆, 张戈, 徐秀峰, 柳献.2023.钢纤维混凝土管片结构力学特性研究[J].铁道科学与工程学报, 20(9):3463-3475.
张府, 陈有亮, 李林.2019.基于随机介质理论分析盾构隧道开挖引起的地表沉降[J].水资源与水工程学报, 30(3): 237-241.