基于LCSPSO-BTSVM的焊缝表面缺陷检测①
2024-02-26姜怀震
姜怀震, 夏 旭
(1.安徽建筑大学机械与电气工程学院,安徽 合肥 230601;2.工程机械智能制造安徽省重点实验室,安徽 合肥 230601)
0 引 言
焊缝表面缺陷检测不仅对产品质量的界定十分重要,而且对产品的维修保养也很重要[1]。由于机器视觉方法[2-3]对金属表面缺陷检测十分高效、准确率高,因此在3C[4]、半导体及电子[5]、汽车[6]等众多领域中得到广泛的应用。但是针对不同的缺陷定义标准,检测准确率一直在研究。传统的机器视觉检测缺陷的方法主要包括特征提取和缺陷分类两部分,在特征提取上,胡丹等[7]对焊缝缺陷图像预处理后采用HOG提取焊缝激光条纹轮廓图像的特征向量,提取焊缝的轮廓形状,将特征送入支持向量机,证明了该方法的有效性。胡跃明等[8]提出一种基于颜色特征的氧化缺陷检测算法,提取氧化缺陷RGB,HSV颜色特征,输入DAG-SVMS分类器进行分级,实现了铜箔表面氧化缺陷的自动检测。使用一种特征获得信息不够全面,为此Chandrakala M等[9]使用MB-LBP提取图像的纹理特征,使用降维HOG提取边缘特征,通过串行融合,形成完整的图像特征。Kavitha J.C等[10]使用GLCM提取图像的纹理特征,用颜色直方图描述颜色空间中RGB,HSV的颜色特征,分类精度得到提高。上述方法都使用了两种特征信息,相对单特征分类精度得到了提高,但依然没有同时完整充分的利用形状、纹理、颜色三种焊缝缺陷特征信息。此外,传统的机器视觉方法还需要使用分类器分类识别。目前,部分研究者使用深度学习智能算法[11-13]做分类,因为其在大数据分类识别中效果十分优秀,但实际工作应用中,针对小样本分类时SVM与之相比依然在分类效率、复杂度、分类能力和鲁棒性上有一定的优势。Li[14]采用SIFT算法提取特征点,用K-means聚类算法进行聚类,构建每幅图像的BOW(bag of word),最后使用支持向量机对图像进行分类,实现了的预期的分类效果。为了获得更好的分类精度,潘峰等[15]提出了一种基于支持向量机(SVM)与粒子群优化(PSO)相结合的管道腐蚀缺陷的分类方法,采用PSO算法优化SVM参数,提高模型的缺陷分类准确率。但是PSO在寻优时极易陷入局部最优,存在伪随机、后期计算精度低的问题,可能导致分类准确率降低。
针对以上问题,在总结前人经验的基础上设计一种融合几何形状、纹理和颜色三种敏感特征信息的方法,充分利用缺陷信息,并引入莱维飞行策略、Circle混沌映射与单纯形反射操作改进PSO算法,以便取得SVM分类的最优参数,提高焊缝缺陷分类的准确率。
1 焊缝表面缺陷的类型
研究钢板焊缝缺陷分气孔、裂纹和焊瘤三种,如图1所示。
三种类型的焊缝缺陷的特点如表1所示。

表1 焊缝缺陷特点

(a)正常焊缝 (b)焊瘤

2 焊缝缺陷分类算法的改进
2.1 SVM原理
SVM用于二分类,通过计算空间中各样本与超平面的距离,来判断该超平面的选取是否合理,通过对超平面的不断调整,实现最好的分类效果。
最优解的表达式为式(1):
(1)
典型的核函数有四种,由于径向基核函数能降低计算复杂性,效果优秀,故将其作为分类器核函数,公式为:K(x,y)=exp(-‖x-y‖2/σ2),σ>0。
2.2 粒子群算法的改进
PSO于1995年最先提出的启发式算法,通过模拟的群体智能来对目标函数进行优化。假设在一个D维的搜索空间中,第i个粒子位置Xi,飞行速度矢量Vi,个体极值Pi,全局极值Pg,粒子的速度更新公式如所示:
(3)

2.2.1 引入Levy飞行策略的改进
针对PSO算法搜索策略过于单一,陷入局部最优就难以跳出的问题,引入Levy飞行策略,利用其小步长与大步长相结合的跳变方式来扩大搜索范围的方式达到跳出局部最优的目的。改进后的粒子位置更新公式为式(4),(5):
(5)
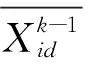
Levy~u=k-ζ
(6)
式(6)中:1<ζ<3为指数系数。Levy分布的数学模型为式(7):
L(s,γ,μ)=
式(7)中:γ、μ均大于0;γ是尺度参数,μ是位置参数;将正态分布的方法应用到Levy分布的函数当中,可以求得其随机步长如公式(8)所示:
(8)
Γ(x)为gamma函数,即Γ(x)=(x-1)!。
2.2.2 引入Circle混沌映射的改进
PSO采用伪随机方式初始化粒子,会出现粒子分布不均,粒子多样性降低,易陷入局部最优无法跳出。针对此问题,采用混沌模型进行映射,改善粒子分布情况,提高粒子个体的多样性。Circle映射均匀性相似且更加稳定,非边缘范围内分布更加均匀,故选择Circle混沌映射初始化粒子。表达式如式(9):
(9)
2.2.3 引入单纯形法的反射操作的改进
针对粒子群算法在搜索后期可能出现计算精度低的问题,采用单纯形法的反射操作计算当前最优反射解,融入到PSO算法中以提高计算精度。
如图2所示,Xg是全局最优位置,Xb为次优位置,Xc为中心点;Xr是反射点;Xe是扩张点;Xt是外收缩点;Xw是内收缩点,Xi为最差点。其计算公式如式(10):
Xr=Xc+α(Xc-Xi)
(10)
式(10)中α=1,它是表示反射程度的参数。
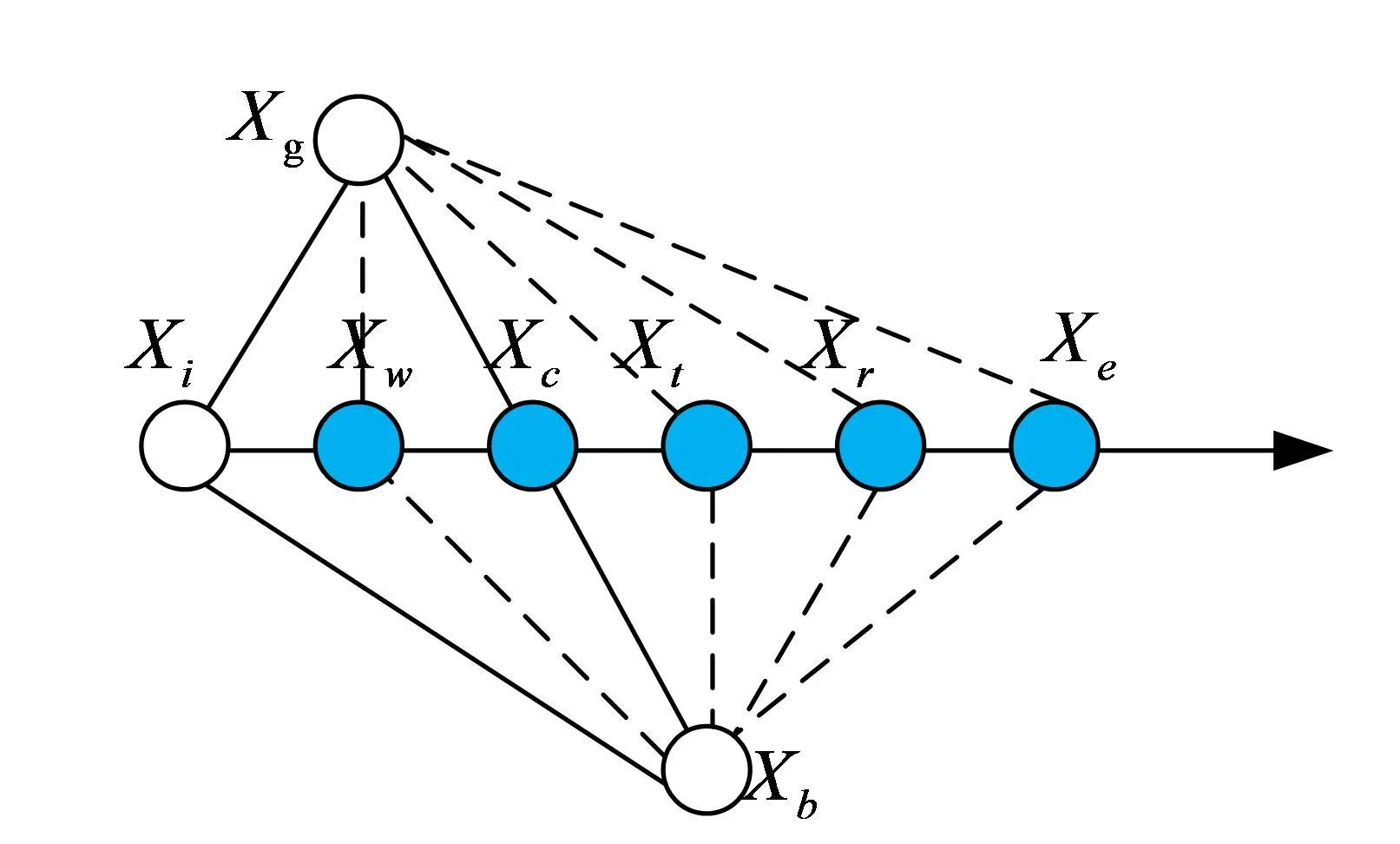
图2 单纯形法运算示意图
LCSPSO算法的具体过程如图3所示.
3 结果与分析
3.1 验证LCSPSO算法的性能
为验证LCSPSO算法的性能,将LevyPSO,PSO算法与改进后的LCSPSO算法作对比,使用四个测试函数测试,设备为win10系统笔记本,内存16 GB,主频频率3.2 GHz,编程试验软件为Matlab 2021b。三种算法设置共同的参数值,w=0.9,c1=1.6,c2=2,粒子种群数量设置为30,粒子的迭代次数设置为500次,实验所选复杂函数2个为单峰函数,2个是多峰值函数,这些函数的具体表达式,实验过程中选中的维数、范围及理论值等相关信息如表3所示,实验结果如表2所示。为了清晰的展示出这三种算法在这4个函数中收敛的特性,绘制他们的收敛曲线如图4所示,在这三种算法中LCSPSO的函数值最低,在f2,f4中,LCSPSO在50代以内就快速下降且从图中明显看出其下降的曲线几乎在横坐标上。这证明了LCSPSO算法的寻找最优解的能力最强。也说明另外两个算法,陷入了局部最优值由f2函数的图像可知,LCSPSO,LevyPSO在最后都接近相同的值,但是LCSPSO的下降速度明显比LevyPSO明显要快。LCSPSO算法和其他几个算法比,其结果最接近理论值,其次是LevyPSO,最后才是PSO。

图3 LCSPSO算法流程图

表2 测试函数
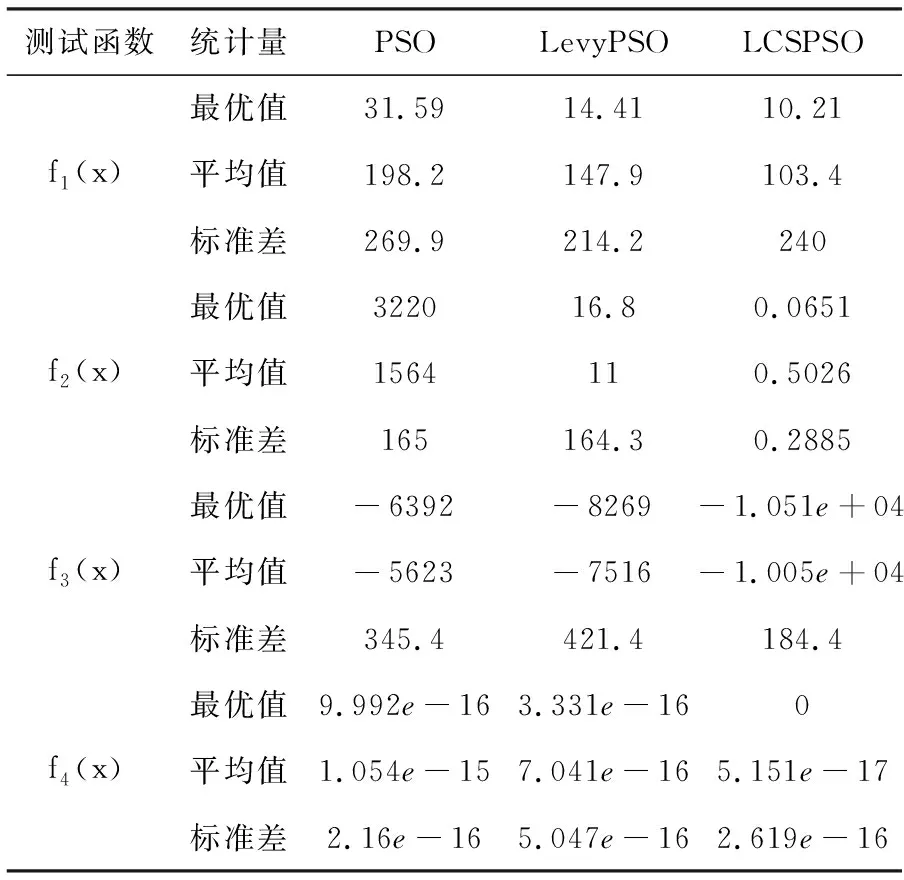
表3 测试函数的实验结果
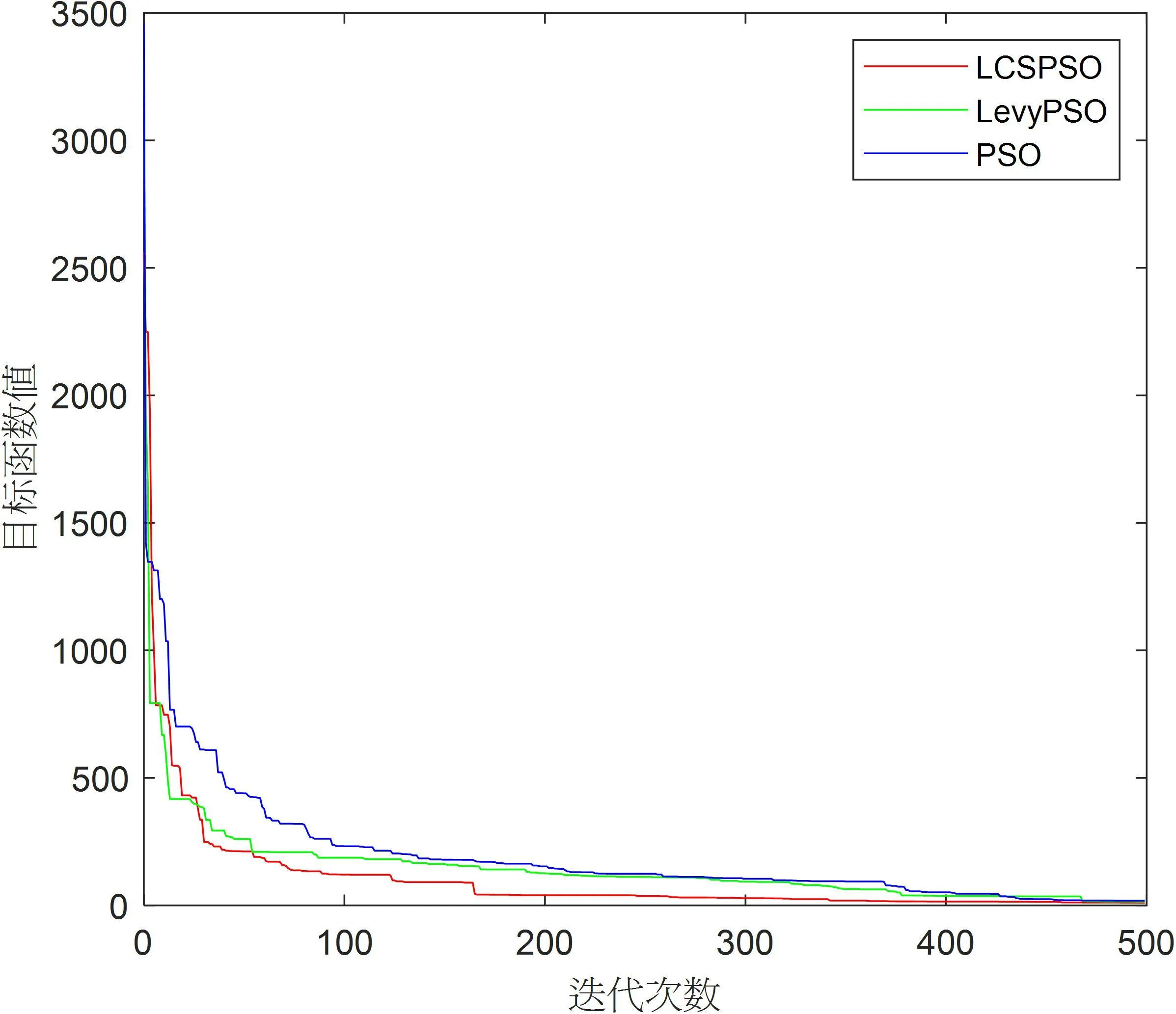
(a)f1迭代收敛曲线 (b)f2迭代收敛曲线

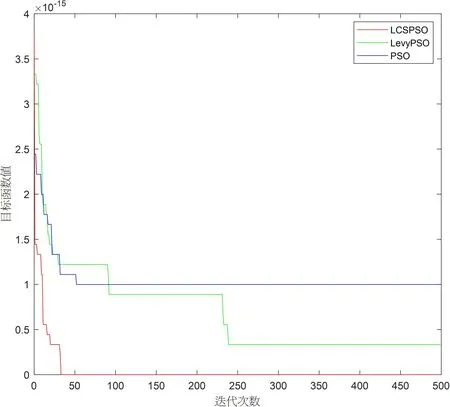
(c)f3迭代收敛曲线 (d)f4迭代收敛曲线
3.2 焊缝缺陷图像分类检测模型
焊缝缺陷图像分类检测模型如图5所示,取钢板表面焊缝缺陷样本数357个,按照7∶3的比例划分训练集和测试集,训练样本数为249个,预测样本为108个。将数据集送到SVM训练。标签1表示正常无缺陷,样本标号从1~62;标签2表示裂纹缺陷样本,标号从63~124、标签3表示气孔缺陷的样本,标号从125~186、缺陷4表示焊瘤缺陷的样本,标号从187~249。试验使用的SVM是libsvm3.31,初始的参数c1,c2都设置为2,种群最大数量设为10,C,σ的范围设置为0.1~100。通过5折交叉验证以获得最优的C,σ,分类的准确率设为适应度函数。

图5 焊缝缺陷图像分类检测模型
3.3 焊缝缺陷分类检测不同算法对比分析
LCSPSO,PSO,LevyPSO优化BTSVM对焊缝缺陷图像分类检测,实验结果如图6和表4所示,LCSPSO-BTSVM的适应度最大97.189%,C=16.8,σ=0.8。平均准确率适应度曲线变化范围较大,说明该算法搜索范围较大,准确率为99.07%,图中的混淆矩阵反应真实值与预测值的准确度,在图中标签1、标签2、标签4正确率100%,标签3,正确率只有96.3%。LevyPSO-BTSVM的C=11.9060,σ=0.1593,LevyPSO-SVM的适应度为94.779%,PSO-BTSVM的适应度为91.968%,LevyPSO-BTSVM分类准确率为94.45%,PSO-BTSVM分类准确率为87.04%,都低于LCSPSO-BTSVM的99.07%。以上试验表明LCSPSO-BTSVM的分类准确率明显的提高。
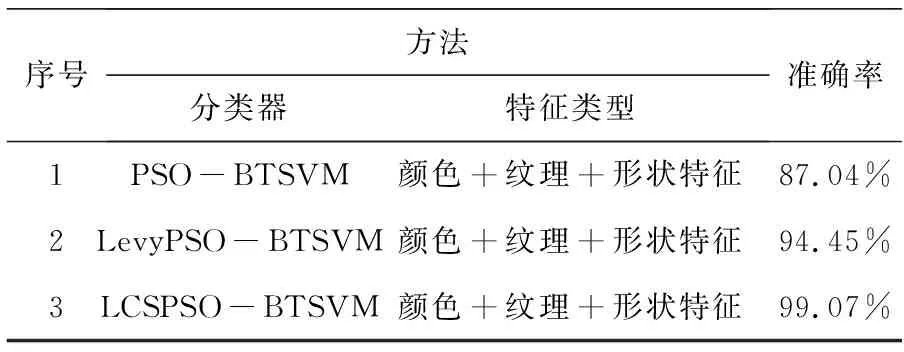
表4 不同算法对比实验结果统计表

图6 实验对比图
4 结 论
1)针对粒子群算法容易陷入局部最优、初始种群多样性低、后期计算精度低问题,引入莱维飞行策略、Circle混沌映射、单纯形反射操作来优化PSO算法,使用4个经典复杂函数验证并与其他算法作对比实验,结果证明LCSPSO算法优于PSO,LevyPSO。
2)通过设计的合理BTSVM分类器利用LCSPSO对焊缝表面缺陷进行分类检测并与PSO-BTSVM,LevyPSO-BTSVM作对比试验,结果表明LCSPSO-BTSVM的检测准确率达到99.07%,优于其他算法。
