基于扩展移相的ISOP-DAB变换器混合优化控制方法

陶海军, 王宏祎, 杨乃通

(1.河南理工大学电气工程与自动化学院, 河南 焦作 454003; 2.河南省智能装备直驱技术与控制国际联合实验室, 河南 焦作 454003)

1 引言

双有源电桥(Dual Active Bridge, DAB)DC-DC变换器具备能量双向传输、能量密度高、宽电压转换范围及功率器件零电压开关等优势[1,2]受到广泛关注,在电力电子变压器、电动汽车、智能电网和能量储存系统等[3-6]多种现代电力设备中得到广泛推广。随着操作的电压水平和功率水平的不断提高,在高压直流电网中,DAB变换器被用作级联变换器的基本组件,通过串并联组合可形成输入串联输出并联(Input Series-Output Parallel, ISOP)DAB变换器结构[7],不仅打破现有开关器件的电压应力限制[8],同时具备可扩展性和冗余操作的特点[9],具备模块化设计,单模块功率水平降低使系统更容易设计,电压应力降低易于选择功率器件,使其在电力电子变压器中成为重要的DC-DC级拓扑之一[10]。

ISOP-DAB变换器在实现拓宽功率等级的目标同时,具备单一模块的各项基本特性。在变换器的控制方式中,最常用且最简单的是移相控制[11,12],可以分为单移相(Single Phase Shift, SPS)控制、双重移相(Dual Phase Shift, DPS)控制、扩展移相(Extend Phase Shift, EPS)控制和三重移相(Triple Phase Shift, TPS)控制。文献[13]是根据DPS控制原理提出来的关于电流应力控制的系统优化方法。该方法在电流应力优化方面产生一定效果,但在轻载条件下并未达到理想优化效果。文献[14]以TPS控制为基础,实现电流应力在三维空间层面最优的相位矢量控制,其电流应力优化方面效果最好,但存在系统的建模及分析较为复杂、可移植性差等问题[15]。EPS控制是在SPS控制的基础上,仅在变换器一侧全桥增加移相角。相较于DPS控制提高了灵活性且扩展了功率选择范围[16],同时控制复杂度方面相较于TPS控制得到优化。

在面对极端情况时ISOP-DAB变换器保持稳定运行或快速恢复稳定状态,同时针对ISOP结构保证模块间的传输功率动态均衡[17],都是衡量控制策略的重要参考依据。在控制组成模块之间的功率平衡时,可通过控制输入电压共享(Input-Voltage Sharing, IVS)或输出电流共享(Output-Current Sharing, OCS),间接控制模组间功率平衡,但OCS控制不稳定而普遍使用IVS控制[18]。共同占空比控制在理想情况下所有模块使用同一个输出电压闭环回路,对各模块施加相同的占空比信号,从而实现各模块间的功率平衡[19],但这种控制结构简单,系统的稳态和动态性能较差且实际电路中元件之间存在误差,模块间不对称导致其传输功率也不再相同[20]。针对这一问题,文献[21]提出了一种三环控制,在共同占空比的输出闭环基础上,增加输出电流环提高动态性能,配合输入电压环形成三环控制使系统在波动时完成校正,但其校正时间较长。文献[22]提出了模型预测控制,以控制传输功率均衡为目标,并提升了系统在面对极端情况下的反应速度,但在电流应力优化方面没有深入研究。针对ISOP-DAB变换器,上述文献均未能同时实现电流应力优化、快速动态响应和保持功率均分的控制目标。

本文以扩展移相以电流应力优化与虚拟电压均衡为重点,针对ISOP-DAB变换器提出了混合优化控制方法(Hybrid Optimal Control with Extended Phase Shift control,HOC-EPS)。首先分析DAB变换器的三种工作状态,根据拉格朗日优化原理,推导出电流应力优化公式及其移相量组合D1和D2对应的计算公式。然后借鉴直接功率控制的思想由DAB变换器的传输功率实时估算以提高动态响应速度,维持模块间的功率均衡。最后,以基于单移相的虚拟功率控制(Virtual Power Control with Single Phase Shift control, VPC-SPS)[23]和传统的扩展移相优化控制(Traditional Optimization Control with Extended Phase Shift, TOC-EPS)算法[12]为参考,对所提控制策略进行对比实验验证。

2 扩展移相控制

图1展示了由N个单模块DAB变换器组成的ISOP-DAB变换器拓扑及其等效电路结构。Uin和Uo分别为ISOP系统输入、输出端的总电压,rs为变换器电源的等效内阻,R为系统等效负载。第i(i=1,2,…,N)个DAB变换器由两个H桥和一个变压比为n∶1的高频变压器组成,k为系统电压比,k=Uin/(nUo),L为第i个变换器的变压器漏电感和系统辅助电感之和,Uab和Ucd分别为两侧全桥的输出和输入电压。

图1 ISOP-DAB变换器拓扑结构Fig.1 ISOP-DAB converter topology

针对第i个DAB变换器单独分析,在EPS控制下,开关管的栅极信号波形和高频变压器两端电压Uab和Ucd的波形如图2所示。

图2 EPS控制下DAB变换器单元波形Fig.2 DAB converter unit waveform under EPS control

由图2可知EPS控制有两个控制自由度D1和D2。移相角D1为产生三电平电压侧电桥的对角开关管的相移量,移相角D2为变压器两端电压Uab和Ucd高电平电压之间的移相角差,Ts为开关周期的一半。

本文以电压比k>1为例,根据移相角D1和D2之间关系将DAB变换器分为三种模态:0≤D2≤D1/2、D1/2≤D2≤1-D1/2和1-D1/2≤D2≤1,移相角D1和D2之间关系和电压电流波形如图3所示。

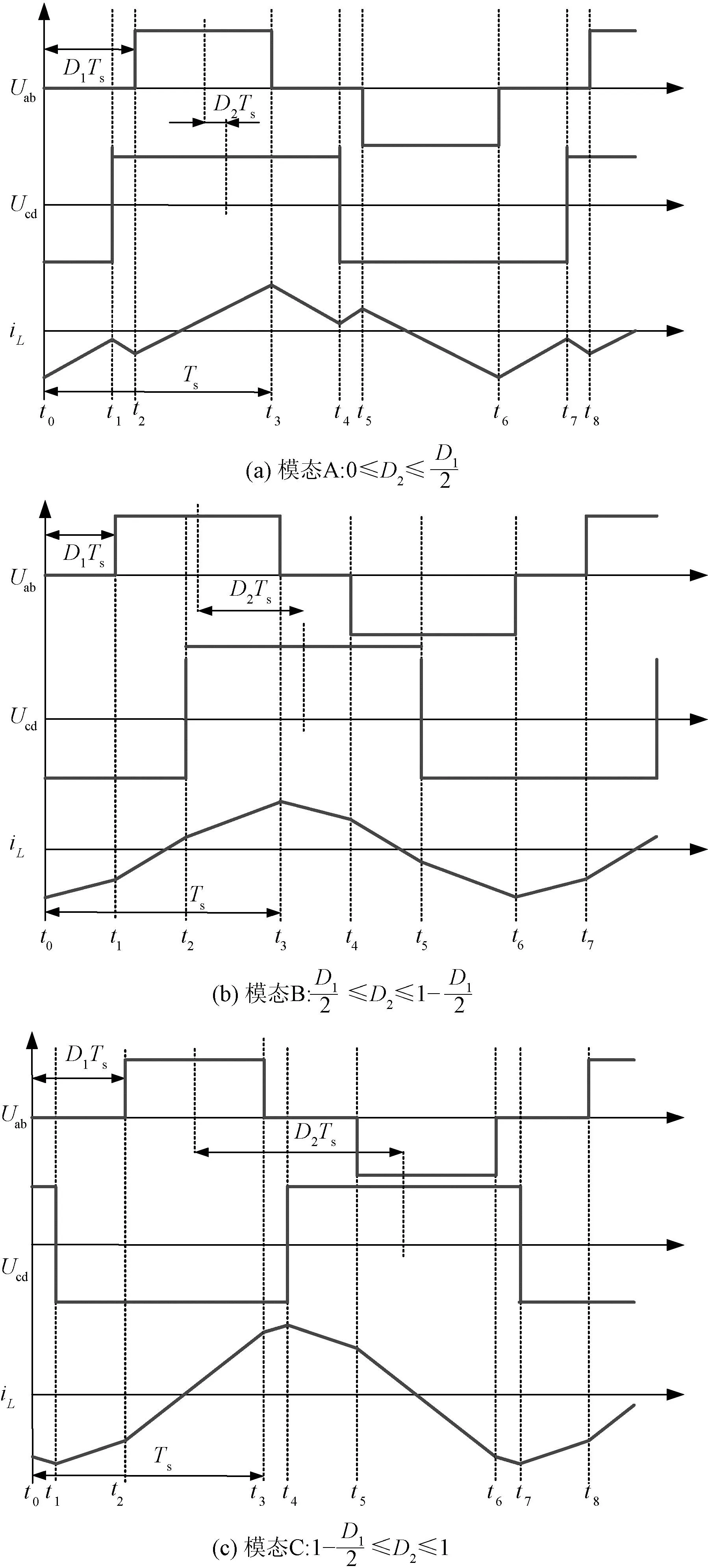
图3 DAB变换器在EPS控制下的电压电流波形图Fig.3 Voltage and current waveform diagram of DAB converter under EPS control

EPS调制下DAB变换器的平均传输功率和最大电流应力公式为:

(1)

结合式(1)在扩展移相控制下,DAB变换器的最大传输功率和最大平均输入电流分别表示为:

(2)

式中,f为系统开关频率。

分析图3并结合式(1)和式(2),则DAB变换器的平均传输功率和最大电流应力的单位值分别为:

(3)

3 混合优化控制方法

现有文献关于动态响应和电流应力两方面优化的研究主要有两种[12,23]:

(1)基于单移相的虚拟功率控制。移相角D通过虚拟功率优化生成,控制算法的控制框图如图4所示。

图4 基于单移相的虚拟功率控制框图Fig.4 Virtual power control block diagram based on single phase shift

(2)TOC-EPS策略。输出电压与额定电压的差值经过PI控制器的计算得到外移相角D2,再通过采样信息和外移相角D2结合求出内移相角D1。控制算法的控制框图如图5所示。

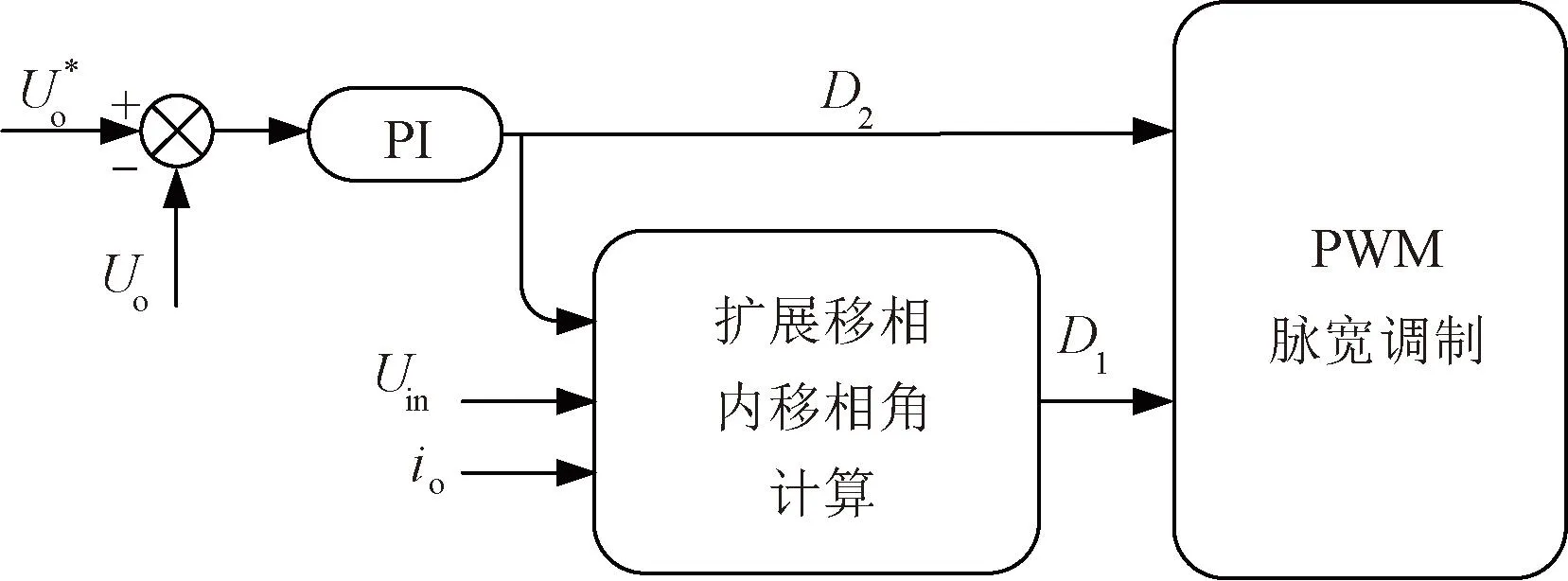
图5 传统的扩展相移优化控制框图Fig.5 Traditional extended phase shift optimization control block diagram

上述两类控制策略都只能优化一个方面。在第一类控制策略中,通过虚拟功率补偿生成移相角D,加快变换器的动态响应速度,但单移相调制使电流应力较大。第二类控制策略中,简单地通过PI控制器计算外相移量D2,再与系统输入电压和负载电流结合计算出内相移量D1,虽然扩展移相调制的使用在一定程度上降低了电流应力,但降低了变换器的动态响应。为了同时实现ISOP-DAB变换器在电流应力、动态响应及功率均分等多方面的优化提高系统的传输效率,结合扩展移相调制本文提出混合优化控制。

系统的平均传输功率Ptr在数值上与输出功率Po近似,为了控制方便一般直接采用输出功率标幺值参与计算,但在实际电路中,变换器全桥中的开关管存在管压降和死区时间等现象,会产生电路损耗或相位漂移等不利因素满足式(4):

Ptr=ηPo

(4)

式中,η为变换器传输效率。

(5)

同时,变换器的输出电流参考值可表示为:

(6)

将式(6)代入式(5)中,推导得:

(7)

与式(2)联立则虚拟功率的标幺值可以表示为:

(8)

式中,Uini为第i个模式输入电压。

式(8)中虚拟电压Uv由系统的输出电压值与参考电压的差值计算得到,实现系统内功率动态平衡,进而加快动态响应速度,同时优化电流应力,提高系统效率。使用系统总输入电压的均值Uin/N,并且通过PI控制器的补偿机制将公式中的常数省略,比如开关频率f、辅助电感L和变换器的变比n。则式(8)可进一步化简为:

(9)

拉格朗日乘数法(Lagrange Multipler Method, LMM)是一种寻找变量受一个或多个约束条件所限制的多元函数的极值方法。将LMM应用到DAB变换器的电流应力优化中,定义拉格朗日函数为:

ILMM=im+λ(Ptr-Pv)

(10)

式中,ILMM为拉格朗日函数;λ为拉格朗日乘子;Pv为计算得出的虚拟传输功率。

(11)

式中,k为电压转换比。

其次,将式(10)中的电流应力和传输功率分别用式(3)中的标幺值代替,将拉格朗日函数分别对移相角和λ求导,计算优化后的移相组合。

不同操作模态经过LMM电流应力优化得到的最佳移相组合见表1。

表1 LMM优化移相组合Tab.1 LMM optimized phase-shifting combinations

表1中电压转换比k由采样的数据直接计算代入。通过表1的优化移相量组合D1和D2,求解相对应的最优电流应力值,联立式(3)得到电流应力最优解为:

(12)

式中,p为系统此刻瞬时功率。

电流应力数值大小对变换器多方面造成影响,较小的电流应力可以保证变压器电感工作在正常磁化曲线范围;同时,变换器电流应力的降低也直接关系了变换器的导通损耗的减少,提高了变换器的传输效率。DAB变换器电流应力的大小与经过变压器的电感电流的绝对平均值相关,而系统的导通损耗与开关管电流(也是电感电流)的数值有关。因此降低电流应力,也就降低了变换器中开关管的导通损耗。

4 模块平衡分析

混合优化控制方法中的优化移相组合是通过虚拟功率补偿拉格朗日优化计算得到,PI控制器用于补偿计算模型和物理系统之间的差异,不影响模块间的平衡问题。对于输入串联输出并联结构DAB变换器,输入侧电流和输出侧电压分别相等,模块平衡主要取决于多模块间输入电压和输出电流的平衡,则式(4)可进一步扩展为:

Uin1∶Uin2∶…∶UinN=η1Io1∶η2Io2∶…∶ηNIoN

(13)

由式(13)得ISOP-DAB变换器的模块间输入电压平衡时,变换器之间输出电流值也相等,输入电压平衡和输出电流平衡是等效的,因此在功率平衡控制中,只需保证输入电压平衡即可。在ISOP-DAB达到稳态运行时,结合功率计算公式可知其输入功率数值比和输入电压的数值比相同,可表示为:

Pin1∶Pin2∶…∶PinN=Uin1∶Uin2∶…∶UinN

(14)

在稳态状态下,输入电压恒定导致流过分压电容的电流ICin1=0,当某一模块发生扰动时,例如模块DAB1的输入电压Uin1由于扰动降低,由式(9)知虚拟功率Pv增大,经过LMM优化移相量D1减小移相量D2趋近0.5,则输入电流Iin1增大,导致DAB1的分压电容电流ICin1<0,使得Uin1继续降低形成正反馈,同时在ISOP-DAB系统输入电压Uin为固定值时,模块1的输入电压Uin1的降低导致其余模块输入电压值升高,如模块DAB2的输入电压Uin2升高,经过功率计算及表1优化后移相量D1增大移相量D2降低,则输入电流Iin2降低,Uin2继续升高从而导致系统失衡。

为避免系统控制电路发生正反馈,在模块间输入电压波动时,应控制模块虚拟功率变化与之保持一致,即Uini升高时通过控制使Pv增大,经过LMM优化后移相量D2趋近0.5控制Uini恢复稳定。在计算虚拟标幺值时使用系统总输入电压的均值Uin/N,因为当系统中一个模块发生异常导致输入电压波动时,则系统中其他模块必然发生与之相反的波动,因此系统输入电压的均值在数值上基本保持不变,再通过PI控制器动态调节Uv使虚拟功率变化与输入电压保持一致,从而达到了模块间输入电压的动态平衡,进而实现模块间功率平衡。

在开环系统中,高频变压器的不匹配将导致模块间无法达到输入电压平衡,如在控制DAB模块的移相组合相同的情况下,由式(2)可知系统高频电感小的模块其传输功率值较高,表现为模块的输入电流值大从而使分压电容电流ICin降低,相应的模块输入电压也随之降低,由此可知,模块间高频电感值大的输入电压高,电感值小的输入电压低。在实际应用中,每个模块的电感参数之间的差异通常在10%以内,在HOC-EPS控制下通过PI控制器对虚拟电压的补偿,消除了系统电感参数不一致导致的模块间传输功率的误差,虚拟功率估算计算出的每个DAB模块的虚拟功率成为模块传输功率Ptr的约束条件,生成三个DAB模块的优化移相组合,因此模块高频电感的不匹配并不会影响到均压控制。

通常在EPS控制中,理想的开关管脉冲信号是通过比较参考电压和三角载波生成,但实际中三角载波是离散的,因此会产生脉宽误差影响每个模块的均压效果,且随着开关频率的增加,脉宽误差相应地也会增加。由文献[24]可知系统频率在50 Hz内时PWM分辨率为100%,则脉宽误差不会影响到系统的均压性能。

混合优化控制方法通过下列过程实现调制:首先,对ISOP-DAB变换器的基本参数进行采样。然后,由采样值计算电压转换比k再通过式(9)计算系统Pv值。其次,通过式(11)由LMM优化得到使电流应力最优的相移量组合D1和D2。最后,用D1和D2控制扩展移相调制进一步生成特定的开关管驱动信号,图6为其控制框图。

图6 基于扩展移相的混合优化控制框图Fig.6 Mixed optimization control block diagram based on extended phase shift

5 实验结果及分析

为验证对混合优化控制策略理论分析的正确性和有效性,搭建三模块ISOP-DAB实验平台对上述控制策略进行验证,表2为变换器具体电路参数。

表2 三单元ISOP-DAB变换器具体电路参数Tab.2 Specific circuit parameters of three-unit ISOP-DAB converter

实验验证可分为三部分:功率平衡实验、动态特性实验与电流应力及效率实验。为了突出混合优化控制策略的有效性,将混合优化控制方法与基于单移相的虚拟功率控制策略和传统的扩展移相优化控制作对比实验。

5.1 功率平衡实验

控制ISOP-DAB变换器的输入电压Uin为390 V,输出电压Uo为50 V,负载由10 Ω加重到5 Ω时,单模块DAB变换器输出功率由83.3 W升高至166.6 W,系统总输出功率500 W,图7(a)为三个模块间输入电压波形图。图7(b)输入电压由390 V向450 V突变的暂态过程,即单模块由130 V向150 V突变的过程,单模块传输功率由220 W降低至193.3 W,系统总传输功率降低至590 W。图7(c)为系统在输入电压Uin为390 V和负载5 Ω下稳态时ISOP-DAB变换器三个模块间的电感电流的波形图。

图7 ISOP-DAB变换器功率平衡波形图Fig.7 ISOP-DAB converter power balance waveform

分析图7并结合式(14)可知,三个模块的输入电压在系统突变的暂态过程中实现了很好的均压效果,从而完成功率平衡的目标。同时三个模块间流经变压器中的电感电流iL1、iL2和iL3分别为7.4 A、7.48 A和7.45 A,混合优化控制很好地实现了变压器电感之间的电流共享。

5.2 动态特性实验

设置ISOP-DAB变换器输入电压Uin=390 V(即单个模块输入电压为130 V),输出电压Uo=50 V。通过控制负载突变验证ISOP-DAB变换器的动态特性,图8为输出电压和负载电流在负载发生突变输出功率由250 W升高到500 W时(即单个模块输出功率由83.3 W升高至166.6 W)变化的波形图。

图8 负载突变时电压电流对比实验波形图Fig.8 Comparison experimental waveform plot of voltage and current during sudden load change

通过分析可知,在负载突变时,传统的扩展移相优化控制相较于混合优化控制方法动态性能较差,在负载突变时输出电压恢复稳定的响应时间大约为228 ms,同时输出电压偏离参考电压值较大,达4.1 V。而在混合优化控制方法下,系统的动态性能良好,其输出电压基本保持稳定。

设置ISOP-DAB变换器输出电压Uo=50 V,负载电阻R=5 Ω。通过控制输入电压突变验证系统的动态特性,令系统输入电压由390 V升至450 V,此时系统传输功率由660 W降低至590 W(即单模块传输功率由220 W降低至193.3 W),图9为输入电压和负载电压的变化波形图。

图9 输入电压扰动时电压对比实验波形图Fig.9 Voltage comparison experimental waveform plot when the input voltage suddenly changes

通过分析可知,在输入电压扰动时,传统的扩展移相优化控制效果相较于混合优化控制较差。传统的扩展移相优化控制输出电压恢复稳定的响应时间约为138 ms,输出电压数值偏离参考电压值约为4.3 V。而混合优化功率控制方法在输入电压突变时,动态响应迅速使变换器的输出电压基本保持稳定不变。

5.3 电流应力优化实验

设置ISOP-DAB变换器输入电压Uin=390 V(即单个模块输入电压为130 V),输出电压Uo=50 V,系统输出功率250 W,即单模块输出功率83.3 W。图10为变换器其变压器两侧的电压波形及电感电流波形。

图10 3种控制方法下的电压电流实验波形图Fig.10 Voltage and current experimental waveform under three control methods

通过分析图10可知,在ISOP-DAB变换器的输入电压较大即k值较大时(k=Uin/(nUo)=2.6),表现为单个模块的DAB变换器的输入侧电压与负载端电压差值较大。VPC-SPS控制产生的电压电流波形下,其策略控制使得电感电流应力大约为10.2 A。TOC-EPS产生的电压电流波形,相较于上一种控制策略减小了变换器的电流应力在优化下数值约为7.1 A。虽然优化了电流应力,但传统的扩展移相控制并未达到最理想效果,其计算产生的移相量组合不是最优组合,因此得到的电流应力最优解还能更进一步优化。HOC-EPS控制在电流应力优化方面达到最优,具有最优化的移相量组合,因此其电流应力优化效果也达到最佳约为5.8 A。

ISOP-DAB变换器的电流应力和传输效率是变换器高效运行重要的性能指标。为了直观体现不同控制方式之间优化效果的差异,图11绘制了ISOP-DAB变换器在输入电压Uin由50 V至150 V阶梯之间的电流应力和效率曲线图。通过分析图11可知,在保持输出电压不变输入电压的增大下即本质上令电压转换比增大,在文中3种控制策略下,其电流应力变化都与电压转换比变化保持一致性,相应地导致传输效率的降低。其中电流应力优化效果最差的是基于单移相的虚拟功率控制策略,其控制下的电流应力数值相较于其他控制方式递增幅度最大,最大值为12.9 A,相应地导致变换器传递效率最低为77.1%。与之相比较,传统的扩展移相优化控制方法优化效果得到基本改善,降低了电流应力数值从而提高效率,随着电压转换比的增大这一现象更加明显,在电压转换比达到最大时电流应力为7.96 A,效率为83.2%。然而,在本文所提的混合优化控制方法下,ISOP-DAB变换器的优化效果达到最优,当电压转换比达到最大时其最大的电流应力仅为6.49 A,同时在其控制下的效率进一步提高达86.3%。

图11 变换器电流应力和效率曲线图Fig.11 Converter current stress and efficiency

6 结论

本文在扩展移相的基础上针对ISOP-DAB变换器的电流应力、动态性能及功率均分等方面提出了一种混合优化控制方法。分析了ISOP-DAB变换器在扩展移相中三种移相量状态下的电压电流波形图并进行LMM优化得到在全范围内的电流应力优化函数,借鉴直接功率控制思想计算虚拟电压分量实现对传输功率的实时估算以提高变换器的动态响应速度,同时动态调节变换器模块间功率均衡。通过理论分析,再将文中提出的混合优化控制方法与基于单移相的虚拟功率控制策略和传统的扩展相移优化控制作对比实验,结果表明:

(1)在混合优化控制下,变换器的输出电压基本保持稳定,其动态性能达到最优。

(2)相比于传统的电流应力优化算法,混合优化控制策略降低变换器电流应力的效果更好。

(3)混合优化控制方法具有较强的动态调节能力,能够快速调节模块间功率均分。