基于机器学习模型的北海市银海区小流域地表水中铵氮污染预测

2024-02-24王令占谢国刚张宗言

安全与环境工程 2024年1期

涂兵,杨博,王令占,李响,谢国刚,马筱,张宗言

(中国地质调查局武汉地质调查中心(中南地质科技创新中心),湖北武汉 430205)

近年来,机器学习方法因其能够很好地描述不同变量之间的复杂关系而被广泛应用于预测各种水体中污染物浓度的空间分布[5-9]。多元线性回归模型长期以来一直被用于水体污染物浓度预测,虽然多元线性回归模型结构简单,但与复杂的模型相比,其性能仍具有竞争力[6]。而针对数据量较小的数据集,支持向量机因其稀疏表示而具有出色的泛化能力,因此也被广泛用于污染物浓度预测[10-11]。随机森林是一种基于树的集成算法,能够处理输入变量之间的相互依赖和非线性关系,前人的相关工作已经证明了该方法的可靠性[12-15]。

1 材料与方法

1.1 研究区概况

冯家江流域、三合口江流域和福成河流域位于广西壮族自治区北海市区南部沿海(图1)。研究区位于北回归线以南,属亚热带季风型海洋性气候,阳光充足、雨水丰沛,多年平均气温为22.6 ℃,多年平均降雨量约为1 751 mm,降雨主要集中在每年的5—10月份,降雨量占全年的80%以上,年均蒸发量约为1 166 mm。河流容易受到潮汐作用影响而不断变化。研究区位于南康盆地,南康盆地基底为志留系、泥盆系砂岩、泥岩,盆地上覆盖第四系、新近系互层状的松散砾石、砂和黏土,松散层厚度自北向南呈增厚之势,最厚达200 m以上。其中,第四系松散沉积物广泛分布于冯家江、三合口江和福成河两岸,岩性主要为全新世灰、灰黄色砂砾、含砾砂、粉砂、砂质黏土、黏土等,含腐殖质,具下粗上细的二元结构。

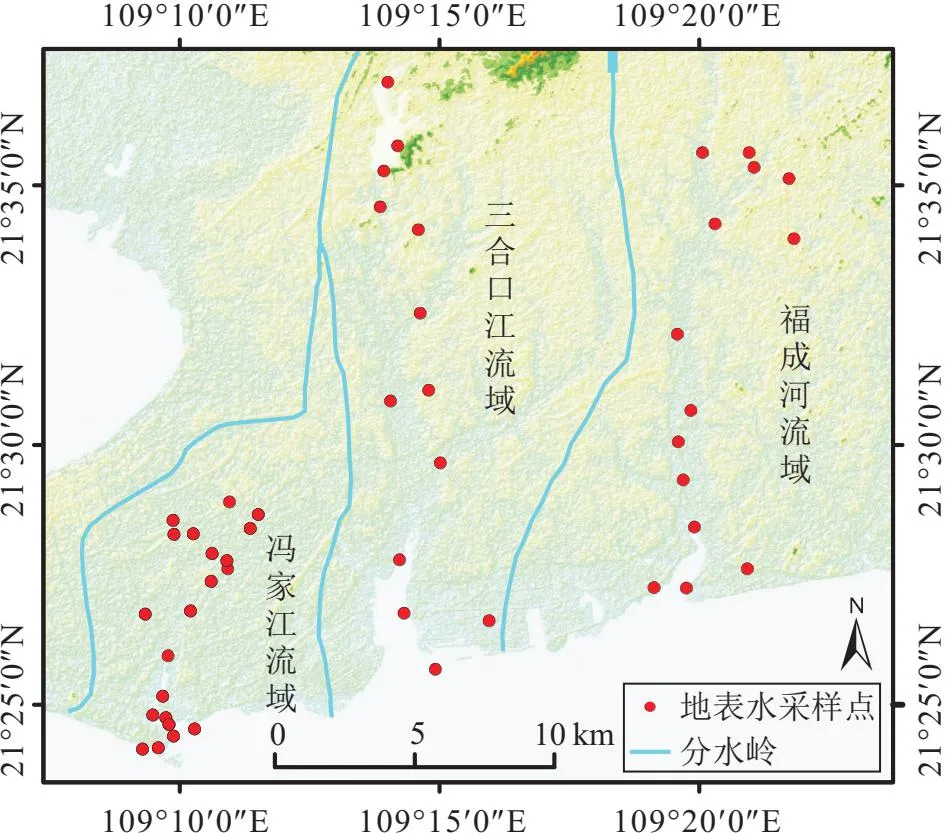
图1 研究区地理位置和地表水采样点分布Fig.1 Geographic location of the study area and distri-bution of surface water sampling sites

1.2 样品采集与测试分析方法

2021年7月至8月,分别对冯家江流域、三合口江流域和福成河流域地表水进行了采样。采样主要遵循以下原则:①地表水取样点尽量选择代表性的采样点;②采样点涵盖研究区不同地理特征和水文条件;③在河流上游、下游以及河流入海口等位置选取采样点,在水质发生变化处适当加密采样点。水样采集点利用GPS精确定位,其中冯家江流域地表水样40个,三合口江流域地表水样13个,福成河流域地表水样14个,具体采样点位分布见图1。

无机物采样瓶采用500 mL高密度聚乙烯瓶,取样前用待取水样润洗3次。地表水样采用1 L采样器在水面下约0.5 m处采集;采集地下水样时,先用低流速潜水泵抽取3～15 min,待水温、pH值、溶解氧(DO)、氧化还原电位(ORP)等现场测试指标达到稳定后再采集地下水样品。所有无机物测试样品经0.45 μm水系滤膜过滤后分别装入3个500 mL聚乙烯瓶中,不留顶空。其中,1瓶水样加入适量浓H2SO4调节pH值至小于2,用于主要阳离子测试,其余2瓶水样用于主要阴离子和其他指标测试。所有水样均置于4 ℃冰箱并避光保存,并于取样后一周内完成实验室测试分析。

1.3 机器学习模型

1.3.1 多元线性回归模型

多元线性回归模型是一种用于建模和预测因变量(响应变量)与多个自变量(特征)之间关系的统计方法。它假设目标变量与自变量之间存在线性关系,并且通过寻找最佳拟合直线来建立这种关系。多元线性回归模型的数学表达式如下:

y=β0+β1x1+…+βnxn+ε

(1)

式中:y为目标变量(预测值);x1、x2、…、xn为自变量(输入变量);β1、β2、…、βn为模型的参数,表示每个自变量对应的权重(斜率);ε为误差项,表示模型无法完全解释的随机误差。

多元线性回归模型的目标是找到一组最优的参数β1、β2、…、βn,使得预测值y与实际值(观测值)尽可能接近。

1.3.2 支持向量机模型

支持向量机模型的目标是找到一个超平面f(x),使得样本数据点尽可能地靠近这个超平面[20]。这一方法适用于解决连续变量的预测问题。支持向量机的数学表达式如下:

(2)

式中:f(x)为预测函数,用于预测目标变量y的值;β0为回归模型的截距项;αi为拉格朗日乘数,用于表示每个样本点的权重;K(x,xi)为核函数,用于将样本数据x映射到高维特征空间,并计算预测函数f(x)的值。在本研究中,核函数选用线性核函数。

1.3.3 随机森林模型

随机森林模型是一种集成学习算法,它采用集成学习的思想,将多个决策回归树组合成一个强学习器,通过集成多个决策回归树的预测结果,可以获得更准确和稳健的回归结果[20-22]。决策回归树是一种树状结构的回归模型。首先,它通过对特征空间进行不断划分,将数据分为不同的区域,并在每个区域内拟合一个常量值作为该区域内所有数据点的预测值。单独的决策回归树容易过拟合,但通过集成多棵决策树,可以降低过拟合的风险。其次,在构建每棵决策树时,随机森林模型会对训练数据进行随机采样(有放回采样),这意味着每棵决策树的训练数据都是不同的。这样可以使得每棵决策树看到不同的样本数据,增加了模型的多样性[20]。最后,随机森林模型将各个决策树的预测结果取平均作为最终预测值。通过平均的方式,可以降低个别决策树的误差对最终回归结果的影响,提高了模型的稳健性。随机森林模型的数学表达主要涉及多个决策树的组合和回归结果的计算。对于含N棵决策树的随机森林模型,每棵决策树i的回归模型可以表示为

(3)

式中:fi(x)为第i棵决策树的回归输出,表示预测值;Mi为决策树i的叶节点数目;cij为决策树i第j个叶节点的输出值;Rij为决策树i第j个叶节点对应的区域,表示样本x被划分到该叶节点的条件;I(x∈Rij)是一个指示函数,当x属于Rij时,取值为1,否则为0。

随机森林模型的最终输出是所有决策树回归预测结果的平均值,其表达式为

(4)

1.4 模型训练

图2 模型训练与预测流程图Fig.2 Flowchart of model training and prediction

2 结果与讨论

2.1 模型性能评估

表2列出了北海市银海区小流域地表水样分析数据集(训练集和测试集)的描述性统计结果。通过对比训练集和测试集上的观察值和预测值,可以直观地看出3种预测模型的性能(图3)。

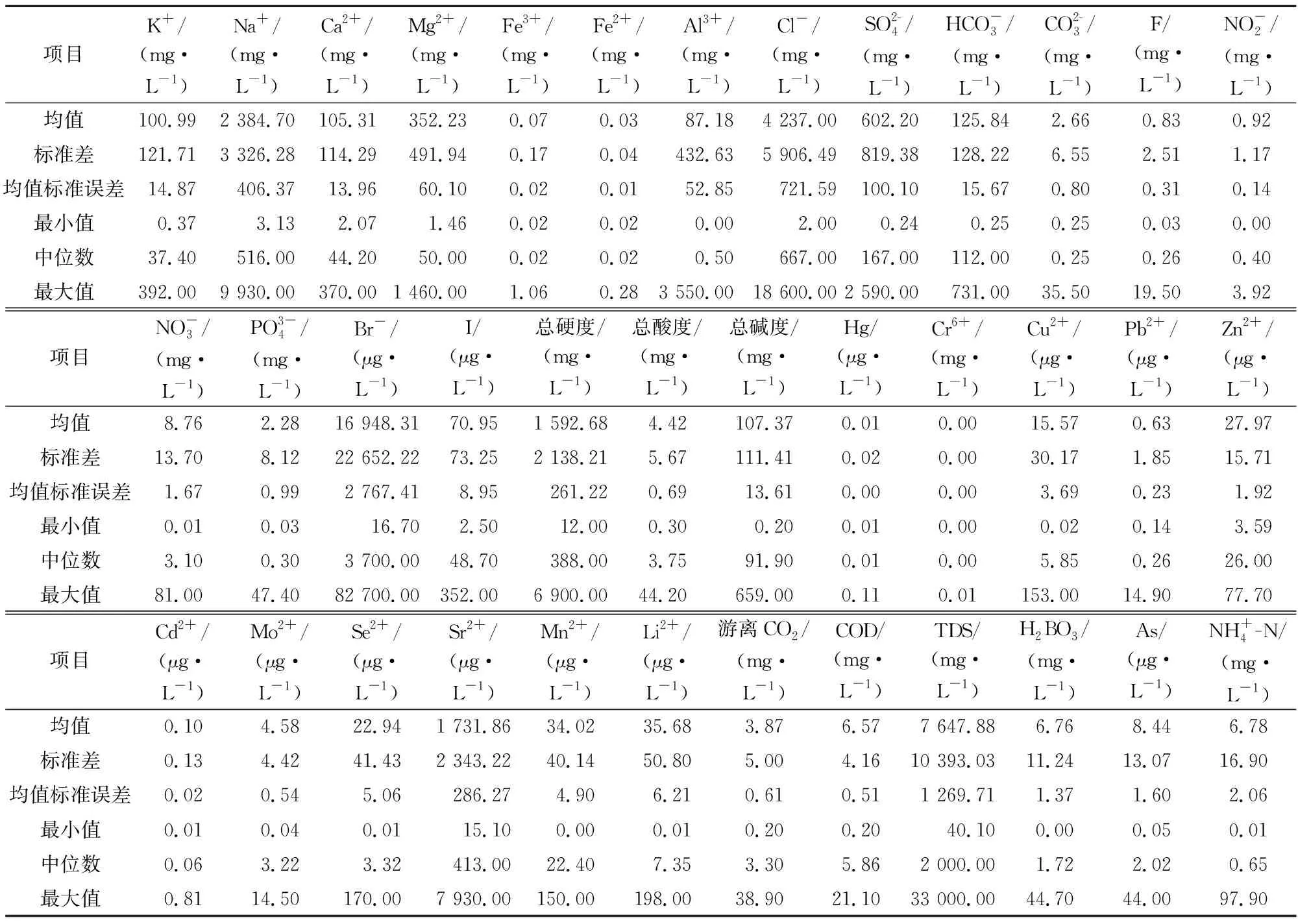
表2 北海市银海区小流域地表水样分析数据描述统计结果

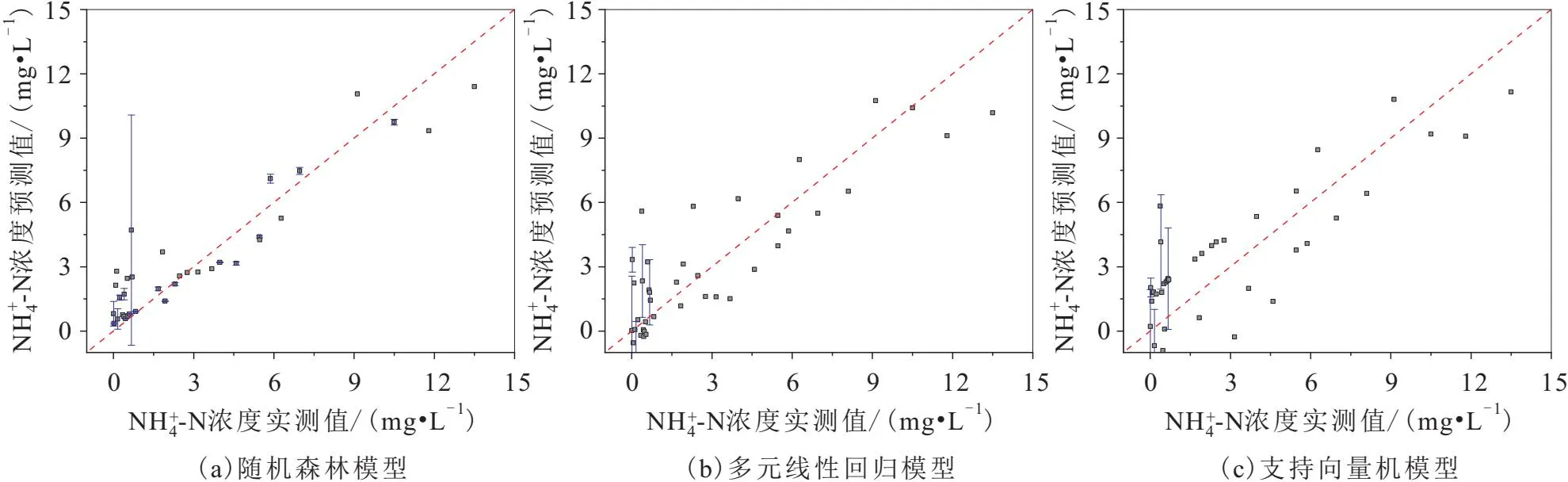
图3 随机森林模型、多元线性回归以及支持向量机模型在测试集上预测地表水中N-N浓度与实际浓度的对比Fig.3 N-N concentrations predicted by random forest model,multiple linear regression model and support vector machine model based on the test set in surface water versus actual concentrations

由图3可以看出:随机森林模型的预测值最为准确,其在y=x线上的分布最为集中,而多元线性回归模型与支持向量机模型的预测效果较为接近。

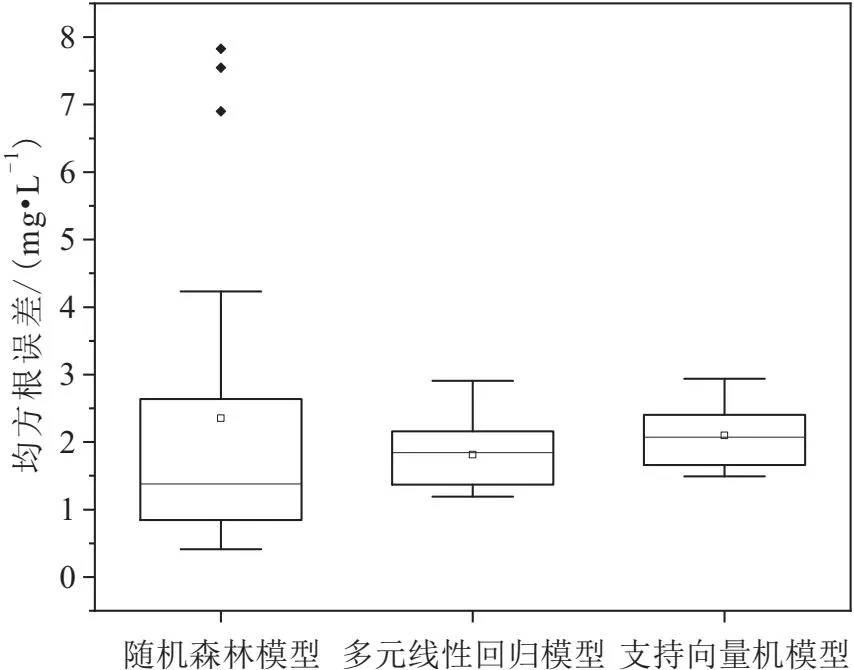
图4 随机森林模型、多元线性回归模型和支持向量机模型预测值的均方根误差箱形图Fig.4 Box plots of root-mean-square error for predicted values by random forest model,multiple linear regression model and support vector machine model

由图4可知,在测试集上,随机森林模型预测值的均方根误差变化范围在0.41 mg/L至7.83 mg/L(中值为1.38 mg/L)之间,而多元线性回归模型和支持向量机模型表现相对稳定,其预测值的均方根误差变化范围分别在1.19 mg/L至2.91 mg/L(中值为1.85 mg/L)和1.49 mg/L至2.89 mg/L(中值为2.07 mg/L)之间,其中随机森林模型的中值最小,表示其预测误差相对较小。这表明通过调整随机森林模型超参数能够获得预测性能更好的机器学习模型。