基于ThermaKin模型的环氧树脂热解反应动力学与热力学研究

陈湛文,丁 雁*,王鑫杨,龚俊辉,胡红云,方庆艳

(1.中国地质大学(武汉)工程学院,湖北 武汉 430074;2.南京工业大学安全科学与工程学院,江苏 南京 211816;3.华中科技大学煤燃烧国家重点实验室,湖北 武汉 430074)

20世纪中后期,环氧树脂材料被开发并投入生产使用[1-2]。自此,环氧树脂材料因自身优良的黏结性、耐腐蚀性、绝缘性和加工性能,在建筑、电气设备、航空等领域得到广泛的应用[3-7],成为各行业领域重要的树脂材料。然而,作为一种有机聚合物材料,环氧树脂材料具有可燃性[8-10],存在较大的火灾危险性[11-12],会对生产生活构成严重的威胁。在环氧树脂材料相关的火灾事故中,该类聚合物材料的热解是其燃烧过程的一个重要阶段,也是影响燃烧和火灾发展的关键因素[13]。因此,该类聚合物材料热解特性的研究一直是火灾安全领域的一项重要课题[14-15]。

环氧树脂材料热解特性的研究对火灾危险性评估具有十分重要的意义,且倍受研究人员的关注。为了探究环氧树脂材料的热解特性并研究该类聚合物材料的火灾防治手段,一些学者采取热分析方法对环氧树脂材料的热解和燃烧特性进行了试验和数值模拟研究。在试验方面,Chen等[16-17]利用热分析试验手段,探究了在氮气和不同氧浓度气氛下环氧树脂材料的热解特性,并对环氧树脂材料热解反应的表观活化能进行了预估;Ferdosion等[18]利用热重-红外光谱试验,分别对生物基环氧树脂材料和传统环氧树脂材料进行了对比试验分析,研究了两类环氧树脂材料的热解特性;Xiong等[19]通过对比两种不同固化剂固化的环氧树脂材料的热解特性,分析了不同固化剂对环氧树脂固化材料热稳定性的影响,并研究了不同升温速率下环氧树脂材料的热解机理;Wang等[20]选取碳纤维环氧树脂复合材料作为研究对象,通过锥形量热试验和热重试验等热分析手段,分析了不同加热条件对该材料质量损失率和热释放速率等热解和燃烧特性的影响。在数值模拟方面,Diao等[21]借助分子动力学模拟工具ReaxFF,分析了环氧树脂材料的热解特性,并考察了温度和升温速率对环氧树脂材料热解小分子产物演化的影响;Li等[22]借助相同的分子动力学模拟手段,建立了交联环氧树脂材料的热解模型,并考察了核量子效应对环氧树脂材料热解模型的影响。然而,环氧树脂材料的分子动力学模拟研究虽然较为精细地对其热解特性进行了数值模拟研究,但是分子尺度的模型难以直接应用于工程问题,因此许多研究学者从工程角度和更宏观的传热与传质尺度出发,建立了环氧树脂材料的热解模型。Tranchard等[23-24]根据碳环氧复合材料热分析试验数据,并借助商业软件SAMCEF,通过分析该材料的能量积累、热解及内部压力等,建立了碳纤维环氧树脂复合板材的热化学模型;李翰等[25]利用有限差分的方法,分析了碳纤维环氧树脂复合材料在受热过程的热响应规律。但是,这部分数值模拟研究更侧重于分析环氧树脂复合材料的传热过程,未能深入分析环氧树脂材料的热解机制。Stoliarov团队[26-31]根据聚合物热分析试验结果,提出了一种通过数值反演建立聚合物材料热解模型的方法,并开发了一款用于深入分析聚合物材料热解机制的模型工具——ThermaKin。目前,ThermaKin模型已被用于碳化[32-33]和非碳化[27]聚合物材料的热解特性研究,其模拟预测结果与试验数据基本吻合。但是,研究人员尚未借助ThermaKin模型对环氧树脂材料热解机制进行详细模拟和分析。

综上所述,有关环氧树脂材料热解机理的试验分析研究已较为丰富,但环氧树脂材料热解特性与机制的数值模拟研究仍有进一步深入与完善的空间。因此,本文针对目前市场常见的E-44环氧树脂材料,并选用腰果酚改性胺固化剂(PAA)材料对该环氧树脂材料进行固化,将腰果酚改性胺固化的环氧树脂(EP-PAA)材料作为研究对象,基于热重分析(TGA)和差示扫描量热分析(DSC)的试验数据,通过数值反演的方式,采用ThermaKin模型对选取的EP-PAA材料的热解特性进行数值模拟研究,并将模拟预测结果与试验数据进行了对比,以验证数值模拟预测结果的可靠性,进一步揭示环氧树脂材料的热解特性,为评估其火灾危险性提供依据。

1 材料与方法

1.1 试验样品

本研究选取的试验样品是腰果酚改性胺固化剂固化的环氧树脂材料。其中,样品所需的环氧树脂原料是中国石家庄文山凯绿葳化工有限公司生产的E-44型环氧树脂(EP),该类环氧树脂是双酚A型环氧树脂的一种,其环氧值为44。环氧树脂固化剂则是浙江万盛有限公司生产的腰果酚改性胺固化剂(PAA),其胺值为340～375 mg KOH/g,室温下其密度为0.97～0.99 g/cm3,活性氢当量为95[34]。

试验样品通过共混法制得:首先将E-44环氧树脂与腰果酚改性胺固化剂均匀混合,将该混合物置于100 mm×100 mm×10 mm的铝箔盒中,在室温下固化2 d;然后,将固化后的混合物静置14 d后进行粉碎,得到固化混合物粉末(EP-PAA);最后,在进行TGA和DSC等试验前,将样品在室温下干燥48 h。

1.2 试验方法

采用热分析试验仪器(Netzsch 449 F5 Jupiter STA同步热分析仪)进行TGA和DSC同步试验。试验所用坩埚是导热性能良好的铂铑坩埚,以确保试验测量的高灵敏度和准确性。仪器在试验前已完成所需的温度和灵敏度校准,以确保试验的准确性。

由于火焰覆盖下材料表面的热解区域氧浓度趋于零[35],所以试验将在无氧环境下观测样品材料的热解过程。本试验的具体操作流程如下:称取5～10 mg的样品放入铂铑坩埚,盖上开有一个直径0.25 mm小孔的坩埚盖,并将装有样品的坩埚置于仪器样品支架上的样品槽中,样品支架的另一槽中放置一个空坩埚作为参比坩埚;将样品设置在氮气气氛下的热解腔室进行热解试验,仪器通入的氮气流量为70 mL/min,其中包括热解腔室的吹扫氮气流量为50 mL/min,仪器保护气流量为20 mL/min。试验设置的升温程序为以10 K/min的升温速率,从313 K升至973 K。另外,在对样品进行试验之前需进行一次基线测试,该测试即在样品坩埚为空且其余试验步骤相同的情况下进行一次试验,以消除环境因素对试验观测的干扰,确保试验准确性。试验需重复进行3次,以避免试验的偶然性。

对于试验结果,按每1 K温度点取1个数据点来记录TGA和DSC的试验数据,并计算3次重复试验所得数据的平均值与误差值,同时对波动大的试验数据进行平滑降噪处理,以降低数据波动性。通过整理试验结果,得到了TGA试验的归一化质量(m/m0)和质量损失速率(MLR/m0)数据,以及DSC试验的归一化热流(normalized heat flow,NHF)和热流积分(integral heat flow,IHF)数据。m/m0为当前样品质量与初始样品质量的比值;MLR/m0是m/m0对时间进行求导后所得的样品质量损失速率。

2 ThermaKin模型简介

2.1 基本控制方程

EP-PAA材料热解模型的原理是基于TGA和DSC试验结果的数值反演,通过ThermaKin模型模拟分析材料热解的动力学和热力学过程。ThermaKin模型进行数值计算的基本控制方程如公式(1)和(2)所示,该两式表示一维模型设定下,材料热解过程的质量和能量守恒的控制方程。在ThermaKin模型中,材料是由热解过程各组分(反应物、中间产物、生成物等)组成,材料各组分的相关属性参数设为常数或与温度相关的表达式。ThermaKin模型的相关控制方程具体如下[26-27]:

(1)

(2)

(3)

θACOMA+θBCOMB→θCCOMC+θDCOMD+h

(4)

(5)

(6)

(7)

(8)

如公式(1)所示:等号左侧表示材料组分随时间的质量变化;等号右侧第一项表示热解反应中组分的消耗或生成量,该项所表示的热解反应的反应速率表达式如公式(3)所示;等号右侧第二项为气体组分的释放量,该项表示的气体释放的质量通量表达式如公式(5)所示;等号右侧的第三项表示材料发生膨胀或收缩所造成的质量变化。如公式(2)所示:等号左侧表示与材料比热容有关的显热变化;等号右侧第一项为与热解反应热有关的化学能变化,该项表示的反应热即为公式(4)中反应式的反应热h;等号右侧第二项、第三项和第四项分别表示热传导、外部热辐射和材料自身对环境辐射损失的热通量在x方向上的能量变化,这三项热通量参量的表达式分别如公式(6)、(7)和(8)所示;等号右侧第五项表示释放气体组分所导致的热损失;等号右侧第六项表示材料发生膨胀或收缩所造成的能量变化。

2.2 属性参量与边界条件的设定

基于TGA和DSC试验结果对材料热解特性进行数值反演时,为了贴近样品在试验中的实际温度变化,需进一步对样品温度变化速率进行拟合,从而更准确地获取模型所需的边界条件。本试验设定的0.083、0.167和0.333 K/s升温速率的拟合式如下[36]:

(9)

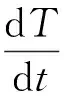
表1 升温速率拟合式参数

该升温速率拟合式与实际试验的升温数据曲线的拟合结果如图1所示。图1中的三角形散点、方形散点和星形散点分别表示样品在0.083、0.167和0.333 K/s升温速率下进行试验的升温数据曲线;虚线表示升温速率拟合式的拟合曲线。由图1可见,升温速率拟合式的拟合曲线与试验数据曲线基本吻合。

图1 升温速率试验数据与拟合曲线的对比Fig.1 Comparison of the heating rate test data and the fitting curves

由于EP-PAA试验样品质量小(毫克级别),试验过程升温速率较慢,样品与外部环境的升温过程几乎相同,所以将样品与外界热流的对流换热系数设为一个较大的值[105W/(m2·K)][26],以确保模型与试验样品的升温过程一致。初始材料的厚度设为1×10-5m,模型单元步长为1×10-5m,此时该模型中的样品材料仅为一个单元,亦可看作零维状态。ThermaKin模型求解的单位时间步长设为0.005 s,总时间步长设为4 500 s。在TGA和DSC试验中的样品可近似为热薄材料,即在样品内部的传热与传质传递过程可以忽略,故密度和导热系数的参数设为假设值[10-3kg/m3和0.3 W/(m·K)]。ThermaKin模型的数值求法为Crank-Nicolson法,该模型更详细的介绍可参考文献[26]。

3 结果与讨论

3.1 EP-PAA材料的TGA试验结果分析

图2表示0.167 K/s升温速率下样品的归一化质量(m/m0)和质量损失速率(MLR/m0)试验数据随温度变化的曲线。图2中试验数据的误差棒(所有试验结果图的误差棒均为试验数据平均值的置信区间)显示TGA试验的误差远小于真实值的5%。

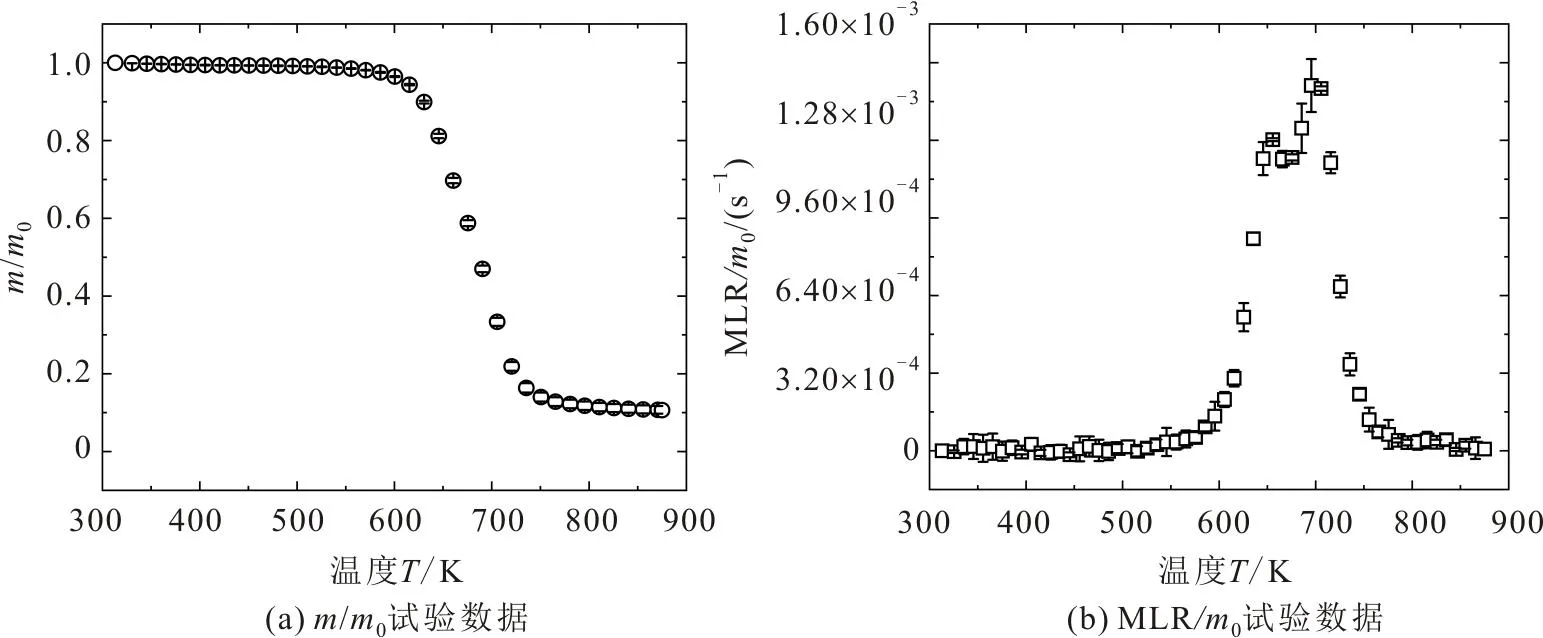
图2 EP-PAA材料TGA试验的归一化质量(m/m0)与质量损失速率(MLR/m0)随温度的变化曲线Fig.2 Experimental normalized mass loss (m/m0) and mass loss rate (MLR/m0) of TGA for EP-PAA

由图2(a)的TGA试验结果可知:样品热解残碳值为0.10(即最终的m/m0值);样品的m/m0试验结果曲线在温度为550～800 K时有明显的下降趋势,这表明样品因热解而发生明显热失重的过程主要集中于温度为550～800 K的区间。

由图2(b)可知:样品的MLR/m0试验结果在温度为550～670 K与670～875 K区间分别出现了两个对应的MLR/m0试验结果曲线峰(即质量损失速率峰),第一个质量损失速率峰在657 K(Tpeak1)达到峰值1.27×103s-1,第二个质量损失速率峰在703 K(Tpeak2)的达到峰值1.54×103s-1。这两个质量损失速率峰说明了EP-PAA样品的热失重可分为两个阶段。

3.2 EP-PAA材料的TGA试验数据的数值反演结果分析

基于EP-PAA材料的TGA试验数据曲线所呈现的两个阶段热失重特性,可将该材料的热解过程分为两个阶段。因此,本文针对EP-PAA的热解特性,提出了一个由2个一级反应与5个组分构成的热解反应机制。该材料的热解反应机制如表2所示。表2中:EP_PAA组分代表EP-PAA材料;EP_PAA_int组分为样品第一阶段热解反应(即反应1)的凝聚相中间产物;gas1组分为反应1的气体产物;EP_PAA_res组分则为样品第二阶段热解反应(即反应2)的残碳产物;gas2组分是反应2的气体产物。反应1和2的化学计量数分别由样品的MLR/m0试验数据曲线中两个质量损失速率峰之间的最低点与第二个质量损失速率峰末尾最低点所对应的m/m0值确定。反应的动力学参数初估值(活化能Ea和指前因子A)可基于试验数据与下式计算得到[38]:

表2 EP-PAA材料的热解反应机制及其动力学参数和反应热参数

(10)

式中:e为自然常数,2.718;MLRpeak/m0表示样品在TGA试验中MLR/m0数据曲线的峰值(s-1);Tpeak为样品MLR/m0试验数据峰值所对应的温度(K);m0为样品的初始质量(kg)。

利用Fiola等[39]提出的爬山优化子程序对Ea、A和θ参数的初估值进行优化,可得到模型所需的准确反应动力学参数。该优化算法的结果评判准则是该模型模拟计算所得的样品残碳值(m/m0)、质量损失速率(MLR/m0)峰值与TGA试验结果的误差均小于5%,且MLR/m0峰值对应温度与试验结果的差值不超过5 K。优化所得到EP-PAA材料的热解反应动力学参数如表2所示。

根据提出的热解反应机制,利用ThermaKin模型,模拟计算EP-PAA材料的热解过程,得到如图3所示的模型求解结果。图3中的圆形散点和方形散点分别代表样品TGA试验的m/m0和MLR/m0结果,实线表示样品m/m0和MLR/m0的模拟结果。由图3可见,EP-PAA材料的残碳值、MLR/m0峰值及其峰值对应温度的模拟结果与前述的结果评判标准相符,表明建立的热解反应机制可以用来准确模拟EP-PAA材料热失重过程的热解特性。

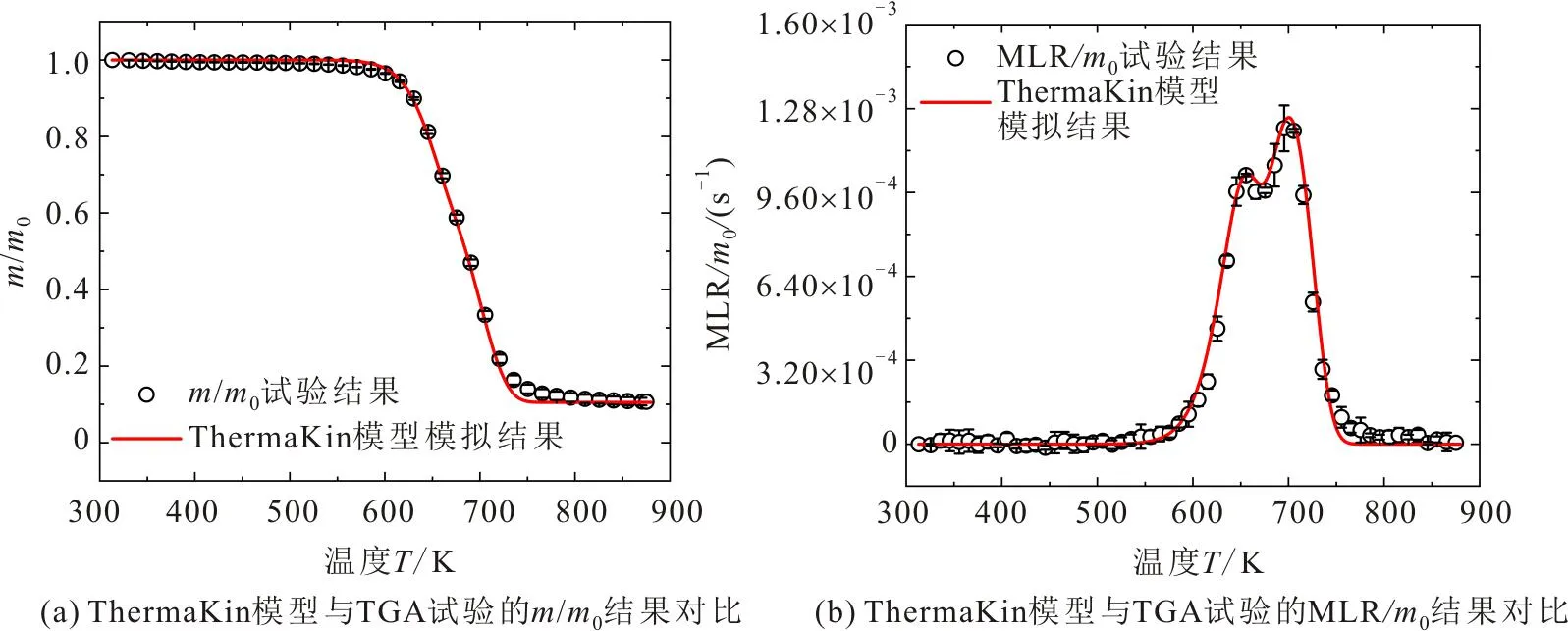
图3 EP-PAA材料的m/m0和MLR/m0ThermaKin模型模拟结果与TGA试验结果的对比Fig.3 Comparison of ThermaKin model simulated results and TGA experimental results on m/m0 and MLR/m0 for EP-PAA

3.3 EP-PAA材料的DSC试验结果分析

EP-PAA材料DSC试验的归一化热流(NHF)试验结果是由试验仪器测量的热流除以样品初始质量后换算所得;EP-PAA材料DSC试验的归一化热流积分(IHF)试验结果是由NHF试验数据进行时间积分所得。NHF与IHF随温度的变化曲线见图4。

图4 EP-PAA材料DSC试验的归一化热流(NHF)和热流积分(IHF)随温度的变化曲线Fig.4 Normalized heat flow (NHF) and integral heat flow (IHF) experimental results of DSC for EP-PAA

由图4(a)可知:

1) 在温度为313～<613 K区间,当温度为313～<400 K时样品的NHF试验数据曲线出现较为明显的热流值上升(NHF值为正表示吸热,反之为放热),这是由样品因升温而吸热所引起的显热变化所致;当温度为400 K时,NHF试验数据曲线出现了一个转折峰;当温度为400～<522 K时,样品的NHF试验数据曲线出现了下降趋势;当温度为522～<613 K时,NHF试验数据曲线在热失重发生前后出现一个小型吸热峰。上述曲线特征可能与EP-PAA材料自身的物理特性有关[40]。

2) 在温度为613～<830 K区间,样品的NHF试验数据曲线出现了一个明显的主吸热峰,其峰值达到0.53 W/g,该主吸热峰与图2的MLR/m0峰出现在相同的温度区间。

3) 当温度达到830 K后,样品的NHF试验数据曲线出现“尾部上翘”的现象,其原因为试验仪器在该高温区域的测量准确度大大降低,导致NHF试验数据曲线的测量受到干扰。

由图4(b)可知:样品DSC试验的IHF试验数据曲线随温度的升高呈上升趋势,在温度达到800 K以后其上升趋势更为平缓。这是因为在温度达到800 K之后,EP-PAA材料热解反应已接近完成,且此时样品热解产生的残碳的比热容值较小。

3.4 EP-PAA材料的DSC试验数值反演结果分析

通过对EP-PAA材料热解特性的分析可知,DSC试验得到的NHF数据由两部分组成[37]:第一部分是EP-PAA材料热解过程中各组分固相产物吸热所带来的热流变化,即与比热容相关的显热变化;第二部分是EP-PAA材料热解过程中反应热所带来的热流变化,即与反应热有关的化学能变化。EP-PAA材料NHF数据的计算表达式如下[27]:

(11)

式中:V表示样品的体积(m3);Nc表示组分总数;Nr表示反应总数;其余符号所表示的含义同上。

根据公式(11)和图4的DSC试验结果,可得到表2中热解反应机制的各组分比热容参数。如图4所示,样品NHF试验数据曲线在温度为313～550 K区间出现明显的转折波动,且样品在该温度区间未发生热失重,这一现象表明样品在该温度区间发生了与EP-PAA材料比热容相关的显热变化。因此,EP_PAA组分的比热容参数需设为一个关于温度的分段表达式,以确保ThermaKin模型能够准确地模拟样品在DSC试验过程的热流变化。EP_PAA组分比热容参数的计算流程如下:

1) 通过将温度为313～<400 K时样品的NHF试验数据除以对应温度区间的升温速率与样品m/m0试验数据的乘积,再将计算得到的商值数据进行线性拟合,得到一个关于温度的线性表达式,该表达式即为反应1中EP_PAA组分比热容参数的第一段线性表达式。

2) 通过选取温度为400～550 K时样品的NHF试验数据,以相同的方法计算商值数据并进行线性拟合,可求得EP_PAA组分比热容参数的第二段线性表达式。

3) 需要说明的是,固相组分的比热容表达式可以通过样品NHF试验数据的非线性拟合方式获取,但模型计算精确度要求在线性拟合情况下已得到满足。另外,由于TGA和DSC试验的样品可以近似为热薄材料,并不需要考虑其内部的传热传质过程,同时可近似认为热解气体产物生成后立即离开固体表面,因而可以忽略气体组分比热容对试验结果的影响。(gas1和gas2组分比热容均假设为1 000 J/(kg·K)。

4) 由于EP-PAA材料热解后所得残碳(EP_PAA_res组分)的比热容难以直接测量,其比热容可认为是常见碳化材料热解残碳的平均值,即为1 700 [J/(kg·K)][32,36,41-42]。

5) EP-PAA材料热解反应的中间产物(即EP_PAA_int组分)的比热容可近似为EP_PAA组分第二段比热容与EP_PAA_res组分比热容的均值。这一做法的原因是EP_PAA_int组分存在于两个热解反应(反应1和反应2)过程中,该组分的比热容无法直接测量或通过DSC试验的NHF数据直接求取,仅能看作是反应1的反应物(EP_PAA组分)与反应2的产物(EP_PAA_res组分)比热容均值。

通过上述求解方法得到的EP-PAA材料各组分比热容的取值如表3所示。

表3 EP-PAA材料热解反应机制中凝聚相组分的比热容

根据公式(11)和表2的热解反应机制,代入获取的相关属性参量,通过ThermaKin模型进行数值模拟,得到如图5所示的模拟结果。图5(a)和图5(b)中的方形散点分别表示DSC试验的NHF和IHF数据;虚线表示当前输入参量下模型(model_base)的求解结果。

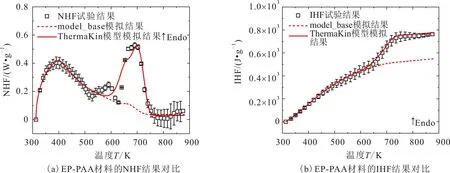
图5 EP-PAA材料的ThermaKin模型模拟结果与DSC试验结果的对比Fig.5 Comparison of ThermaKin model simulated results and DSC experimental results for EP-PAA

由图5可知:在温度低于550 K时模型求解结果与DSC试验结果吻合;但在温度为550 K后,模型求解结果小于DSC试验结果,这一误差的原因是,当前输入参量下模型求解的结果仅考虑了公式(11)中与样品比热容有关的显热项,即此时ThermaKin模型的反应热参数h为0。

为了使EP-PAA材料的模型求解结果与DSC试验结果相符,需要进一步获取热解反应机制的反应1和2的h值。h参量的初始值计算方法如下:

(12)

上式中:h1和h2分别表示反应1和2的反应热(J/kg);下标T1、T2和T3分别代表温度550、670和850 K,这三个温度点分别表示反应1和2的开始温度点及反应结束温度点(由于试验的MLR/m0数据在温度为850 K时近似为0,可认为此时热解基本结束);IHFMB_T1、IHFMB_T2、IHFMB_T3、IHFExp_T1、IHFExp_T2和IHFExp_T3分别表示T1、T2和T3对应的model_base模型求解结果与试验结果的IHF数据;θ1表示反应1的化学计量数,即为0.7。

通过计算得到的反应1和2的h初始值仍需不断迭代优化,比对DSC试验结果,优化得出h取值。优化结果评判准则是该模型进行数值反演所得的IHF值、NHF曲线主峰值与DSC试验结果的误差小于10%,且主峰值对应的温度点与DSC试验结果相差不超过10 K,最终优化得到的反应1和2的h取值如表2所示(吸热为正)。

图5中的实线表示在model_base的基础上,模型引入表2中h值所得到的模拟结果。图5中,引入h值的模型最终模拟结果与前述的结果评判标准相符,但是在温度为530～610 K时模型最终模拟结果与试验结果存在误差。误差体现在模型最终的模拟结果未能准确地拟合DSC试验中NHF数据曲线在该温度区间出现的一个小型吸热峰。

该误差出现的原因有两个:①由于同步热分析仪受环境干扰的影响较大,DSC试验数据本身存在较大的误差。特别在进行DSC试验时,仪器所测量的热流值偏小的情况下,试验测量更容易受到外界的干扰而产生较大的误差。②由于温度为530～610 K时NHF数据曲线的小型吸热峰横跨未发生热失重与发生热失重的温度区间,表明样品在该温度区间可能发生了一系列失重不明显的复杂热解反应,因此本模型的模拟结果难以精确捕捉这一复杂的热解过程。

3.5 不同升温速率下的试验结果预测与模型验证

基于前文构建的热解模型,分别对低升温速率(0.083 K/s)和高升温速率(0.333 K/s)条件下EP-PAA材料的热解反应过程进行预测。图6(a)为0.083 K/s升温速率下模型预测结果与TGA试验结果的对比曲线;图6(b)为0.333 K/s升温速率条件下模型预测结果与TGA试验结果的对比曲线。图6中:圆形散点和方形散点分别表示样品的m/m0和MLR/m0试验数据随温度的变化曲线;实线表示m/m0和MLR/m0的ThermaKin模型预测结果随温度的变化曲线。

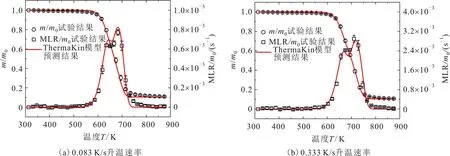
图6 EP-PAA材料在0.083 K/s和0.333 K/s升温速率条件下ThermaKin模型预测结果与TGA试验结果的对比曲线Fig.6 Comparison of ThermaKin model predicted and experimental results of TGA at the heating rate of 0.083 K/s and 0.333 K/s for EP-PAA

由图6可知:0.083 K/s升温速率条件下的残碳值和质量损失速率峰值的ThermaKin模型预测结果与TGA试验结果的误差均小于5%,且其质量损失速率峰值对应温度点的ThermaKin模型预测结果与TGA试验结果的差值小于5 K;0.333 K/s升温速率条件下的残碳值和质量损失速率峰值的ThermaKin模型预测结果与TGA试验结果的误差分别小于5%和8%,且其质量损失速率峰值对应温度点的模型预测结果与TGA试验结果差值小于5 K。上述模型预测误差结果说明了本文建立的热解模型能够准确地模拟预测EP-PAA材料宽升温速率条件范围下的热解特性。总体而言,在不同升温速率条件下,该热解模型对EP-PAA材料热解特性的预测结果具有较高的准确性和可靠性。

4 结 论

1) 根据TGA试验结果分析,EP-PAA材料的热失重过程主要集中于温度为550～800 K的区间,且其质量损失速率峰呈双峰分布。基于EP-PAA材料的TGA试验结果,建立该材料热解模型的热解反应机制。EP-PAA材料的热解反应机制由两步一级反应组成。

2) 根据DSC试验结果分析,研究了EP-PAA材料在热解试验过程的热流变化,发现EP-PAA材料在热解试验过程发生的热流变化,与热失重过程具有较强的同步性与相关性。

3) 通过对EP-PAA材料在0.167 K/s升温速率条件下的TGA和DSC试验结果进行数值反演,获得了构建热解反应模型所需的反应动力学参数、反应热和各组分的比热容参量。结合两步一级热解反应机制与数值反演获取的相关参量,对EP-PAA材料在TGA和DSC试验的热解过程进行模拟,分析了该材料的热解特性。模拟结果与TGA和DSC试验结果总体吻合,且模拟结果的误差均在合理范围之内。

4) 构建的热解反应模型能够准确地模拟预测低升温速率(0.083 K/s)和高升温速率(0.333 K/s)条件下EP-PAA材料的热解试验结果:低升温速率和高升温速率下TGA试验的残碳值和质量损失速率峰值的预测误差分别小于5%和8%,且其质量损失速率峰值对应温度点的模型预测结果与试验结果差值小于5 K。这一结果验证了该模型的可靠性和准确性。

致谢:感谢中国地质大学(武汉)“地大学者”人才岗位科研启动经费资助项目(2020088)和华中科技大学煤燃烧国家重点实验室开放课题基金(FSKLCCA2207)的支持,以及美国马里兰大学帕克分校Stanislav I.Stoliarov教授的帮助。