基于激光雷达的非合作航天器姿态测量
2024-02-24冯志辉南亚明
冯 田,冯志辉,南亚明,雷 铭
(1.中国科学院空间光电精密测量技术重点实验室,四川 成都 610209;2.中国科学院光电技术研究所,四川 成都 610209;3.中国科学院大学,北京 100049)
0 引言
空间非合作目标是指未安装光学辅助测量装置的目标航天器[1]。对非合作目标的姿态测量是航天器相对导航、交会对接进而实施在轨服务或者太空垃圾清理等任务的前提[2],对推动航天技术进步具有重要意义。
非合作目标姿态测量主要有两类技术路线:1)基于视觉的测量[3],利用单目或双目相机对目标成像,结合图像处理算法解算相对姿态;2)基于激光雷达(LiDAR)的测量[4],利用LiDAR等主动光学敏感器获取目标三维点云,再由点云处理算法解算姿态。太空环境光照条件较为恶劣,相机系统难以连续获得高质量图像,LiDAR等主动光学成像系统通过计算激光回波信号实现测量,受到目标运动状态、光照影响较小,易于全天候长时间稳定观测与跟踪。近年来,许多学者在点云配准[5]框架下提出了点云投影[6]、点法向量[7]、卡尔曼滤波[8]、模型匹配[9,10]等姿态测量方法,但现有方法存在一些急需解决的问题。首先是在交会对接过程中,LiDAR只能从单一视角获取点云数据,目标自遮挡会导致点云结构不全,现阶段的姿态测量算法对点云质量要求较高,点云结构不完整会对点云配准精度造成较大影响[11]。其次是现有配准算法计算效率较低[12],计算速度不能满足在轨实时测量的要求。
针对目标自遮挡导致的姿态解算困难以及点云配准算法效率较低等问题,本文开展对姿态估计算法的研究,提出了一种基于LiDAR三维点云的非合作目标姿态测量方法,并对所提方法进行了实验验证。
1 姿态测量算法
1.1 算法总体设计
为便于解算目标航天器姿态,建立目标航天器坐标系(Ot-XtYtZt),LiDAR 坐标系(Os-XsYsZs)以及世界坐标系(O-XYZ),目标航天器基准点云主轴方向为(O0-X0Y0Z0),第i时刻目标点云主轴方向为(Oi-XiYiZi),目标航天器分别绕X0,Y0,Z0轴旋转时如图1所示。

图1 交会对接空间坐标系示意
由图1可以知道,通过求解目标点云与基准点云的空间变换关系即可解出目标姿态信息。因此,本文通过对目标模型进行地面数据采集将对接姿态目标航天器的点云数据存储于追逐航天器计算机,将姿态测量问题转化为目标点云与基准点云的配准问题。目标点云空间变换可以分解为旋转变换和平移变换,目标航天器三维点云的变换矩阵由式(1)给出
式中 R为旋转变换矩阵,T为平移变换矩阵,V为视变化因子,S为比例缩放因子。其中,旋转矩阵R可以分解为滚转、俯仰、偏航轴旋转矩阵
对于按照Z 轴、Y 轴、X 轴旋转顺序进行的变换,总的旋转变换关系R为
基于上述分析,本文将姿态测量方法分为初始姿态获取和快速姿态跟踪两部分,初始姿态获取阶段利用特征点云的分割与匹配解决目标自遮挡导致的点云配准困难问题,在姿态跟踪阶段提出一种快速点云配准算法实现姿态实时跟踪测量,该方法流程如图2所示。
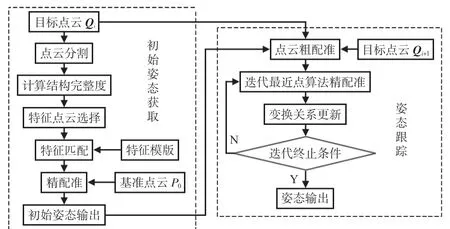
图2 本文所提方法的流程
1.2 初始姿态获取算法
目标航天器通常为失效或故障的卫星[13],通过观察空间结构可以发现,卫星主要有:卫星主体、通信天线、太阳能帆板三大部分,且具有不同的结构特征,如图3 所示。依据结构特征可以实现对关键特征的分割和识别,再利用关键特征与模板匹配获得初始变换矩阵。

图3 卫星结构特征示意
1.2.1 点云分割
首先提取特征比较明显的太阳能帆板,通过提取点云平面可以分割出帆板的点云数据。以随机采样不断提出局外点的方式分割点云,分割步骤如下:
1)设定算法随机点选取次数t,然后在目标三维点云数据中随机选取初始点分别为p1(x1,y1,z1),p2(x2,y2,z2),p3(x3,y3,z3),再以初始点确定一个平面并计算平面法向量
2)计算任意一点pi(xi,yi,zi)到该平面距离
3)设定阈值τ,对于di<τ的点云数据判定为平面中的点,将符合条件的点云保存下来,并记录点的数量。
4)重复步骤(1)~步骤(3),将点数量最多的点云保存下来作为帆板特征。
结合通信天线曲面特征明显的特点,采用曲率聚类分割的方法,具体实现步骤如下:
1)计算点主曲率,再基于主曲率对点云进行排序选取种子点,通过最小二乘法拟合构建二次曲面求解点曲率,以点pi为邻域中心,半径为r的球体空间内的邻域点构建二次曲面M,曲面方程为
其中,a,b,c为二次曲面系数,根据最小二乘原理,二次曲面系数使得式(7)取最小值
式中 xi,yi,zi为邻域点坐标;通过对式(7)求偏导并使偏导数为零,可以求解最佳拟合曲面的参数a,b,c的值
曲面M在点pi处的一阶、二阶偏导数为
曲面M在点pi处的法向量表示为
根据曲面第一、二基本公式计算曲面M 的第一、二基本量
高斯曲率和平均曲率为
主曲率为
2)设定种子集合S,聚类集合O,对点曲率进行分析,若曲率大于阈值,则放入S中作为种子点;然后将该点的邻域点放入集合O。
3)若S为非空集合,重复步骤(2),直到S为空集,保存点数量最多的聚类集合。
1.2.2 点云特征匹配
经过太阳能帆板和通信天线的分割、识别后,将目标点云剩余部分识别为卫星主体特征。以特征置信概率来表示特征结构完整度,计算特征置信概率并进行排序来选择保存结构最完整的特征点云,置信概率计算方式为
式中 psolar_panel,pantenna,pmain分别为太阳帆板特征、通信天线特征、卫星主体特征的置信概率;N为对应特征点云的点数量。
模拟地面预存储目标卫星的特征模板,将模型区间设定为π/2,即分别以X,Y,Z 轴旋转π/2,π,3π/2,2π 采集特征点云,共计64 组特征模板;以最近点距离平方和作为评价参数,以距离最小的模型姿态计算初始变换矩阵R0,T0。然后对目标点云和基准点云P0应用迭代最近点(iterative closest point,ICP)算法精配准,计算初始姿态获取变换矩阵Rorigin,Torigin;最后结合式(3)解算初始姿态信息。
1.3 姿态跟踪算法
为实现对目标航天器的实时姿态跟踪,本文提出一种改进的点云配准算法实现快速点云配准。对两帧点云进行主成分分析提取特征向量,通过计算特征向量变换关系获取粗配准矩阵,然后利用KD-tree最近邻搜索提高对应点搜索效率对ICP算法进行改进,完成精配准。
点云粗配准通过对点云主成分分析提取点云特征向量,然后依据特征向量建立粗配准变化关系,实现步骤如下:
1)计算样本重心。以第i时刻点云Qi为例,重心坐标计算方式为
2)计算协方差矩阵,如式(16)所示
3)特征值分解。对协方差矩阵奇异值分解取前3 个方差最大特征值对应的特征向量
同理,第i +1点云Qi+1重心及特征向量
4)建立特征向量变换关系
5)利用旋转矩阵R0和平移矩阵T0对点云进行转换,完成粗配准。
精配准阶段应用改进的ICP 算法来提高点云配准效率。根据ICP算法的原理可以分析到,该算法是对整个点云数据逐一寻找对应关系,计算效率较低[14]。为提高精配准计算速度,本文采用基于k 维二叉树的最近邻搜索改进ICP算法的对应点搜索策略,具体步骤分为二叉树搜索和回溯查找,改进ICP算法配准步骤如下:
1)配准初始化。输入经过粗配准的源点云Qi+1和目标点云,建立点云KD-tree,设置最大迭代次数imax、误差阈值efinal和单次迭代误差变化阈值εfinal。
2)对应点搜索。首先从根节点开始按照目标点与各个节点的比较结果向下访问KD-tree,直至到达叶子节点。然后回溯搜索路径,判断其他子节点空间是否有更邻近的节点,如果存在则进入其他子节点空间进行搜索,直至搜索路径为空。
3)求解变换矩阵。依据步骤(2)所得的对应点关系,求解当次迭代对应的旋转矩阵Ri和平移矩阵Ti,更新误差函数值,得到配准误差ei和本次迭代误差变化值εi。
4)更新点集并判断迭代条件。重复步骤(2)~步骤(3),直至满足任一迭代结束条件:配准误差小于阈值、单次迭代误差变化值小于阈值、或者迭代次数大于最大迭代次数,得到最终的变换矩阵[R,T],进而解算目标姿态角。
2 实验结果与分析
实验通过3D打印卫星模型,利用三维转台模拟卫星转动,使用16线LiDAR采集目标的三维点云信息,使用仿真软件做算法运行与姿态解算,运行于Intel®CoreTMi5—8250U@1.6 GHz的CPU、8 GB内存、64 位Windows10 操作系统的计算机上,实验平台如图4所示。

图4 卫星模型姿态测量
卫星模型实测实验首先模拟地面对在轨目标的基准点云预建立,即地面采集目标模型的基准点云并建立特征点云模板库。通过LiDAR在目标±X,±Y,±Z方向的6个视角采集卫星模型点云数据,然后进行分割、融合等作为基准点云。随后在不同的姿态角采集点云建立特征模板库。然后模拟在轨服务任务中交会对接最终逼近段对目标航天器的姿态测量,由LiDAR 采集目标点云数据,并依据本文所提算法进行姿态解算。
在第一组实验中,利用六自由度转台作为控制模块,控制精度在微弧度量级。具体实验方案如下:使用三维转台控制模型分别绕X,Y,Z轴旋转,转动范围为(-10°,10°),每5°采集点云数据,共计125个初始姿态测量数据。然后应用本文所提初始姿态获取算法进行姿态解算,验证初始姿态获取算法的精度,每次测量平均姿态误差计算结果如图5所示。
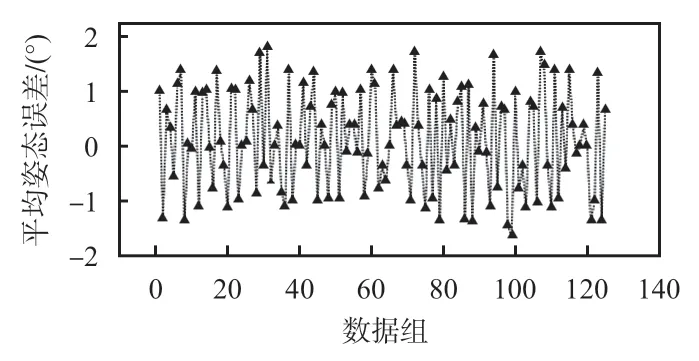
图5 初始姿态获取实验结果
由图5可以知道,本文所提初始姿态估计算法在不同姿态具有稳定姿态解算能力,平均初始姿态估计误差小于1.5°。然后将初始姿态角度分别设定为(0°,0°,0°),(-10°,-10°,-10°),(-5°,-5°,-5°),(5°,5°,5°),(10°,10°,10°)进行初始姿态测量,然后在三维转台量程范围(-10°,10°)随机设置三维姿态进行姿态跟踪实验,每组实验跟踪姿态变换20 次,共125 个姿态测量数据,测量结果如图6所示。
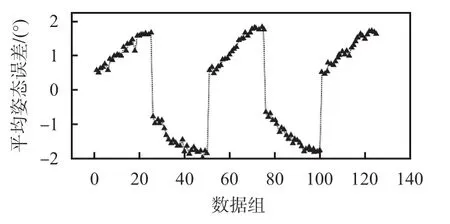
图6 姿态测量实验结果
从图6中可以看出,本文所提姿态估计算法具有较高鲁棒性,姿态测量误差小于2°,姿态跟踪精度建立在初始姿态估计的基础上,并且随着跟踪时间的增多,会积累一定累计误差。
在第二组实验中,机械转台控制卫星模型绕Z轴360°旋转测量。试验方案如下:机械转台控制卫星模型转动,角度范围(-360°,360°),分布将初始姿态设置为(0°,0°,0°),(0°,0°,60°),(0°,0°,120°),(0°,0°,180°),(0°,0°,240°),(0°,0°,360°),在姿态区间间隔5°采集目标点云进行姿态测量与跟踪,共计72个测量数据,测量结果如图7所示。

图7 绕Z轴旋转姿态测量结果
从图7中可以看出,姿态测量误差的分布依然表现出受初始姿态估计精度影响,存在累计误差的特点,LiDAR从侧面获取目标点云时结构完整度降低姿态误差变大。但对绕Z轴旋转过程中的姿态测量表现出足够的鲁棒性。
3 结论
本文面向空间交会对接任务中LiDAR 对模型已知非合作目标姿态测量需求,针对目标自遮挡导致点云配准性能差等问题提出了一种基于LiDAR 的非合作目标姿态测量方法。通过点云特征分割与匹配鲁棒地获取目标初始姿态,再结合快速点云配准算法实现姿态跟踪。搭建卫星模型姿态测量平台对所提方法进行实验验证,实验结果表明:本文方法能够稳定完成姿态测量。
