长沙至衡阳低真空管道磁浮线路方案动力性能评估

2024-02-23黄成名杨文东王英杰鲍慧明张继鹏

铁道勘察 2024年1期

黄成名杨文东王英杰鲍慧明张继鹏

(1.中铁工程设计咨询集团有限公司,北京 100055; 2.北京交通大学土木建筑工程学院,北京 100044)

引言

低真空管道磁浮交通系统利用封闭管道创造一个万米高空量级的低气压环境来减少车辆高速运行时的空气阻力,同时利用磁浮技术实现车体悬浮与推进来降低车辆与轨道间的摩擦阻力和车轨冲击,从而使车辆运行速度超过1 000 km/h。该系统结合了轮轨高速系统和航空系统的优点,在民用和军用领域均具有重大研究价值[1-4]。

目前,已有不少学者采用车线系统动力学模型对线路设计方案开展动力学评估。刘磊建立2动1拖的3节高速列车编组模型,仿真计算列车以350,400 km/h等速度通过不同曲线时的安全性和平稳性指标,并给出高低速列车共线和不共线条件下最小曲线半径推荐取值[5];袁伟以某海外高速铁路为例,利用车线系统动力学模型对比分析原线路设计方案与优化后的行车动力性能指标[6];时瑾等建立高铁动车-线路动力学仿真模型,计算动车以400 km/h速度通过某既有350 km/h线路时的安全性和舒适性指标,分析现有350 km/h线路开行400 km/h高速列车的可行性[7];谢毅等以标准动车组为原型建立车线耦合动力学模型,从安全性和舒适性的角度出发对新建沪渝蓉高速铁路重庆至成都段线路进行动力学评估[8];翟婉明等建立车辆-轨道空间耦合动力学模型,研究400 km/h条件下平面曲线参数匹配建议取值[9]。针对中低速磁悬浮线路,葛亮以长沙磁浮试验线为例,利用运动学原理结合行车模拟,确定试验线合理长度及平纵断面设计参数[10];陈志贤等建立中低速高温超导磁悬浮车辆动力学仿真模型,分析车辆曲线通过性能,并在此基础上对悬浮架结构方案进行优化[11]。针对高速磁悬浮线路,WANG等建立高速磁浮车辆-曲线轨道梁耦合模型,以曲线最短长度为目标、乘客舒适度限值为边界条件研究平面曲线参数选择[12];YUAN等采用UM软件建立高温超导(HTS)车辆-桥梁耦合模型,并对比分析EMS、EDS磁浮车辆动力性能[13]。针对超高速磁悬浮线路,DENG等在西南交通大学高温超高磁浮试验线上对磁悬浮车辆运动稳定性及非线性振动等特性进行研究[14-15];吴昊从舒适度指标出发研究影响平面曲线参数的因素,计算曲线半径及缓和曲线长度取值,并利用刚体运动学理论对支撑力和导向力进行分析[16]。综上所述,采用车线动力学手段对线路参数及线路方案进行评估可有效反映车辆通过曲线时的动力性能。然而,目前缺乏对低真空管道超高速磁悬浮线路方案动力学评估方面的研究。

以下在前人的研究基础上,在京广通道上选取长沙至衡阳段开展线路方案研究。基于车线系统动力学理论,采用低温超导电动悬浮制式,建立低真空管道磁浮车辆-线路动力学模型,计算超高速磁悬浮车辆通过长沙至衡阳段线路时的车辆动力性能指标,从时程曲线和频数统计方面进行分析。以期为真空管磁悬浮交通系统的建设和运营提供理论依据。

1 车辆-线路动力学模型

1.1 车辆模型

采用多体动力学软件Simpack建立真空管磁悬浮车辆三维空间模型。车辆模型由1个车体、2个转向架组成,其中车体与转向架之间由二系悬挂弹簧连接。每个转向架包含2个H构架,每个H构架又有12个电磁铁。电磁铁安装在H构架两侧的纵梁下,纵梁和电磁铁之间由一系列悬挂弹簧连接。电磁力通过阻尼弹簧模拟,弹簧侧向压缩提供导向力,垂向压缩提供悬浮力。在建模过程中将车体、转向架和H构架等部件视为刚体,车体和转向架考虑纵向、浮沉、横移、侧滚、点头及摇头自由度,H构架横梁考虑侧滚自由度,H构架纵梁考虑点头自由度,电磁铁考虑纵向、浮沉、横移自由度。因此,真空管磁悬浮车辆模型共有174个自由度,真空管磁悬浮车辆模型示意见图1。

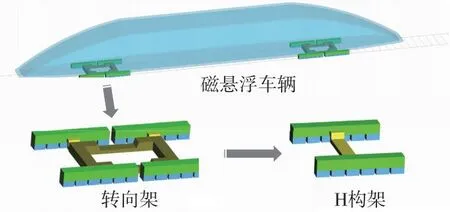
图1 真空管磁悬浮车辆模型Fig.1 Schematic diagram of the vacuum tube maglev vehicle model

1.2 线路不平顺模型

目前缺少低真空管道超高速磁悬浮实测不平顺数据,故施加高速磁浮铁路线路不平顺作为激励[17],不平顺功率谱密度为

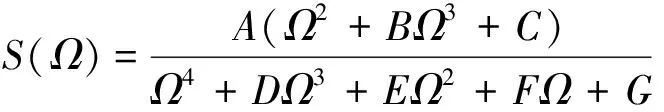
(1)

式中,S(Ω)为功率谱密度;Ω为空间频率;A、B、C、D、E、F、G均为功率谱特征参数;不平顺功率谱密度参数见表1。

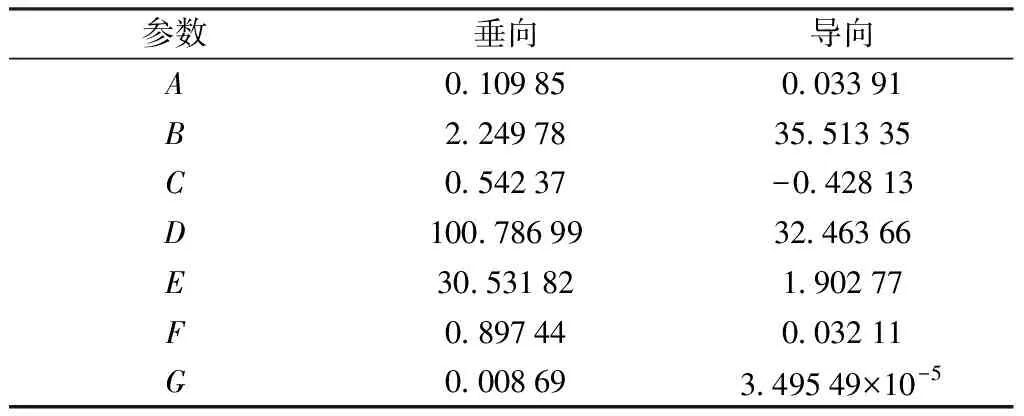
表1 不平顺功率谱密度参数

2 长沙至衡阳线路方案及动力学评价指标

长沙至衡阳超高速磁悬浮试验线长度为161.86 km,最高设计速度为1 000 km/h,长沙至衡阳线路方案示意见图2。

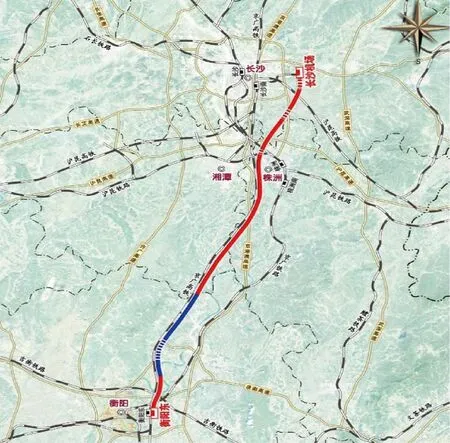
图2 长沙至衡阳线路方案示意Fig.2 Schematic diagram of Changsha to Hengyang route

该线路方案由7段曲线组成,曲线半径为15 000～30 000 m,缓和曲线长度均为1 400 m,长沙至衡阳线路参数见表2。此外,圆曲线横坡为16°,车辆运行速度为1 000 km/h。

表2 长沙至衡阳线路参数

借鉴现有磁浮铁路技术标准、高速铁路设计规范中有关舒适性的规定[18-20],选取车体垂向和横向加速度作为动力学评价指标,动力学评价指标及限值见表3。

表3 动力学评价指标及限值 m/s2

3 动力学评价分析

3.1 时程曲线分析

利用所建模型,计算得到车辆在该段线路上运行时车体垂向加速度、横向加速度响应及前转向架一位电磁铁的悬浮力和导向力。

(1)车体垂向加速度

计算得到磁浮车辆车体垂向加速度时程曲线(见图3)。

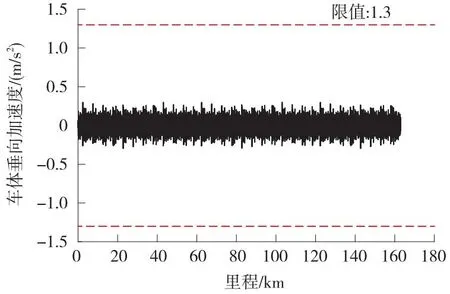
图3 车体垂向加速度时程曲线Fig.3 Time history curve of the carbody vertical acceleration

由图3可知,车体垂向加速度幅值不超过0.5 m/s2,均在限值1.3 m/s2以内,满足舒适性要求;车体垂向加速度变化总体平稳,没有出现突变现象。

(2)车体横向加速度

计算得到磁浮车辆车体横向加速度时程曲线(见图4)。

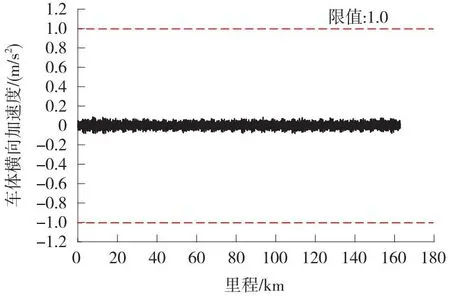
图4 车体横向加速度时程曲线Fig.4 Time history curve of the carbody lateral acceleration

由图4可知,车体横向加速度幅值不超过0.2 m/s2,均在限值1.0 m/s2以内,满足舒适性要求;车体横向加速度变化总体平稳,没有出现突变现象。

(3)悬浮力

计算得到前转向架一位电磁铁左右侧悬浮力时程曲线(见图5)。

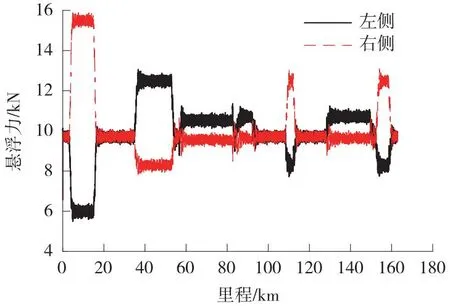
图5 悬浮力时程曲线Fig.5 Time history curve of the levitation force

由图5可知,悬浮力在直线段上均值约为10 kN,曲线段上幅值普遍不超过16 kN,最大值出现在曲线1上,为15.9 kN;在直线和圆曲线间过渡平滑,说明缓和曲线长度设置合理。

(4)导向力

计算得到前转向架一位电磁铁左右侧导向力时程曲线(见图6)。

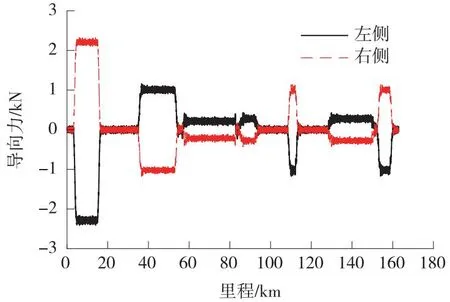
图6 导向力时程曲线Fig.6 Time history curve of the guiding force

由图6可知,导向力在直线段上幅值小于0.5 kN,曲线段上幅值不超过3 kN,最大值出现在曲线1上,为2.3 kN;在直线和圆曲线之间过渡平滑,说明缓和曲线长度设置合理。

以上时程曲线结果表明,车辆在直线和圆曲线上运行时各项动力性能指标较小,车辆振动加速度满足限值要求,缓和曲线长度设置合理。

3.2 统计频数分析

(1)动力学指标分布情况

对所计算的车体垂向加速度时程曲线进行统计,得到其在不同数值区间上的频数分布,见图7。

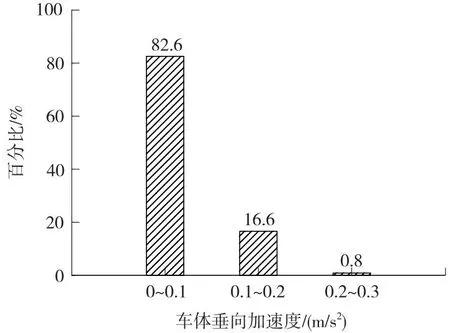
图7 车体垂向加速度频数分布Fig.7 Frequency distribution of the carbody vertical acceleration

由图7可知,车体垂向加速度在0～0.1,0.1～0.2,0.2～0.3 m/s2区间内的占比分别为82.6%、16.6%、0.8%,其中占比最大(82.6%)的区间为0～0.1 m/s2。

对所计算的车体横向加速度时程曲线进行统计,得到其在不同数值区间上的频数分布,见图8。

图8 车体横向加速度频数分布Fig.8 Frequency distribution of the carbody lateral acceleration

由图8可知,车体横向加速度在0～0.03,0.03～0.05,0.05～0.1 m/s2区间内的占比分别为78.8%、16.9%、4.3%,其中占比最大(78.8%)的区间为0～0.03 m/s2。

近年来，随着国内钾肥产业不断扩大，产量快速增加，提高国产钾肥市场份额、保障我国钾肥自给、提升中国在国际钾肥市场中的地位和进口谈判中的主动权，成为世界钾肥价格洼地。国产钾肥的发展，极大地减少了我国钾肥的对外依存度，为保障我国粮食安全做出了突出的贡献。

对所计算的前转向架一位电磁铁左右侧悬浮力时程曲线进行统计,得到其在不同数值区间上的频数分布,见图9。

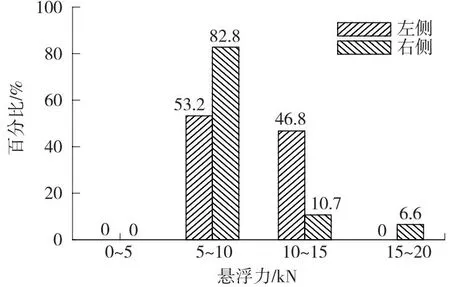
图9 悬浮力频数分布Fig.9 Frequency distribution of the levitation force

由图9可知,左侧悬浮力在0～5,5～10,10～15,15～20 kN区间内的占比分别为0%、53.2%、46.8%、0%,其中占比最大(53.2%)的区间为5～10 kN。同样,右侧悬浮力在0～5、5～10,10～15,15～20 kN区间内的占比分别为0%、82.8%、10.7%、6.6%,其中占比最大(82.8%)的区间为5～10 kN。

对所计算的前转向架一位电磁铁左右侧导向力时程曲线进行统计,得到其在不同数值区间上的频数分布,见图10。

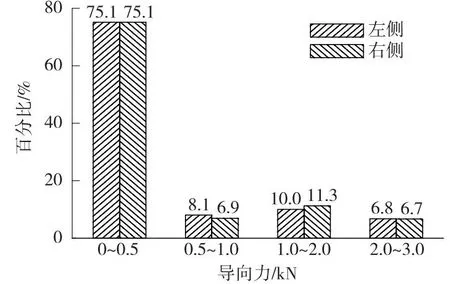
图10 导向力频数分布Fig.10 Frequency distribution of the guiding force

由图10可知,左侧导向力在0～0.5,0.5～1,1～2,2～3 kN区间内的占比分别为75.1%、8.1%、10%、6.8%,其中占比最大(75.1%)的区间为0～0.5 kN。右侧导向力在0～0.5,0.5～1,1～2,2～3 kN区间内的占比分别为75.1%、6.9%、11.3%、6.7%,其中占比最大(75.1%)的区间为0～0.5 kN。

由上述分析可知,各项动力学指标主要分布区间均在限值以下,满足行车平稳性要求。

(2)曲线半径影响分析

为了探究不同曲线半径对各项动力学指标的影响,计算不同圆曲线半径上车体垂向加速度、横向加速度、曲线内外侧悬浮力和导向力的最大值、平均值及有效值,计算结果见表4。

表4 各项动力性能指标统计值

由表4可知,圆曲线上各项指标的最大值、平均值和有效值均满足舒适性限值要求。以车体垂向加速度有效值为例,绘制其与曲线半径的关系(见图11)。

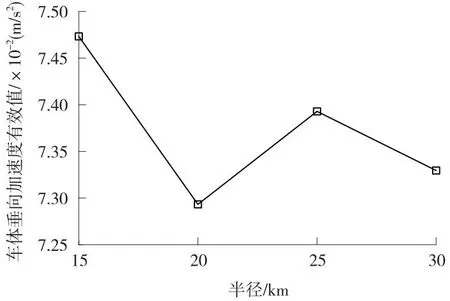
图11 车体垂向加速度随曲线半径变化关系Fig.11 Variation of vertical acceleration of the carbody against curve radius

由图11可知,曲线半径从15 000 m增加至30 000 m时,车体垂向加速度有效值呈现出先下降后上升再下降的趋势,但均远低于限值1.3 m/s2。车体垂向加速度有效值在曲线半径20 000 m处数值最小,这是由于曲线半径20 000 m、车速1 000 km/h与横坡为16°相匹配造成的。

以车体横向加速度有效值为例,绘制其与曲线半径的关系(见图12)。

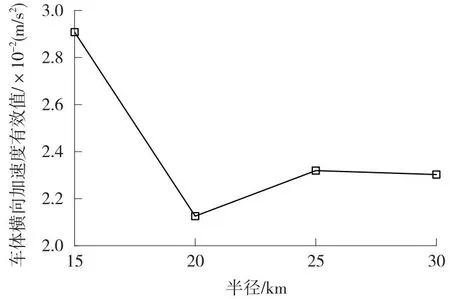
图12 车体横向加速度随曲线半径变化关系Fig.12 Variation of lateral acceleration of the carbody against curve radius

由图12可知,曲线半径从15 000 m增加至30 000 m时,车体横向加速度有效值呈现出先下降后上升再下降的趋势,但均远低于限值1.0 m/s2。车体横向加速度有效值在曲线半径20 000 m处数值最小,这是由于曲线半径20 000 m、车速1 000 km/h与横坡为16°相匹配造成的。以曲线内外侧悬浮力有效值为例,绘制其与曲线半径的关系曲线(见图13)。

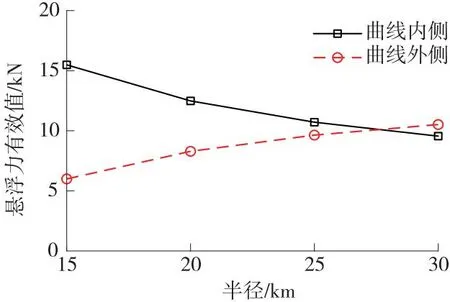
图13 悬浮力随曲线半径变化关系Fig.13 Variation of the levitation force against curve radius

由图13可知,曲线半径从15 000 m增加至30 000 m时,曲线内侧悬浮力逐渐下降,而曲线外侧悬浮力逐渐上升,且曲线半径增大到30 000 m时,曲线外侧悬浮力反超内侧悬浮力,这是因为半径30 000 m、横坡为16°时车辆处于过超高状态;同时,曲线内外侧悬浮力平均值始终处于10 kN左右。

以曲线内外侧导向力有效值为例,绘制其与曲线半径的关系(见图14)。

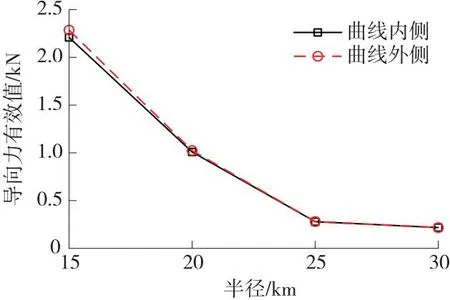
图14 导向力随曲线半径变化关系Fig.14 Variation of the guiding force against curve radius

由图14可知,曲线半径从15 000 m增加至30 000 m时,导向力整体处于下降趋势,这是由电磁铁与导轨间的变形差所决定的;同时,曲线内外侧导向力较为接近。

综上所述,随着曲线半径的增大,车体垂向和横向加速度先减小后增大再减小,但均远小于舒适性限值;曲线内侧悬浮力、导向力随曲线半径的增大而减小,曲线外侧悬浮力随曲线半径的增大而增大。横坡16°、车速1 000 km/h时,曲线半径20 000 m所对应车体振动加速度最小,该曲线半径下的车辆动力学性能较优。