吊杆无应力长度及竖直度控制技术研究

廖 硕

(中南勘察设计院集团有限公司 武汉 430061)

钢箱拱桥通过吊杆将桥面系与钢箱拱肋直接相连,主拱肋承担桥面系荷载,并产生水平推力,从而达到自平衡。吊杆作为中承式和下承式拱桥主要传力构件,在钢拱桥、钢管混凝土拱桥和混凝土拱桥中应用较为普遍[1]。由于钢箱拱桥是高次超静定结构,所使用的施工方法和施工程序对成桥状态下拱肋的线形及恒载内力有很大的关系[2]。在施工阶段中,随着结构体系和荷载的不断变化,整个结构的变形及内力也不断变化。钢箱拱桥吊杆的无应力长度是拱桥施工控制的一个重要参数。通常情况下吊杆锚具的富余长度(锚圈在锚杯上的调整长度)大于各种施工阶段因素引起的修正长度[3]。施工阶段因素对于吊杆的安装精度也会产生较大的影响,进而会对成桥阶段的运行产生影响。

目前,吊杆的无应力长度计算采用传统方法,针对于传统方法计算的无应力长度,在安装过程中会受到许多因素的影响导致吊杆的安装精度无法达到,对吊杆的竖直度也产生一定的影响。这将会直接影响成桥状态下桥面系的线性、吊杆的索力及成桥状态下的受力。

因此,本文针对影响吊杆无应力长度精确计算的因素及对吊杆竖直度的控制。拟提出应考虑修正的其他因素,并分析影响吊杆竖直度的相关原因。以工程实例为背景,建立有限元分析模型进行数据分析与对比,验证计算吊杆无应力长度时应考虑修正的其他因素的影响以及对吊杆竖直度的控制技术。

1 吊杆无应力长度及竖直度控制应考虑修正的因素

工程中,常根据传统吊杆无应力计算长度方法计算吊杆的下料长度供工厂制作及吊杆安装,但在实际安装过程中,吊杆的安装精度将受到施工阶段各种因素的影响,如吊杆制作与现场安装温度差异、钢箱拱肋的预拱度,预抬高、桥面系格子梁吊装节段预拱度及吊装位置、吊杆材料参数误差等。

1.1 温度差异

目前拱桥均采用成品吊杆,吊杆下料加工在室内完成,将温差定义为工厂室内制作时的温度与标准温度的绝对值差值,标准温度为现场吊杆安装时的环境温度。由于温差的存在,对吊杆无应力长度有一定的影响。温差对吊杆无应力长度的修正值按式(1)、式(2)进行计算。

平均线膨胀系数定义如下[4]。

(1)

式中:t1、t2为温度,℃,(t2>t1);L1为t1温度时的长度,m;L2为t2温度时的长度,m;L0为室温时的长度,m。

吊杆无应力长度修正值LX(m)定义如下。

LX=L0(t2-t1)α1

(2)

1.2 拱肋预拱度

拱肋在合龙之后将受压,在施工阶段应考虑设置预拱度,以保证其成桥线性。拱肋制造预拱度应综合考虑拱肋施工阶段累计变形及成桥预拱度因素。因此,拱肋预拱度的设置将改变吊杆原设计安装位置,进而使吊杆无应力下料长度与原计算的长度产生差别,对吊杆安装精度产生影响。

1.3 桥面系吊装及预拱度

桥面系在活载作用下主梁将产生挠度。 根据JTG D62-2004 《公路钢筋混凝土及预应力混凝土桥涵设计规范》[5]的相关规定,桥面系在相应施工阶段需要设置预拱度 ,预拱度的设置导致吊杆安装时的位置与原设计的位置存在几何偏差。桥面系吊杆横梁区分段在顺桥方向上不对称,见图1。因此,造成了两吊杆之间受力不一致,间接影响了吊杆安装精度及对吊杆竖直度的控制。

1.4 吊杆材料的非线性变化

吊杆的材料参数与JTG/T D65-06-2015 《公路钢管混凝土拱桥设计规范》[6]的标准值存在一定的误差。弹性模量误差对吊杆无应力长度有一定的影响。

吊杆安装完成后,随着桥面系吊装、桥面板安装等恒载的加入,其所受的拉力也会逐渐增加。由于吊杆所受拉力增加,相对于原长度必然有所伸长,而吊杆的体积是一定的,不会产生变化,因此其横截面积必然会变小。

2 依托工程

2.1 工程概况

该钢箱拱桥主桥采用计算跨径252 m中承式钢箱拱桥,主拱圈计算跨径为252 m,矢跨比为1/4.5,拱轴系数为m=1.3。拱肋为平行拱,拱肋中心间距28 m,吊杆区单侧距离2.4 m。拱肋采用变高度箱形截面,宽2.4 m、高3～5.5 m,采用单肋分幅转体施工,单侧拱肋划分为24个节段,拱肋节段在引桥支架进行拼装,拼装完成后通过平转+竖转相结合的方式进行转体并合龙。主桥总体布置见图2。

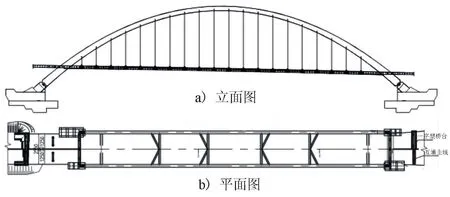
图2 主桥总体布置图

2.2 吊杆、桥面格子梁及安装顺序

主桥桥面系采用钢纵梁、钢横梁与混凝土桥面板及湿接缝形成的组合梁格体系。钢横梁分为吊杆横梁、次横梁、小横梁和拱间横梁4类。钢纵梁分为边纵梁与中纵梁2大类。桥面板采用C50混凝土,钢筋混凝土结构,分块预制。

吊杆布置见图3。采用GJ15-19B、12B型整束挤压成型钢绞线吊杆,纵向间距10 m,全桥共20对。吊杆上端采用张拉端锚具,上锚头采用球型支座和垫板锚固于拱肋横隔板支架上,吊杆长度的调整通过调节螺母位置来实现。吊杆下端采用固定端锚具,下锚头采用销接式,叉形耳板与横梁处耳板通过销轴连接,吊杆拱肋锚点构造见图4,吊杆主梁锚点一般构造见图5。

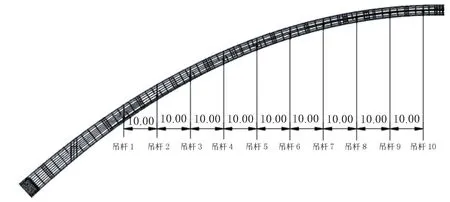
图3 吊杆立面布置(单位:m)

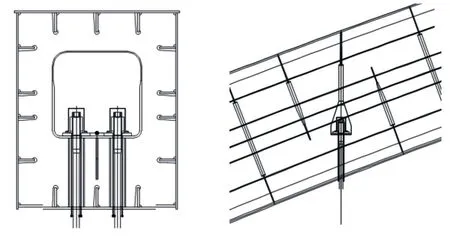
图4 吊杆拱肋锚点构造

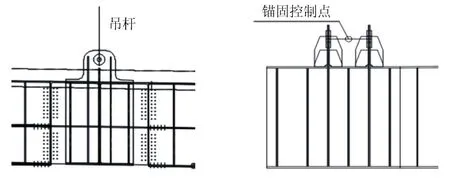
图5 吊杆主梁锚点一般构造

桥面系分无索区、吊杆横梁区及跨中嵌补区,共计25个吊装节段,采用对称吊装。各吊装段重量见表1。

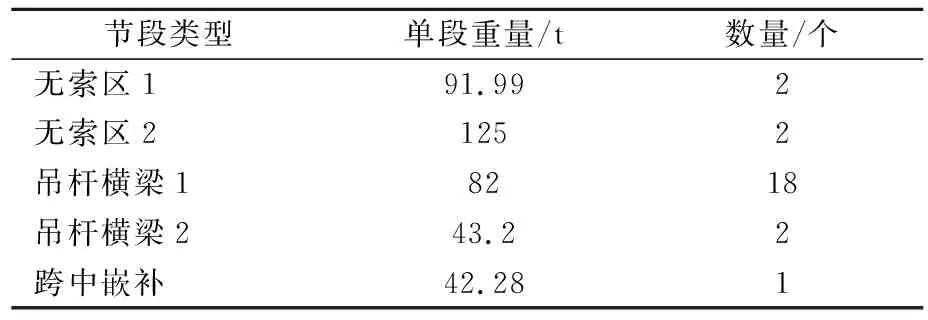
表1 桥面梁吊装节段重量统计

3 算例分析验证

3.1 有限元模型

采用midas Civil2021有限元软件建立施工阶段及成桥模型。除转体施工扣索,平衡索、吊杆采用桁架单元及桥面板采用板单元以外,其余部分均采用梁单元进行模拟。全桥共计1 847个节点,3 228个单元。对于施工阶段的全过程分析,一共定义了39个施工阶段。有限元计算模型见图6,计算参数见表2。

表2 各主要构件参数

图6 有限元计算模型

3.2 吊杆无应力长度计算

在实际工程中,根据吊杆的设计长度,加上有限元模型运行分析后吊杆受力产生的上下端位移差值计算吊杆受力后的长度,再通过查阅吊杆的相关材料参数即弹性模量、横截面面积,以及模型中吊杆内力计算得到吊杆伸长量,最后用吊杆受力后长度减去伸长量得到吊杆无应力长度[7-8],具体计算过程见式(3)～式(5)。

吊杆受力后的长度

l2=l0+uis-uix

(3)

吊杆伸长量

Δl=l2/(l+E·A/Fi)

(4)

吊杆无应力长度

l1=l2-Δl

(5)

式中:l0为吊杆设计长度,m;uis为第i施工阶段吊杆上端累计位移值,m;uix为第ix施工阶段吊杆下端累计位移值,m;Fi为第i施工阶段吊杆力,kN;E为吊杆弹性模量,GPa;A为吊杆截面面积,m2。

计算得出吊杆无应力长度见表3。

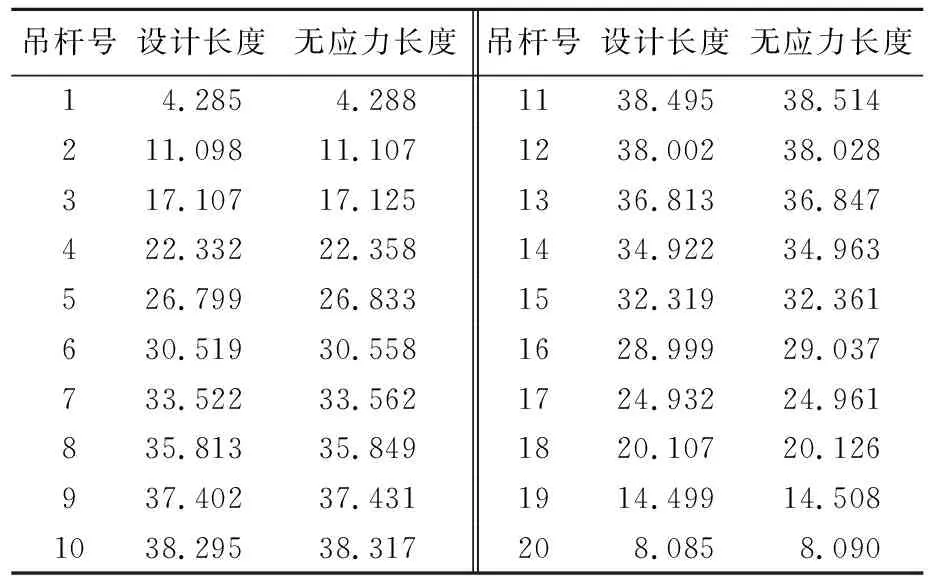
表3 吊杆无应力长度 m

3.3 环境温差影响分析

由式(1)、式(2)计算温差对吊杆无应力长度的修正值,本算例选取3个工况进行分析,分别对应环境温差10,20,30 ℃,分析不同温差下的吊杆无应力长度修正值,其曲线见图7。

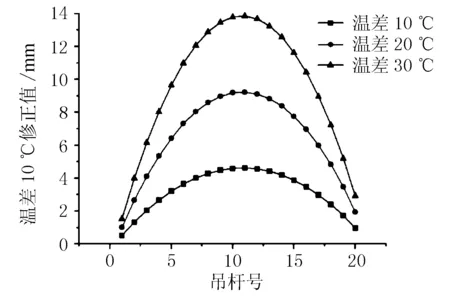
图7 不同温差工况下的吊杆无应力长度修正值

由图7可知,温差为10 ℃时,最大修正值4.620 mm,最小修正值为0.515 mm;温差为20 ℃时,最大修正值9.240 mm,最小修正值为1.030 mm;温差为30 ℃时,最大修正值13.860 mm,最小修正值为1.544 mm;温差每上升10 ℃,修正值增加4.620 mm。总体来看,不同温差对吊杆无应力长度均有一定的影响。温差对短吊杆的影响较小,对中长吊杆的影响较大。温差越大,对吊杆无应力长度影响较大。

因此,温差对吊杆安装精度有一定影响,在计算吊杆的无应力下料长度时应结合工厂环境及安装环境对吊杆长度进行修正,以满足安装精度的要求。

3.4 拱肋及桥面系预拱度影响分析

拱肋及桥面系制造预拱度综合考虑了拱肋施工阶段累计变形及成桥预拱度因素。按照传统方法计算吊杆无应力长度时,已经考虑了拱肋及桥面系施工阶段的累计变形,但是由于拱肋成桥预拱度与桥面系成桥预拱度的设置数据不同,将导致拱肋与桥面系对应位置的竖向位移产生差异。

按照本工程设计要求,拱肋设计成桥预拱度为跨中15 cm,桥面系设计成桥预拱度为跨中9 cm,其余各控制点均按二次抛物线插值得到。从有限元模型中提取拱肋吊杆对应点与桥面系吊杆对应点的施工阶段累计变形值。设计预拱度与施工阶段累计变形值相加得到拱肋与桥面系制造预拱度。并计算拱肋与桥面系制造预拱度的差值。拱肋及桥面系制造预拱度及差值曲线图见图8。

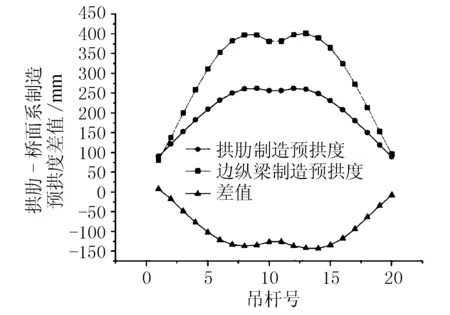
图8 拱肋-桥面系制造预拱度比较

由图8可知,拱肋的制造预拱度普遍大于桥面系的预拱度,这是由于施工阶段累计变形的差异及成桥设计预拱度设置不同导致的。两者最大差值为141.623 mm,最小差值为7.765 mm。

拱肋及桥面系制造预拱度的差异,不会影响吊杆的安装精度,但是对成桥状态有一定的影响。因此,吊杆长度的确定,除按无应力长度确定之外,还需考虑最终的成桥目标: ①成桥桥面线形满足要求;②吊杆索力满足要求且平顺;③成桥受力满足要求且平顺。

3.5 吊杆竖直度分析

通过对模型运行分析,查阅吊杆下端位移发现,吊杆在顺桥方向产生不同程度的位移值。因此本文提取了桥面系吊装完成后顺桥向位移值X1及成桥阶段的吊杆下端顺桥向位移X2,并对2个阶段的位移进行差值得到ΔX,曲线见图9。

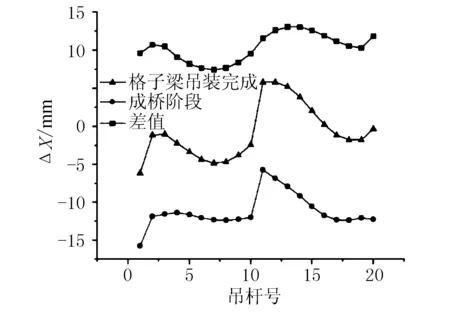
图9 吊杆下端顺桥向位移比较

由图9可知,桥面系吊装完成后,吊杆下端产生了顺桥向位移,最大位移值为-6.144 mm,最小位移值为0.222 mm。在成桥阶段,最大位移值为-15.76 mm,最小位移值为-5.728 mm。成桥阶段因受到车辆荷载等因素的影响,其顺桥向位移值普遍大于桥面系吊装完成后的位移值,2个阶段顺桥向位移的趋势大致相同,差值控制在7～13 mm。

由于吊杆下端在顺桥向产生了位移,吊杆安装完成后相比于设计状态,其竖直度会产生影响,通过有限元模型得出吊杆不同阶段变形云图见图10、图11。根据三角函数原理,计算得出成桥阶段各吊杆的倾斜角度θ的正切值,曲线见图12。

图10 桥面系吊装完成后吊杆顺桥向变形图

图11 成桥阶段吊杆顺桥向变形图

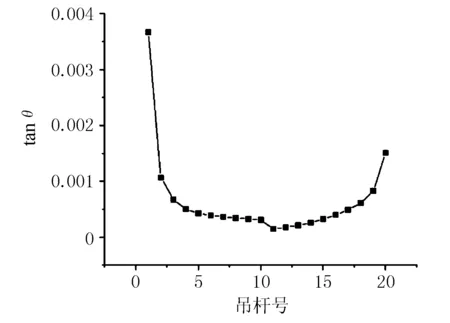
图12 成桥阶段吊杆倾斜角度θ正切值曲线

由图12可知,短吊杆倾斜角度较大,直接影响到短吊杆的长度。随着吊杆长度逐渐增大,吊杆倾斜角度越来越小。本文取该工程30 m以下的吊杆,结合吊杆竖直度及产生的顺桥向位移,分析比较了吊杆倾斜前后的长度对比见图13,吊杆长度变化差值见图14。

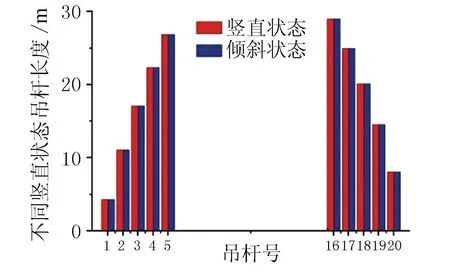
图13 短吊杆倾斜前后长度对比

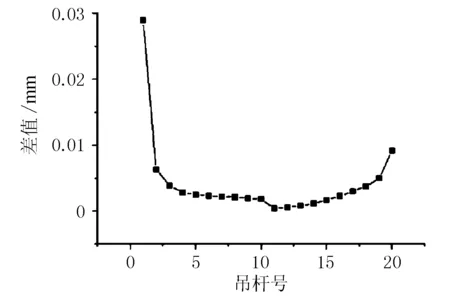
图14 吊杆长度变化差值

由图13、图14可知,30 m以下对吊杆竖直度有一定的影响,吊杆1为全桥长度最短的吊杆,其长度变化也是相对最明显的,倾斜前后长度差值为0.028 mm。由于此算例计算跨径较小,吊杆的倾斜程度相对来说不明显。但对于大跨度的钢箱拱桥来说,对吊杆竖直度的控制尤为关键。

综上,吊杆下端产生顺桥向位移导致对吊杆竖直度产生影响,在桥面系吊装完成后出现顺桥向位移主要有以下几方面原因:①吊装节段的划分本身在顺桥向不对称,导致吊杆张拉时两端受到的荷载不同;②桥面系由于设置了预拱度,其本身存在一定倾斜,导致安装完成后吊杆产生了顺桥向的位移;③成桥阶段此位移变大主要是由于活载等因素引起。

3.6 吊杆材料非线性变化的误差分析

弹性模量的非线性变化[9]对吊杆无应力长度的计算有一定的影响,因此,无应力长度计算时应考虑吊杆弹性模量误差引起的影响。本算例弹性模量增大比例取1.5%,求得吊杆无应力长度变化见图15。

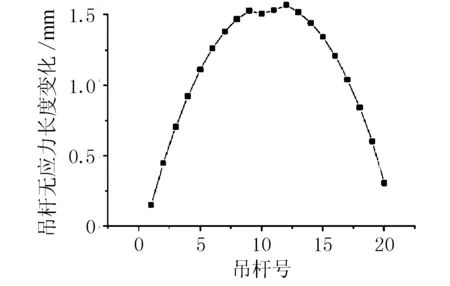
图15 吊杆材料参数对无应力长度影响

由图15可见,随着吊杆长度的增加,考虑弹性模量误差修正值逐渐增大,最大变化值为1.535 mm,最小变化值为0.153 mm。吊杆材料弹性模量误差对吊杆无应力长度有一定的影响,在计算吊杆无应力长度时应考虑弹性模量误差的影响。

在实际钢箱拱桥工程中,吊杆横截面面积随着受力变化而变化,由几何关系可知

式中:V为吊杆体积,m3;L为吊杆总长度,m。吊杆随着桥面系荷载的逐渐增加,所受拉力逐渐增大,必然导致L逐渐增大,但V不变,因此A会逐渐变小。故吊杆受力后横截面积的变化也会对吊杆无应力长度造成影响。

4 结语

本文针对钢箱拱桥吊杆无应力长度进行研究,分析了目前吊杆无应力长度算法的精确性及对吊杆安装精度的影响,提出对吊杆无应力长度精确计算应考虑的修正因素。并以实际工程为背景,验证吊杆制作及安装时的温度差异、拱肋及桥面系的几何偏差、吊杆材料参数误差对吊杆长度的影响。通过有限元模型数据研究吊杆顺桥向位移对吊杆竖直度及长度的影响,总结了影响吊杆竖直度的因素。