基于监测数据的基坑工程安全评判

赵 剑，李双艳，徐剑敏，刘定邦，赵 磊

（1.深圳地质建设工程公司，广东 深圳 518000；2.中南林业科技大学，湖南 长沙 410000；3.深圳市地铁集团有限公司，广东 深圳 518000）

0 引 言

基坑工程是一个拥有悠久历史、具有重大意义的研究方向，具有里程碑式的价值。它要求解决土力学中的结构稳定、变形控制、渗漏控制等技术难题，确保基坑和周围环境的安全。21世纪之后，随着我国城市建设的高速发展，有限的地上空间已不能满足人类的建设需求，需向地下寻求更大的建设空间，从而大量的深基坑工程随之产生。然而，由于深基坑工程大多数都是临时施工，安全保障措施的缺乏，使得这些工程的风险极高，事故频发[1-2]。因此，对基坑工程进行安全风险评估十分必要。然而，风险本身是具有一定的不确定性及模糊性，需要采用科学的方法对其进行评价。

EINSTEIN[3]早在20世纪70年代便开始探索并运用风险管理的概念，深入剖析了地铁工程的风险控制，并提出了一系列具有实践意义的建议。张飞燕等[4]采用CIM-AHP 模型和组合赋权技术，可以有效地评估地铁施工中的安全风险，这种技术既可以将定量分析与定性分析相结合，又可以将客观因素与主观因素有机结合，大大提升了安全风险评估的准确性和可靠性。申建红等[5]通过应用D-S证据理论，建立了一个深基坑施工风险评估模型，以便更好地评估深基坑施工的风险因素。李朝阳等[6]应用三级模糊综合评判计算模型对地铁车站基坑施工风险进行评估。

基坑工程处于复杂的地下水和应力环境中，基坑工程的复杂性不仅体现在其结构特征和影响因素上，而且还受到土体、受力状况以及运营环境等多种因素的影响，从而使得它们的复杂性大大增加。很明显，对于基坑工程的安全性进行评估存在着巨大的不确定性，既可能存在随机因素，也可能存在模糊因素。模糊综合评判法是一种新的数学方法，它可以帮助我们更好地识别多目标决策中的复杂因素，特别是在面对模糊性较强的情况下，更能发挥出它的优势[7]。安全性是基坑工程的关键，它体现在基坑围护体系和周边环境的安全。通过监测数据，可以清楚地看到基坑围护体系和周边环境的变化[8]，从而确保基坑工程的安全运行。本文通过综合运用层次分析法与模糊综合评判法，构建了一个以实时监测数据为依托的基坑安全评估模型。

1 基坑安全评判流程

基于监测数据的AHP（Analytic Hierarchy Process）-模糊综合评判法的深基坑施工安全评估应用时，归纳起来主要有以下几个步骤。

首先，建立一个评估指标体系，使用层次分析法（AHP）和工程经验来比较不同层次的要素。然后，根据一定的标度理论，得出它们的相对重要程度[9]。

其次，根据工程实际情况，划分基坑工程安全等级，建立基坑工程安全评语集。

最后，建立合理的隶属函数，根据隶属函数建立模糊综合评判矩阵。逐级进行模糊综合评判，最后求得基坑工程整体所处的安全等级。

2 层次分析法指标权重确定

2.1 评价指标的选取

根据基坑设计深度、地质特征、外部环境条件、支撑结构类型、施工技术要求等多方面因素，应当对基坑工程进行全面的监测，以确保安全可靠的施工。本文根据《建筑基坑工程监测技术标准》（GB 50497—2019）[10]对监测内容的要求，选取其中的应测项作为评价指标的选取范围。在实际工程中，应根据设计施工图纸的要求，对监测项目进行取舍。

2.2 评价指标权重确定

层次分析法的基本步骤如图1所示。在本文中，省略了对层次总排序的一致性检验过程。

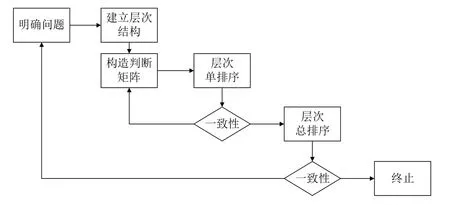
图1 层次分析法的基本步骤Fig.1 Steps of AHP

采用层次分析法，可以将决策判断转换成可衡量的数据，并以1～9的比例来衡量每个评估指标的重要性，以此来实现数据的可视化表达。本文通过行业内专家调查结合多年工作经验给各评价指标予以赋值。

（1）构造层次分析结构

以基坑监测中9个最常见的监测项目（围护结构顶水平位移和竖向位移、测斜、立柱沉降、支撑轴力、地下水位、周边建筑物沉降、管线沉降、周边道路沉降）为例，介绍评价体系的建立过程，深基坑施工安全评价指标体系如图2所示。

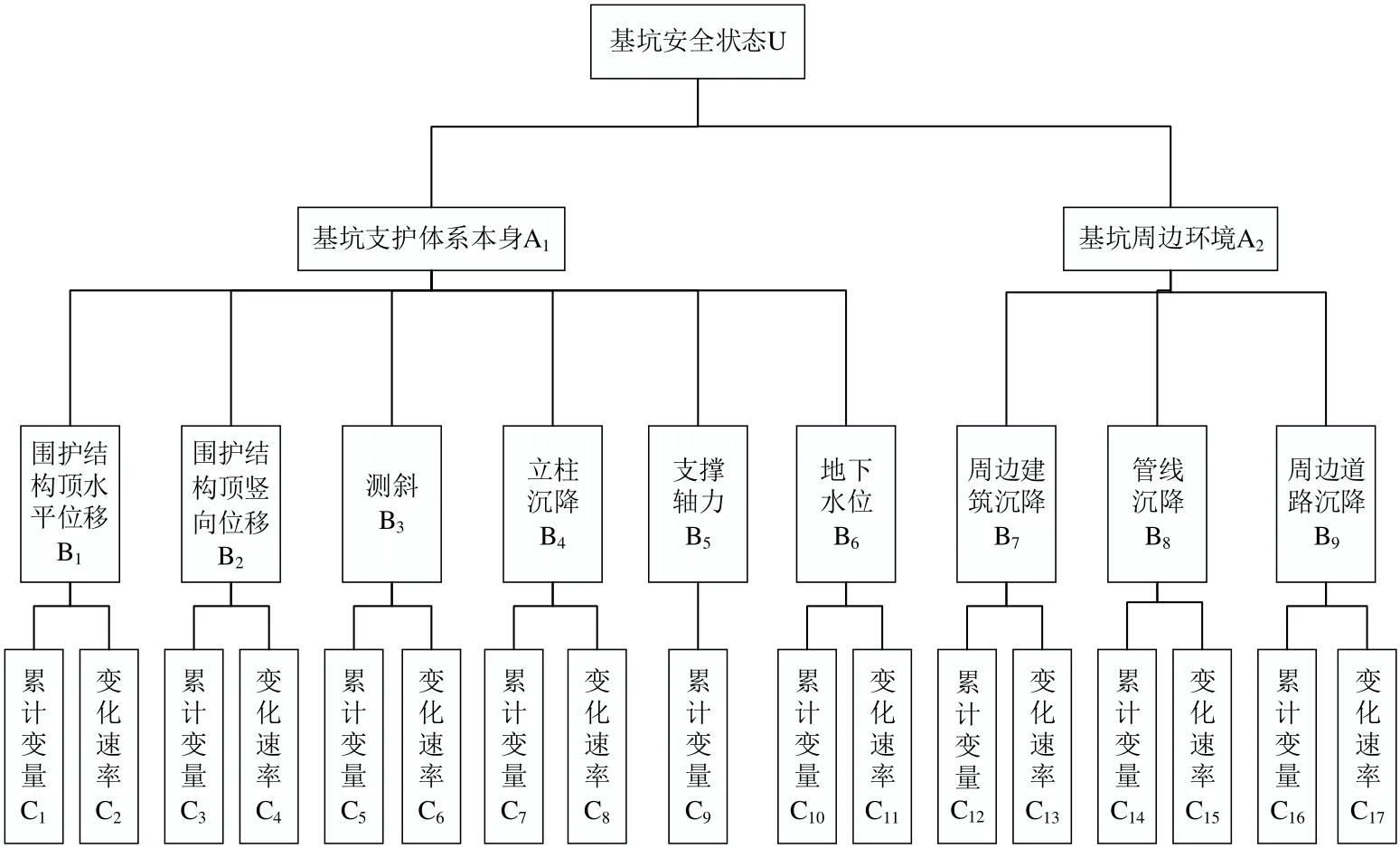
图2 深基坑施工安全评价指标体系Fig.2 Safety evaluation index system for deep foundation pit construction

（2）构造判断矩阵

a）第一层评价指标

在第一层评价指标中，基坑支护体系本身的变形大小是基坑工程是否安全的最直接体现，而周边环境的变形除了受基坑施工的影响，还可能受外界条件的影响，诸如周边建（构）筑物的结构形式、行走车辆等。因此，基坑支护体系本身的重要性相比周边环境更为重要，因此建立如表1所示的深基坑工程施工安全判断矩阵。

表1 深基坑工程施工安全判断矩阵Table 1 Safety judgment matrix of deep foundation pit construction

b）第二层评价指标

对于基坑支护体系本身而言，基坑变形的最直观表现为围护结构顶部水平位移，其次为深层水平位移。在支护体系发生水平位移的同时，支撑轴力也会随之变化，因此两者具有相同的重要性。随着支护结构水平位移的发生，周边土体应力随之发生变化，从而导致围护墙顶部竖向位移、立柱沉降、地下水位等监测项目随之产生变形。

对于基坑周边环境而言，周边建筑物由于其自身基础的存在，因此周边建筑物沉降的重要性程度不如周边道路竖向位移。而周边管线的监测受环境及现实因素的影响，几乎所有的管线监测只能采取间接法，因此周边管线竖向位移重要性在周边环境的指标中最低。根据以上分析结果，构造第二层指标的判断矩阵，结果如表2～3所示。

表2 基坑周边环境判断矩阵Table 2 Judgment matrix of surrounding environment of foundation pit

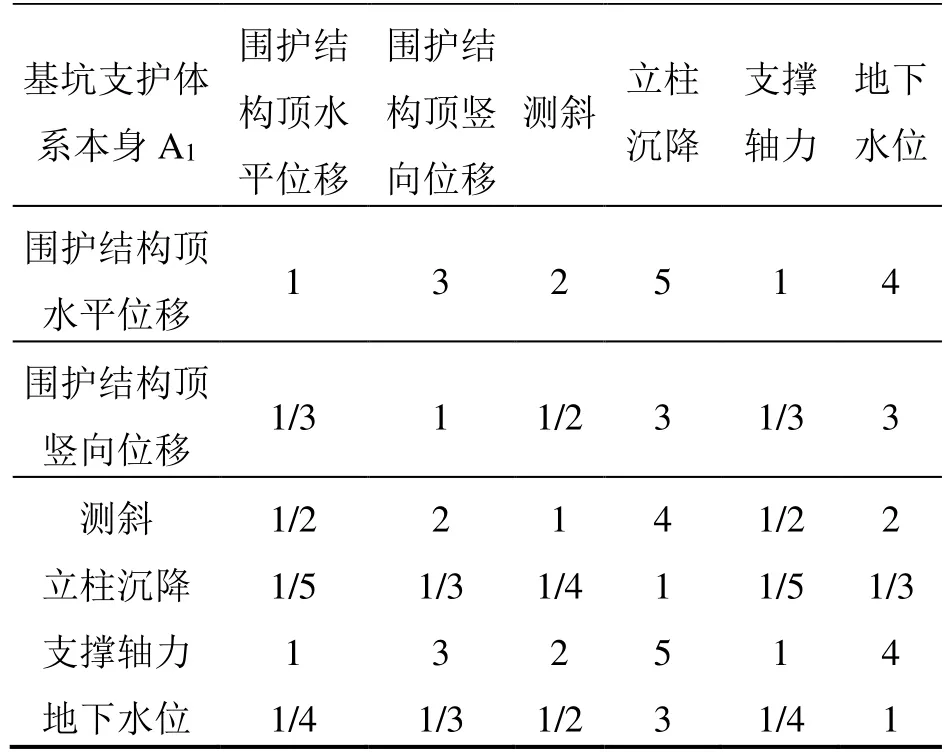
表3 基坑支护体系本身判断矩阵Table 3 Judgment matrix of foundation pit support system

c）第三层评价指标

除了支撑轴力外，第三层评价指标均含有累计变化量和变化速率两个指标。在实际工作中，当累计变化量达到设计控制指标时，须立即予以报警，停止现场施工，对报警位置进行现场调查分析；而对变化速率，一般取连续三天的变化速率判别基坑是否需要报警。因此，累计变化量较变化速率相对更加重要，因此建立如表4所示的判断矩阵。

表4 判断矩阵Table 4 Judgment matrix

（3）通过建立多个指标的判断矩阵，可以更准确地评估每个指标的重要性，但是，为了避免这些判断之间出现矛盾，还需要进行一致性检验，以确保它们的准确性。引入判断矩阵最大特征根以外的其余特征根负平均值作为评定一致性指标，即：

当CI值较大时，表明矩阵与预期的一致性存在较大差异；而当CI值较小时，则表明矩阵的一致性较高。为了确定矩阵的一致性，还须考虑它的平均随机一致性指标RI。1～9阶判断矩阵的RI值见表5。

表5 平均随机一致性指标Table 5 Average random consistency index

当矩阵的阶数超过2时，我们可以通过计算CI和RI的比值来评估它们的一致性，这个比值被称为CR，CR=CI/RI，也就是所谓的随机一致性比率。如果CR小于0.10，则可以确定该矩阵具备良好的一致性。

3 基于模糊综合评判的深基坑施工安全评判

模糊综合评判是以模糊数学为基础，通过将待研究的模糊实体和它们所代表的模糊概念组合成一个模糊集合，并利用相应的隶属函数，结合模糊集合的相关运算和变换，可以实现对模糊实体的定量分析。

3.1 确定评价集

为了确保基坑的安全，施工期间必须建立有效的监测机制，以便及时发现、报告并进行有效的管理。这些机制的设定需要考虑到监测项目的累积变化量及其变化的速度。监测警戒值是指根据设计单位提出的指标控制值，对监测数据超过一定阈值的预警。根据土质特性、设计要求和当地实践经验，应当精确地确定监测控制值。

本文根据各监测项目实际量测值与监测指标控制值的比值，将基坑安全等级分为五级：Ⅰ级安全状态、Ⅱ级预警状态、Ⅲ级报警状态、Ⅳ级控制状态、Ⅴ级危险状态，从而建立基坑安全评语集：

V={v1，v2，v3，v4，v5}={Ⅰ级安全，Ⅱ级预警，Ⅲ级报警，Ⅳ级控制，Ⅴ级危险}

基坑安全等级划分如表6所示。

表6 基坑安全等级划分表Table 6 Safety classification of foundation pit

3.2 隶属函数的确定

根据数据判断特性，本文采用梯形分布函数。假设所有单因素的隶属函数都是相同的，并且都遵循线性分布，从而计算出基坑不同安全状态的隶属函数[8]。

（1）基坑处于安全状态的隶属函数

（2）基坑处于预警状态的隶属函数

（3）基坑处于报警状态的隶属函数

（4）基坑处于控制状态的隶属函数

（5）基坑处于危险状态的隶属函数

式中：x为各单因素的实测最大值；μ1、μ2、μ3、μ4、μ5分别对应基坑处于安全状态、预警状态、报警状态、控制状态、危险状态的隶属函数；x1、x2、x3、x4分别对应基坑处于预警状态、报警状态、控制状态、危险状态的指标预警值。

4 案例分析

4.1 工程概况

拟建桂湾四单元九年一贯制学校项目位于前海合作区桂湾片区，用地面积约3.71万m2，总建筑面积约9.5万m2，地上7层，地下2层（含半地下室）。场地北侧邻近创新九街，南侧邻近桂湾二路，西侧邻近创新六街，东侧为创新八街及高架桥。基坑开挖底标高为0.4～5.2 m，开挖深度5.3～11.4 m，开挖周长约900 m，开挖面积约为3.4万m2。

4.2 监测内容及控制指标

根据设计图纸，本项目监测内容及控制指标分别如表7～8所示。

表7 监测内容Table 7 Monitoring contents

表8 监测控制指标Table 8 Monitoring and control indicators

4.3 监测预警事件

2022年12月28日，围护结构顶部水平位移监测点 ZDW15、ZDW16累计变量分别达到−34.10 mm、−32.00mm，均超过设计预警值，第三方监测单位发出预警通知单。在预警点位附近，还布设有围护结构顶部竖向位移监测点（ZDC15、ZDC16）、地下水位监测点（SW7～SW9）、管线变形监测点（GX15～GX18）、周边地表竖向位移监测点（DL20～DL23）、支护桩深层水平位移监测点（CX6、CX7）。附近其它各项监测点的当天变化速率较之前亦有所增加，但仍处于设计允许范围内。根据2022年12月28日实测数据，取各类监测项目中的最大值，具体数值见表9。依据第3.2节中的隶属函数，建立模糊判断矩阵，判定基坑的安全性。

表9 基坑监测成果统计表Table 9 Statistics of foundation pit monitoring results

4.4 指标权重的确定

本项目建立如图3的基坑安全评价指标体系。

图3 基坑安全评价指标体系Fig.3 Index system for safety evaluation of foundation pit

（1）构造第一层判断矩阵，如表10所示，一致性检验结果附后。

表10 判断矩阵U-ATable 10 Judgment matrix U-A

（2）构造第二层判断矩阵，如表11～12所示，一致性检验结果附后。

表11 判断矩阵A1-BTable 11 Judgment matrix A1-B

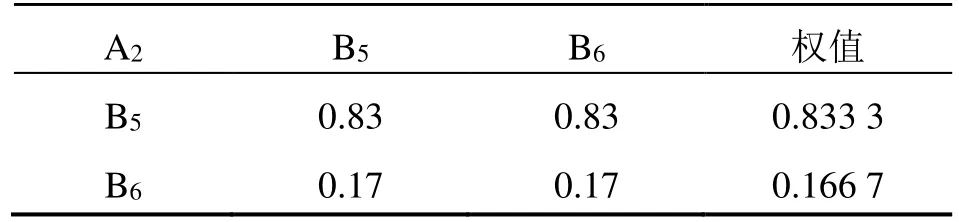
表12 判断矩阵A2-BTable 12 Judgment matrix A2-B

（3）第三层各因素具有相同的判断矩阵，构建的判断矩阵如表13所示。

表13 判断矩阵B-CTable 13 Judgment matrix B-C

（4）根据上述的层次单排序结果，可求得评价指标层次总排序结果，见表14。

表14 评价指标层次总排序Table 14 Overall ranking of evaluation index levels

4.5 基坑安全判定

（1）第三层模糊综合评判

第三层各因素评判矩阵：

根据4.4节所确定的第三层因素权重，得出第三层综合评判：

（2）第二层模糊综合评判

第二层各因素评判矩阵：

根据4.4节所确定的第二层因素权重，得出第二层综合评判：

（3）第一层模糊综合评判

第一层各因素评判矩阵：

根据4.4节所确定的第一层因素权重，得出第一层综合评判：

根据最大隶属度原则，说明该基坑处于Ⅰ级安全。基坑处于该安全等级时，建设单位、施工单位、监理单位、第三方监测单位等相关监控单位在信息报送的同时，应加强监测、巡视，同时根据当地相关文件要求，组织专家论证会，请专家对基坑的安全性给出最终结论及处理意见。

2022年12月30日，建设单位组织召开了《桂湾四单元九年一贯制学校——桩顶水平位移预警》会议，与会专家详细了解了基坑施工及监测情况。根据与会专家咨询意见，综合判断目前基坑整体处于安全稳定状态，建议根据基坑开挖实际情况，设计单位适当调整桩顶水平位移监测预警值。

5 结 论

（1）基坑工程安全事故的发生在前期一般都会有一定的征兆，如支护结构变形或支撑内力急剧增加等，但这些在初期是无法肉眼可见的。因此本文基于实际监测数据建立基坑安全评价指标体系，合理构建动态安全评估模型，得到基坑工程在各时间段安全状态的变化。

（2）在基坑施工安全判定过程中，利用基坑各监测项目的实际监测数据进行计算，可以有效避免对基坑安全评估的主观性，大大增加了基坑安全判定的客观性及合理性。

（3）基坑工程处于复杂的地下水和应力环境中，基坑工程的复杂性不仅体现在组成结构及影响因素方面，还体现在各因素的影响程度因不同的土体、受力状态和运营环境而有所不同。显然，基坑工程的安全性分析是不确定性问题，不仅具有随机性，也具有模糊性。