基于D-S证据融合理论的轨道电路补偿电容故障判决方法研究

罗依梦，许庆阳，段贺辉，徐永波，王泽宇

作为保证轨道电路正常传输的重要设备，补偿电容通常等间隔地安装于轨旁［1］，处于室外工作环境下，不可避免地会由于气温变化、异物击打、施工作业及自身老化等因素发生故障，导致失去对轨道电路传输的补偿作用，严重时可能会造成轨道电路“红光带”，影响行车效率。

目前，高速综合检测列车每月2次对高速线路轨旁信号设备执行动态检测，所采集的补偿电容脉冲数据及轨道电路感应电压数据均可反映补偿电容的工作状态。而补偿电容故障识别一直是信号领域研究的热门项点之一，如罗泽霖等［2］提出了一种基于WPD-CNN的补偿电容器故障诊断方法，从动态检测中提取补偿电容器的特性，并对其进行故障诊断；许庆阳等［3］提出了一种基于小波变换的补偿电容故障自动识别方法，可以有效识别补偿电容处的脉冲信号，并识别补偿电容的故障位置；王钟锐等［4］总结了3类以轨道检测车采集与集中监测系统为数据源的轨道电路故障诊断方法；洪玲等［5］提出了一种利用小波包分析方法来分析无接头轨道电路中补偿电容的故障特性；李亚兰等［6］使用EMD方法进行故障诊断，并提出了一种用于轨道电路系统故障检测和诊断的综合方法；王少迪等［7］提出了一种基于检测车数据的轨道电感回归估计方法，分析了补偿电容、轨阻抗和镇流器电阻对反馈信号幅值包络的影响；冯栋等［8］分析了补偿电容不同容值对补偿电容感应电压的影响，实现了电容的在线估算。虽然以上研究方法各异，但均是针对单一数据进行分析，在数据采集受到干扰导致数据质量不佳时，判决结果准确度容易受到影响。为此，本文提出利用D-S证据融合理论的方法，针对动态检测获取的数据进行多源分析，在单一判决结果的基础上进行融合诊断，以提高补偿电容故障识别的准确性。

1 补偿电容动态检测数据

动态检测设备采集的补偿电容、感应电压动态检测数据见图1。当检测车运行至轨道电路补偿电容位置处，由车辆轮对、钢轨以及补偿电容构成的电磁回路磁场强度会发生变化，由此形成补偿电容脉冲数据。当补偿电容处于故障状态时，相应位置的脉冲会下降或消失，见图1（a）；受钢轨的感抗作用，无绝缘轨道电路的高频信号从发送端到接收端应呈递减趋势，沿线加装的补偿电容起到了抵消感抗的作用，因此感应电压呈现波动式衰减。当某个补偿电容失效时，相应位置感应电压会产生变形，见图1（b）［9］，C16为发送端，C1为接收端。

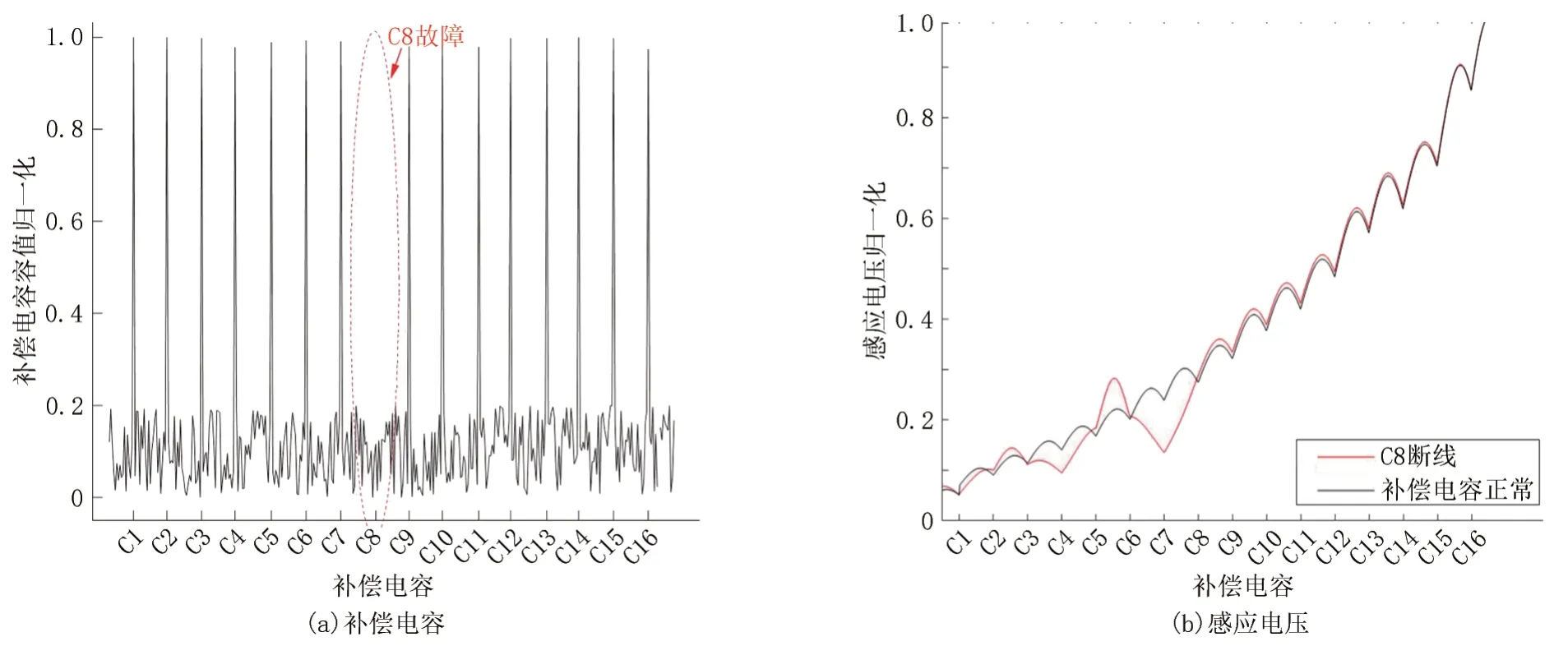
图1 信号系统动态检测数据

2 基于D-S证据融合理论的补偿电容故障判决方法

基于D-S（Dempster-Shater）证据融合理论的补偿电容故障判决方法主要步骤包括：基于补偿电容脉冲的故障识别、基于感应电压数据的故障识别，以及基于D-S证据融合理论的故障判决3部分，见图2。分别从补偿电容脉冲曲线及感应电压曲线中提取补偿电容状态特征，在单一判决结果的基础上进行融合诊断，最终输出多源分析后的补偿电容故障判决结果。

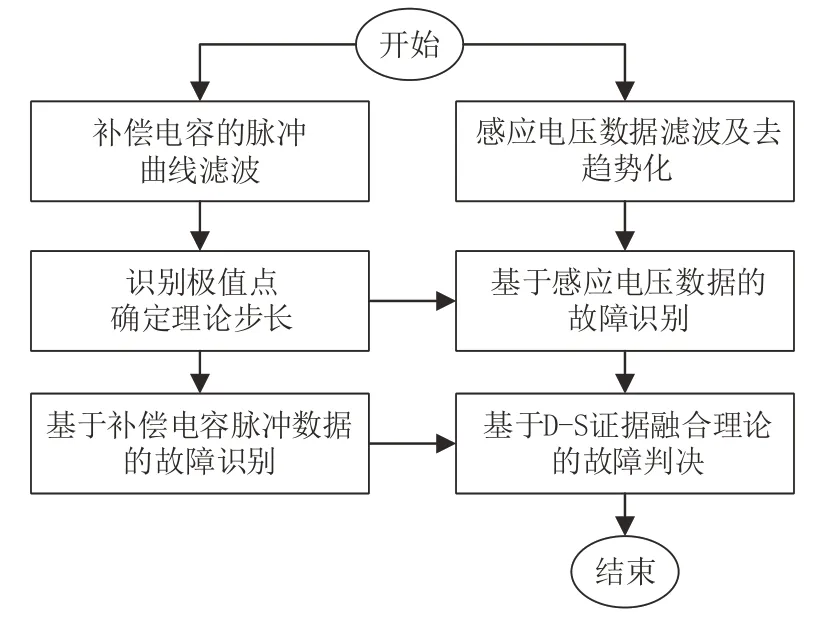
图2 基于D-S的补偿电容故障判决方法

2.1 基于补偿电容脉冲的故障识别

由于补偿电容工作环境复杂，检测数据中存在杂波、基线漂移等问题，所以首先需要对补偿电容脉冲数据进行滤波及归一化处理，提取主轨道范围内数据，进而通过阈值判断补偿电容是否存在故障。除此以外，为保证基于感应电压数据的故障识别准确性，还需要识别补偿电容脉冲极值点，获取理论步长，以确认补偿电容位置。步骤如下。

Step 1对补偿电容脉冲数据进行滤波及归一化处理。

Step 2识别脉冲极值点作为补偿电容位置，根据区段补偿电容个数确定理论步长，并对识别到的补偿电容位置进行修正。若在理论步长附近没有找到极值点，则认为该位置的补偿电容存在故障；若在理论步长范围内出现多个极值点，则选取与理论步长最接近的点作为该位置的补偿电容，删除多余极值点。

Step 3以本区段补偿电容位置脉冲峰值均值的0.5倍作为判别条件，当任意补偿电容位置脉冲不满足以上条件时，认为补偿电容发生故障。根据脉冲信号判别结果见图3。

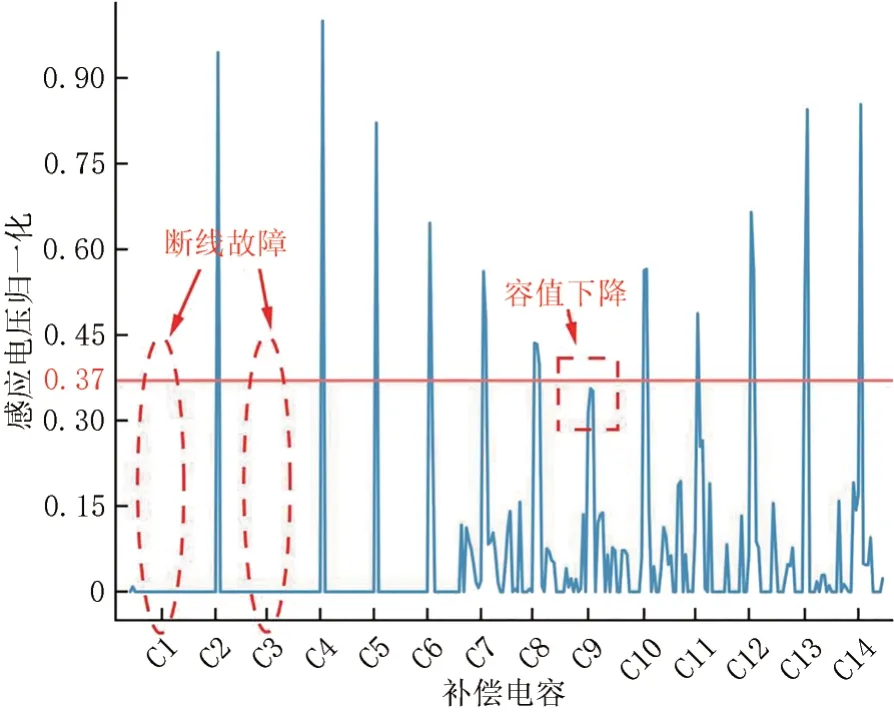
图3 根据脉冲信号判别结果

2.2 基于感应电压数据的故障识别

由于检测数据采集过程中存在干扰信号，为了通过感应电压数据进行补偿电容故障识别，首先需要对感应电压数据进行预处理，提取包含补偿电容信息的主轨道电路数据范围；然后进行滤波及去趋势化处理，获取如图4所示的感应电压波动特征；再通过识别极值点来判断补偿电容故障。步骤如下。

图4 感应电压数据波动特征

Step 1根据区段基本信息确定入口电流、出口电流位置，对调谐区范围数据进行切割，保留主轨道范围内的数据。

Step 2归一化和去趋势化处理。轨道电路感应电压从发送端到接收端呈波动递减趋势，其中每个波动极大值点对应补偿电容位置。由于对原始曲线进行判别较为复杂，故可利用加法模型［10］对曲线进行去趋势化处理，仅保留曲线波动特征，以此来简化判别运算。

Step 3对Step 2得到的感应电压曲线采取3次滑动均值滤波处理。分别选用一个较大的滑动窗口w1、较小的滑动窗口w2，对去趋势化的感应电压信号进行滤波；将2次滤波结果进行差分处理，随后选用更小的滑动窗口w3进行滑动均值滤波，使曲线更加平滑。

Step 4将Step 3得到的信号取反，并识别极值点，根据理论步长确定的补偿电容索引位置作校验，提取特征值，判别补偿电容是否存在故障。

2.3 基于D-S证据融合理论的故障判决

D-S证据融合理论最早于1967年，由A.P.Dempster和G.Shater提出，是一种处理不确定性问题的完整理论［11］，其核心是将多个主体相融合，以达到模式识别结果高于单个主体识别结果的目的，即将命题的不确定性转化为集合的不确定性。

设全域X为将要判断事件发生情况的范围，也称作识别框架或假设空间，其包含空集在内的所有可能情况［12］。D-S证据融合理论为每一个主体分配了基本概率，每一个主体对于全域X内所有的假设概率之和均为1。基本概率分配函数应满足

式中：函数m为基于统计证据获得的mass函数，即针对识别框架中的每一个假设分配的概率；A为全域X中的假设，故A在全域X内经过mass函数分配的概率结果之和为1；∅表示空集，则∅经过mass函数分配的概率结果为零。

某个假设的信度函数Bel为该假设所有的子集概率之和，即

式中：B为假设A的子集。

同时，与该假设交集不为空的概率之和，称为似然函数Pl（A），即

对于假设A，由信任函数与似然函数组成的闭区间［Bel（A），Pl（A）］，即为假设A的信任区间，表示对假设A的确认程度。

对于∀A⊆X，X上的2个函数m1、m2的D-S合成规则为

式中：K为D-S合成规则中的一个常数，用于归一化合成结果；B、C为所有两两相交结果为A的假设；m1为对B假设计算的mass函数，m2为对C假设计算的mass函数，m1⊕m2即为对假设A进行的D-S合成。

对于假设A合成的基本概率分配函数，即考虑所有两两相交结果为A的假设B、C，分别对B、C进行mass计算后的结果相乘，并将所有乘积进行累加，最终除以一个归一化系数K。K的数学表达式为

在D-S证据融合理论中，需满足证据间的独立性。因证据间的关联特性易导致结果的超估计，若多个证据之间存在冲突性，则融合结果易产生悖论。只有当证据之间互相独立、互不相关，才能保证融合结果的可靠性。补偿电容脉冲数据与感应电压数据由不同采集系统获取，相互独立，因此满足D-S数据融合的先决条件。

根据D-S证据融合理论以及本文的研究对象，为获取基本概率分配函数、信度函数和似然函数，需引入式（6）的钟型隶属度函数［13］。

式中：a、b为影响钟型隶属度函数曲线变化的参数；c是隶属度函数的中心，即钟型曲线的峰值所在的位置。补偿电容的脉冲极值点越小，感应电压波动特征的极值点越接近0，这意味着补偿电容出现故障的概率增大。

在本项研究中，设定参数a=0.3，b=6，c=0。对于补偿电容脉冲数据，定义θ为单个补偿电容脉冲的极值点与同一区段其他极值点均值的比值；对于感应电压数据，定义θ为单个补偿电容感应电压极值点与同一区段最大感应电压的比值。D-S证据融合理论的故障判决步骤如下。

Step 1应用基于补偿电容检测脉冲的故障识别方法和基于感应电压数据的故障识别方法，分别得到各自的分类依据。

Step 2根据式（6），计算出2种方法对每个假设的支持度，也就是每个补偿电容的故障概率。

Step 3采用D-S证据融合理论进行证据合成。

Step 4根据融合后的结果，判断每个补偿电容是否存在故障。

3 试验验证

试验以高速综合检测列车的检测数据为依据，分别选取A、B两个典型区段某月的动态检测数据，对所提出的补偿电容故障判决方法有效性进行验证，区段基本信息见表1。

表1 典型区段基本信息

1）区段A补偿电容脉冲检测和感应电压原始数据分别见图5（a）和图5（c），经过数据预处理后的补偿电容脉冲检测和感应电压检测数据分别见图5（b）和图5（d）。按照图2所示步骤对区段A数据进行故障识别。基于补偿电容脉冲检测的故障识别结果显示，该区段补偿电容均正常；基于感应电压的故障识别结果显示，感应电压特征数据极值点在误差允许的范围内与补偿电容位置一一对应，补偿电容均正常；基于D-S证据融合理论，对以上单一判定结果进行融合，最终按照融合规则得到本区段的补偿电容正常概率均在98%以上，即不存在补偿电容故障，与实际情况相吻合。

图5 区段A感应电压和补偿电容数据

2）区段B补偿电容脉冲检测和感应电压原始数据分别见图6（a）和图6（c），经过数据预处理后的补偿电容脉冲检测和感应电压检测数据分别见图6（b）和图6（d）。按照图2所示步骤对区段B数据进行故障识别，具体结果见表2。

表2 区段B补偿电容故障判决结果 %

图6 区段B感应电压和补偿电容数据

由表2可以得出，基于补偿电容脉冲检测的判别结果：C11故障概率为71.3%，C13故障概率为79.7%，其余电容正常概率远大于故障概率，即故障电容为C11、C13。基于感应电压检测数据的判别结果：C13故障概率为100%，其余电容正常概率远大于故障概率，即故障电容为C13。使用D-S证据融合理论对2种方法补偿电容正常/故障概率进行融合，输出的判定结果为C13故障概率为79.7%，其余电容正常概率远大于故障概率，最终输出故障电容只有C13，有效降低了误报率。

结合某线路100个区段共计1 094个补偿电容的实测数据，对基于补偿电容脉冲、基于感应电压及基于D-S证据融合理论的补偿电容故障识别准确率进行对比分析，结果见图7。相比基于补偿电容脉冲、感应电压的单一来源数据故障识别方法，利用D-S证据融合理论融合后的补偿电容故障识别准确率分别提升了13%和5%。

图7 3种方法的补偿电容故障准确率

4 结论

基于D-S证据融合理论的补偿电容故障判决方法，可分别对基于补偿电容脉冲检测数据与感应电压数据提取的代表补偿电容状态特征值进行正常/故障概率分配，利用D-S证据融合理论，对单一判定结果进行融合，得到每个补偿电容的故障概率，以实现补偿电容故障识别。基于实际数据的试验结果显示，该方法可有效排除误判情况；相比单一来源数据故障识别方法，利用D-S证据融合理论融合后的补偿电容故障识别准确率得到有效提升，为提高铁路信号动态检测补充电容故障识别率提供了参考与支撑。