基于改进GWO-SVR 算法的锂电池剩余寿命预测

金 辉，胡寅逍，葛红娟✉，郝志鹏，曾郑志远，唐泽鹏

1) 南京航空航天大学民航学院，南京 211106

2) 中国民航科学技术研究院，北京 100028

锂离子电池具有能量密度高、使用寿命长、体积小重量轻等优势[1-2]，已经成为了机载蓄电池的发展趋势[3].随着充放电次数增加，锂电池性能退化，电池容量降低，剩余使用寿命（Remaining useful life,RUL）减少[4-5].以B787 机载锂电池热失控为代表的系列事故暴露出机载锂电池的安全管理问题[6].容量是反映电池性能水平的一项重要指标[7]，目前机务人员主要通过满容量充放电法检测电池容量从而判断其性能水平，但该方法成本较高且会消耗电池寿命.寻找可靠方法监测锂电池性能进行准确的RUL 预测，对机载锂电池的安全管理与航班安全运行至关重要.

国内外学者针对锂电池RUL 预测开展了诸多研究，所用方法主要分为基于模型和数据驱动两种[8].基于模型的RUL 预测方法需要分析锂电池的内部结构、电化学特性和失效机理，从而建立电池性能退化模型开展预测[9].Khodadadi Sadabadi 等[10]基于锂电池的电化学特性提出一种增强单粒子模型，对车载锂电池进行RUL 预测.El Mejdoub 等[11]以锂电池老化条件为输入建立性能退化模型，通过评估容量和电阻的变化趋势实现RUF 预测.此类方法均需要分析电池退化机理，预测精度由性能退化模型的准确程度决定[12].机载蓄电池工作条件恶劣、环境因素复杂，难以建立准确的退化模型.

数据驱动方法则基于电池充放电数据实现RUF预测，无需分析电池内部机理，泛化性和精度好且成本较低[13].魏孟等[14]从锂电池放电数据中提取间接健康因子，基于非线性自回归动态神经网络建立了锂电池RUL 预测模型.徐佳宁等[15]基于支持向量回归（Support vector regression,SVR）算法建立锂电池RUL 预测模型并提出一种改进蚁狮优化算法调整SVR 参数，提高了锂离子电池RUL 预测的准确性.Zhang 等[16]利用相关分析法在增量容量曲线中提取特征，利用人工神经网络建立RUL 预测模型.

采用数据驱动的方法进行锂电池RUF 预测，通常需要借助寻优算法对模型训练算法的参数进行寻优.近年来，具有收敛性能强、参数少等优点的灰狼优化算法（Grey wolf optimization,GWO），得到了研究者的关注和广泛应用[17].王岩韬等[18]面向雷暴天气下区域内多航班集体备降问题，基于GWO 提出一种多航班备降动态优化方案；王桥等[19]采用GWO 算法对极限学习机的超参数进行优化，建立了锂电池荷电状态评估模型.

实际应用中，GWO 算法存在容易陷入局部最优的问题[20].针对此问题，本文对GWO 算法中的核心表达式——位置更新方程进行改进，为狼群引入飞行和记忆能力，并采用Skew Tent 映射对狼群初始位置分布进行优化，提出一种改进灰狼优化算法（Improved grey wolf optimization,IGWO）.采用19 种标准测试函数对比了IGWO 和GWO 算法的寻优能力，证明IGWO 具有更好的寻优精度和收敛能力.进一步，论文基于容量增量分析和灰色关联分析等算法从锂电池的电压、电流数据中提取并筛选特征，提出基于IGWO-SVR 的锂电池RUL预测方法，并利用NASA 锂电池数据集开展验证实验.结果表明，本文所提方法能够实现更加准确的锂离子电池RUL 预测.

1 基于IGWO-SVR 的RUF 预测模型构建方法

1.1 支持向量回归与灰狼优化算法

SVR 基于训练集T={(x1,y1),···,(xN,yN)}训练模型，其中xi和yi分别对应第i个样本的输入向量和输出值.训练过程中，SVR 利用非线性映射ϕ(x)将训练集从低维空间映射到高维空间，该过程表达式为：f(x)=ωϕ(x)+b，ω和b分别代表权重与截距.SVR 根据结构风险最小化原则求解f(x)的过程可以表示为求解约束最优化问题[21]：

其中：C为惩罚参数，负责调节样本回归模型的复杂性与样本拟合精度；分别代表上下界的松弛变量；ε代表不敏感损失因子.

引入拉格朗日乘法算子和对偶原理，基于序列最小优化算法求解得到最优拉格朗日乘数参数.引入核函数，得到非线性映射SVR 表达式为：

其中，K(xi,x)=ϕ(xi)ϕ(x)代表核函数.

本文选取普适性好，应用广泛的径向基核函数（Radial basis function,RBF）作为核函数，其表达式为：KRBF(xi,x)=exp(-γ‖xi-x‖2)，其中γ=1/(2σ2)为核参数，σ为带宽参数.

在SVR 中，惩罚参数C、不敏感损失因子ε和核参数γ是影响其预测性能的主要参数，为了提高预测精度，本文采用灰狼优化算法对这三个参数进行寻优.

自然界的狼群具有严格等级制度，通常分为α、β、δ 和w 四个等级，对应在GWO 算法中的最优解、次优解、季优解以及所有候选解.假设狼群规模为NW，代表第i只狼所处位置，S代表寻优空间维数（即寻优参数数量），GWO寻优过程中狼群各行为的表达式为[22]：

1）包围猎物：设第i只狼与猎物之间距离为Di=，包围猎物过程的数学表达如下：

2）搜寻猎物：灰狼个体i搜寻猎物的过程主要依靠位置更新方程实现，表达式如下：

式中：Xɑ、Xβ和Xδ分别代表α、β 和δ 狼所处的位置；Diɑ、Diβ和Diδ分别代表第i个灰狼与α、β 和δ 狼之间的距离；Xi1、Xi2和Xi2分别代表第i个灰狼向α、β 和δ 狼方向移动的目标位置.

3）攻击猎物：A的取值在[-a,a]区间内，在迭代过程中，a的值线性递减，使得A的变化范围随之减小，从而模拟逼近猎物.

1.2 增加记忆功能的改进灰狼优化算法

GWO 算法借助组件Pr的随机性提供全局搜索，一定程度避免陷入局部最优.但是在实际应用中，尤其是求解多峰值问题时，GWO 仍然常会面临陷入局部最优，出现早熟收敛的问题.针对该问题，本文对GWO 算法的种群初始化方法和位置更新方程进行优化改进，提出改进灰狼优化算法IGWO.

在GWO 算法中根据寻优变量的上下界设置来随机初始化灰狼个体的位置，这种方法存在位置初始分布不均匀的风险，制约收敛速度.混沌具有随机性和遍历性和初值敏感性，能使算法有更快的收敛速度.为了使初始种群个体尽可能地利用解空间的信息，本文采用 Skew Tent 映射[23]产生混沌序列用来对IGWO 进行种群初始化.基于Tent映射生成混沌序列的过程的数学表达式如下：

式中，φ为映射参数，取值在（0,1）之间，Ti和Ti’分别代表种群中第i个样本在映射前后的位置.

在范围为（0,100）的一维空间中，对个体数量为10 的种群，采用随机生成方式和Tent 映射分别进行了十次种群初始化，效果如图1 所示.图中横纵坐标分别代表迭代次数和个体所处位置.可以看出，采用Tent 映射进行种群初始化，在不同迭代次数下的个体分布情况都更加均匀.

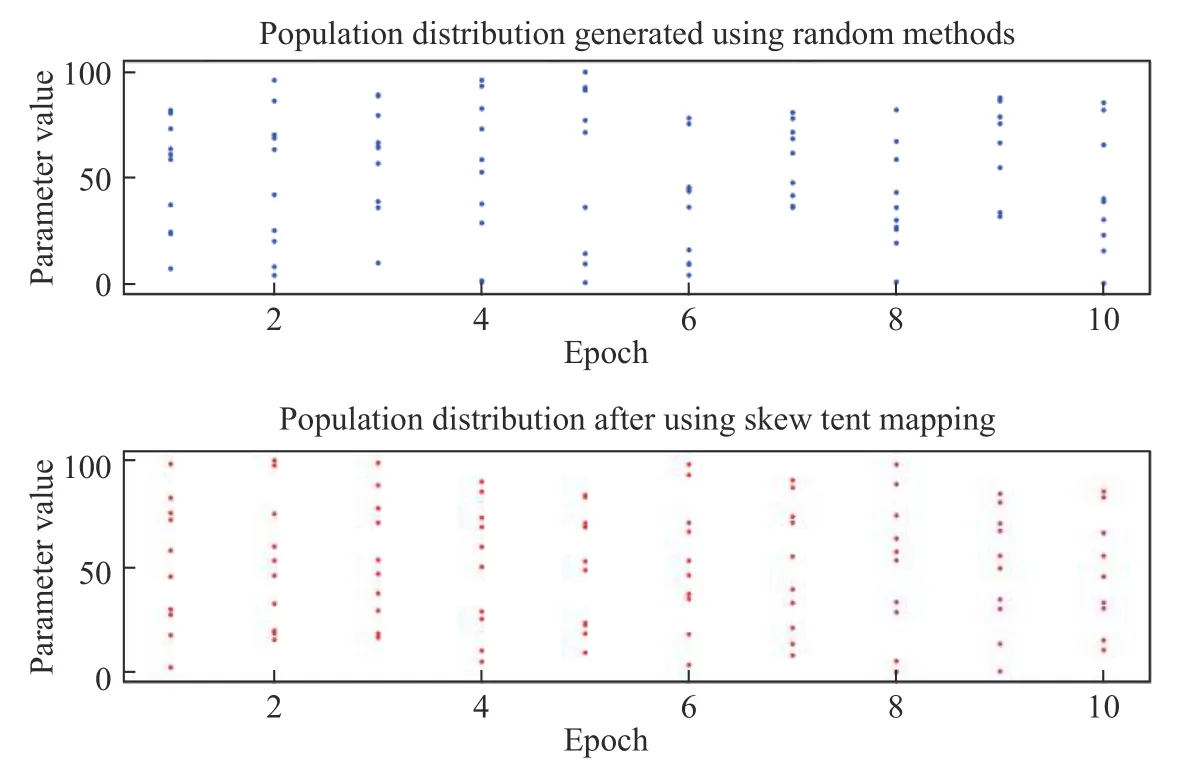
图1 随机方式与Tent 映射产生的种群分布效果对比Fig.1 Comparison of population distribution generated by the random method and tent mapping

随后，通过引入Levy 飞行[24]，使得距离α、β、δ 狼较远（即 |A|≥0.5）的个体增强搜索范围，得到新的位置更新方程：

式中，s为步长，可表示为s=u/|v|1/λ，其中u和v均为正态分布随机数，λ为飞行参数.

μ为步长控制因子，表示步长的控制量，通常等于1，但是μ固定取值下的搜索能力较差，且无法在搜索过程中提供准确性.

因此，本文提出一种新型随机动态控制因子μ，使算法随着迭代而逐渐收敛，表达式如下：

其中，R∈[0,1]，是满足正态分布的随机数.

与线性递减因子相比，随机动态控制因子随着迭代次数增加逐渐衰减为0 的同时，额外引入了取值随机性：μ取值在下降过程中随机波动，迭代次数越小，波动幅度越大，从而增强了算法在迭代前中期的搜索能力.

在此基础上，为进一步增强算法的探索能力和加快收敛速度，IGWO 借鉴粒子群寻优算法中对粒子自身运动历史最优解进行记忆保存的思想，对灰狼增加记忆功能：在迭代过程中保存每个灰狼的历史最优位置记录，使狼群在靠近记忆中的最佳位置时，在听从α 狼指挥的同时也会参考自身记忆进行移动.

最终提出一种改进位置更新方程为:

其中，Xih代表灰狼i所经历的历史最佳位置，Dih代表灰狼i当前位置和历史最佳位置的距离.

这种改动引入了个体自身最优位置记忆，理论上可以加强算法的开发能力以及加快收敛速度.

1.3 基于IGWO-SVR 的锂电池RUF 预测

提出利用IGWO 算法对SVR 的惩罚参数C、不敏感损失因子ε和核参数γ进行寻优，建立锂电池RUF 预测模型的流程，如图2 所示.

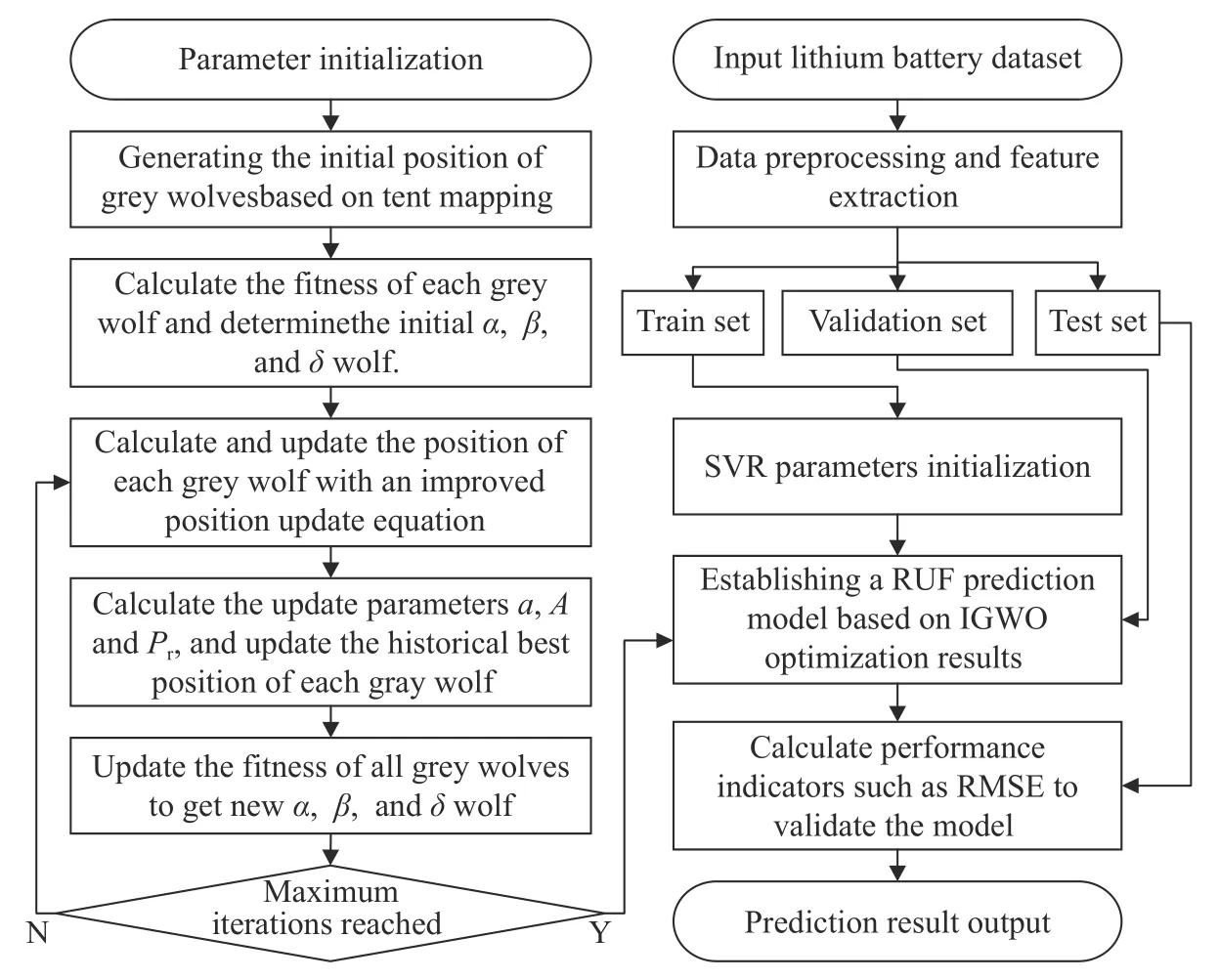
图2 基于IGWO-SVR 的锂电池RUL 预测流程Fig.2 RUL prediction and performance assessment process of lithium-ion batteries based on IGWO-SVR

基于IGWO-SVR 开展锂电池RUL 预测的具体过程如下：

1）数据处理：对锂电池充电数据集进行预处理，从锂电池充电电压、电流等可监测外特性参数中提取特征，并根据相关性分析结果筛选特征集合，最后根据设定的预测起点划分训练集、验证集和测试集.

2）参数设置与初始位置生成：设置狼群规模为30，最大迭代次数为500，惩罚参数C、不敏感损失因子ε和核参数γ的寻优边界范围依次为（0.1，10000）、（0.001，1）和（0.0001，1）；基于Skew Tent混沌序列生成灰狼个体初始位置.

3）建立适应度函数：根据当前迭代次数下的寻优结果，基于训练集建立RUL 预测模型.将验证集数据输入模型，计算实际容量值和预测值之间的均方根误差（Root mean square error,RMSE）作为适应度函数.

4）参数寻优：以验证集RMSE 最小为寻优目标，“狼群”根据式(9)改进位置更新方程在迭代中逐渐逼近参数C、ε和γ的最优组合.迭代至最大迭代次数后，根据寻优到的最佳参数组合，建立最终的锂电池RUL 预测模型.

5）开展RUL 预测：将测试集代入训练完成的模型进行RUL 预测，计算RMSE 等指标检验模型预测效果.

2 改进GWO 算法的寻优能力分析

本文中的所有实验均在Intel Core i5-12400F，2.5 GHz CPU,16G 内存的windows 11 系统下的PC上利用python 3.10 进行程序的编写、调试与运行.

采用IGWO 算法对19 个经典标准测试函数进行求解，并与标准GWO 算法的结果进行比较.其中，F1～F7 为单峰测试函数，F8～F19 为多峰测试函数.

在对比实验中，GWO 和IGWO 算法的种群规模均设置为30，最大迭代次数均设置为500.采用GWO 和IGWO 对各个测试函数均进行10 次寻优，分别统计最优精度值(Best)、平均精度值(Mean)、最差精度值(Worst)和精度标准差值(St.dev)，得到表1.其中，Best、Worst 反映了解的质量；Mean 代表在给定的迭代次数下算法最终所能达到精度的平均值，反映了算法的收敛速度；St.dev 反映了算法的稳定性和鲁棒性.

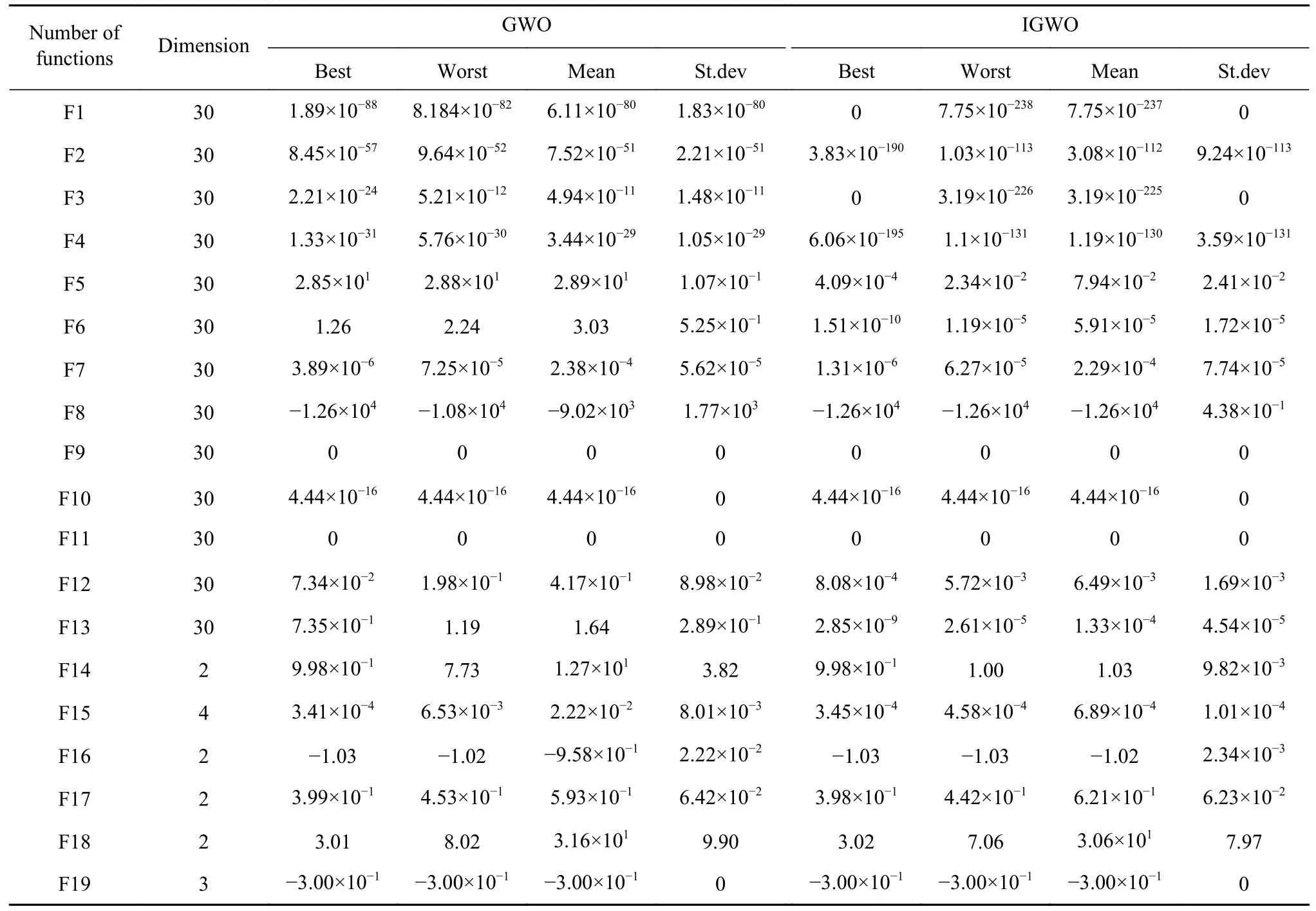
表1 标准测试函数寻优结果Table 1 Results of benchmark problems

从表中结果可见，本文提出的IGWO 算法在大部分标准测试函数上性能优于传统GWO 算法.除了在F9 到F11 和F19 上IGWO 与GWO 算法寻优结果相同外，其他函数上，IGWO 算法均取得了更好的平均精度值.在F1 到F4 标准测试函数上，IGWO 算法的优势最明显，平均寻优精度提升了数十乃至上百个数量级.对于函数F1 和F3，使用IGWO算法能够寻找到GWO 算法未能找到的最优解0.

图3 给出了在其中一次试验中，IGWO 算法与GWO 算法在F4～F11 测试函数上的收敛曲线.可以看出，在测试函数F4～F7 上，IGWO 算法能够更有效的避免局部最优，取得更好的收敛精度.在F8～F11 上，虽然IGWO 和GWO 最后取得的寻优精度相同，但是IGWO 的收敛速度更具优势.

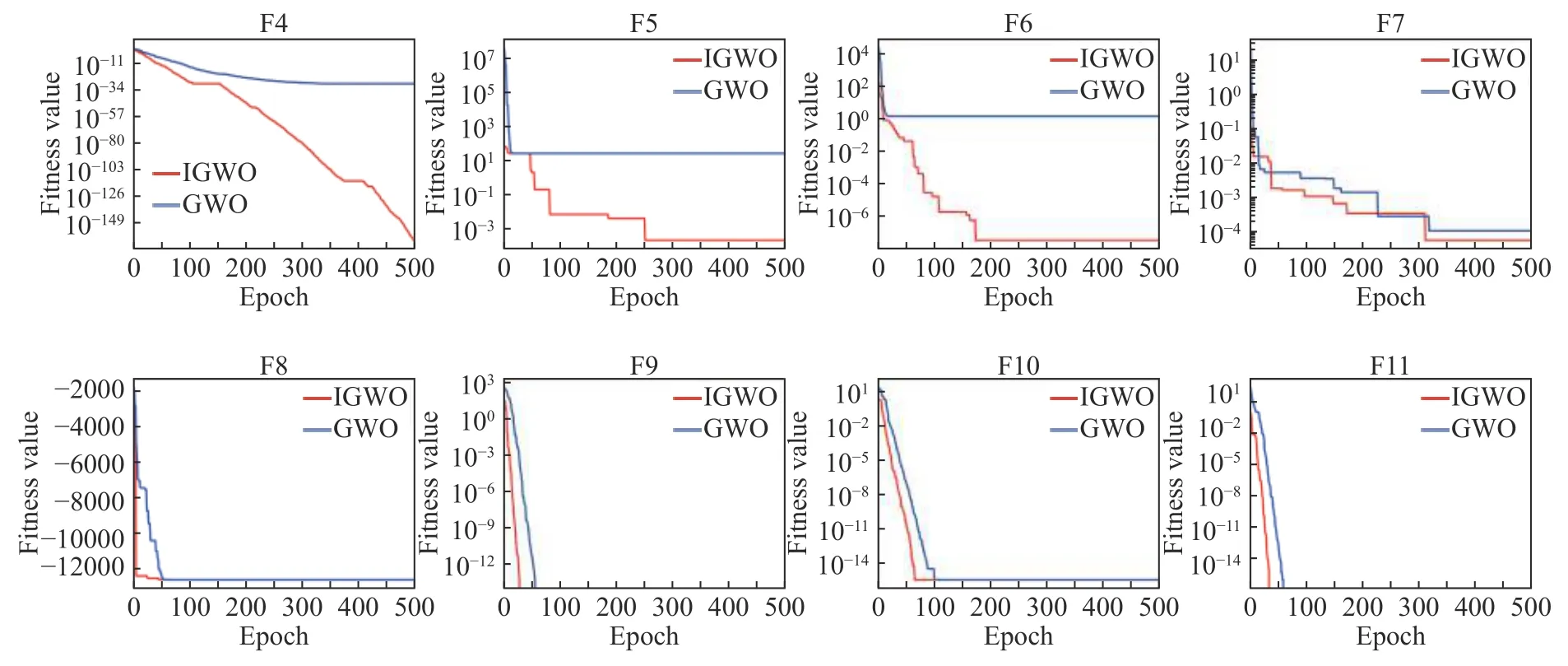
图3 IGWO 与GWO 在测试函数F4～F11 上的收敛曲线Fig.3 Convergence curves of the proposed IGWO and GWO for F4-F11

3 基于IGWO-SVR 的锂电池RUL 预测方法验证

3.1 基于容量增量分析的锂离子电池特征提取方法

本文使用美国航空航天局NASA 公开的锂离子电池实验数据集进行实验.NASA 实验过程中，所有电池均采用恒流-恒压模式（Constant currentconstant voltage,CC-CV）进行充电：电池充电阶段以1.5 A 恒流CC 模式充电至电池电压达到4.2 V，然后以恒压CV 模式继续充电至充电电流降到20 mA.对于本文采用的B0005、B0006、B0007 和B0018电池，放电阶段以2 A 电流恒流放电直到电池电压分别下降到2.7、2.5、2.2 和2.5 V.

通过观察不同循环次数下采集的充放电电压、电流及温度数据发现，电池容量与充电次数，总充电时长，CC 充电时长，CC 放电时长等特征密切相关.除了这些可以直接观察到的特征外，电池充电数据中还蕴含着反映电池内在特定化学反应过程的微分特征[25].容量增量分析（Incremental capacity,IC）是提取锂电池微分特征的常用方法.

本文将时间变化作为数据采样的判定指标，从锂电池充电电压数据中获取容量增量数据绘制IC 曲线.采样时间间隔参考经验值设置为10 s.随后，基于Savitzky-Golay 滤波和卡尔曼滤波对不同循环次数下的IC 曲线平滑降噪，得到图4.

观察对比IC 曲线的变化可以看出：随着电池容量的下降，IC 曲线的起点逐渐右移；电压3.8 V到4.1 V 区间的IC 曲线波峰面积随之下降；电压4.1 V 之后的IC 曲线末端均值减少.

灰色关联分析算法能够根据不同因素间变化趋势的相似程度解算灰色关联度，量化不同因素之间的关联程度[26].本文采用灰色关联分析算法，在不同电池的数据上分别计算上述特征与容量之间的关联程度，结果如表2 所示.

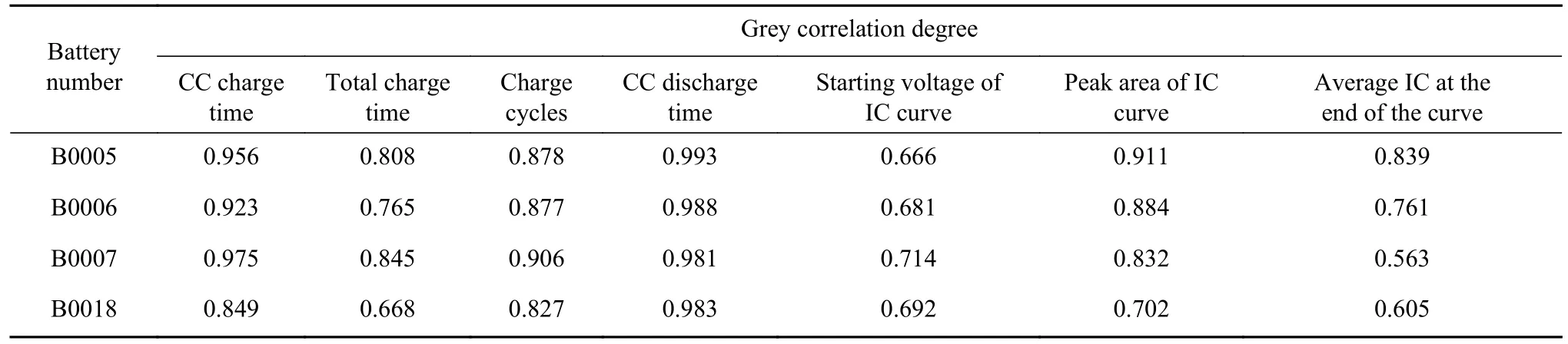
表2 各项特征与电池容量的灰色关联度Table 2 Grey correlation degree between various features and battery capacity

可以看出，CC 充电时长、充电次数、CC 放电时长和IC 曲线波峰面积四项特征，在不同电池的数据中与电池容量的灰色关联度均较高，显著高于其他几项特征的灰色关联度.因此，根据灰色关联分析结果，本文筛选出CC 充电时长等四项特征组成特征集，开展锂电池剩余寿命预测试验.

3.2 锂电池RUF 预测效果对比实验

使用NASA 数据集，分别基于SVR、GWO-SVR和IGWO-SVR 训练建立预测模型，对比算法效果.对于SVR，设置其惩罚参数C=10，核参数γ=0.01，不敏感损失因子ε=0.1.GWO 和IGWO 设置同上节所述.在使用GWO 和IGWO 算法寻优过程中，使用预测起点之前的数据组成训练集，将预测起点之后的数据用于测试.为避免过拟合，将训练集中的前半部分用于训练，使用全部的训练集数据进行验证，以验证结果的均方根误差最小为目标进行参数寻优.

在NASA 锂电池实验中，大部分电池经历了160 余次充放电循环，且电池寿命终止均发生在中间值80 次以后，因此本文首先选择充放电循环次数达到80 作为预测起点进行实验.为了对比验证在预测周期更长的场景下，不同算法的预测效果，将循环次数60 作为预测起点进一步开展实验.

当预测起点设置为80 时，基于SVR、GWO-SVR和IGWO-SVR 训练得到模型的RUL 预测结果见图5，图中蓝色折线为电池容量的实际值，黑色竖线代表预测起点的充放电循环次数（80 次），灰色横线代表寿命终止阈值的电池容量（1.42 A·h）；绿色、橘色和红色折线依次代表使用 SVR、GWO-SVR和IGWO-SVR 的预测结果，同色系竖线则分别标注出了电池实际寿命终止时循环次数和不同算法预测的循环次数.

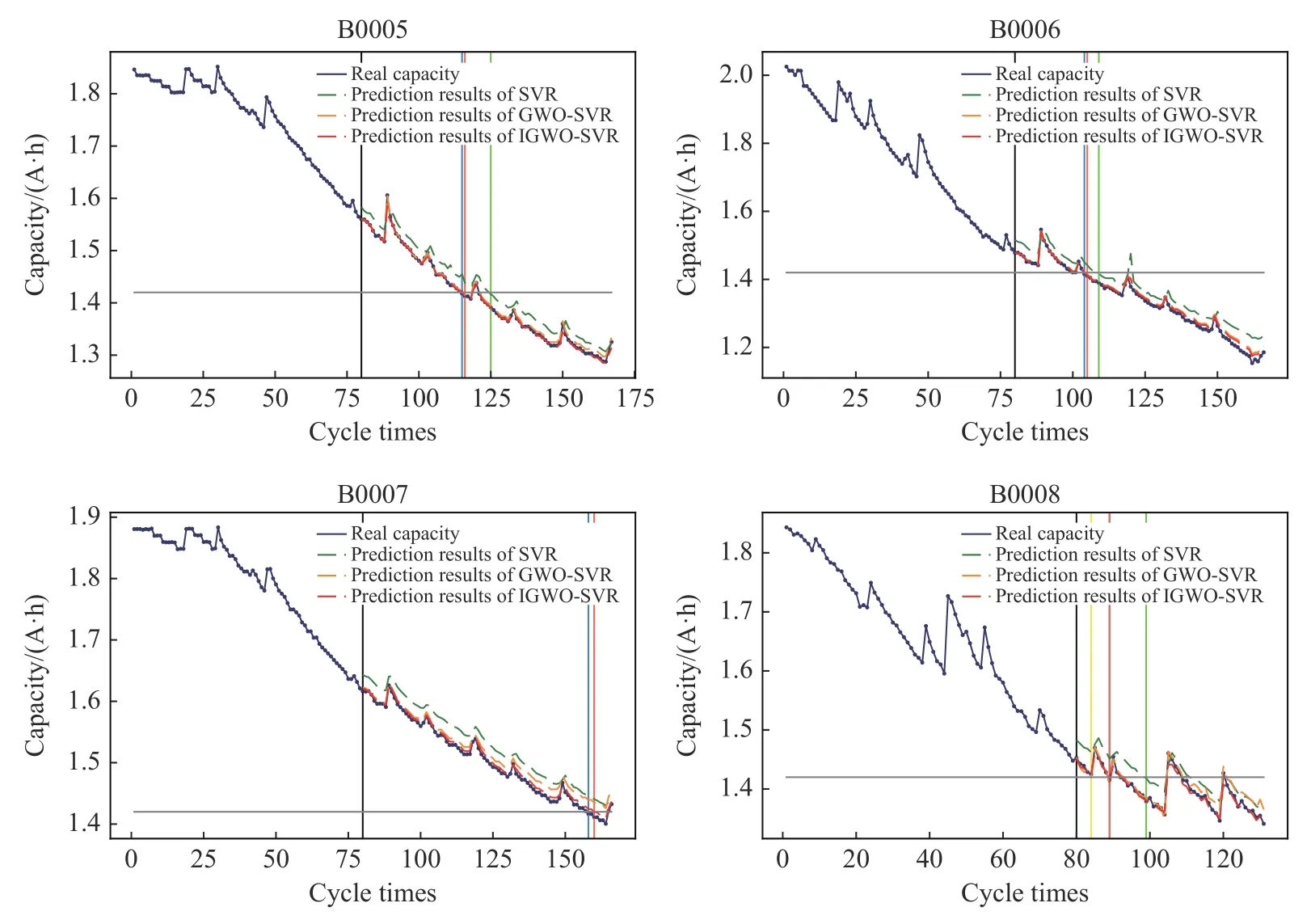
图5 基于三种算法的锂电池RUL 预测结果(80 cycles)Fig.5 RUL predictions of lithium-ion batteries based on three algorithms (80 cycles)

b 从图中可见，三种算法均能够不同程度的预测电池的容量衰退，且有效识别出容量回升，说明本文选取的特征组合有效.在引入GWO 和IGWO算法进行参数寻优后，RUL 预测效果显著提升.与GWO-SVR 相比，使用IGWO-SVR 训练模型的预测结果均更接近真实值，说明本文提出的IGWO算法在锂电池数据集上也有着更好的寻优能力，能够跳出GWO 训练过程中陷入的局部最优.

将预测起点左移至循环次数为60 处，使得预测周期变长，此时基于 SVR、GWO-SVR 和IGWOSVR 训练得到模型的RUL 预测结果如图6 所示.对比可见，在预测周期更长的场景下，各个算法的预测结果与真实值之间的偏差明显变大，IGWOSVR 的预测结果相对最好，在不同电池数据上预测的RUL 值均最接近真实值.

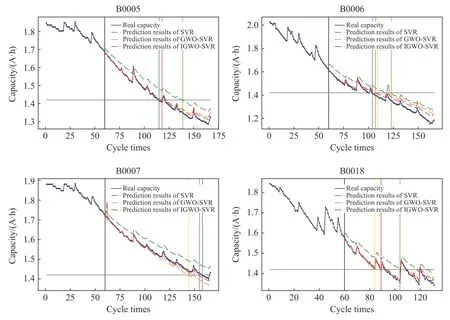
图6 基于三种算法的锂电池RUL 预测结果(60 cycles)Fig.6 RUL predictions of lithium-ion batteries based on three algorithms (60 cycles)

统计预测起点分别为80 次循环和60 次循环时，各个算法训练的模型对不同锂电池的RUL 预测结果得到表3.其中，RUL 一列代表各个电池的实际剩余使用寿命，RUL-P 代表相应算法的预测值，Er 则代表RUL 和RUL-P 之间误差的绝对值.预测起点为80 次循环时，对于7 号电池，采用SVR和GWO-SVR 算法预测的RUL 值未达到失效阈值，因此其RUL-P 和Er 均用“—”表示.

表3 不同算法的锂电池RUL 预测效果Table 3 RUL predictions of lithium-ion batteries under different prediction starting points

可以看出，采用IGWO-SVR 算法取得的预测效果更好，在18 号电池上实现了与真实值一致的RUL 预测结果.在预测周期最长的7 号电池上，IGWO-SVR 算法性能优势明显，预测误差明显更低.对于5 号和6 号电池，IGWO-SVR 和GWO-SVR的RUL 预测结果相近.为了进一步对比三种算法的预测精度，统计电池容量预测结果与真实容量值之间的均方根误差（Root mean square error,RMSE）和平均绝对百分误差（Mean absolute percentage error，MAPE）值，得到表4.

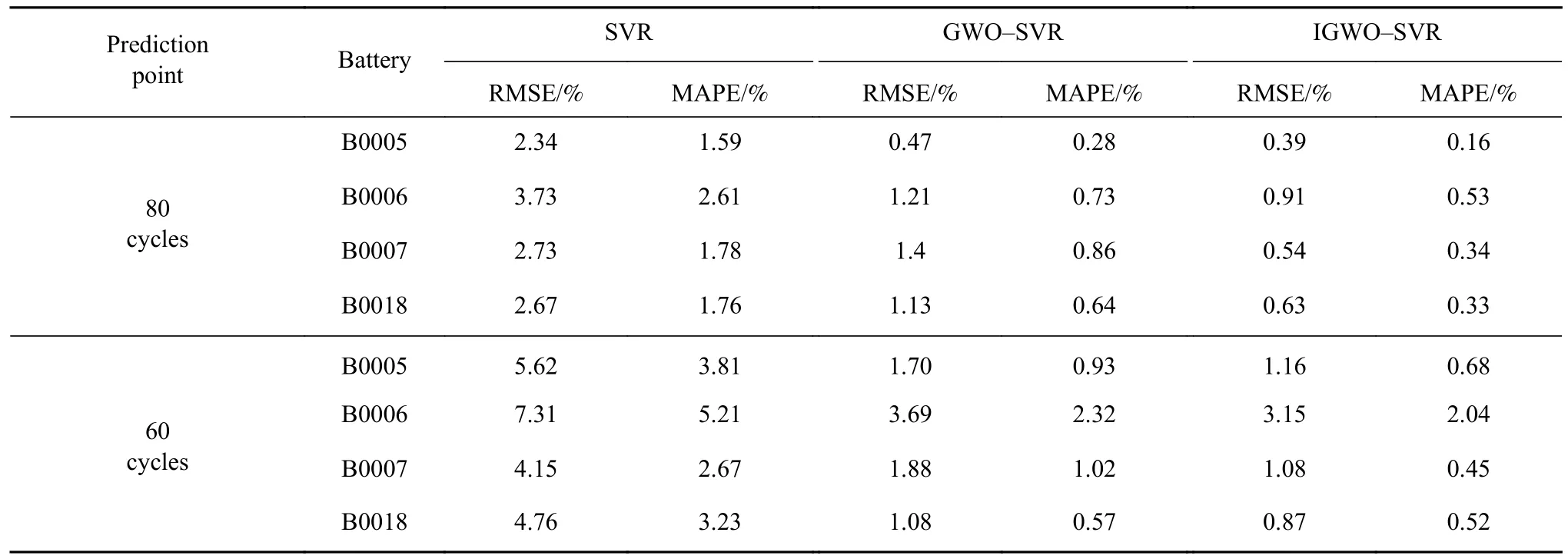
表4 不同算法的容量预测误差Table 4 Capacity prediction error of different algorithms

分析表4 数据可见，进行参数寻优后，不同预测起点下SVR 算法在全部四块电池上的预测误差都显著降低，RMSE 值和MAPE 值均降低一倍以上.在不同预测起点和电池的数据上，使用IGWOSVM 取得的RUL 预测精度均最高，与GWO-SVR相比RMSE 和MAPE 值至少降低了10%；在预测起点为80 cycle 时，IGWO-SVM 对不同电池数据的预测结果均与真实值高度接近，RMSE 值均在1%以内.对于5 号和6 号电池，虽然IGWO-SVM与GWO-SVR 的RUL 预测结果相近，但是IGWOSVM 的容量预测效果更好，不同预测起点下的RMSE 和MAPE 值都显著更低.本文提出的IGWO算法性能较好，在优化SVR 参数训练锂电池RUL预测模型的应用场景，能够取得比GWO 算法更好的优化效果.

4 结论

本文基于容量增量分析等方法从锂电池充放电数据中提取并筛选得到CC 充电时长、IC 曲线波峰面积等特征，使用SVR 算法训练RUL 预测模型，并引入GWO 算法进行参数寻优.针对标准GWO算法容易陷入局部最优的问题，对传统位置更新方程进行改写，引入个体记忆能力提出一种改进灰狼优化算法IGWO.开展对比试验验证提出的IGWO 算法性能，结论如下：

（1）基于19 个标准测试函数开展IGWO 和GWO 优化效果对比试验，结果表明IGWO 在寻优精度和收敛速度上均更具优势.

（2）基于NASA 实验室的锂电池数据集开展实验，对比SVR、GWO-SVR 和IGWO-SVR 训练模型RUL 预测效果，证明基于IGWO-SVR 建立的模型能够显著提升RUL 预测精度，在不同电池数据上的预测结果的均方根误差均下降了10%以上.

研究下一步考虑将提出的IGWO 算法应用于其他机器学习算法参数寻优、大规模函数优化、约束优化等优化问题中，进一步检验算法效果.