具有低开关频率的感应电机无传感器控制

齐 昕，任佳仕，石向阳，赵宇航，李凌一

1) 北京科技大学机械工程学院，北京 100083

2) 北京科技大学顺德创新学院，佛山 528399

交流感应电机在工业中的应用极为广泛，其功率范围宽，是经济行业及日常生活应用最为广泛的电动机.在工业生产中，多数感应电机的应用环境较为恶劣，且对使用成本有着较高的要求.在感应电机控制系统中，无速度传感器控制相较于有感控制会降低系统复杂性，同时降低系统硬件成本，提高系统可靠性和环境适应能力.无速度传感器控制方法实现的关键在于转子磁链和转子转速的精确观测.目前无速度传感器的转子磁链及转子转速观测方法主要有两类：一类是基于电机数学模型的开环或闭环观测方法，如：电压模型法、模型参考自适应系统(MRAS)观测法[1-2]、龙贝格观测器(LO)[3-4]、滑模观测器(SMO)[5-6]、扩展卡尔曼滤波(EKF)观测法[7]等；另一类是基于电机非理想特性的方法，如高频信号注入法[8-9]等.

无速度传感器的转子磁链及转子转速观测方法中，滑模观测器具有估计精度高、完全自适应、鲁棒性强、动态响应快等优点[10]，受到了广泛关注.滑模控制算法根据估计的定子电流与实际定子电流之间的误差确定滑模控制函数，使控制系统的状态最终稳定在设计的滑模面上[11].Wang 等[12]将滑模控制理论应用于模型参考自适应系统，可以补偿直流母线电压漂移和不平衡电流的不利影响，提高观测精度.孙佳将等[13]针对传统滑模观测器容易受到定子电阻变化的影响，设计了一种与磁链观测偏差相关的函数，直接对磁链进行控制.赵德宗等[14]在滑模控制函数前加入了可变增益，提出了一种收敛速度可调的滑模观测器，具有更强的鲁棒性.Yan 等[15]设计了双坐标系滑模观测器，消除了速度估计和磁链估计之间的耦合，提高了观测器的鲁棒性.

在感应电机控制系统中，逆变器的开关频率是影响感应电机控制系统性能及逆变器使用寿命的重要因素之一.若开关频率过高，则会增加逆变器的开关损耗，使开关器件发热严重，导致逆变器输出功率降低，甚至损伤逆变器开关管，缩短逆变器使用寿命.因此，为减小开关管损耗，提高逆变器输出功率，应当尽可能降低开关频率[16-17].常用的降低逆变器开关频率的方法有基于空间矢量脉宽调制SVPWM 的低开关频率控制方法以及预测控制方法.

传统的基于SVPWM 的低开关频率控制方法在降低开关频率的同时，系统采样频率也会随之降低，从而会使数字控制系统产生较大的时间延迟，使控制带宽降低，进而导致矢量控制的动态响应能力下降.而系统延时增加也会导致观测器的观测精度随之降低.王晓帆等[18]通过提高采样速率降低了时间延迟带来的影响，并通过状态观测的方法对电流环进行了补偿.鄢永等[19]通过采用复矢量表示法对电流环延时环节进行精确建模，并提出一种基于误差补偿器的闭环电流预测延时补偿算法，提升了系统的鲁棒性.翁聪等[20]分析了系统延时对MRAS 观测器的影响，确定出了系统延时的大小，并通过相角调节器对观测器进行了补偿.但基于SVPWM 的低开关频率控制方法在低开关频率下始终不能保证高采样频率，这在无传感器的应用场景下，难以保证观测器的观测精度，从而难以达到较好的无传感器控制效果.

预测控制近年来在电力电子领域逐渐发展起来，其具有滚动优化的特点，根据约束条件不断滚动向前求取最优控制.冯凌等[21]将滞环概念引入预测控制中，将磁链、转矩等变量在滞环内的延伸长度作为选择标准，以此降低开关频率.乐胜康等[22]将逆变器开关损耗引入代价函数，通过在线预测调整选择出最优电压矢量.李耀华等[23]将开关次数考虑进代价函数，并采用自适应变权重系数的方法，有效地降低了开关频率，但计算比较复杂.齐昕等[24]基于图形边界限定形式的预测控制以电流为控制目标，将电流控制在限定边界内实现对电流的直接控制，无需设计权重系数.预测控制的开关频率与采样频率是独立的，在极低开关频率下可以保证高的采样频率.预测控制作为新兴的控制方法，其无速度传感器的研究尚不多见.Alkorta 等[25]以感应电机为参考模型，定子电压-电流模型和电流模型为自适应模型构建模型参考自适应系统，并与广义预测控制相结合，获得了优异的调速性能.

针对传统低开关频率控制方法带来的采样延迟问题，本文基于图形边界限定形式的预测控制实现了感应电机的低开关频率控制，同时保证系统具有较高的动态响应速度和控制精度，并实现了无传感器控制.这种基于图形边界限定形式的预测控制的本质是建立在电流矢量预测模型下，以低开关频率、高动态特性为控制目的的一种逆变开关策略，其通过建立电压矢量寻优准则实现直接电流控制.由于预测控制算法需要观测到的转子磁链、转子转速等信号参与预测，因此其无传感器算法实现时，观测器的观测精度对预测控制算法预测的准确性也至关重要.为了保证观测器观测的准确性和鲁棒性，本文通过转子磁链和定子电流为状态变量的感应电机数学模型构建了自适应滑模观测器，并进行实验验证了算法的可行性.

1 具有低开关频率高动态特性的控制方法

本文使用了一种边界限定形式下具有低开关频率、高动态特性的直接电流控制方法，其将电流环与逆变器作为一个系统整体考虑，以电流为控制目标，实现电流矢量的直接控制.此种控制方法摒弃了传统的调制控制策略，在每个采样周期内均通过标准电压矢量轮询法则选出一个最佳的标准电压矢量作用于电机.控制原理如图1 所示.

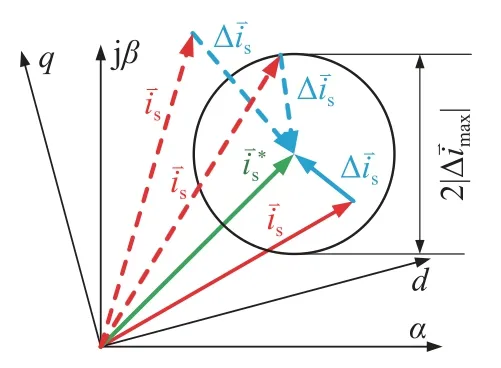
图1 电流矢量和边界圆Fig.1 Current vector and boundary circle

图中d、q、α、β均为坐标轴，j 为虚数单位，以参考定子电流矢量的顶点为圆心，最大允许电流偏差值为半径，构造圆形边界.持续监测实际定子电流矢量并计算电流偏差，当时，预测模型轮询计算所有可能的开关状态，选择能够使得电流轨迹维持在边界内最长时间的基础电压矢量作为最优电压矢量，重新作用在电机上，从而降低逆变器开关频率.预测模型及最优电压矢量轮询方法为：

假设当前时刻为t0，记经过时间 Δt后的时刻为t，未来t时刻参考电流矢量为，在k号电压矢量作用下预测电流矢量为，未来t时刻的电流矢量偏差可表示为：

式中，k代表电压矢量号，如图2 所示，其中：

图2 三相两电平电压源逆变器空间电压矢量Fig.2 Three-phase two-level inverter space voltage vector

其中

式(1)～(3)，求平方可得未来t时刻电流偏差的平方如式(6)所示.

二次函数的右根即为电流轨迹可以在边界内保持的时间 Δt，产生最大右根的二次函数曲线所对应的基础电压矢量即为最优电压矢量.这种电压矢量寻优的方法是通过直接改变基础电压矢量的方式，使得基础电压矢量直接作用于电机，没有目标电压矢量的调制过程，因此其在降低逆变器开关频率的同时，实现了迅速的电流响应.

图3 为预测控制电流环测试时的d-q轴电流，id、iq分别为定子电流的d、q轴分量.0.1 s 时q轴电流由0 A 突变到5.6 A，实际q轴电流迅速上升，响应时间只有1.52 ms.该情况下系统的开关频率仅500 Hz 上下，开关频率定义为一秒中逆变器单个开关管的动作次数.而单采样的SVPWM 算法若要实现500 Hz 的开关频率，则系统的采样频率需要降到250 Hz，因而系统以250 Hz 的频率计算占空比.由于电流环基于比例积分控制器(Proportionalintegral controller,PI controller)调节，其存在动态响应慢的问题，且采样频率越低动态响应越慢.在250 Hz 的采样频率下，PI 调节器的动态响应时间必定大于4 ms，远远大于预测控制的电流响应时间.

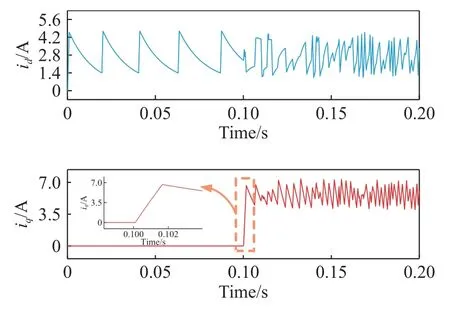
图3 预测控制电流环动态测试d-q 轴电流Fig.3 d-q axis current during the predictive control current loop dynamic test

2 转子磁链和转子转速的观测

为了解决传统的电压型磁链观测器观测精度不高的问题，同时实现预测控制下的无传感器控制，本文提出了基于滑模原理的感应电机速度自适应滑模观测器.

2.1 感应电机速度自适应滑模观测器

滑模观测器是一种根据系统的输入变量和输出变量的实测值得出状态变量估计值的一类动态系统，其使用非线性高增益反馈矩阵迫使估计的状态变量逼近预先设定的滑动超平面，以使得估计输出等同于测量输出.

由于预测控制算法中，电流矢量预测的准确性极易受到转子磁链和转子转速等信息的影响，而图4 所示观测模型是一种开环观测模型，磁链观测器本身的观测准确性容易受到参数扰动和采样误差的影响，进而影响预测控制算法中电流矢量的预测准确性.因此，必须使用闭环磁链观测器，以提高磁链观测的准确性.

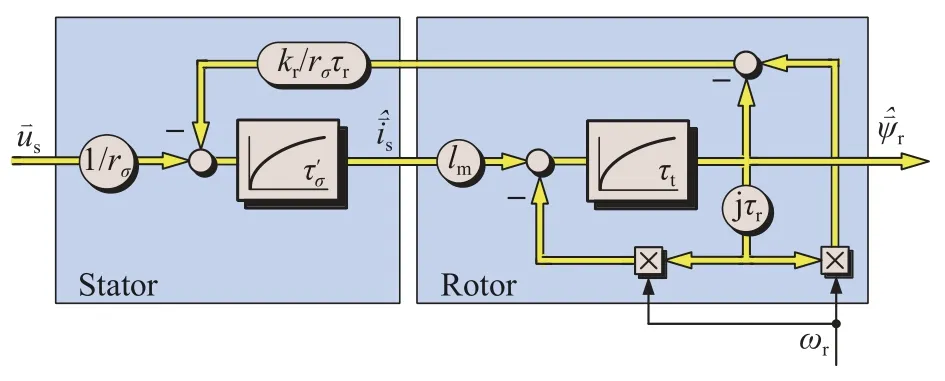
图4 开环转子磁链观测器信号流图Fig.4 Signal flow diagram of the open loop rotor flux observer

在图4 所示开环观测器的基础上构建闭环观测器，选择以观测的定子电流与实际定子电流之间的偏差量作为反馈信号.为进一步提高观测器的抗扰动能力，本文在原有的观测器基础上引入滑模控制理论，通过构建滑动超平面的方式，迫使估计输出逐渐等同于测量输出，使观测器观测的定子电流值逐渐收敛到实际的定子电流值，从而实现转子磁链的精确观测.

图5 滑模观测器原理示意图Fig.5 Schematic of the the principle of sliding mode observer

在滑模控制理论中，滑模增益的设计十分重要，其决定了观测到的电流值会不会收敛到实际的电流值，且决定了观测电流值的收敛速度.若滑模增益过小，则观测电流值收敛速度太慢，影响系统运行；若滑模增益过大，则会导致观测电流值剧烈振荡，增加观测误差.因此，本文搭建的滑模观测器中，反馈增益矩阵Gs和Gr的取值范围关系到观测器观测的稳定性、准确性和收敛速度.为保证滑模观测器正常运行，需要确定出反馈增益矩阵的取值范围.

根据滑模控制理论，滑模增益确定的过程即判定系统稳定的过程，而在现代控制理论中，通常使用李雅普诺夫定理判定系统是否稳定.因此，若证明在某个确定的反馈增益矩阵Gs和Gr的取值范围内，李雅普诺夫函数V对时间的导数为负定的，即系统大范围渐进稳定，则此反馈增益矩阵的取值范围内，观测值一定可以收敛到测量值.同时，由于观测器中转子转速无法确定，因此需要在构造转子磁链反馈增益矩阵Gr的同时，建立速度自适应观测模型，实现转子转速的自适应估计，并且保证观测系统稳定.

2.2 定子电流反馈增益矩阵 Gs取值范围确定

首先，对定子电流反馈增益矩阵Gs的取值范围和观测器的稳定性进行分析.

式(8)与(9)相减得到误差方程如式(10)所示：

已知李雅普诺夫函数V＞0恒成立，因此若要系统稳定，则需要V对时间的导数必须是负定的.V对时间的导数如式(12)所示：

若李雅普诺夫函数V对时间的导数为负定的，则反馈增益系数gs1、gs2应满足如下条件：

2.3 转子磁链反馈增益矩阵 Gr范围确定和速度自适应观测模型设计

根据滑模控制理论，当系统到达滑模面时如式(14)所示，其中表示定子电流矢量的导数，表示定子电流矢量观测值的导数：

此时，式(10)描述的观测器误差降阶为式(15)所示形式：

由式(15)整理得，在滑动模态下：

将式(16)带入式(15)，整理得：

定义李雅普诺夫方程：

其微分为：

将式(16)和(17)带入式(19)整理得：

整理可得：

若式(20)的第二、三项之和等于0 成立，则可得：

因此可以得到速度自适应估计模型如式(24)所示：

在实际应用中，将式（24）改写为如式（25）所示形式，以提高对速度估计的收敛速度，其中Kp、KI分别为PI 控制器的比例系数和积分系数.

由式(9)和式(25)构成速度自适应滑模观测器.

2.4 感应电机速度自适应滑模观测器的优化

在实际运行过程中，合适的滑模观测器参数设计会使得控制电流误差趋近于零，但是由于时间延迟等原因，在滑模面附近，系统会进入抖振状态，这种抖振状态严重影响系统稳定性.这是因为滑模控制系统本身是一种动态系统，其处于滑模面附近时，误差非常小，容易产生输出信号的正负切换，导致系统进入振荡状态.因此，可以选择饱和函数sat(s)替代符号函数sgn(s)，即在系统处于滑模面附近时，将原有的符号函数换成连续函数，从而避免系统进入振荡状态，减小系统抖振.饱和函数如式（26）所示，其中k为比例系数，s为函数自变量，通过调整 Δ的大小调整边界层的厚度.修正后的滑模控制系统在进入边界层后，状态反馈信号不再是简单的正负切换，而是在一定范围内连续变化，从而可以使系统逐渐稳定.

2.5 转子磁链和同步转速的计算

在预测控制算法中，需用到转子磁链角度信息和同步转速信息参与运算，因此在观测器观测到转子磁链信息后，还需要进行一系列计算，以得到预测控制需要的参数.

转子磁链信息包含转子磁链角度和转子磁链幅值，其中转子磁链角度 θ通常是通过对求反正切计算，为转子磁链角度观测值，为同步转速观测值，同步转速通过对转子磁链角度进行微分计算求得，磁链幅值即d轴磁链由 α轴和 β轴磁链平方和再开方计算.计算公式分别如式（27）～（29）所示.

其所对应的复矢量信号流图如图6 所示.

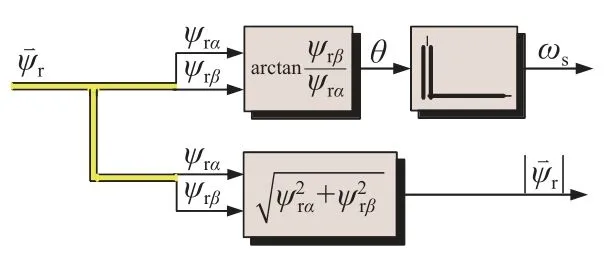
图6 同步转速与磁链幅值计算Fig.6 Synchronous speed and flux amplitude calculation

综上所述，感应电机速度自适应滑模观测器信号流图如图7 所示，图中第一部分是定子和转子部分组成的电流和磁链开环观测模型；第二部分是磁链观测补偿模型，根据滑模控制原理，由观测的定子电流与实际定子电流之间的偏差经过反馈增益矩阵对模型进行动态补偿调节，构成的闭环观测器模型；第三部分是速度自适应估计模型，通过定子电流偏差和转子磁链构成总的偏差信号，经过PI 控制器估计出转子转速的观测器模型.

图7 感应电机速度自适应滑模观测器Fig.7 Speed adaptive sliding mode observer for induction motor

3 实验验证

为了验证控制算法的准确性，在两电平逆变器交流调速平台上进行了实验验证.实验平台如图8(a)所示.主控芯片采用TI（德州仪器）C2000 系列中的TMS320F28379D 微处理器.控制器采样频率设置为20 kHz.感应电机参数为：额定功率Pn=2.2 kW，额定电压Un=380 V，额定电流In=4.94 A，额定转速ωn=1437 r·min-1，定子电阻Rs=2.7 Ω，转子电阻Rr=2.2 Ω，定子电感ls=0.316242038 H，转子电感lr=0.269745222 H，互感lm=0.257961783 H.感应电机无速度传感器预测控制系统信号流图如图8(b)所示.自适应滑模观测器的定子电压输入由预测控制算法输出的电压矢量号和母线电压重构得到.以电流模型计算的转子磁场角度为真实的转子磁场角度，实际电机转速由光电编码器测得.

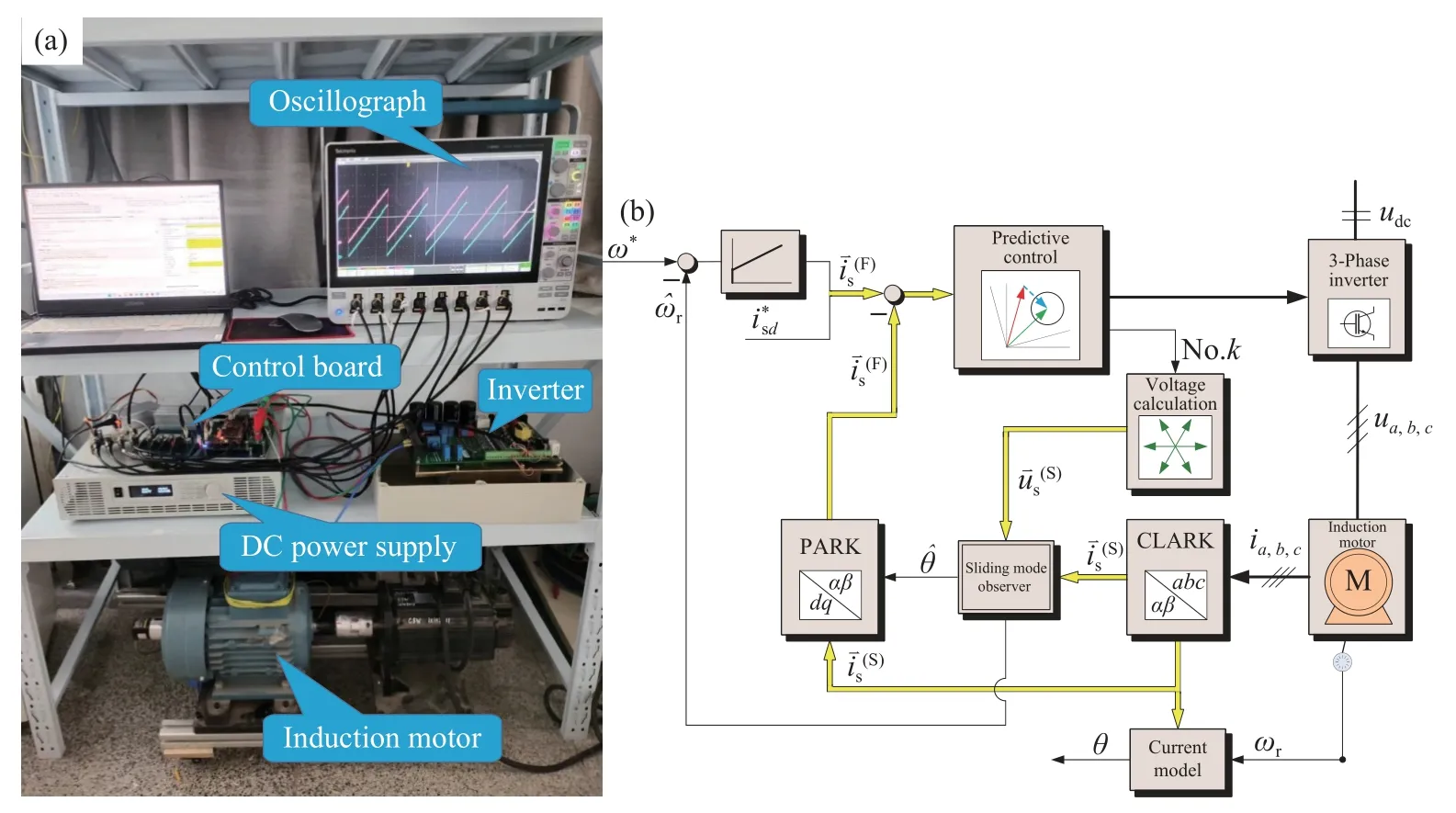
图8 感应电机控制系统对拖实验平台和无速度传感器预测控制系统信号流图.(a)实验平台;(b)信号流图Fig.8 Induction motor control system towing experiment platform and signal flow diagram of the speed sensorless predictive control system:(a) experiment platform;(b) signal flow diagram

3.1 稳态性能

图9(a)展示了运行在75 r·min-1转速下的实际速度 ωe、观测速度和速度观测误差 e_ωe.可以看到系统可以较为稳定运行在75 r·min-1转速下，基本维持在70～95 r·min-1之间.此时转速估测误差在-15～10 r·min-1之间波动.图9(b)展示了实际磁链角度 θ、观测磁角度和角度观测偏差e_θ.观测角度平直无弯曲，角度观测偏差维持在0.1～0.3 rad之间，最大相位差时间差为0.012 s.

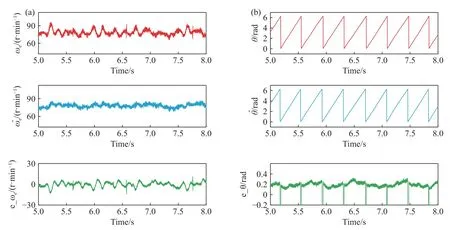
图9 75 r·min-1 转速下转子转速和磁链角度的实际值、观测值和观测偏差.(a) 转子转速;(b) 磁链角度Fig.9 Actual,observed,and observed deviations of rotor speed and flux angle at 75 r·min-1 speed: (a) rotor speed;(b) flux angle

图10(a)所示为高速时观测的电机转速、实际电机转速和观测偏差.高速时能实现转速的精确控制和转速的精确观测.速度可以精确控制在 ±5 r·min-1之间.转速观测偏差同样维持在较低水平，仅为±10 r·min-1.图10(b)为高速时观测的磁链角度实际的磁链角度和磁链角度观测误差，可以实现角度的精确观测，观测偏差维持在-0.09～-0.04 rad之间.最大相位时间差不到0.001 s.

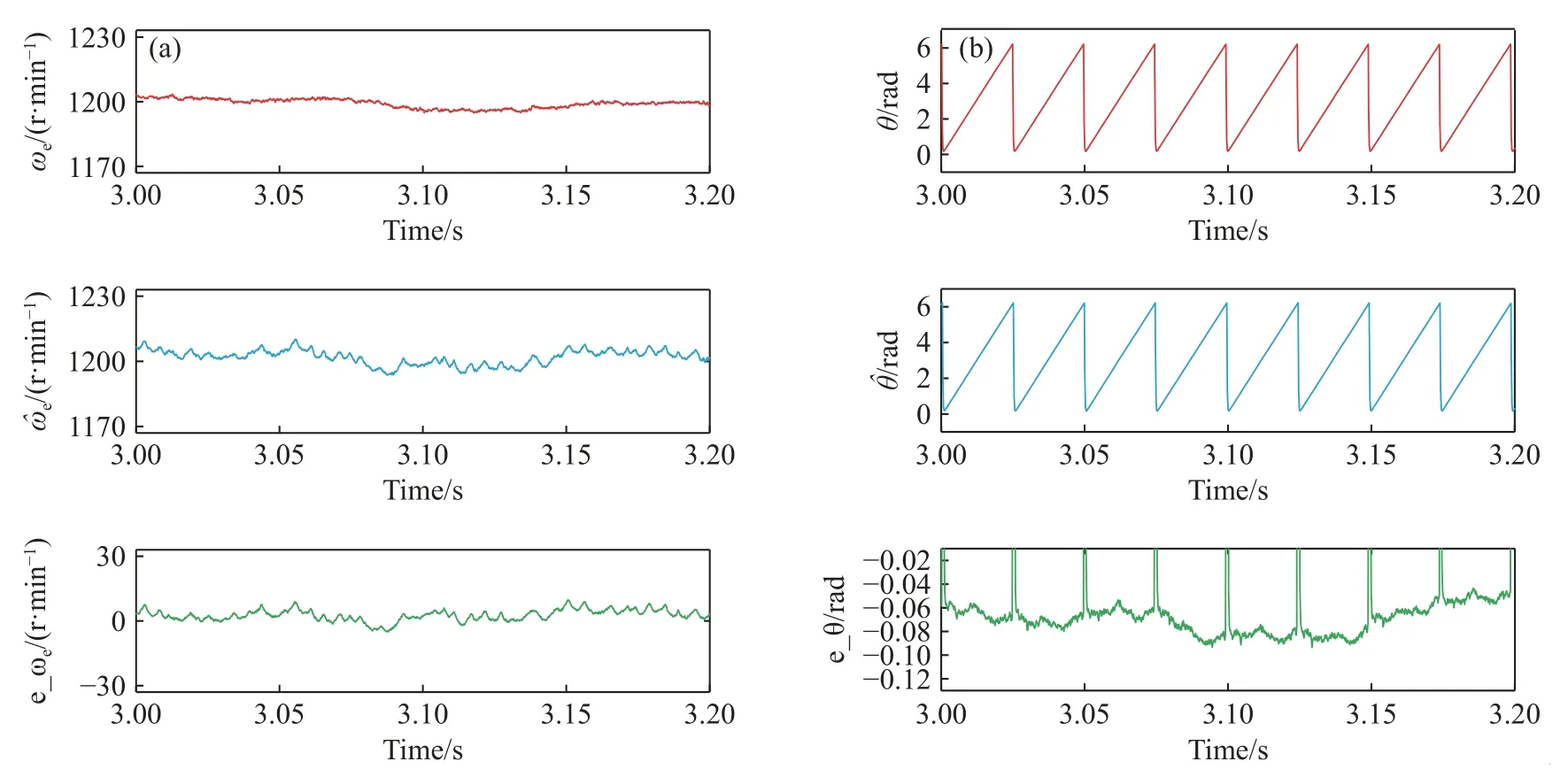
图10 1200 r·min-1 转速下转速和磁链角度的实际值、观测值和观测偏差.(a) 转子转速;(b) 磁链角度Fig.10 Actual,observed,and observed deviations of rotor speed and flux angle at 1200 r·min-1 speed: (a) rotor speed;(b) flux angle

图11 所示为控制系统的平均开关频率fsw，由1 s 内三相桥臂总的动作次数再除以3 计算得到.可以看出该无传感器预测控制系统的平均开关频率在510～460 Hz 之间波动，且在更小的时间尺度内，开关频率未发生大范围的波动，维持在非常低的水平.

图11 平均开关频率Fig.11 Average switching frequency

3.2 动态性能

图12(a)显示了电机转速由300 r·min-1突变到1200 r·min-1的实际转速观测转速和转速观测误差.可以看出在突然加速时速度可以迅速响应，经过约0.25 s 即达到目标转速，且只有较小的超调.由转速误差曲线可以看出在转速突变时观测器观测的转速与实际转速之间出现一定偏差，最大为220 r·min-1.不过观测偏差可以在0.25 s 以内迅速恢复到非常小的稳定值±8 r·min-1.调速时观测的磁链角度如图12(b)所示.图中红色曲线为实际磁链角度，蓝色曲线为观测磁链角度.可以看到动态过程中观测的磁链角度出现一定偏差，不过在0.3 s内又精确追踪到实际磁链角度.

图12 转速300～1200 r·min-1 动态过程中转速和磁链角度的实际值、观测值和观测偏差.(a) 转子转速;(b) 磁链角度Fig.12 Actual,observed,and observed deviations of rotor speed and flux angle during the 300-1200 r·min-1 speed dynamic process: (a) rotor speed;(b) flux angle

为了进一步分析速度突变时系统的动态响应过程.图13(a)展示了速度变时的d-q轴电流曲线.q轴电流迅速增加到最大限幅值7.0 A 以提供最大扭矩加速，电机转速迅速提升.随着转速的升高，观测的电机转速与参考电机转速之间的偏差逐渐减小，q轴电流随之逐渐减小并恢复稳定.选取1.806～1.847 s 之间d-q坐标系下的电流轨迹如图13(b)所示.1.831 s 时电流由M点迅速上升，经过两次转折即达到新的目标电流，瞬态过程中，d轴电流发生小范围过冲，但迅速回归到边界圆内.阶跃后，电流轨迹同样被很好的限制在绿色限定边界内，图中最大超出边界处为P点.

图13 转速300～1200 r·min-1 动态过程中的d-q 轴电流和电流轨迹.(a) d-q 轴电流;(b) d-q 轴电流轨迹Fig.13 d-q shaft current and current track in the 300-1200 r·min-1 speed dynamic process: (a) d-q shaft current;(b) d-q shaft current track

为了更直观地看到电机的电流情况，图14 展示该控制算法下电流传感器采集的A、B 两相电机相电流，分别表示为iA、iB，电机相电流频率稳定且与基频一致.

图14 转速1200 r·min-1 时相电流图Fig.14 Phase current at the speed of 1200 r·min-1

为测试控制系统快速过零的性能，进行了速度反转实验.图15(a)展示了速度由150 r·min-1突变到-150 r·min-1的动态过程.电机首先稳定运行在150 r·min-1转速下，在1.86 s 时给定-150 r·min-1的参考转速，电机迅速通过0，然后快速加速到目标转速-150 r·min-1，并逐渐稳定.可以看在快速反转时电机转速出现一定误差，在1.91 s 时达到最大值-75 r·min-1，但是可以随迅速减小，并最终维持在-7～15 r·min-1之间.速度快速反转时观测的磁链角度如图15(b)所示.观测的磁链角度在电机反转时实现平滑过渡.在快速反转时观测的磁链角度略微出现偏差.在1.864 s 速度接近0 时偏差逐渐增大，速度即将达到目标转速时达到最大值-0.91 rad，后迅速减小.经过0.25 s 实现角度的精确观测，最终稳定在-0.04～0.04 rad 之间.

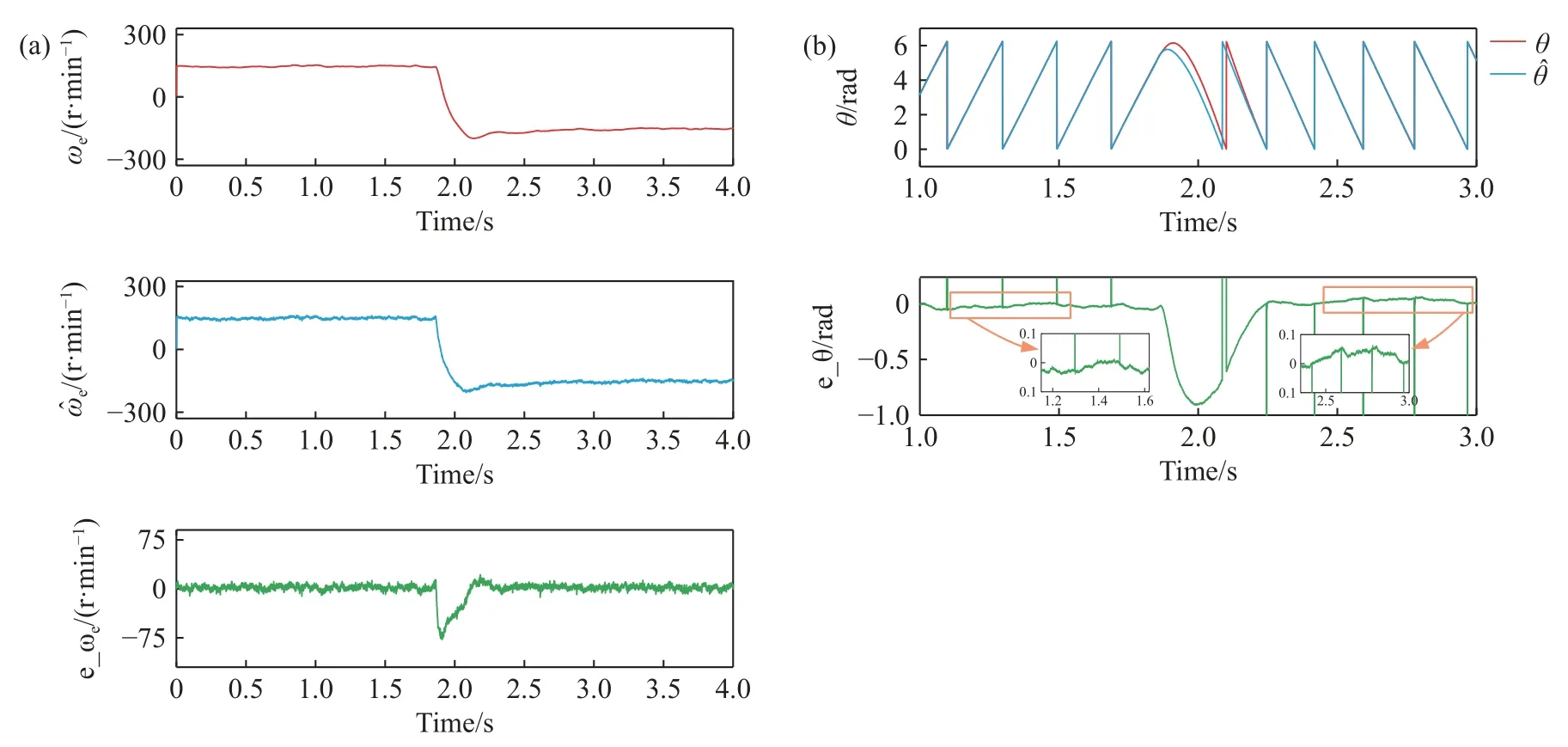
图15 转速-150～150 r·min-1 动态过程中转速和磁链角度的实际值、观测值和观测偏差.(a) 转子转速;(b) 磁链角度Fig.15 Actual,observed,and observed deviations of rotor speed and flux angle during -150-150 r·min-1 speed dynamic process: (a) rotor speed;(b) flux angle

4 结论

在传统低开关频率控制方法中，开关频率的降低会导致采样频率的下降，从而产生较大的时间延迟，这会对无感磁链观测带来不利影响.因此，本文提出了一种具有低开关频率的感应电机无传感器控制方法，使用速度自适应滑模观测器与电流预测型开关策略相结合，构成感应电机无传感器控制系统，可以在保持较高采样频率的前提下，有效降低开关频率，从而保证观测精度，使系统具有较高的动态及静态性能.主要结论有：

(1)提出的具有低开关频率的感应电机无传感器控制方法，可以将逆变器平均开关频率保持在较低的水平.实验测得，系统平均开关频率在500 Hz左右.

(2)将滑模控制思想与电流预测型开关策略相结合，无传感器控制方法具有良好的稳态性能，保证了系统在低开关频率下仍具有较高的观测精度和鲁棒性.实验验证，系统在稳态条件下，可以稳定运行在75 r·min-1转速下，转速估测误差在-7～15 r·min-1之间波动.

(3)使用电流预测型开关策略代替传统的低开关频率控制方法，无传感器控制方法具有较好的动态性能.直接电流控制的动态响应时间仅为1.52 ms，且在动态过程中，速度可以实现快速的过零，磁链幅值及角度均没有过多的抖动.所有动态过程中，速度都可以迅速响应，响应时间仅为0.25 s.动态响应前后，电流都被很好的限制在圆形边界内，转矩电流响应迅速且平滑.