情绪因素影响下的煤矿企业冲突管理演化博弈分析
2024-02-22肖雨晨
李 琰,肖雨晨
(西安科技大学 管理学院,陕西 西安 710054)
长期以来,煤矿行业的安全生产问题一直备受社会关注。2022年,全国矿山共发生事故367起,死亡518人,同比分别下降3.4%和2.4%[1]。随着主体安全责任的有效落实、监察执法力度的不断加大,煤矿行业安全生产工作取得了明显成效。影响煤矿安全生产的因素众多,人的不安全行为是事故频发的重要原因[2,3]。同时,煤矿安全生产涉及的各主体之间的相互作用关系也会影响事故的发生[4]。在作业过程中,矿工与管理者难免会由于心理认知差异[5]、情绪状况[6]、领导风格[7]等形成反对意见,不可避免地会产生冲突。在一定程度上,这些冲突会降低班组成员之间的信赖程度,抑制班组成员齐心完成安全生产目标的决心,从而影响企业的安全生产。但冲突不仅只会给组织带来消极影响,建设性的冲突处理方式也能给组织带来积极影响[8]。在煤矿企业中,及时地正向干预管理者和矿工之间的冲突,矿工的执行能力就会越强,该煤矿企业的应急管理水平就会越高,极大地降低了不安全事故发生的风险[9]。且班组内人际关系也会越和谐稳定,矿工和管理者对于安全生产的共同意愿加深,最终能够提高组织的安全生产绩效[10]。因此,冲突管理就显得尤为重要。
矿井的环境和工作内容十分特殊和复杂,对人的情绪消耗较为严重[11]。而情绪又是不安全行为的直接诱因,紧张、烦闷等不稳定情绪会提高不安全事故发生的概率[12],因此对矿工和管理者情绪的研究也已成为亟待解决的热点。现有研究[13,14]在冲突演化的过程中未能考虑到主体情绪因素的作用,具有一定的局限性。在现实中,人的情绪会引导其认知发展变化,显著影响自身面临冲突事件时的信息理解、判断和行为的选择[15]。实际的冲突过程中,考虑参与主体的行为决策或多或少会受到情绪这种非理性因素的影响。
由QUIGGIN[16]提出的等级依赖期望效用(RDEU)理论,能立足于冲突过程中决策者面对不确定条件时不同的情绪,构建不同情绪状态下的非线性决策权重,将非理性因素纳入行为决策的选择中。熊国强[17]基于RDEU理论构建非期望效用下博弈模型,为研究纳什均衡与博弈主体情绪因素之间的相关性奠定了基础。综上所述,本文通过建立包含情绪函数的RDEU非对称演化博弈模型,寻求在随机情绪组合下的均衡解,分析矿工和管理者在冲突过程中的决策特征,为有效治理冲突事件、促进煤矿安全生产提供理论依据和建议。
1 基于RDEU理论的冲突管理博弈模型构建
1.1 RDEU理论
等级期望效用理论(RDEU)是一种包含个体的心理偏好和情绪的效用理论,该理论视决策主体为不完全理性,通过“效用函数U(x)”和“决策权重函数π(x)”定义的实值函数V来表示决策主体对策略的偏好,即:
式中,对于策略集合X={xi;i=1,2,…,n},参与者以概率P{X=xi}=pi对策略xi排序,并规定x1>x2>…>xn。定义策略xi的效用等级为Rpi:
Rpi=P{X≤xi}=pt+pt+1
(2)
该策略xi的概率分布函数即为Rpi。此外,
π(xi)=w(pi+1-Rpi)-w(1-Rpi)
(3)
w(·)为情绪函数,pi是该决策的客观概率。在情绪因素影响下,主观概率函数满足w(pi)=piri,ri为情绪指数,且ri>0[18]。当ri<1时,w(pi)为悲观情绪函数;当ri>1时,w(pi)为乐观情绪函数;当ri=1时,w(pi)为无情绪函数。RDEU理论引入行为策略的等级分布函数和情绪函数构成累积非线性决策权重,通过这种非线性的决策概率,探究冲突事件下,矿工和管理者的情绪状态对行为策略的作用。
1.2 模型假设
在对煤矿企业的冲突研究中,导致冲突产生的影响因素是多方面的。由于班组成员的异质性和多样性,使得矿工在日常的作业过程中由于学识背景、价值观念和利益诉求等差异与管理者产生意见或决策的分歧成为必然[19]。此外,随着煤矿企业供给侧改革的深入,部分煤矿企业内部的转型升级暴露出的管理体制和观念问题,不可避免地会使矿工产生不支持、不认同的消极心理,加大与管理者发生冲突的可能性[20]。
据此假设因煤矿企业改革而规定的绩效考核制度遭到了矿工的反对。传统煤矿企业本身发展历史久远,矿工的年龄较大且部分工作难以量化,不认可将上级主观性较强的评判作为绩效考核的结果,冲突由此展开。其中,涉及矿工和管理者两类博弈主体,并提出博弈模型的假设如下:
1)在发生冲突事件时,假设矿工的策略集为{对抗、缓和},管理者的策略集为{压制、让步}。且矿工采取“对抗”策略的概率为p,管理者采取“压制”策略的概率为q。在博弈过程中,引入双方情绪函数w(p)=pr1、w(q)=qr2,其中r1、r2分别为矿工和管理者的情绪指数,且满足r1>0,r2>0。
2)在双方博弈的过程中,矿工采取“对抗”策略会为自身争夺到V1的利益,管理者采取“压制”策略会为自身争夺到V2的利益,但此种抗争行为也会产生一定的安全风险S。当矿工和管理者都抗争时,矿工承担风险的比例为a,管理者承担风险的比例为1-a;当矿工对抗、管理者缓和冲突时,双方承担折扣因子为m的风险成本,且矿工和管理者承担的风险比例分别为b、1-b;当矿工缓和冲突、管理者压制时,双方承担折扣因子为n的风险,矿工承担风险的比例为c,管理者承担风险的比例为1-c。
3)矿工对抗的同时,管理者进行压制,会加剧双方的冲突,使得发生安全事故的风险更大。根据现实情况,当矿工和管理者都选择对抗时的收益比双方退让一步时小。故得到如下的收益大小关系:对矿工而言,V1-mbS>-C1>-C1-ncS>V1-aS。对于管理者而言,V2-n(1-c)S>-C2>-C2-m(1-b)S>V2-(1-a)S。于是,构建博弈演化收益矩阵见表1。

表1 矿工与管理者的收益矩阵Table 1 Revenue matrix of miners and managers
1.3 矿工冲突管理的RDEU博弈模型
根据RDEU相关理论以及模型基本假设,建立了矿工和管理者博弈双方的策略收益、概率、效用等级和决策权重,分别见表2和表3。

表2 矿工各策略对应的概率分布、秩及决策权重Table 2 The probability distribution,rank and decision weight of each miners’ strategy

表3 管理者各策略对应的概率分布、秩及决策权重Table 3 The probability distribution,rank and decision weight of each managers’ strategy
于是,矿工对应的RDEU期望效用函数为:
Up=(V1-mbS+C1)(p-pq)r1+ncS(1-q)r1+
(aS-C1-ncS-V1)(1-pq)r1+V1-a
(4)
管理者对应的RDEU期望效用函数为:
Uq=(V2-nS+ncS+C2)(q-pq)r2+(mS-mbS)(1-p)r2+
(-C2-mS+mbS-V2+S-aS)(1-pq)r2+V2-S+aS
(5)
2 矿工冲突管理的RDEU博弈模型演化均衡解
根据纳什均衡求解的基本方法,当矿工和管理者双方都采用混合策略,即p、q∈(0,1)时,将矿工和管理者的RDEU期望效用函数分别对p、q求偏导,可得:
r1(q-1)(p-pq)r1-1(C1+V1-mbS)
(6)
r2(p-1)(q-pq)r2-1(C2+V2-nS+ncS)
(7)
令A=C1+V1-mbS,B=C1+V1-aS+ncS,D=C2+V2-nS+ncS,E=C2-S+V2+aS+mS-mbS,其中A>0,B<0,D>0,E<0。
且令偏导为0,得到冲突管理RDEU博弈模型的纳什均衡解满足的条件:
A(p)r1-1(1-q)r1+Bq(1-pq)r1-1=0
(8)
D(q)r2-1(1-p)r2+Ep(1-pq)r2-1=0
(9)
对该组方程组求解需要对情绪指数进行分类讨论。因此,本文就博弈双方情绪状态表现为“双方均理性”、“仅有一方理性”和“双方均非理性”三种情况进行讨论。
2.1 双方均为理性状态
当矿工和管理者都处于理性状态时,r1=r2=1。将其代入式(8)、式(9)中可得矿工和管理者的混合策略均衡解为:
在现实情况下,受主客观诸多因素的影响,博弈参与双方容易带有非理性情绪,故理性状态下的冲突博弈在现实中较难出现。
2.2 一方为理性状态,另一方受情绪影响
在实际情况下,由于管理者掌握充足的信息资源和一定社会资源,是企业的规则制定者与打破者,在冲突事件中更易于保持理性思维。因此,将管理者假设为理性博弈主体,其行为符合有限理性假设,即r2=1。而相较之下,矿工处于被动地位,获取的信息资源不对称,当实际收益与理想需求条件不符时会产生非理性情绪,从而影响其行为决策,即r1≠1。参考RDEU冲突博弈模型中情绪函数的特征,将矿工带有的情绪分为“乐观”和“悲观”两种来分析。

根据此混合策略的纳什均衡解可知,当管理者处于理性状态、矿工处于乐观状态时,管理者的最佳策略选择为“让步”,通过协商的方式调解双方冲突,与矿工和解,而矿工却会在一定程度上选择“对抗”策略。因此,在应对冲突事件时管理者应该注重信息的公开与传递,在规划工作、制定决策时鼓励矿工积极参与,对潜在的冲突及时与矿工进行协商,综合矿工可能出现的“缓和”态度,采取最优的解决措施。

根据此混合策略的纳什均衡解可知,当管理者处于理性状态、矿工处于悲观状态时,管理者不会一度倾向于“让步”策略,而会在一定程度上选择“压制”的策略,从而使得矿工缓和冲突,逐步退让。当矿工极度悲观时,由于他们获取的相关信息相较闭塞、需求未能得到满足、认知较为片面等,可能使其对冲突事件的认识主观、越发激进。此种情况下,管理者会选择一定比例的“压制”策略来面对极度悲观的矿工群体。
2.3 双方均受情绪影响
矿工和管理者双方都受到情绪的影响,做出非理性的决策,此时r1≠1,r2≠1。矿工与管理者的反应函数分别如下:
为了分析情绪指数的变化对于博弈方行为决策的影响,将p、q分别看作r1、r2的函数,并记为p(r1)、q(r2)。通过对p(r1)、q(r2)求导,根据其一阶导数观察情绪指数r1、r2对p、q的影响。
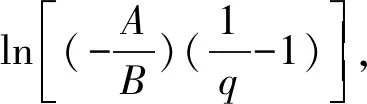
2)当q>A/(A-B)时,p′(r1)<0在(0,1)和(1,+∞)上恒成立,则p(r1)为r1的减函数。反映出当管理者采取“压制”策略的概率大于A/(A-B)时,若矿工处于乐观的情绪,随着情绪指数r1增大,选择“对抗”的行为策略概率会减小,期望通过妥协的态度来化解冲突。但若矿工处于悲观的情绪中,会趋于选择“对抗”的策略。当管理者对矿工的对抗行为采取压制的态度时,由于矿工处于乐观情绪,考虑到自身进一步对抗时付出的人力和物力等成本,因此会转而退让。当矿工处于悲观情绪时,相信管理者为了维护己方利益而不断地进行压制,会产生“破窗效应”,坚持与管理者抗争到底。
3)当q=A/(A-B)时,p′(r1)=0在(0,1)和(1,+∞)上恒成立,则p(r1)的变化与r1无关。当管理者以q=A/(A-B)的固定概率做出决策时,矿工会相应地采取一定的行动,其策略选择不受情绪影响,而此种情况与实际不符。
同样地,对式(13)进行分析,可知故q′(r2)的正负取决于p和D/(D-E)的大小关系。下面分情况予以讨论:
1)当p
2)当p>D/(D-E)时,q′(r2)<0在(0,1)和(1,+∞)上恒成立,则q(r2)为r2的减函数。反映出当矿工采取“对抗”策略的概率大于D/(D-E)时,若管理者处于乐观的情绪,随着情绪指数r2增大,选择“压制”的行为策略概率会减小,期望通过与矿工的和平对话来化解争端。但若管理者处于悲观的情绪中,会不断推进对矿工的“压制”策略。
3)当p=D/(D-E)时,q′(r2)=0在(0,1)和(1,+∞)上恒成立,则q(r2)的变化与r2无关。p=D/(D-E)的固定概率是影响矿工行为决策的临界点,此时,管理者会相应地对自身决策进行调整,而与情绪变化无关,但此种情况与实际不符。
3 数值模拟
基于前文博弈模型的建立和求解分析,为了观察不同情绪对博弈双方决策行为的影响,以验证模型的性质与适用性,利用MATLAB软件进行数值模拟仿真。根据前文假设条件,设定模型的具体数值为:C1=0.5,V1=1,C2=0.6,V2=1.2,S=6,a=0.5,m=0.2,b=0.55,n=0.2,c=0.45,易得A=0.84,B=-0.96,D=1.14,E=-0.66。则双方均为理性状态时混合策略均衡解为:
根据现实情况,双方均为理性状态非常少见。下面通过MATLAB软件对博弈双方均带有情绪时的行为决策进行三维图像描述。
1)矿工受自身情绪和对方行为策略影响的情况。矿工在悲观情绪中受管理者决策影响的三维示意如图1所示,当r1∈(0,1),即矿工处于悲观情绪中,一旦认为管理者选择“压制”策略的概率q小于0.47时,随着r1的不断增加,其选择“对抗”的概率p也不断增加。反之,当矿工认为管理者选择“压制”策略的概率大于0.47时,随情绪指数r1的增加,矿工选择“对抗”策略的概率会逐渐下降。并且q越大,p下降幅度越大。
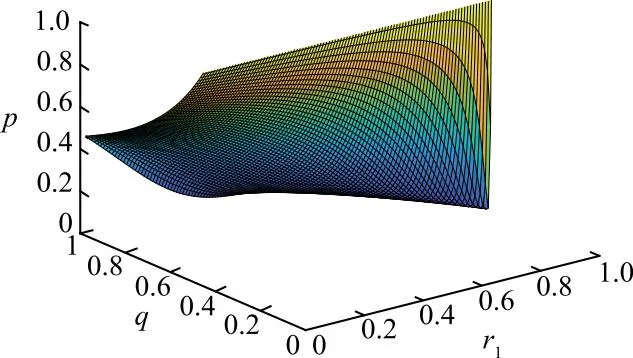
图1 矿工在悲观情绪中受管理者决策影响的三维示意Fig.1 Three-dimensional diagram of miners affected by managers’ decisions in a pessimistic mood
而当r1∈(1,5)时,即矿工处于乐观情绪中,如图2所示,当q小于0.47时,p随r1的增大而增大,且增加的幅度较大;当q大于0.47时,p随r1的增大而减小。矿工认为管理者选择“压制”策略的概率较小时,随情绪越来越乐观,更倾向于选择“对抗”策略以争取更多利益,而当他们认为管理者选择“压制”策略的概率较大时,乐观状态下的矿工会考虑缓和对抗,通过让步来避免遭受损失。
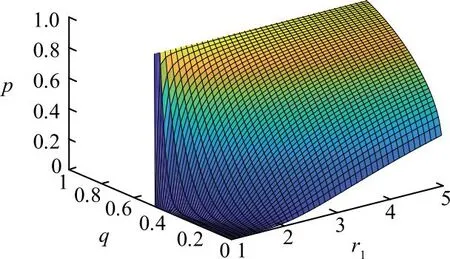
图2 矿工在乐观情绪中受管理者决策影响的三维示意Fig.2 Three-dimensional diagram of miners affected by managers’ decisions in an optimistic mood
2)管理者受自身情绪与对方行为策略影响的情况,如图3所示,当r2∈(0,1),即管理者处于悲观情绪中,管理者认为矿工选择“对抗”策略的概率p<0.63时,随着r2的不断增加,其选择“压制”的概率q会不断增加。而当矿工选择“对抗”策略的概率p>0.63,管理者情绪指数r2越小,即越悲观情绪,此时很大程度上会坚持“压制”策略。同样地,当r2∈(1,5)时,即管理者处于乐观情绪中,如图4所示,当p<0.63时,q随r2的增大而增大,且增加幅度大;当p>0.63时,q随r2的增大而减小。
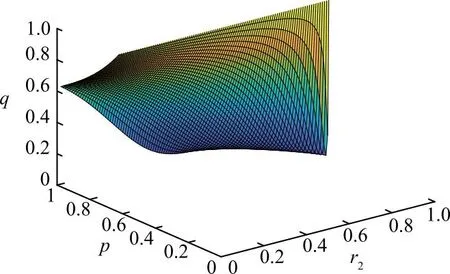
图3 管理者在悲观情绪中受矿工决策影响的三维示意图Fig.3 Three-dimensional diagram of managers affected by miners’ decisions in a pessimistic mood
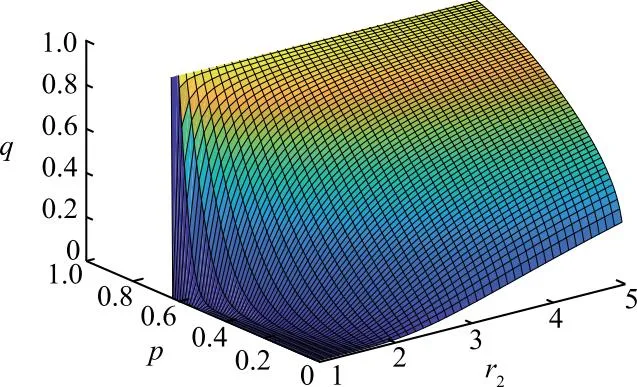
图4 管理者在乐观情绪中受矿工决策影响的三维示意Fig.4 Three-dimensional diagram of managers affected by miners’ decisions in an optimistic mood
4 结论与建议
4.1 结 论
情绪对冲突事件博弈主体的策略选择影响显著,矿工和管理者的非理性情绪不利于有效处理冲突问题。总的来说,对于矿工和管理者而言,当其处于悲观情绪时会偏向于采取“对抗”的强硬行为表达诉求,争取更多的利益;而当其处于乐观情绪时,提高了和平解决冲突的概率,倾向于选择“缓和”或“让步”的保守行为策略。此外,矿工和管理者采取何种方式应对冲突事件还取决于其对另一方策略选择的判断。当博弈主体认为对方选择抗争行为的概率小于某一阈值时,所处的乐观情绪会使其采取抗争性策略的概率越来越大,以争取最多的利益。反过来,当博弈主体认为对方选择抗争行为的概率大于某一阈值时,受悲观情绪影响,其选择抗争行为的概率也会减少。
4.2 建 议
1)重视矿工群体诉求,促进信息顺畅流通。管理者应该积极地了解矿工各个阶段的心声与诉求,结合企业的实际情况尽力满足员工的基本需求。此外,管理人员也需要加强与矿工之间的信息交流,对于作业过程中的重要信息及时上传下达,弱化信息不对称可能带来的双方认知偏差,这样就可以为作业中双方行为决策做出科学合理的判断提供充分的参考依据。
2)加强风险情绪监测,干预疏导消极情绪。在管理过程中应注重矿工的情绪波动,加强对矿工的风险情绪监测。管理人员应定时下沉到作业现场,去基层观察与感受,对部分矿工出现的消极情绪及时进行心理疏导,加强人文关怀,提供科学、合理的心理教育,让矿工正当地提出其诉求并予以解决,有效缓解冲突事件升级与恶化。
