一种适合太赫兹通信的新波形方案：GFB-OFDM

辛 雨,华 健,胡留军,段向阳,3

(1.移动网络和移动多媒体技术国家重点实验室,广东 深圳 518055;2.中兴通讯股份有限公司,广东 深圳 518057;3.北京邮电大学,北京 100876)

0 引言

太赫兹技术是一种新型频谱技术[1-2],也称为“改变未来世界的十大技术之一”,它可以提供更大的传输带宽,满足更高速率的传输需求,逐渐成为6G通信技术研究的重要组成部分。

太赫兹通信通常是指利用频率0.1～ 10 THz、波长3 mm～30 μm的电磁波进行通信的技术[3]。太赫兹通信主要有以下特点：① 超大带宽,太赫兹通信的带宽可以达到几GHz至几十GHz;② 超高速率,峰值速率可以达到1 Tbit/s[4];③ 穿透性强[5]、能量低、时间分辨率高和保密性好等。

太赫兹通信中,超大带宽的实现具有一定的挑战性。由于硬件成本和实现复杂度等因素的影响,目前3GPP协议中的正交频分复用(Orthogonal Frequency Division Multiplex,OFDM)使用支持的最大子载波间隔和最大快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)点数不足以满足太赫兹场景超大带宽的需求,即最大子载波间隔960 kHz和最大IFFT点数4 096只能实现4 GHz左右的带宽。若想支持更大的带宽,通常从两个方向去调整：增大子载波间隔和增大IFFT点数。增大子载波间隔意味着符号长度变短,循环前缀(Cyclic Prefix ,CP)占比增大,频谱效率和传输速率降低。增大IFFT点数对于现有硬件来说难以支持,复杂度也会提高,通常P点IFFT的复杂度为PlbP[6]。本文通过调整波形方案,实现超大带宽的太赫兹通信。

现有5G标准中使用的波形主要为循环前缀正交频分复用 (Cyclic Prefix Orthogonal Frequency Division Multiplexing,CP-OFDM)和基于离散傅里叶变换的扩频正交频分复用 (Discrete Fourier Transform Spread Orthogonal Frequency Division Multiplexing, DFT-s-OFDM)。近年来,关于波形的研究也有很多[7],基于OFDM提出的新波形方案主要有：① 滤波器组多载波(Filter Bank Multi Carrier,FBMC)[8]是一种实数调制,它将已调信号的实部和虚部分离,利用滤波器实现正交特性;② 广义频分复用 (Generalized Frequency Division Multiplexing,GFDM)[9-10]采用循环滤波器对每个OFDM子载波都进行滤波;③ 滤波器组正交频分复用 (Filter Bank Orthogonal Frequency Division Multiplexing,FB-OFDM)[11-13]利用多相滤波器对每个子载波进行滤波,子载波间近似正交;④ 通用滤波多载波 (Universal Filtered Multi-Carrier,UFMC)[14],该波形对每组连续的子载波分别进行滤波操作;⑤ 滤波正交频分复用 (Filter Orthogonal Frequency Division Multiplexing, F-OFDM)[15],该波形对整个子带进行滤波操作;⑥ 正交时频空调制 (Orthogonal Time Frequency Space, OTFS)[16]是一种基于在时延-多普勒域调制数据的波形。以上这些波形方案都不能很好地支持超大带宽通信需求。

提出了一种新的波形技术：广义滤波器组-正交频分复用(Generalized Filter Bank Orthogonal Frequency Division Multiplexing, GFB-OFDM)技术,它是一种利用两级IFFT和多相滤波器来实现多子带联合处理的波形方案,可以将大点数IFFT分解成两级小点数的IFFT,实现更大的IFFT点数操作[17]。GFB-OFDM可以灵活地配置子带数、子带内子载波数、子载波间隔、滤波器参数等系统参数,满足太赫兹通信系统的各种应用场景需求。

1 GFB-OFDM波形收发处理过程

1.1 GFB-OFDM发送端系统

GFB-OFDM发送端系统框架如图1所示,首先获取待发送的编码调制后的数据,将其进行子带划分,分成多组数据,对每个子带的数据进行一级IFFT变换,也称为子载波级IFFT,子载波级IFFT点数与子带内的子载波数有关;然后对每个子带的 一级IFFT后的数据联合进行二级IFFT变换处理,也称为子带级IFFT,子带级IFFT点数与子带个数有关,再通过加窗或其他操作进行多相滤波处理;最后经过数字模拟转换器 (Digital-to-Analog Converter,DAC)模块和射频 (Radio Frequency,RF)模块变换,即可发送数据。其中,子带划分处理以及子带内进行一级IFFT变换称为子载波级处理模块, 二级IFFT变换和多相滤波模块称为子带级处理模块。

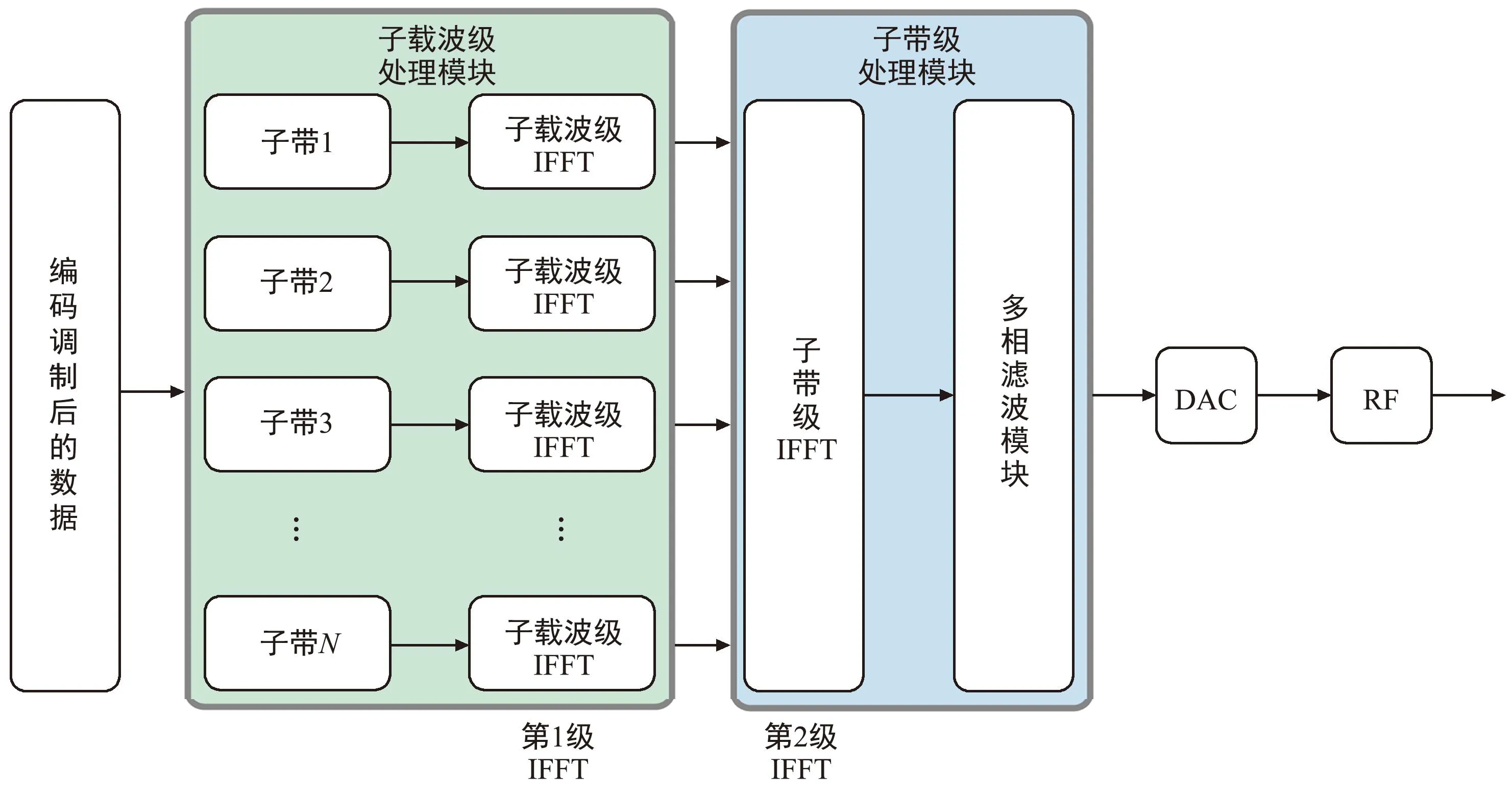
图1 GFB-OFDM的发送端系统框图Fig.1 GFB-OFDM transmitter system block diagram

经过上述两级IFFT模块的处理,可以将大点数的IFFT拆解成两级小点数的IFFT,这样可以解决硬件实现困难及处理复杂度的问题。

1.2 发送端数据处理过程

按照传统的CP-OFDM传输8 192个子载波的频域数据,通常至少需要做Nifft=16 384点的IFFT来实现。而对于GFB-OFDM而言,处理过程会简单很多。

如图2所示,有8 192个经过编码调制后的待传数据(8 192个子载波的频域数据),将待传数据分成N组(在本例中,N=8,即8个子带),其中每个子带含有M个数据,M=1 024,可以分别表示为：X[m,n],m=1,2,…,1 024,n=1,2,…,8。

图2 GFB-OFDM的数据处理过程Fig.2 GFB-OFDM data processing process

对每个子带的数据分别进行IFFT(一级IFFT)得到8个子带的时域数据x[i,n],如式(1)所示,其中i=1,2,…,1 024,为IFFT后的时域数据序号。

(1)

令A为傅里叶逆变换矩阵,则式(1)写成矩阵的形式：

(2)

对8个子带的时域数据分别添加CP的操作,得到：

(3)

式中：Ncp为CP的长度,通常为符号长度的1/16,令Ncp=64。

每次按顺序分别对8组时域数据x(Ncp+M)×N提取一个数据,共8个数据,进行N2点的两倍过采样IFFT(二级IFFT),N2为二级IFFT点数且有N2=Nifft/M=16,共进行Ncp+M次二级IFFT,得到Ncp+M组数据,每组包含16个数据,每组数据为一个子符号数据,写成矩阵的形式有：

(4)

式中：B为傅里叶逆变换矩阵,YN2×(Ncp+M)为进行二级IFFT的数据矩阵。

(5)

式中：Ns为过采样时的单侧补零量。对每组数据进行重复L次的操作(在本例中,L=4),再与滤波器函数进行点乘操作(多相滤波操作),得到新的Ncp+M组数据,每组包含64个数据,写成矩阵的形式：

(6)

z4N2×(Ncp+M)=y4N2×(Ncp+M)·[g(ts);g(ts);…;g(ts)],

(7)

式中：“·”为点乘操作,列向量g(ts)为多相滤波函数,是函数g(t)的离散形式,其中g(t)是双根升余弦函数的时域形式。向量长度为4N2,重复Ncp+M次得到4N2×Ncp+M的滤波矩阵。

在时域上将Ncp+M组数据进行错位叠加的操作,错位长度为一个子符号长度,即16个数据长度,如图2所示。最终在时域上发送一组叠加后的时域数据。

上述过程看出,GFB-OFDM可利用8个1 024点的一级IFFT和1 024个16点的二级IFFT完成 16 384点的IFFT,实现了用两级小点数IFFT完成一级大点数IFFT。同理,也可以将8 192个子载波分成16个子带,每个子带包含512个子载波,GFB-OFDM利用16个512点的一级IFFT和512个32点的二级IFFT完成16 384点的IFFT,具体过程在此不一一叙述。

1.3 多相滤波的滤波函数

多相滤波操作中滤波函数的参数对整体GFB-OFDM的性能有一定的影响,所以需要选择一个合适的滤波函数[18-19]。

双根升余弦滤波函数是一种利用时域根升余弦函数对频域根升余弦函数的时域形式数据进行加窗截取的滤波函数。

频域根升余弦函数的时域形式可以表示为：

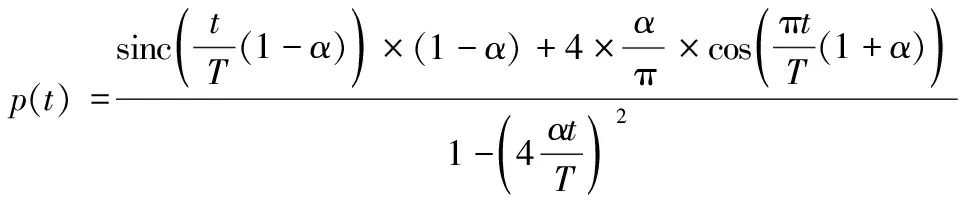
(8)

式中：α为根升余弦函数的滚降系数,T为1.2节中的子符号长度。

时域根升余弦函数表达式如式(9)所示,其中,β为根升余弦函数的滚降系数,Tb为时域升余弦函数在时域上的半幅宽度的1/2。因此该时域升余弦函数的时域长度为2Tb×(1+β)。

(9)

则双根升余弦函数DRRC时域形式g(t)表示为：

g(t)=q(t)p(t)。

(10)

滤波函数的时域长度和每组子符号重复L次后的长度相等,即2Tb×(1+β)=LT。

1.4 接收端处理

接收端按照传统CP-OFDM的接收方法,如图3所示。接收端对接收到的多个OFDM符号的时域数据分别进行去CP操作,随后进行FFT得到子载波数据,再进行频域信道均衡、解调译码等操作,最终得到比特信息。经过上述过程可以无损地接收到发送端的比特信息。

图3 接收端处理过程Fig.3 Processing at the receiving end

1.5 GFB-OFDM波形的优点

GFB-OFDM利用两级IFFT可以将原有的大点数IFFT分解成两级小点数的IFFT,以实现更大的IFFT点数操作。除了这个优点之外,GFB-OFDM波形方案还具备以下优点：

① 在子带带宽不变的情况下,通过调整子带数量就可以实现不同信道带宽的数据传输,这有利于在某些硬件不变的情况下灵活支持不同的信道带宽需求。

② GFB-OFDM的多相滤波操作相当于是对每个子带进行了滤波操作,可以减少子带间的带外泄露,因此可以支持不同子带间灵活使用不同子载波间隔的场景需求,并且这些不同子载波间隔的不同子带可以统一进行GFB-OFDM波形处理。

③ 不同子带内的数据可以为不同类型的数据,既可以是多载波数据也可以是单载波数据,GFB-OFDM的子带级处理模块可以对不同数据类型的子带一起进行处理,以实现单载波和多载波的融合处理。

④ 接收端按照现有的5G NR中OFDM的接收方法处理,并不会带来额外的接收复杂度。

2 GFB-OFDM波形性能仿真分析

GFB-OFDM波形与5G NR的CP-OFDM波形的性能仿真对比及分析。表1为仿真参数,在本仿真中假设CP-OFDM波形可以支持16 384点数的IFFT(两倍过采样IFFT)。

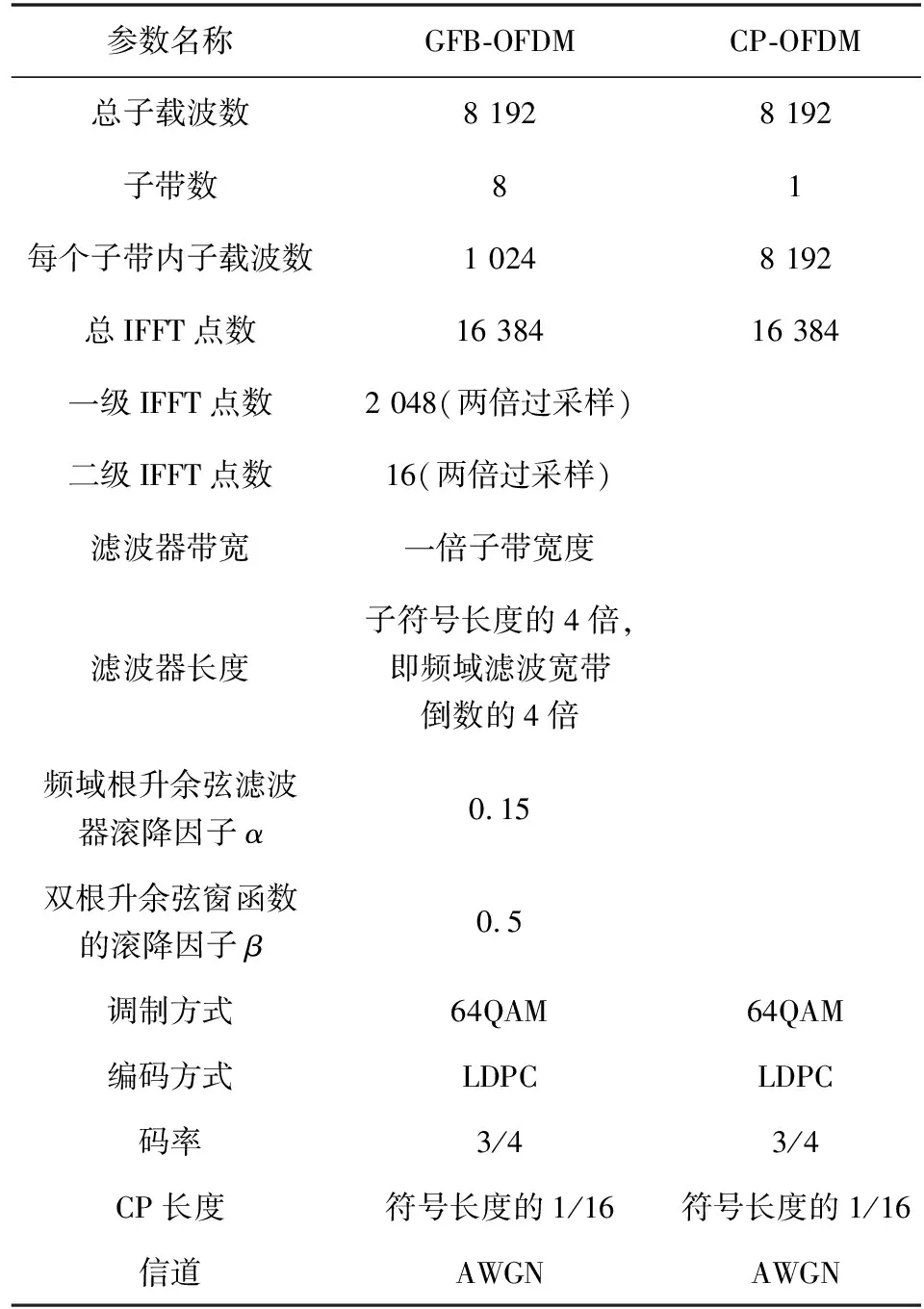
表1 仿真参数Tab.1 Simulation parameters

2.1 带外泄露

CP-OFDM和GFB-OFDM的功率谱密度(Power Spectral Density,PSD)如图4所示。由于GFB-OFDM使用了多相滤波操作,因此带外泄露会比较低,由图4可以看出,GFB-OFDM的带外泄露明显低于CP-OFDM,因此可以减少保护带宽,提高频谱效率。

图4 CP-OFDM和GFB-OFDM的带外泄露对比Fig.4 Comparison of out-of-band leakage between CP-OFDM and GFB-OFDM

2.2 相同子载波间隔场景的误块率性能

在表1给出的仿真参数下,假设信道带宽中的所有子载波间隔相同,并设子载波间隔为480 kHz。为了减少GFB-OFDM中子带间的干扰,一级IFFT也采用两倍过采样,即通过补零的方式使用 2 048点IFFT。接收端采用传统的CP-OFDM的接收算法,图5给出了CP-OFDM和GFB-OFDM的误块率(Block Error Rate,BLER)性能仿真结果,可以看出,这两种波形的BLER性能相同。这验证了GFB-OFDM的BLER性能没有损失。

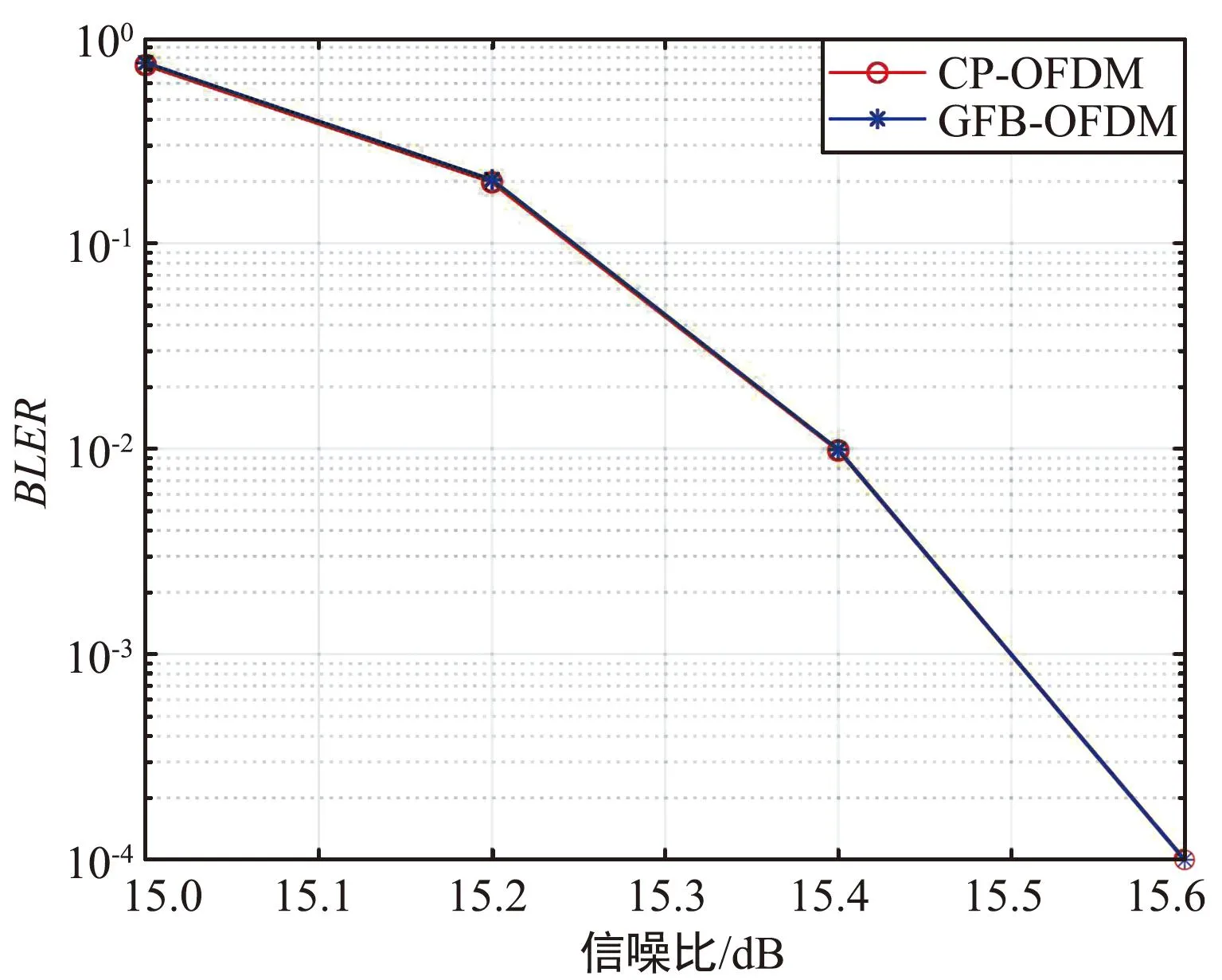
图5 相同子载波间隔场景的BLER性能Fig.5 BLER performance for the same subcarrier interval scenarios

2.3 不同子载波间隔场景的BLER性能

在表1给出的仿真参数下,假设信道带宽中的子载波间隔存在不同,如图6所示的不同子载波间隔子带共存的情况,其中子带4的子载波间隔为960 kHz,其余子带的子载波间隔为480 kHz。传统CP-OFDM无法将不同子带的数据一起进行IFFT处理,而本文提出的GFB-OFDM方案可以将所有子带一起处理,体现了该波形方案针对不同需求的灵活性,具体过程如图7所示,将子带4相邻两个符号的一级IFFT之后的数据分别添加CP之后串联,然后与其他子带的数据一起进行二级IFFT,其他处理不变。

图6 频域8个子带的位置Fig.6 Locations of the 8 subbands in the frequency domain

图7 不同子载波间隔的子带数据处理过程Fig.7 Subband data processing procedure for different subcarrier intervals

图7的仿真中,CP-OFDM波形对480 KHz子载波间隔的数据和960 KHz子载波间隔的数据分别采用16 384点数的过采样IFFT操作,然后将两个时域数据进行叠加形成一组时域数据。

图8给出了接收端对子带4传输的数据进行解调的BLER性能对比,由于子带4会受到其他不同子载波间隔子带的干扰,因此BLER性能会有所下降。由图8可以看出,GFB-OFDM的性能比CP-OFDM要好,主要是因为GFB-OFDM发送端有多相滤波的作用,使得每个子带的带外泄露都很低,所以子带间干扰要小于CP-OFDM的子带间干扰,BLER性能比CP-OFDM要好,因此GFB-OFDM在不同子载波间隔场景时,会有一定的优势。

图8 不同子载波间隔场景的BLER性能Fig.8 BLER performance for different subcarrier interval scenarios

2.4 复杂度分析

GFB-OFDM相对于CP-OFDM而言,处理复杂度会更低,具体原因如下：

① CP-OFDM不同子载波间隔的子带不能一起做IFFT,需要分开单独处理,然后在时域上叠加,这样处理复杂度很高。特别是当需要分开单独处理的子带个数增加时,会明显增加处理复杂度。

② GFB-OFDM中,不同子载波间隔的子带可以统一处理,而且子带划分会很灵活。在相同带宽下,改变子带划分的大小及增加子带个数,不会增加处理复杂度。

3 结束语

介绍了一种适合太赫兹通信场景的新波形方案——GFB-OFDM,该波形方案采用两级小点数IFFT和多相滤波操作,实现大点数IFFT效果,支持大信道带宽通信场景;子带带宽不变的情况下,通过调整子带数量实现不同信道带宽的数据传输,有利于在某些硬件不变的情况下灵活支持不同的信道带宽需求;支持信道带宽内子载波间隔灵活变化的场景需求及支持单载波和多载波的融合处理需求,且没有增加处理复杂度。通过理论分析和仿真验证,GFB-OFDM在太赫兹超大带宽通信场景及不同子载波间隔需求场景下具有一定的优势。

未来6G太赫兹通信将覆盖很多复杂的应用场景,不同应用场景的需求在多个性能指标上也会有所不同。GFB-OFDM可以根据场景的改变和需求,支持和实现超大带宽、超高速率、不同数据类型、不同子载波间隔、不同信道带宽等参数的特殊需求。