穿越煤系地层隧道预留岩墙破坏力学行为与安全厚度研究
2024-02-21许煜林邸小勇李哲宇杨红运
许煜林, 邸小勇, 巩 雯, 林 志, 李哲宇, 杨红运
(1. 重庆交通大学 山区桥梁及隧道工程国家重点实验室, 重庆 400074;2. 重庆高速工程顾问有限公司, 重庆 404100)
0 引言
我国经济快速发展,公路隧道的数量随着公路里程的增加在逐年增加,2022年公路的总里程相对于2021年同比增长了1.38%,2019年隧道数量相对于2018年同比增加了6.80%。我国很多地区地形地貌复杂,需要通过修建公路隧道来减轻公路穿越这些复杂地形地貌的修建难度。在修建隧道的过程中会穿越一些特殊地质条件复杂区域,如瓦斯地层、岩溶地层等,容易引发煤与瓦斯突出、突泥涌水等工程安全问题,可能造成严重的工程事故[1-2]。
在隧道建设过程中,原则上应该避免穿越瓦斯煤层等不良地质带,但往往由于多种原因,必须穿越瓦斯煤层时,将会面临煤与瓦斯突出等一系列安全问题。若在隧道揭煤前对于煤与瓦斯突出没有充分的防护准备,不但会发生事故,还会增加施工费用,造成工期延误。
研究隧道揭煤过程中预留岩墙的力学规律变化,对穿越煤层的交通隧道具有一定的安全意义。本文使用相似试验的方法得到2种不同跨度隧道预留岩墙的破坏时的力学性能变化,可为穿越煤层的其他存在煤与瓦斯突出风险的隧道提供岩墙破坏时的力学变化规律以及塑性破坏区的演化规律。
自20世纪50年代以来,学者们纷纷进入实验室,深入研究煤与瓦斯的突出特性,以期揭示其形成的原因。例如: Skochinski[3]首次在实验室中进行了煤与瓦斯的突出试验;Yartsev[4]在实验室中取得了与实际工程中类似的突出结果;Ujihira等[5-8]通过使用煤粉和加气剂制作胶泥状煤体,并进行了试验,结果表明,当煤体暴露在表面时,瓦斯压力会发生显著的变化;Bodziony等[9-11]的试验结果表明,当瓦斯压力超过煤体的抗拉强度时,就会导致煤与瓦斯的突出。
21世纪初,蔡成功[12]为了模拟不同煤层强度、不同应力大小以及瓦斯压力等条件下煤与瓦斯突出的过程设计了三维试验装置,得到应力大小和煤层力学性质决定了突出强度;许江等[13-15]、尹光志等[16-17]、李晓泉等[18]、王维忠等[19]制作了煤与瓦斯突出大型模拟试验装置,可以进行均布荷载和阶梯荷载的加载,对不同倾角的煤层进行煤与瓦斯突出试验,之后在试验装置加装了温度和瓦斯压力传感器等,可以监测煤与瓦斯突出过程中煤层内部温度变化和瓦斯压力变化;王刚等[20]研发了能够综合考量瓦斯压力、地应力和煤层结构的煤与瓦斯突出的模拟试验装置,并进行石门揭煤试验。上述试验对煤与瓦斯的突出进行了控制和重复性试验,力学加载系统的稳定性和可调性有了较大的改进,监测系统的精密性也有了很大提高,为深入认识突出过程提供了有利条件,对瓦斯的发生和发展过程进行了研究,积累了宝贵的经验。但上述研究多是对煤矿施工进行试验,而对于大断面公路隧道的揭煤试验研究还较少,且缺乏考虑不同地质条件对煤与瓦斯突出的影响。
我国隧道规模不断增长,其中穿越煤系地层的瓦斯隧道数量也在增加,但交通隧道的煤与瓦斯突出防治措施与理论相较于煤矿防突措施还不够完善,需要进行进一步的完善研究。本文将基于建立的隧道石门揭煤试验模型,结合相似理论和地质力学模型,在实验室中构建预留岩墙破坏试验平台,进行煤与瓦斯突出隧道预留岩墙破坏力学行为的相似模型试验,研究预留岩墙发生破坏时的力学特性,通过数值模拟研究得到隧道揭煤过程中的预留岩墙安全厚度以及隧道揭煤过程中的预留岩墙集中应力区域以及岩墙厚度,为隧道穿越煤系地层提供施工安全保证和安全监测参考。
1 工程背景
本文依托贵州省正安—习水高速公路天城坝隧道工程,天城坝位于遵义市习水县仙源镇北约5.50 km。根据《贵州省习水县天成煤矿资源储量核实与补充地质勘探报告》,天城坝隧道工程区内含煤地层为二叠系上统龙潭组,有泥岩、砂质泥岩、泥质粉砂岩、细砂岩夹数层薄层灰岩、泥质灰岩、燧石灰岩、煤层及铝质泥岩组成,属海陆过渡带局限海碳酸盐台地潮坪成煤环境。天城坝隧道煤系地层分布如图 1所示。该处地质构造复杂,岩层产状变化较大,岩层倾角一般为27°~42°。煤层数量多,厚度变化大,最厚达到11.2 m;瓦斯质量分数高,C8-2号煤层瓦斯质量分数为21 m3/t;瓦斯压力大,最大达到6.77 MPa。天城坝隧道地质结构复杂、瓦斯质量分数高、煤与瓦斯突出可能性大,在贵州乃至全国都是非常典型的。本文穿越煤系地层隧道施工方法采用中隔壁法(CD 法)开挖施工。为了尽可能地模拟现场的真实情况,模型试验也采用中隔壁法(CD 法)开挖施工进行模型试验隧道的开挖。

C5—C12表示隧道穿越的瓦斯煤层。
2 试验方案设计
2.1 模型试验系统
本试验以贵州天城坝隧道所处地层条件进行试验箱的设计,试验模型的缩尺比例为1∶60。考虑到隧道开挖跨度影响系数、隧道荷载等效高度、边界约束效应,本缩尺模型试验采用2.6 m×2 m×1. 2 m(长×宽×高)的试验箱。试验模型箱示意如图2所示。
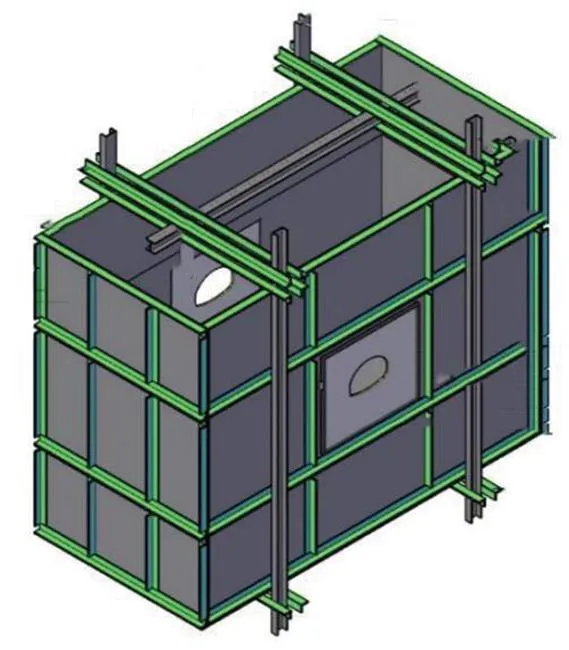
图2 试验模型箱示意图
为了模拟实际工程中瓦斯隧道的高压气体状态,同时保证试验的安全性,本试验使用没有爆炸危险的CO2气体代替瓦斯气体,通过控制CO2钢瓶的输出压力阀来控制CO2喷出的压力,进而模拟隧道瓦斯煤层吸附的瓦斯在开挖后大量释放出的瓦斯气体对前方预留岩墙的作用。其中,钢瓶中的CO2气体压力为5 MPa。充气装置示意如图 3所示。

图3 充气装置示意图
箱体的顶板是一个可以活动的板,在此顶板放上液压千斤顶进行地应力加载。依托工程天城坝隧道在穿越瓦斯煤层工区的隧道埋深取均值400 m,此时模型隧道上方的补充地应力按相似理论计算为0.13 MPa,最终本试验选用的液压千斤顶的液压泵的上限为100 MPa,液压千斤顶能达到的最大力为500 kN,且本试验所设计的反力架能够在15 MPa的压力下不出现明显的形变。
2.2 试验相似比常数的确定
模型试验是否能取得成功,其相似材料参数的合理性是试验的关键因素。本试验对隧道所处原岩相似材料的弹性模量、内摩擦角、泊松比等参数都应与隧道所处真实围岩的对应参数范围满足相似理论关系。通过其相似理论得到各参数的相似常数,其隧道所处岩体的物理力学参数也可以由上述相似比求得。隧道围岩和围岩相似材料物理力学参数如表1所示。

表1 隧道围岩和围岩相似材料物理力学参数
为达到相似模型材料全相似和缩小模型尺度的目的,根据前人的试验和参考文献,岩体相似材料的配置需要骨料作为填充材料,同时加上胶结材料作为黏结剂。结合相关文献和试验经验,确定正交试验各因素水平如表2所示。

表2 正交试验各因素水平
为了对相似材料进行直剪试验从而测定材料的内摩擦角和黏聚力,使用3D打印直径61.8 mm×20 mm的圆柱试件模具。直剪试验每组需3个试件,9组试验需要制备27块试件。
在完成试件制作后对其进行称重并记录其质量,然后根据公式ρ=m/V求得试件密度,在此基础上使用直剪试验仪对其进行抗剪强度的测定。
通过直剪试验可知,调整试验相似材料石膏、土砂比、含水量以及凡士林的含量,使其黏聚力、摩擦角、重度更加靠近模拟岩体参数的值,最终得到直剪试验的配合比下围岩相似材料的性质满足理想围岩相似材料的试验要求,即该配合比的粉砂比为5∶5,石膏质量占比为5%,凡士林质量占比为2%,水质量占比为15%。
2.3 模型体制作及监测点布置
为收集隧道开挖过程中围岩的应力、应变等力学参数,从而得到围岩的力学特性,在试验模型开挖隧道的范围内按照一定的位置埋设多种监测装置,主要有应变片、位移计、土压力盒。
2.3.1 应变采集监测设备
由于本试验测量的是掌子面前方预留岩墙的应变,没法直接在岩墙上贴上应变片,故为了方便试验数据的采集,按照模拟岩体的相似材料配比制作若干个3 cm×3 cm×3 cm的立方体方块,并将应变片用氯丁胶粘贴在立方体表面,用作测量预留岩墙的应变。应变采集点布置如图4所示。用于采集隧道开挖时发生突出前预留岩墙的应变值,从而获得围岩所受的应力。
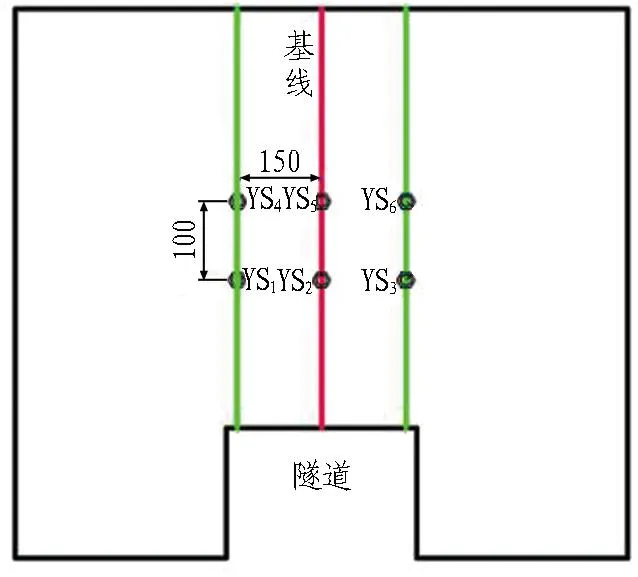
(a) 俯视图

(a) 侧视图
2.3.2 位移监测重采集设备
位移监测点布置如图5所示。在隧道上方每隔200 mm安装3排位移监测点,每排设置2个位移计,位移计应尽量靠近箱体壁面,并且每个位移计之间保持200 mm的距离,主要用于收集隧道开挖过程上部围岩的变形情况。

W1—W6表示隧道上方所在监测平面的位移采集监测点。
2.3.3 压力监测采集设备
在预留岩墙靠近煤层瓦斯充气点的位置设置2组压力的传感器,主要用于监测开挖过程中突出前后预留岩墙压力的演变情况。压力监测传感器布置示意如图 6所示。

(a) 土压力盒纵向布置图
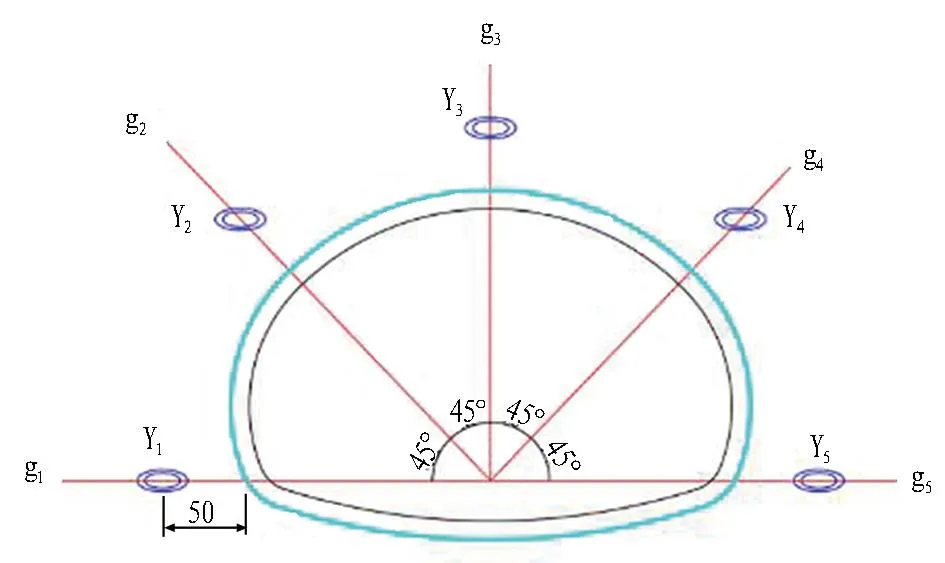
(a) 土压力盒环向布置图
2.4 模拟试验流程
模型试验流程如图 7所示。
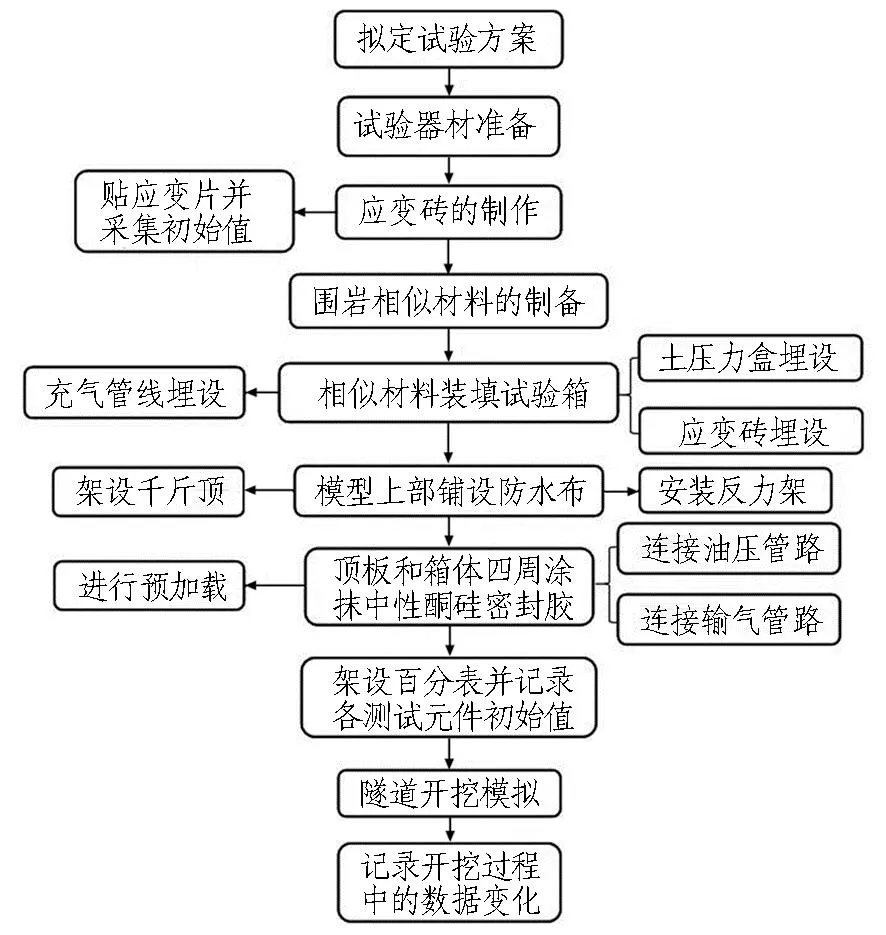
图7 模型试验流程图
3 试验结果
3.1 预留岩墙的应力分析
不同跨度岩墙应力变化情况如图8所示。
由图 8(a)和图 8(b)可以看出: 1)在2种不同跨度的隧道开挖过程中,垂直应力的变化规律都是先增大后减小。其开挖过程中的垂直压力变化规律的原因归于地应力和开挖造成的应力集中会增加围岩的裂隙,降低了岩墙的强度,高压的CO2使岩墙中裂隙充斥着CO2气体,从而使围岩中的垂直压力呈逐步缓慢增加的趋势,随着隧道开挖的进行,围岩岩墙的厚度逐渐变小使CO2气体得到释放,围岩中的垂直应力得到释放,释放的程度取决于开挖的距离。2)当隧道开挖跨度由14.3 cm增加到18 cm后,测点YX1、YX2、YX3达到最大垂直应力的开挖距离由17 cm缩短到15 cm;YX4、YX5、YX6测点达到最大垂直应力的开挖距离由30 cm缩短到25 cm,平均减小了14.15%;且发生应力突变导致岩墙破坏的开挖距离由40 cm缩短到35 cm,说明开挖跨度增大后,隧道掌子面前方预留岩墙的安全厚度增加了12%;各测点最大垂直应力增大了12%。
由图 8(c)和图 8(d)可以看出: 1)当隧道开挖跨度由14.3 cm增加到18 cm后,测点YX1、YX2、YX3的最大水平应力由0.32 MPa增加到0.45 MPa,增大了28.8%;测点YX4、YX5、YX6由0.52 MPa增加到了0.68 MPa,增大了23.5%,说明当跨度增大后预留岩墙的水平应力平均增大了26%。2)在开挖跨度为14.3 cm时,垂直应力最大值是水平应力最大值的1.28倍;开挖跨度增大到18 cm时,垂直应力最大值是水平应力最大值的1.17倍。

(a) 跨度为14.3 cm时的垂直应力变化

(b) 跨度为18 cm时的垂直应力变化

(c) 跨度为14.3 cm时的水平应力变化
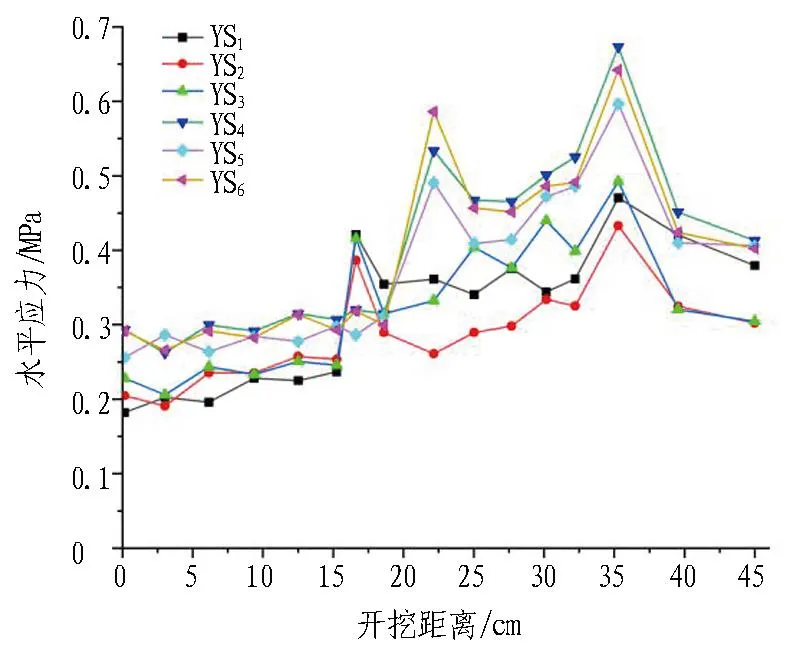
(d) 跨度为18 cm时的水平应力变化
3.2 预留岩墙的四周围岩压力分析
不同跨度预留岩柱四周围岩压力如图 9所示。可以看出: 1)当隧道开挖跨度由14.3 cm增加到18 cm时,拱顶的最大围岩压力由0.35 MPa增加到0.6 MPa,增大了41%;左拱脚的最大围岩压力由0.22 MPa增加到0.35 MPa,增大了37%;左拱腰的最大围岩压力由0.22 MPa增加到0.25 MPa,增大了12%;右拱脚的最大围岩压力由0.25 MPa增加到0.39 MPa,增加了35%;右拱腰的最大围岩压力由0.26 MPa增加到0.39 MPa,增加了33%。说明隧道开挖跨度增大后,预留岩墙四周围岩压力在拱顶和拱脚处增大的较为明显,预留岩墙在拱顶和拱脚处更容易发生破坏。2)开挖跨度越大,隧道围岩的破坏时的岩墙厚度也越大,在施工中大跨度的隧道要预留足够的岩墙厚度,以保证施工的安全。
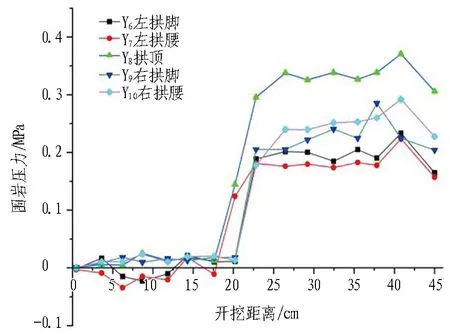
(a) 跨度为14.3 cm时的围岩压力变化
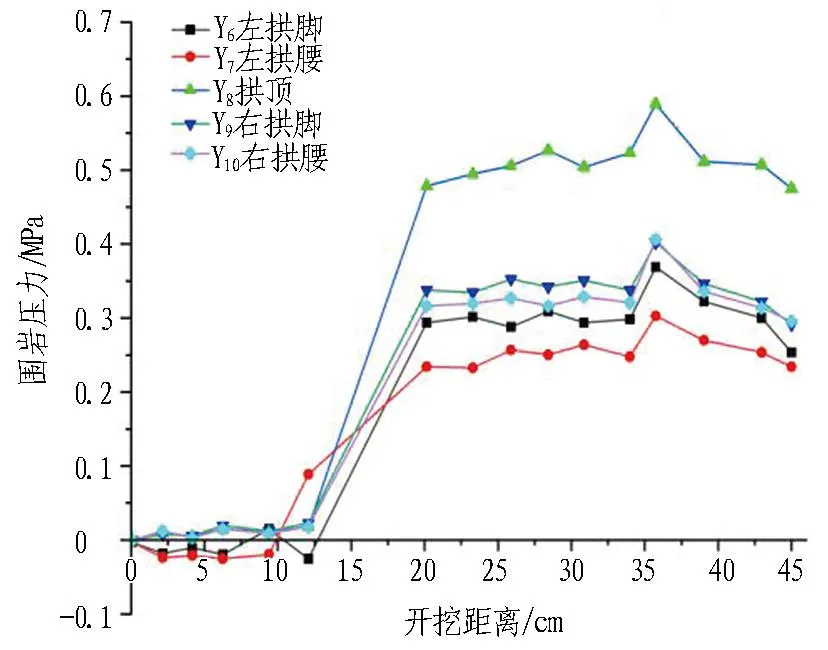
(b) 跨度为18 cm时的围岩压力变化
3.3 预留岩墙的拱顶沉降分析
不同跨度位移变化如图10所示。可以看出: 1)当隧道开挖跨度由14.3 cm增加到18 cm时,W2测点稳定时的位移变化量由11 mm增加到13 mm,增加了15.4%;W5测点稳定的位移变化量由13 mm增加到16 mm,增加了18.7%。位移平均增长了17.1%,说明当隧道开挖跨度增加后,预留岩墙的变形量更大,需要增加预留岩墙的厚度防止其发生破坏。2)随着隧道的开挖,掌子面前方的预留岩墙垂直应力开始增大时,对应的位移监测点的竖向位移开始增大;当掌子面前方的预留岩墙的垂直应力达到最大值时,位移监测点监测到的竖向位移变形也达到最大值;随着隧道继续向前开挖,预留岩墙的垂直应力开始减小,位移监测点监测到的竖向位移变形开始逐渐稳定;最后垂直应力发生突变时,掌子面前方预留岩墙发生破坏,隧道位移监测点的位移量发生突变,快速增大。
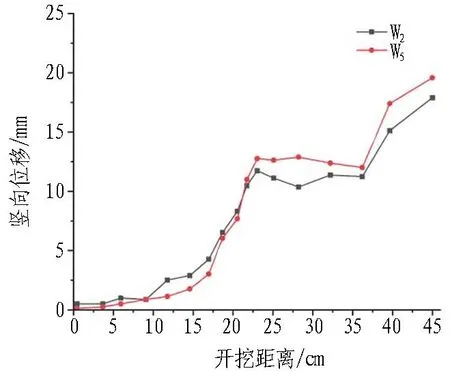
(a) 跨度为14.3 cm时围岩位移变化
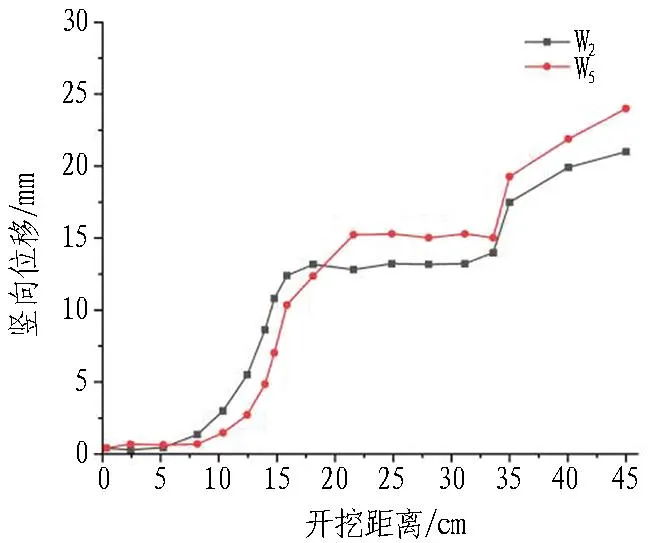
(b) 跨度为18 cm时围岩位移变化
4 气-固耦合作用下岩墙预留厚度的数值模拟
4.1 数值模型的建立
本文利用comsol数值模拟软件,选取天城坝隧道ZK110+295~+445标段作为依托背景,其埋深平均深度为450 m。几何模型设置为50 m(宽)×70 m(高),其隧道开挖跨度为10、11.04、16.03 m,开挖步长为4 m,隧道开挖方式设置为中隔壁法(CD 法)开挖施工。模型四周设置为不透气边界层,上边界为应力补充荷载,将上部的岩石重力转换为均布荷载作用到模型上边界,其荷载大小为5 MPa。模型左右边界为辊支撑,模型中围岩的塑性变形使用Mohr-Coulomb本构模型,将材料简化为均一介质模型且具有各向同性。基于comsol数值模拟软件建立隧道几何模型,网格采用comsol中内置的自动细化网格划分来优化网格划分,同时对隧道开挖位置进行局部的加密处理。几何模型如图 11所示。
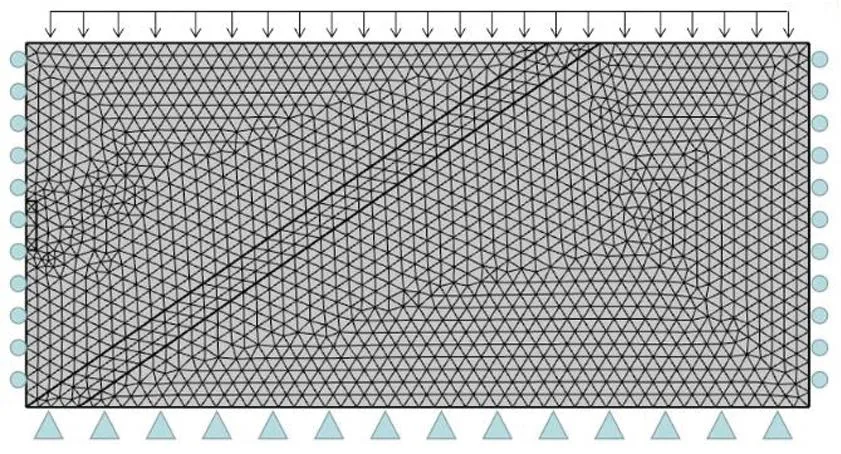
图11 几何模型
4.1.1 模型参数的确定
围岩物理参数如表 3所示。瓦斯气体物理力学参数如表4所示。

表3 围岩物理参数

表4 瓦斯气体物理力学参数
4.1.2 模拟工况的确定
依托工程天城坝隧道煤层的瓦斯压力为2~3 MPa。通过相关文献的研究以及相关规范《公路瓦斯隧道设计与施工技术规范》[21]的查阅可知,当煤层的瓦斯压力大于0.74 MPa时,则认为煤层具有发生瓦斯突出的风险。为了更好地反映不同因素对于瓦斯隧道预留安全岩墙厚度的影响,本文按照围岩等级、瓦斯压力以及隧道开挖跨度进行了不同工况的设置,其中瓦斯压力的变化模数取2.00 MPa,将其划分为 0.74、2.00、4.00 MPa。
为了考虑不同跨度对隧道预留岩墙厚度的影响,根据规范《公路隧道设计细则》对公路隧道建筑限界横断面组成最小宽度以及支护和预留变形量的要求,分别选取三级公路(40 km/h) 2车道、一级公路(100 km/h) 2车道、一级公路(120 km/h) 3车道3个不同跨度进行研究。三级公路2车道跨度为10.00 m、高度为7.85 m;一级公路2车道,跨度为11.40 m、高度为8.7 m;一级公路3车道,跨度为16.03 m、高度9.8 m。由于本文数值模拟为二维结构模型,数值模拟中取的是不同跨度隧道的断面高度进行数值计算。不同工况的参数设置如表 5所示。

表5 不同工况的参数设置
本次数值模拟中选择3个影响隧道开挖掌子面前方与瓦斯煤层间预留岩墙厚度的因素,并且根据正交试验的原理设置模拟工况,用以分析3个不同因素对预留岩墙稳定性和厚度的影响。正交工况的设置如表6 所示。

表6 正交工况的设置
4.2 模型计算结果分析
4.2.1 预留岩墙最小厚度分析
确定隧道掌子面与煤系地层间预留岩墙的最小安全距离,需要判断隧道预留岩墙的稳定性。其稳定性判定依据主要有应力等值线、围岩的塑性形变和位移以及围岩的破坏区等因素。对9种工况下的隧道进行数值模拟,得到9种工况下瓦斯煤层与掌子面之间预留岩墙的最小厚度计算结果。不同工况下最小安全岩墙如表 7所示。

表7 不同工况下最小安全岩墙
通过对影响大断面隧道预留岩墙最小厚度的不同因素进行极差分析,得到不同影响因素的极差R值。通过分析不同影响因素的极差R值与预留岩墙厚度之间的关系,来判断其对岩墙最小厚度的影响程度。若R越大,则该因素对岩墙厚度的影响越大,也越重要,可以通过极差R值的大小进行主次因素的判断。预留岩墙最小厚度影响因素极差分析如表8所示。

表8 预留岩墙最小厚度影响因素极差分析
若对应影响因素的极差较大,说明该因素对预留岩墙厚度的变化影响较大。由表 8可知: 安全岩墙厚度影响因素排序为瓦斯压力、隧道跨度、围岩等级,且瓦斯压力和隧道跨度对预留岩墙厚度的影响相差不大。根据表8绘制出不同影响因素和岩墙最小厚度之间的关系变化趋势,如图 12所示。
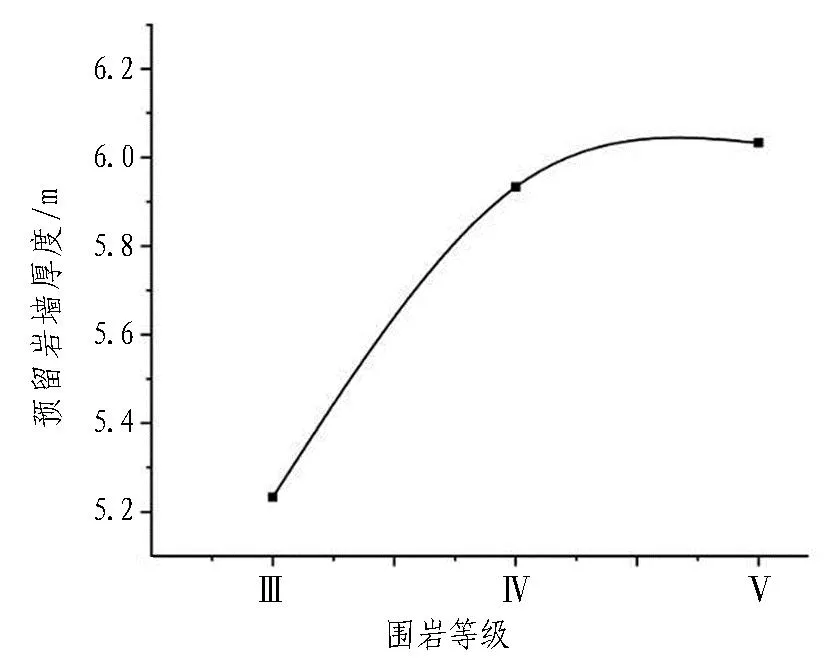
(a) 围岩等级
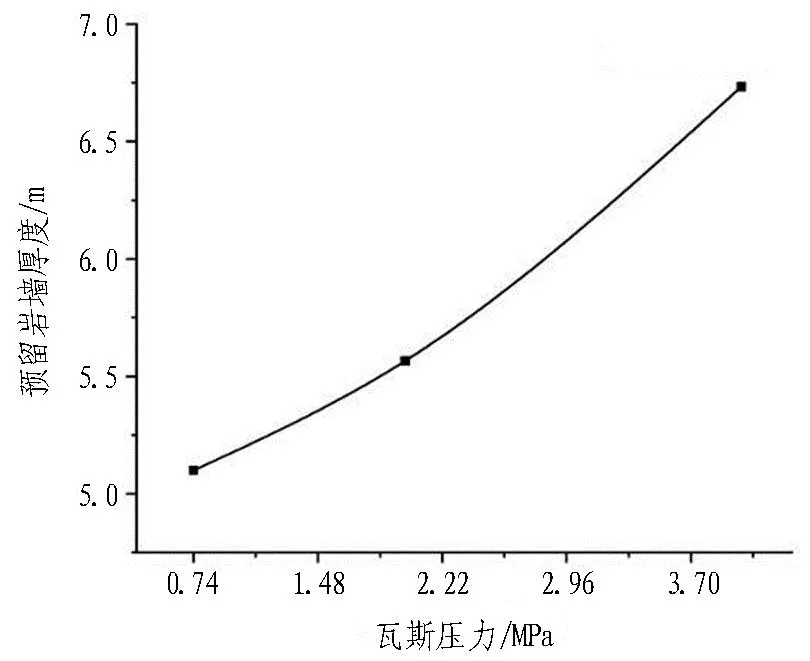
(b) 瓦斯压力
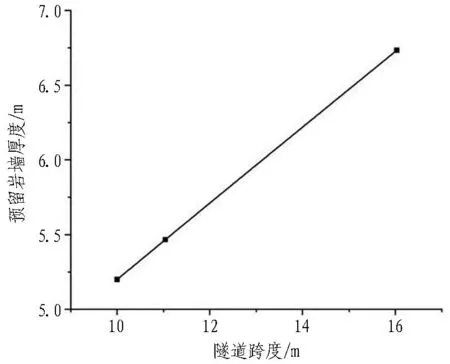
(c) 隧道开挖跨度
1)由图12(a)可以看出: 当围岩等级从Ⅲ级变到Ⅳ级和Ⅳ级变到Ⅴ级的增长率不相同,其Ⅳ级变到Ⅴ级的增长率显著下降。对于Ⅳ级和Ⅴ级围岩来说,围岩的等级对预留岩墙厚度的影响变化不显著。
2)由图12(b)可以看出: 针对隧道瓦斯压力,掌子面前方的预留岩墙厚度与瓦斯压力的关系大致成二次函数关系,即当瓦斯压力增大时,预留岩墙的厚度增大。煤层瓦斯压力越大,对前方预留岩墙的塑性破坏影响越大,瓦斯压力的增大会使预留岩墙的破坏区更容易贯穿煤系地层,导致隧道掌子面前方的预留岩墙发生破坏,为煤与瓦斯突出提供条件,因此预留岩墙的厚度随着瓦斯压力的增加呈线性变化,即瓦斯压力越大预留岩墙越厚。
3)由图12(c)可以看出: 掌子面前方预留岩墙厚度随隧道跨度的增大而增大。因为隧道开挖断面越大致使隧道的临空面越大,从而应力的变化越大,围岩的塑性破坏区也越大,且当隧道开挖跨度从10.00 m变化到11.04 m时预留岩墙的厚度增长率为4.88%;当隧道开挖跨度从11.04 m变化到16.03 m时预留岩墙的厚度增长率为18.81%。隧道开挖跨度的逐渐增大预留岩墙厚度的变化率也越大,开挖跨度对预留岩墙的厚度影响也越大。
4.2.2 预留岩墙厚度分析
根据上述极差分析结果,对预留岩墙的厚度和不同因素之间建立多元回归模型进行分析。通过决定系数R2来反映模型拟合数据的准确程度。一般来说,R2为0~1,若其数值离1越近,说明该回归模型对数据的拟合程度越好;其值越接近0,表明模型拟合的越差。一般来说R2>0.4,拟合效果较好。
4.2.2.1 隧道围岩等级和预留岩墙厚度的一元回归模型
围岩等级和岩墙厚度回归模型如图13所示。
二次拟合:y=-0.304 5x2+2.833x-0.535 5。
三次拟合:y=-0.021 7x3-0.047 29x2+1.83x-
0.750 8。
二次拟合相关系数:R2=0.999 1。
三次拟合相关系数:R2=0.999 2。
由图 13可知: 1)隧道围岩等级和预留岩墙厚度的回归拟合模型中二次拟合和三次拟合的R2均大于0.4,即2种拟合程度均较好。2)其残差图中二次拟合和三次拟合的RMSE分别为0.046 856和0.042 964,且二者的残差均是随机分布在0线附近,即二者的残差都落在0线这条变化幅度不大的直线之内,说明了2种拟合模型效果均很好。

(a) 围岩等级和预留岩墙厚度的拟合图
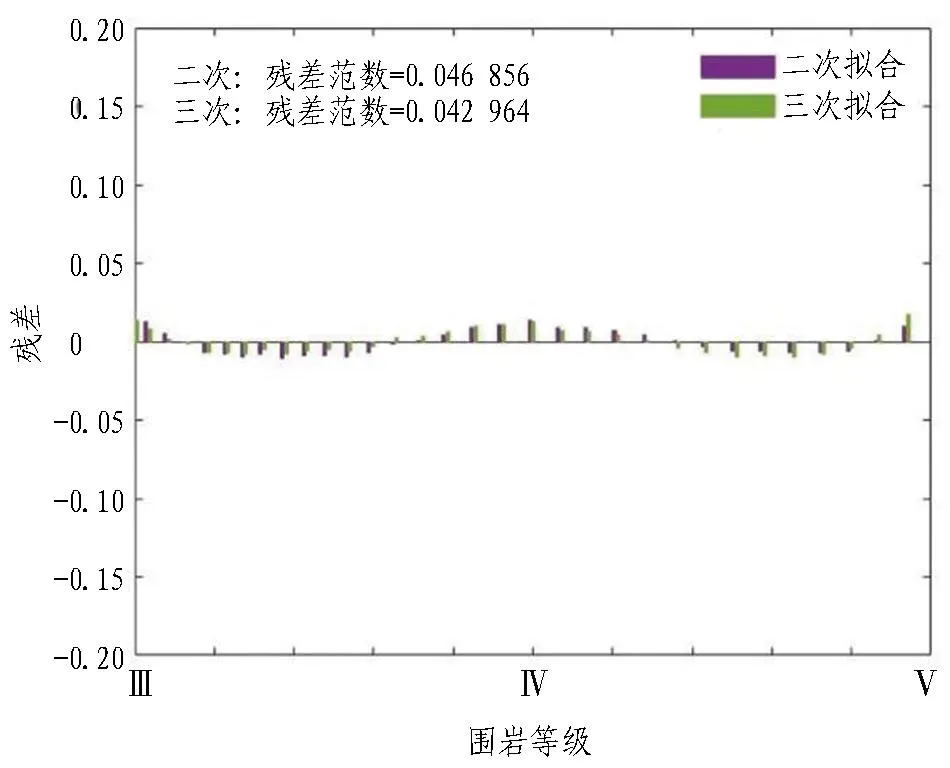
(b) 围岩等级与岩墙厚度残差图
4.2.2.2 煤层瓦斯压力与预留岩墙厚度的一元回归模型
瓦斯压力和岩墙厚度回归模型如图14所示。
线性拟合:y=0.513 7x+4.618。
二次拟合:y=0.068 63x2+0.196x+4.924。
线性拟合相关系数:R2=0.987 4。
二次拟合相关系数:R2=0.999 8。
由图 14可知: 1)瓦斯压力和预留岩墙厚度的回归拟合模型中线性拟合和二次拟合的R2分别为0.987 4和0.999 8,数值均大于0.4,即2种拟合程度均较好。2)其残差图中线性拟合和二次拟合的RMSE分别为0.300 99和0.035 464,此时线性拟合的残差为抛物线形,没有均匀地分布在0线附近,说明线性拟合欠佳,模型结构不正确,模型中应该包含二次项。而对于二次拟合,其残差图中残差都落在0线这条变化幅度不大的直线之内,说明了二次拟合模型效果好于线性拟合的模型效果。

(a) 瓦斯压力和预留岩墙厚度的拟合图
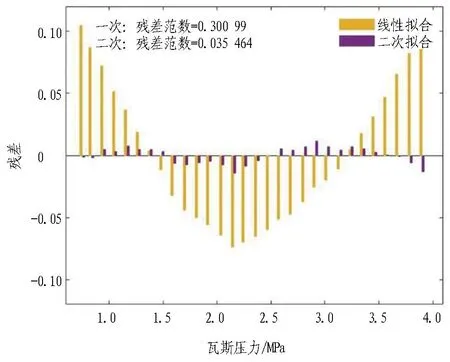
(b) 瓦斯压力与岩墙厚度残差图
4.2.2.3 隧道开挖跨度与预留岩墙厚度的一元回归模型
隧道跨度和岩墙厚度回归模型如图15所示。
线性拟合:y=0.255x+2.66。
线性拟合相关系数:R2=0.999 9。
由图 15可知: 1)隧道开挖跨度和预留岩墙厚度的回归拟合模型中线性拟合R2为0.999 9,数值均大于0.4,即线性拟合程度较好。2)其残差图中线性拟合的RMSE分别为0.018 3,残差均是随机分布在0线附近,线性拟合的残差在0线附近分布较为集中,且是均匀分布在0线附近,故线性拟合模型效果不错。
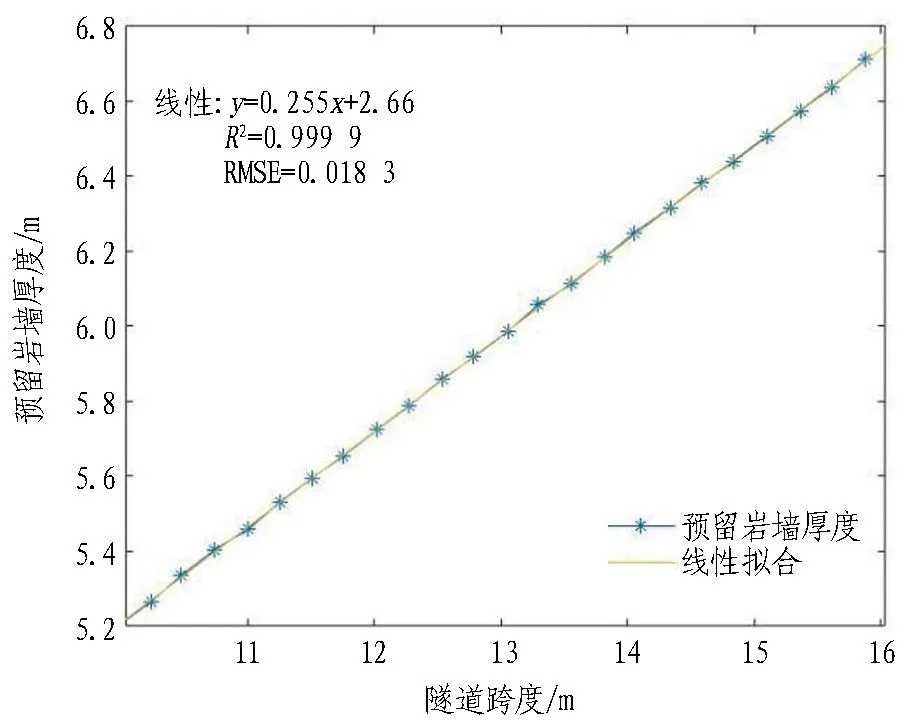
(a) 隧道跨度和预留岩墙厚度的拟合图

(b) 隧道跨度与岩墙厚度残差图
通过上述一元回归分析,对影响预留岩墙厚度的因素建立多元回归模型,基于以上分析将安全岩墙厚度结果导入 SPSS 软件中,构建多元回归模型

式中:y为预留岩墙的厚度;x1为隧道围岩等级;x2为瓦斯压力水平;x3为隧道开挖跨度。
在本数值计算中的岩体模型是理想化后的均一介质模型,这与实际工程中的实际岩体情况有着一定的区别,因此对于多因素条件下的预留岩墙厚度的回归拟合需要设定安全系数N,用以提高其安全性。通过文献查阅,安全系数的取值一般为1.2~1.5[21-22],可得到预留岩墙厚度经验计算公式:

对上述预留岩墙厚度回归式进行显著性检验,结果如表9和表10所示。

表9 预留岩墙厚度方差分析
由表9可知: 对多元回归方程进行显著性概率检验,P=0.045<0.05,则说明多元回归模型中预留岩墙的厚度和瓦斯压力、围岩等级、隧道开挖跨度等自变量之间存在线性相关,且多元回归方程相关性显著。

表10 回归系数表
由表10可知: 对于围岩等级(b=0.400,β=0.382,P=0.032)、瓦斯压力(b=0.085,β=0.134,P=0.035)、隧道跨度(b=0.240,β=0.740,P=0.021)均会影响预留岩墙的厚度,且围岩等级、瓦斯压力、隧道跨度均为正向预测(因为回归系数b均为正)预留岩墙厚度,且显著性概率P小于0.05,认为变量显著。
共线性统计包括方差膨胀因子(VIF)和容差2个指标,事实上,VIF=容差的倒数(1/容差),只需要判断其中1个指标即可。如果容差小于0.1(或方差膨胀因子大于10),提示数据存在多重共线性。在本研究中,所有容忍度值都大于0.1(最小值为0.9),说明本研究自变量多重共线不严重,影响因素和预留岩墙的厚度之间有较好的线性关系。
5 结论与建议
1)以遵义市天城坝隧道隧址区的F4断裂层瓦斯煤层为工程背景,通过三维模型试验模拟在不同跨度隧道开挖过程中遭遇瓦斯煤层和断裂层时随预留岩墙的厚度变化的全过程。隧道开挖改变了围岩的原始应力状态,在隧道掌子面前方的岩墙出现应力集中,且隧道在开挖后掌子面一侧的应力卸载使竖向应力和水平应力差值最大。同时通过摩尔-库仑理论,岩墙容易发生破坏的区域为掌子面和其前方一定范围内的岩墙,越远离掌子面破坏越小。
2)使用突变理论分析了岩墙的稳定性,得出当隧道所在的地质环境相同时,预留岩墙上部垂直地应力越大,隧道的开挖跨度越大,预留岩墙的厚度及弹性模量越小,预留岩墙发生破坏失稳的可能性越大。
3)随着隧道的开挖,掌子面前方的预留岩墙垂直应力开始增大时,对应的位移监测点的竖向位移开始增大;当掌子面前方的预留岩墙的垂直应力达到最大值时,位移监测点监测到的竖向位移变形也达到最大值;随着隧道继续向前开挖,预留岩墙的垂直应力开始减小,位移监测点监测到的竖向位移变形开始逐渐稳定;最后垂直应力发生突变时,掌子面前方预留岩墙发生破坏,隧道位移监测点的位移量发生突变,快速增大。
4)通过数值模拟得到了在不同瓦斯压力、围岩等级等不同因素下的预留岩墙厚度的变化规律,通过多因素回归算法拟合得到了岩墙厚度的最小经验公式。
5)根据天城坝隧道的实际工况进行计算可知,天城坝隧道在开挖过程中揭煤的最小预留岩墙厚度理论上应为5.9 m,在《公路瓦斯隧道设计与施工技术规范》[21]对防突措施要求检验的最小厚度为5 m,故对于隧道如果依据规范在5 m处进行瓦斯突出安全检验,发生煤与瓦斯突出的风险较高,因此需要增加预留安全岩墙检验厚度,从而降低煤与瓦斯突出的可能性。
