富水砂卵石地层盆形冻结止水技术研究
2024-02-21张晋勋江玉生宋永威杨志勇
张晋勋, 江玉生, 杨 昊, 亓 轶, 宋永威, 江 华, 杨志勇
(1. 北京城建集团有限责任公司, 北京 100088; 2. 中国矿业大学(北京)力学与土木工程学院, 北京 100083)
0 引言
随着经济的快速发展,我国工程建设特别是地下工程建设速度居于世界前列。与此同时,由于地质条件的复杂性,地下工程与地下空间的安全建设与风险管理也成为突出问题[1]。富水砂卵石地层是地下工程施工中的常见地层,该类地层结构松散、自稳能力弱、颗粒间的空隙大、黏聚力小,是典型的力学不稳定地层,并且在地下水渗流作用下物理力学性质越发复杂。
近年来,国家不断加强对地下水资源的保护力度,北京地区作为水资源改革试点城市,开展在地下工程领域施工过程不降水(或少降水)的研究工作变得十分重要。冻结法最早被应用在采矿工程领域,因其灵活可控、绿色环保的特点被引入市政工程中[2-6]。随着地下工程开挖深度的增加、工程建设规模的扩大,冻结法应用边界不断被拓展。朱泽萱等[7]将冻结法应用于福州地铁2号线紫阳站—五里亭站区间的66 m超长联络通道工程,通过精确控制冻结孔的成孔精度和角度保证冻结效果。王磊等[8]基于上海轨道交通18号线江浦路车站管幕冻结暗挖工程,通过模型试验的方法研究了管幕+冻土复合结构在大体量冻结工程中应用时的冻胀特性。胡指南等[9]提出了软土地层双线盾构区间隧道扩建地铁车站的插管冻结法,对冻结法扩建地铁车站施工过程中的结构变形、受力及地表沉降特性等进行分析。杜宝义等[10]以厦门地铁过海区间隧道工程为例,分析了海底隧道盾构开舱辅助工法,研究发现在海底砂质土地层中,冻结法加固效果良好,满足盾构常压开舱需求。同时,基于冻结工程在北京地区的应用前景,北京市出台了地方标准《城市轨道交通工程冻结法施工技术规范》[11]。
上述工程或针对冻结进行单一方向的局部控制,或针对软土地区进行冻结施工,或采用其他相关技术辅助冻结效果,而对富水砂卵石地层,特别对于地下水渗流影响无法被忽略的工程条件,上述研究或不再适用。
为解决全断面砂卵石地层地下工程地下水控制治理难题,张晋勋等[12-15]提出了盆形冻结止水技术。这是该冻结技术在市政工程领域的全新应用,冻结断面将达到万m2级,极大地突破了冻结的规模。本文总体论述冻结砂卵石力学特性及盆形冻结施工控制技术。根据实际工程的需求,通过大量的室内试验,详细分析砂卵石冻结体的强度、变形、冻胀融沉特性;为验证盆形冻结的止水效果,通过大型物理模型试验和数值模拟的方法,分析渗流条件下盆形冻结温度场及冻结形态的演化过程。同时为了提高效率、节约资源,依据盆形底部表现出的“群孔效应”,提出积极冻结期合理间距的确定与布置技术,并针对盆形冻结的维护冻结期,提出切割局部冻结管的方法以对冻结区域进行精细化控制。
1 盆形冻结止水技术简介
盆形冻结止水技术可用于深度较大,且地下无有效隔水层的大体量工程。盆形冻结结构由盆壁和盆底2部分组成,如图 1 所示。

(a) 剖面图

(b) 平面图
盆壁环拟建在地下工程四周,采用通长冻结管布置,冻结管所形成的冻土柱最终交圈连接成为环形冻结帷幕;盆底则在拟建范围内规则布置竖向矩阵式冻结管,盆底冻结管上部包裹保温材料,采用局部冻结的方式形成水平冻结板。冻结帷幕和水平冻结板共同作用,阻断外部水力联系,形成隔水空间,二者包围的区域即为地下工程开挖工作空间。
2 砂卵石冻结体的力学特性
富水砂卵石地层是地下工程施工中常见的不稳定地层,其复杂的力学性质常常制约了工程的进度。冻结条件下的富水砂卵石地层力学特性更为复杂。为真实反映冻结条件下砂卵石地层的特性,进行不同温度、围压下的三轴强度及蠕变试验,以获得冻结砂卵石的力学参数。三轴及蠕变试验试样均采用尺寸为φ50 mm×100 mm的冻结圆柱体,并采用等效替代法[16]将试样中的超粒径部分用2~10 mm的粗粒土按质量百分比替代,替代后的颗粒级配曲线如图2所示。等效替代后最大粒径为10 mm,并多次振捣,达到原状土密度。将试样饱水处理48 h后,转入数控冻结试验箱(误差±1 ℃)内恒温-15 ℃处理7 d,随后拆模并调节冻结试验箱温度至-10 ℃,再将试样放置其中(至少24 h)备用。
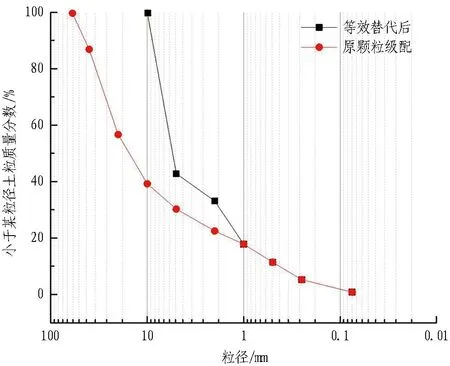
图2 砂卵石颗粒级配
2.1 冻结砂卵石三轴压缩力学特性
根据以往经验,确定试验温度为-5、-10、-15、-20 ℃,围压为 0、0.3、0.8、1.3、2、3、4、8 MPa,三轴试验结果见表1及图3。

表1 不同温度和围压条件下砂卵石力学参数
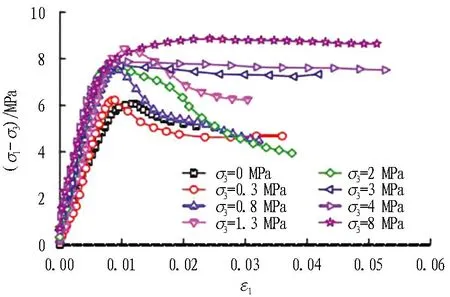
(a) -5 ℃
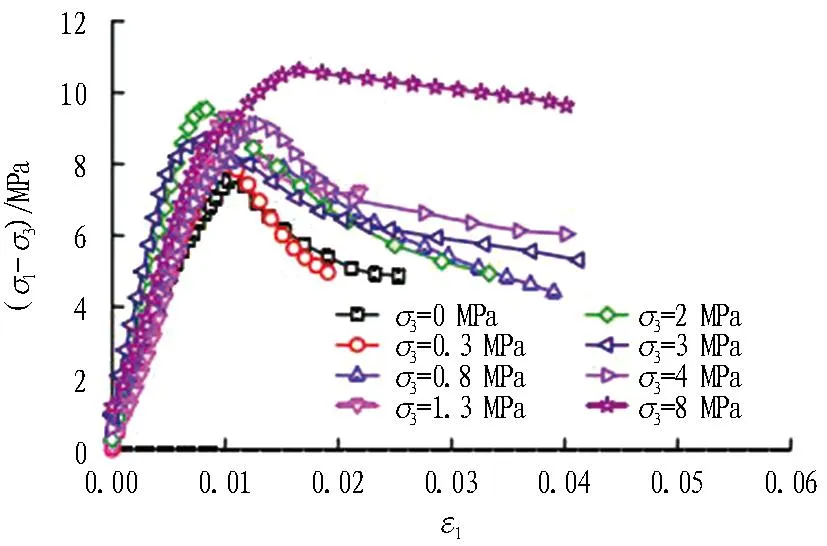
(b) -10 ℃
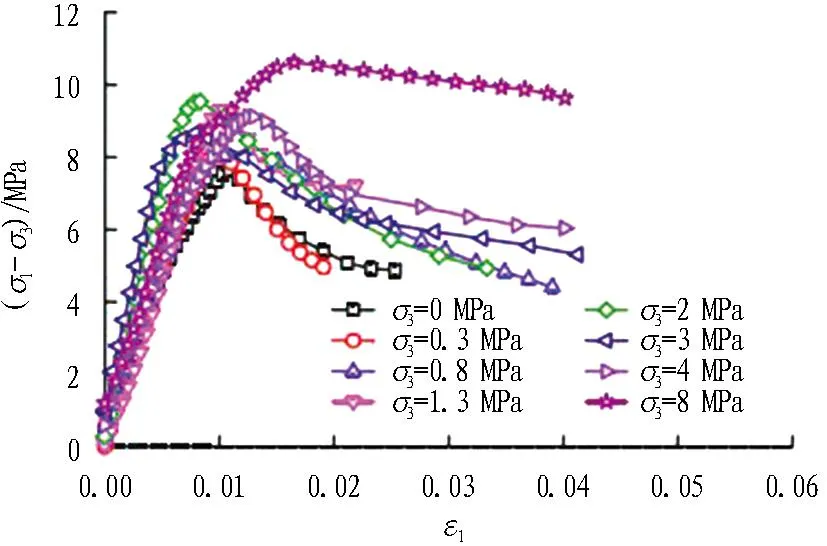
(c) -15 ℃

(d) -20 ℃
图3中,σ1为轴向压力;σ3为围岩压力;ε1为应变。由表1可知: 冻结砂卵石弹性模量在低围压条件下变化不规律,随着围压增大,逐渐呈规律性增大趋势,这一变化符合多孔隙材料弹性模量随围压增加而增大的结论。由图3及表1可知: 当温度较高,围压<3 MPa时,冻结砂卵石破坏形式以应变软化为主;当温度较低,围压较大(≥3 MPa)时,以塑性破坏为主。这主要是因为砂卵石含水率较高,冰的变形性质起主导作用。低围压(<3 MPa)条件下,三轴抗压强度与围压呈正线性相关,围压继续增大时,由于砂卵石变成承载骨架,冰的作用弱化,其承载力基本不变[17]。
2.2 冻结砂卵石三轴蠕变力学特性
为分析冻结砂卵石蠕变特性,基于损伤理论建立适用于冻结砂卵石不同蠕变特征的计算模型,如图4所示[18]。
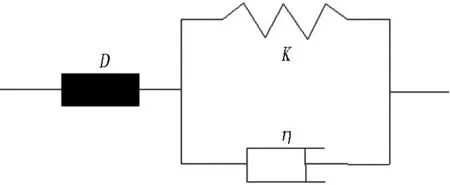
图4 蠕变损伤模型
该模型由2部分组成: 右侧为开尔文体(弹性体K+黏壶体黏滞系数η),左侧为损伤体D。总应变ε等于损伤体应变εD与开尔文体的应变εkη之和,即
ε=εD+εkη。
(1)
图4中右侧开尔文体应变理论公式可表示为
(2)
式中:σ为应力差,等于σ1-σ3,MPa;E为弹性体的弹性模量,MPa;t为蠕变时间。
对于损伤体D,其受力符合:
σD=σkη=σ。
(3)
σD=EDεD(1-D)。
(4)
式中:σD为损伤体受到的力;σkη为开尔文体受力;ED为损伤体弹性模量。
根据文献[19]的相关成果,假设冻结砂卵石的dD/dt为:
(5)
式中a、b为相关参数。
对式(5)进行积分可得
(6)
式中tc为蠕变总时长。
冻结砂卵石在荷载相对较小时表现为衰减型蠕变,此状态下,冰起主导作用,在低温条件的冰迅速重组,损伤很小;当σ≥σc(σc为长期强度,MPa)时,损伤产生并逐渐增大至试样破坏,即
(7)
式中令1/(1+b)=α。
结合式(1)和式(7)可得其全过程蠕变模型为:
(8)
由式(8)可以发现:σ≥σc时,冻结砂卵石的ε与σ呈正比,无限增大;σ<σc时,其ε符合开尔文体变化模型。根据式(8)对多组试验数据拟合,拟合参数见表2,实测结果与拟合结果对比见图5。
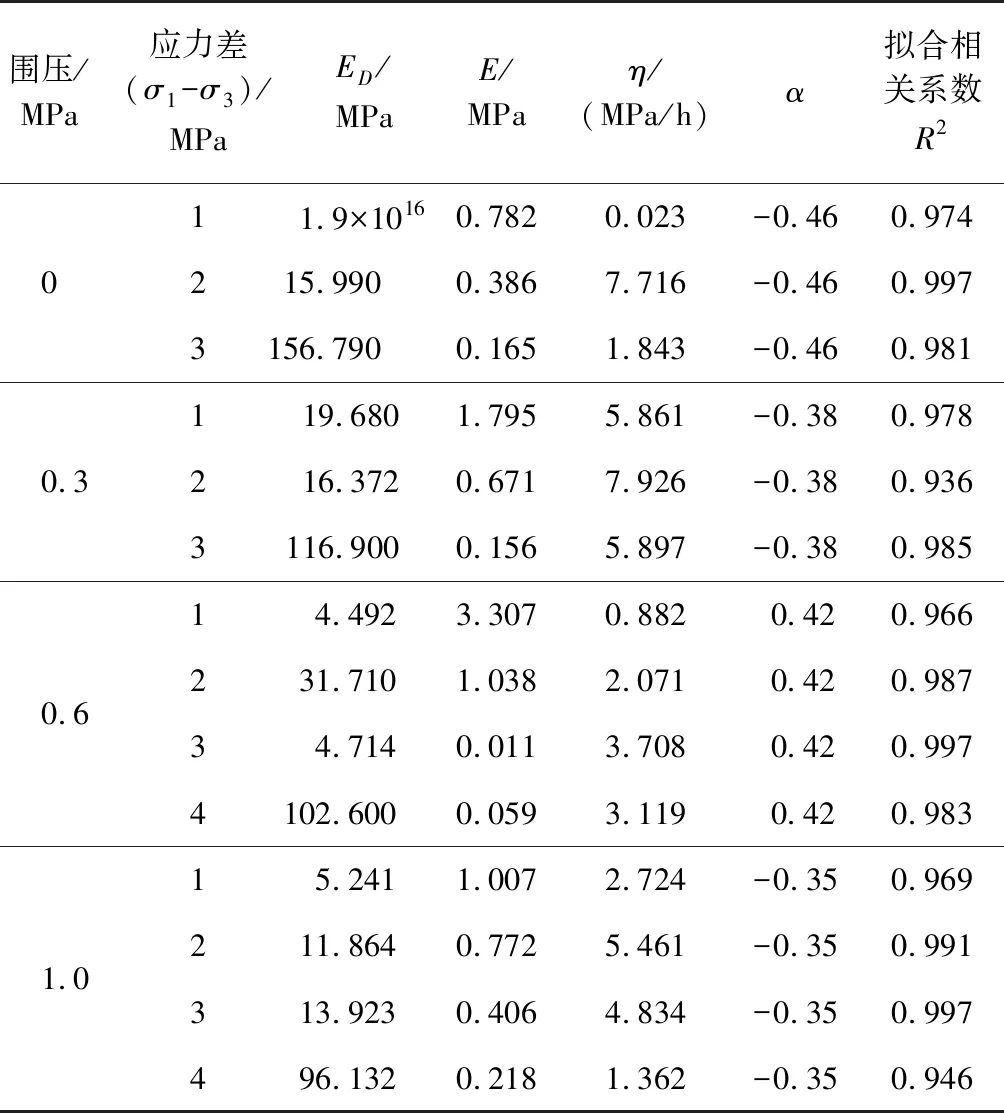
表2 拟合参数
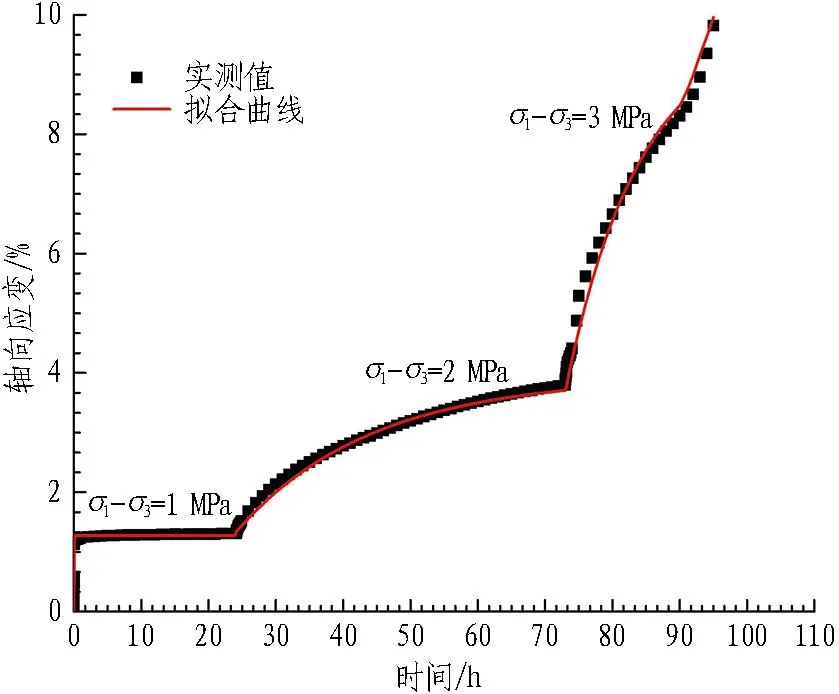
(a) 围压0 MPa
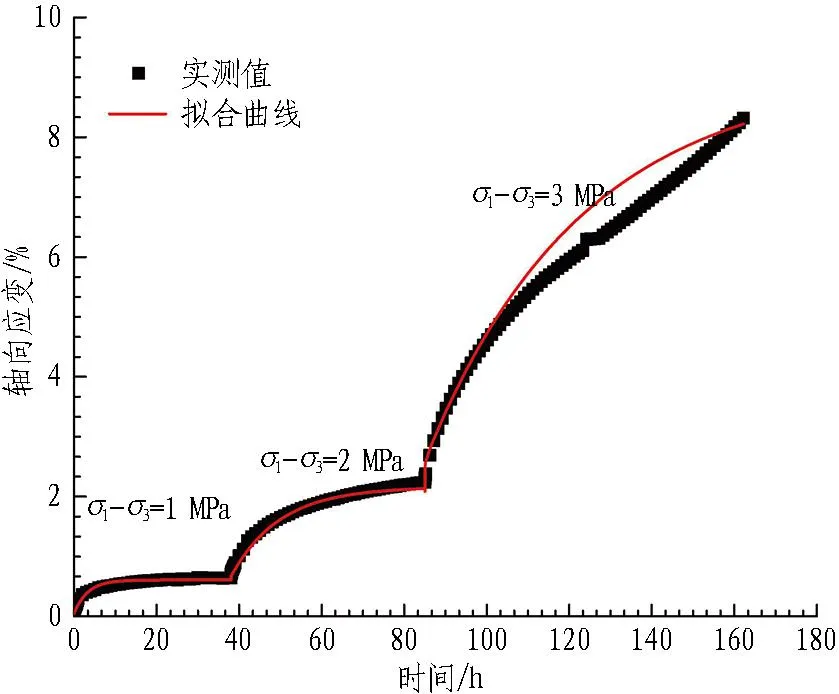
(b) 围压0.3 MPa
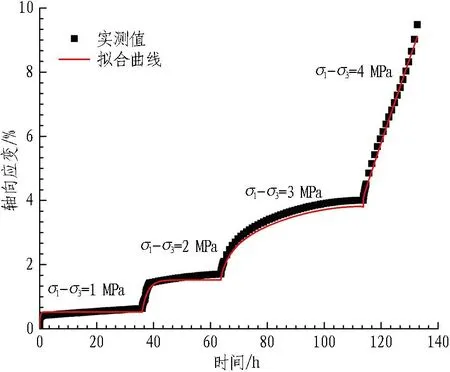
(c) 围压0.6 MPa
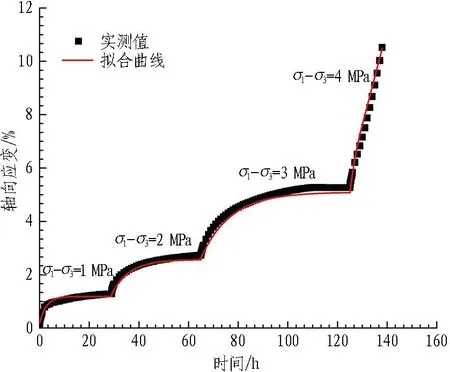
(d) 围压1 MPa
由表2可知,新建模型拟合相关系数均在0.936以上,试验数据标定的模型参数较好。实际工程设计施工中,冻结壁设计温度一般为-10 ℃,该模型可为冻结设计提供参考。
2.3 砂卵石冻胀融沉特性
为更加准确得到砂卵石的颗粒级配,方便冻胀融沉试样配比,重复5次筛分试验,将求得的平均值作为原状土砂卵石颗粒级配。原状砂卵石级配曲线如图6所示。根据原状土含水率、密度、细粒土质量分数及荷载制备试样,试样高度H=150 mm,直径D=300 mm,在团队自主研发的多功能冻胀融沉仪中进行,如图7所示。试验装置主要由高低温制冷机、有机玻璃筒、下冷浴盘、温度传感器、电子位移传感器、流量计及数据采集终端等组成[20]。荷载采用标准铁块堆载,单个铁块质量为24.75 kg。每2块铁块为1组荷载试验,每做完1组试验再重新制备试样进行下组试验。
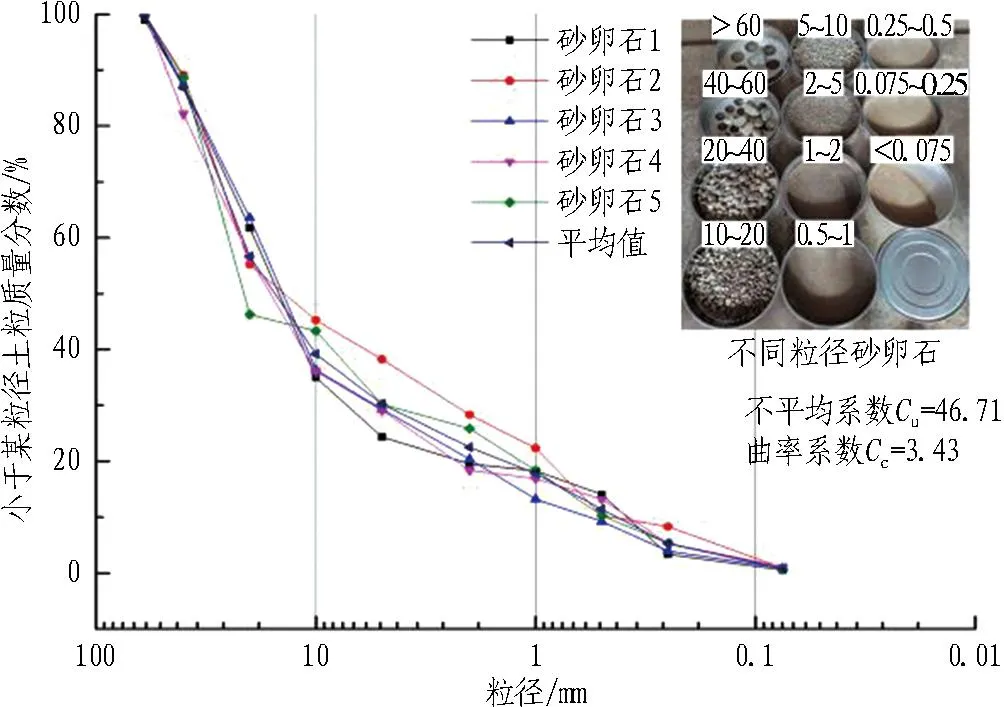
图6 原状砂卵石级配曲线

(a)

(b)
对细粒土(原砂卵石筛分出的粒径小于0.075 mm的土)质量分数为0.82%、3%、6%、10%及20%的饱和砂卵石进行0、7、14、21 kPa有载冻胀融沉试验(开敞系统),冻胀融沉系数与荷载及细粒土质量分数关系曲线见图8。

(a) 荷载与冻胀率关系
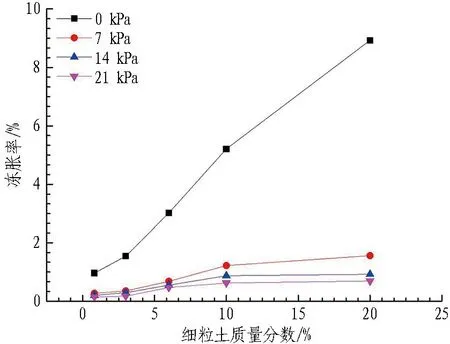
(b) 细粒土质量分数与冻胀率关系
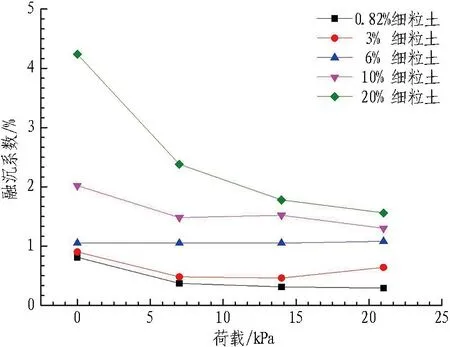
(c) 荷载与融沉系数关系
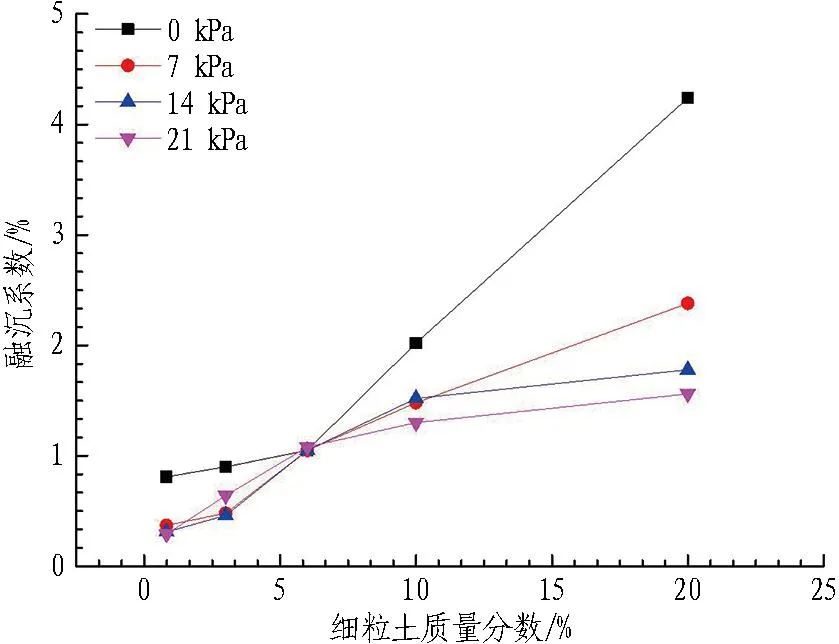
(d) 细粒土质量分数与融沉系数关系
由图8可知,冻胀率具有明显的荷载敏感性,当细粒土质量分数小于10%时,荷载对融沉系数影响较小。随着荷载的逐渐增大,不同细粒土质量分数的砂卵石试样冻胀率降低幅度均越来越小,冻胀率逐渐趋于平缓。相同荷载条件下,饱和砂卵石融沉系数随着细粒土质量分数的增加而增大。
为更好地研究荷载及细粒土质量分数对饱和砂卵石冻胀融沉特征的影响规律,假设符合函数:
η冻=a1+b1w细+c1exp(d1σ)。
(9)
α融=a2+b2w细+c2exp(d2σ)。
(10)
式中:a1、a2、b1、b2、c1、c2、d1、d2均为与砂卵石土质参数有关的试验常数;w细为细粒土的质量分数;η冻为冻胀率;α融为融沉系数。
采用origin对20组试验数据进行拟合,可得:
η冻=0.159+3.305w细+4.822exp(-0.232σ),R2=0.836。
(11)
α融=0.087+1.109w细+3.861exp(-0.171σ),R2=0.874。
(12)
由拟合结果可以发现,拟合相关系数分别为0.836及0.874,说明拟合结果良好。依据拟合函数进行插值法可得不同细粒土质量分数、荷载下的饱和砂卵石冻胀融沉三维预测图,如图9所示。

(a) 冻胀率三维预测图
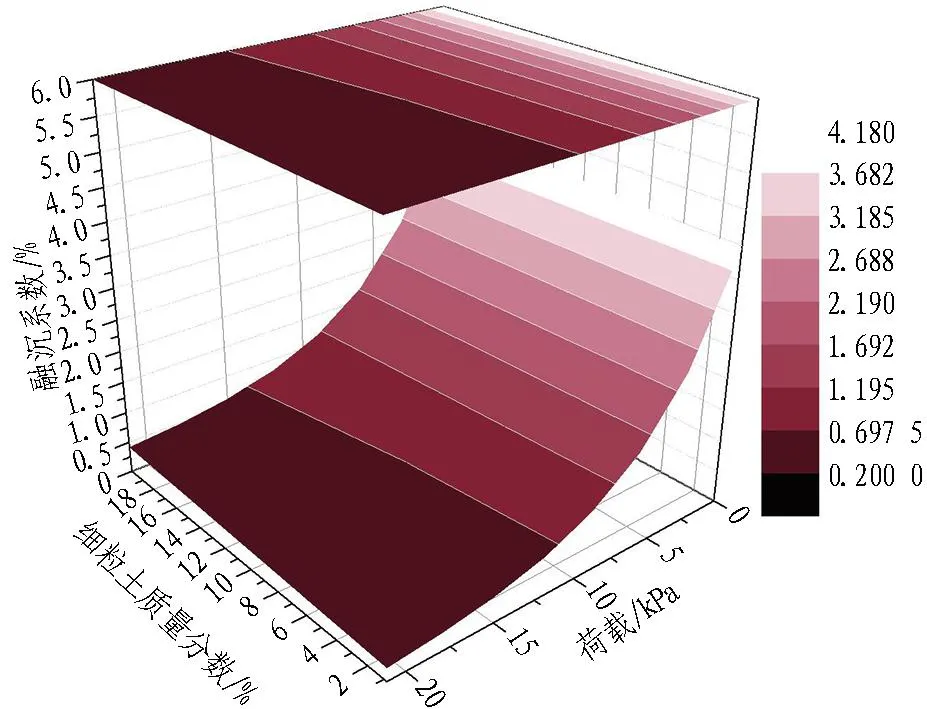
(b) 融沉系数三维预测图
3 盆形冻结的温度场扩展规律
冻结砂卵石的力学及冻胀融沉特性分析说明,具有一定体积的冻结砂卵石可以抵御周围的水土压力。本文所提出的盆形冻结,旨在阻断待开挖区域外部水力联系,其冻结体量巨大,故研究盆形冻结温度场扩展规律对冻结结构的有效成型至关重要。
本节采用大尺度冻结模型及有限元分析相结合的方法,分析地下水流速对温度场发展、冻结形态的影响。模型试验针对所研究的问题,在主要条件上满足相似关系,遵循最大限度突出模拟核心元素并消除边界效应的原则。本次研究所选择的几何相似比为Cl=1∶10。根据相似准则的π定理,分析过程中所涉及的参数相似比见表3。

表3 模型试验参数相似比
表3中,l为包括冻结管尺寸、冻结管间距在内的几何尺寸; T为温度; t为时间; v为流速; 下标m为模型,p指原型。物理模型试验采用自主研发的渗流冻结模型试验平台进行操作,试验模型长×宽×高=10m×3m×2.5m。冻结管布置方案如图10所示。
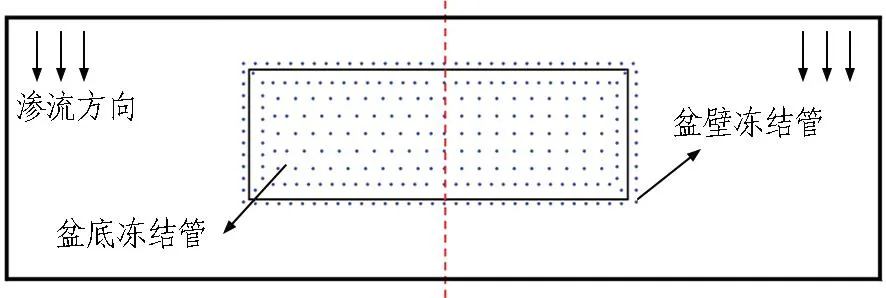
图10 冻结管布置方案
物理模型、数值模拟参数及边界条件如表4所示,在后续分析中仅对右侧对称部分进行分析。封顶前的物理模型试验箱见图11,从中可以看到冻结管的排布形式。
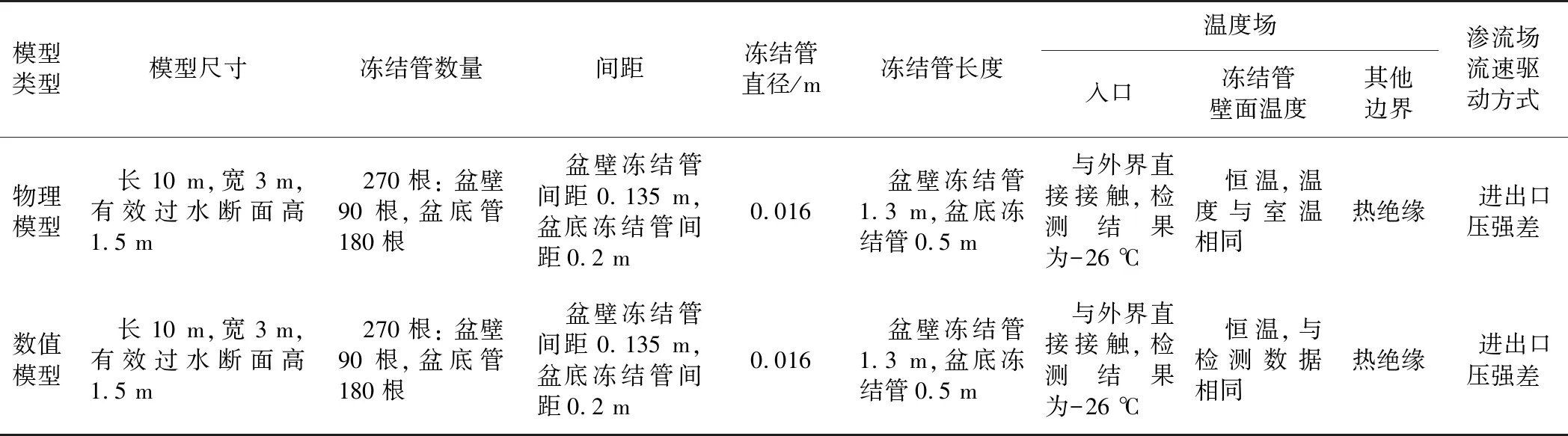
表4 物理模型、数值模型的参数及边界条件

图11 冻结管分布物理模型
模型试验采用多场耦合有限元软件Comsol Multiphysics,在对模型试验进行验证的同时,进一步观察冻结温度场的变化。数值模型为多场耦合模型,网格在冻结管附近进行局部细化。数值模拟材料热力学参数见表5。

表5 数值模拟材料热力学参数
数值模拟的盆形冻结结构见图12。从图12可以看出,在渗流条件下,采用盆形冻结布管方式能够形成完整的盆形结构,有效隔绝内外水力联系。
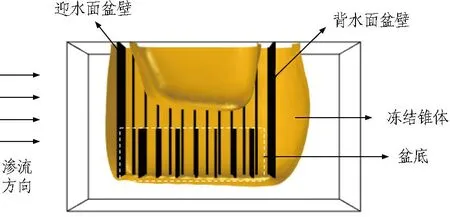
图12 数值模型的盆形冻结结构
根据相似原理,当实际工程渗流速度为0.5 m/d时,物理模型试验渗流速度为5 m/d。盆形结构的3个关键截面的冻结发展过程见图13。物理模型试验过程的关键节点5、10、15、20 h,分别代表实际工程的20、40、60、80 d。从对比结果来看,所建数值模型能够有效反映盆形冻结的发展过程,可以对冻结温度场的发展进行有效预测。

(a) 盆底下端面(t=20 d) (b) 盆底下端面(t=40 d) (c) 盆底下端面(t=60 d) (d) 盆底下端面(t=80 d)

(e) 盆底上端面(t=20 d) (f) 盆底上端面(t=40 d) (g) 盆底上端面(t=60 d) (h) 盆底上端面(t=80 d)

(i) 盆壁上端面(t=20 d) (j) 盆壁上端面(t=40 d) (k) 盆壁上端面(t=60 d) (l) 盆壁上端面(t=80 d)
模型试验结束后,根据温度测点的结果开挖掉多余土体之后最终形成的盆形结构(单侧)如图14所示,从图中可以明显地看出盆壁及盆底部分,由此认为盆形冻结能够形成有效的冻结止水结构,方案可行。

图14 物理模型试验箱内的盆形冻结结构
4 盆形冻结施工控制技术
通过数值模拟和物理模型试验的结果可以发现,冻结的发展表现出明显的阶段性规律。盆底的冻结在背水面先形成冻结体,并逐步发展至迎水面,最终全部冻结管交圈。基于此,本节针对盆形冻结的积极冻结期和维护冻结期,通过分析冻结特点,提出2个阶段盆形冻结施工控制技术。
4.1 积极冻结期的群孔布置技术
多排管冻结与单管冻结发展过程并不相同,这种现象可称为群孔效应。具体是指,在施工过程中,采用多排管冻结,冻结的发展与冻结管所处环境相互作用,共同促进冻结体形成的过程。
对于具体的冻结工程,环境因素如地下水温度等无法改变。本次数值模拟仅考虑冻结管间距、土体导热系数、渗流速度3个敏感因素。将模拟结果整理到如图15所示的坐标系中,可以构建一个有效冻结边界面,边界面下方的点都可以作为边界条件在多排管冻结时发生有效的群孔冻结现象。
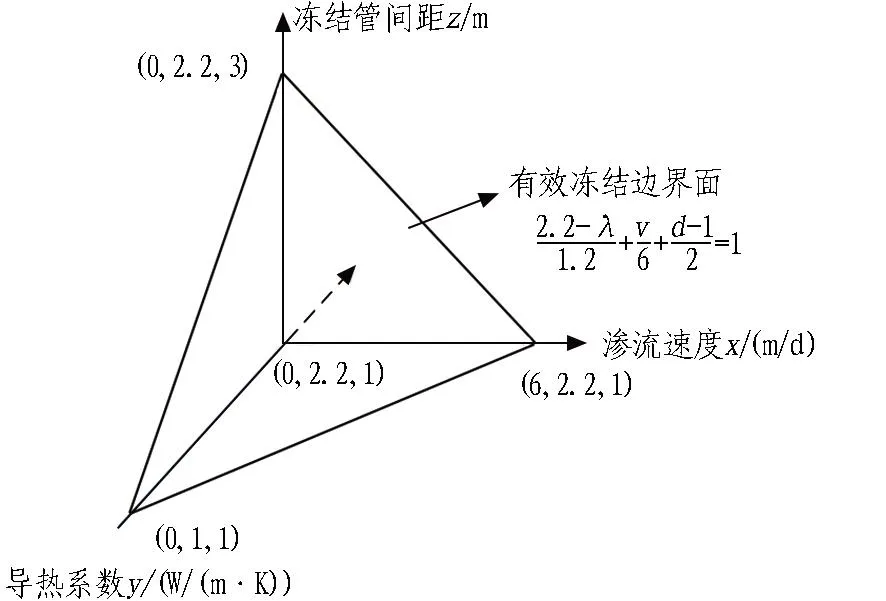
图15 有效冻结边界面
整理得到有效冻结边界面的方程为:
(13)
式中:d为冻结管间距,m;λ为土体等效导热系数,W/(m·K);v为渗流速度,m/d。
当确定地下水渗流速度及土体等效导热系数后,可以得到设计间距
(14)
4.2 维护冻结期的精细化控制技术
在冻结工程的积极冻结期,使用设备的最大制冷能力使地层尽快达到冻结厚度与冻结强度。而维护冻结期则是在工程施工阶段,只需维护已经成形的冻结结构保持稳定并不再扩展。传统冻结工程常常采用降低冷媒温度或流速的方法对冻结体进行维护[21]。当冻结管壁面温度升高5 ℃时可以节约8%~10%的电能输入;而当冻结管较多时,可以采用切割部分冻结管的方法,在对冻结体进行维护的同时,释放一部分工作区域,有效达到节约能源的目的。
针对渗流条件下处于维护阶段的盆形冻结提出以下2种冻结管切割方式: 1)隔排切割冻结管; 2)仅保留盆壁冻结管。盆形冻结维护方式如图16所示。分析过程中仅取整个盆形对称结构右侧的冻结管部分。

(a) 隔排切割冻结管
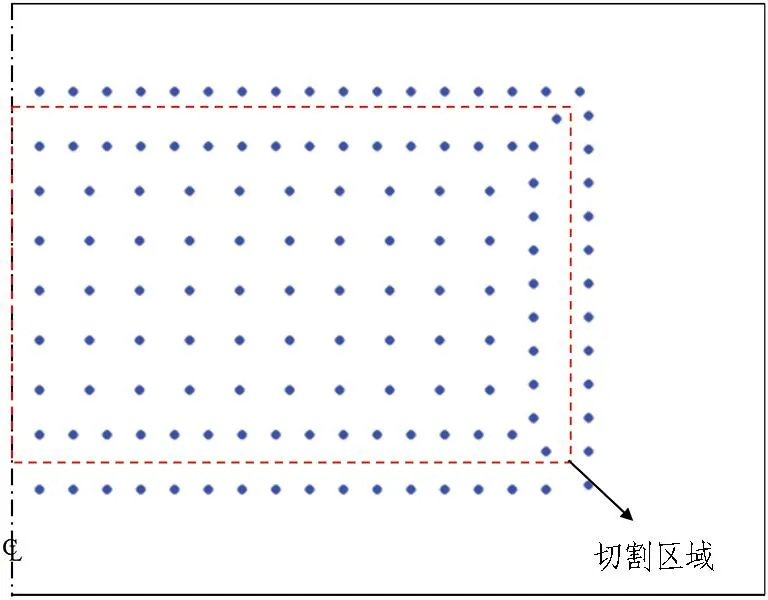
(b) 仅保留盆壁冻结管
2种维护方式下,盆形结构各关键截面的冻结形态变化如图17—18所示。
从图17中可以看出,从隔排冻结管被切割、冻结工程进入维护冻结期开始,整个截面的温度场自迎水面向背水面逐渐降低。迎水面在积极冻结期所形成的锯齿形结构持续存在,但由于冷量供给减少,迎水面附近冻结体温度升高,角点附近冻结体消融,是迎水面维护的薄弱位置。盆底中轴面由于仅有迎水面与外界接触,因而受到渗流作用影响很小。盆壁上端面在迎水面与背水面一侧由于冻结管数量与积极冻结期相比未发生变化,其冻结效果与温度场分布也未有明显变化;在顺水流一侧,尽管2/3的冻结管被切除,在剩余冻结管供冷的条件下,依然能够维持盆壁结构。
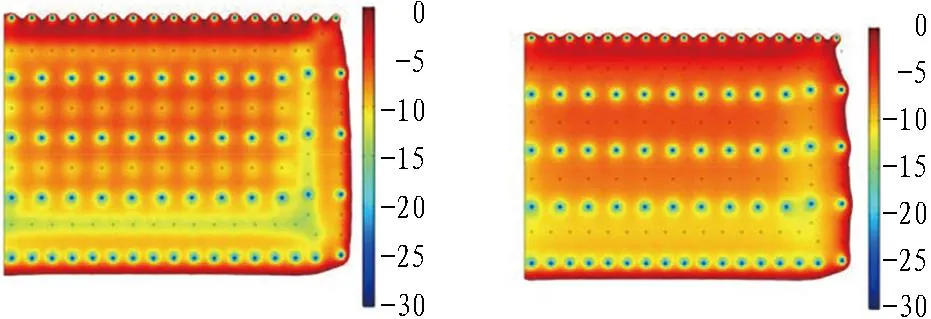
(a) 盆底下端面(t=10 d) (b) 盆壁下端面(t=40 d)
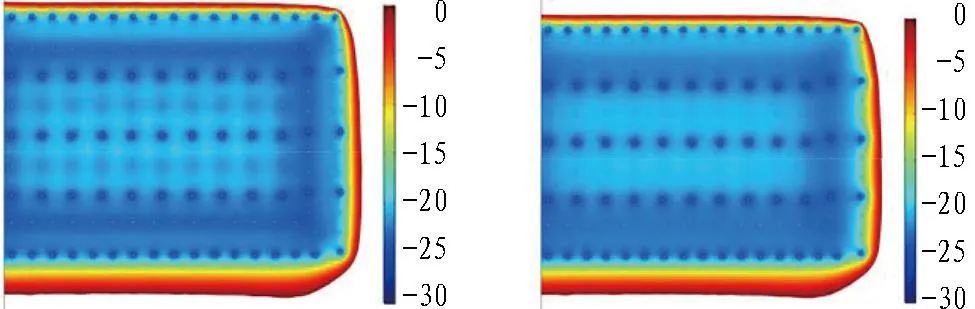
(c) 盆底中轴面(t=10 d) (d) 盆壁中轴面(t=40 d)
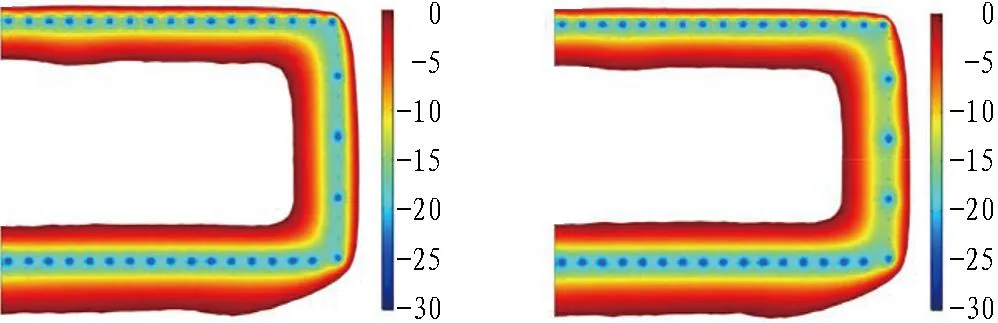
(e) 盆壁上端面(t=10 d) (f) 盆壁上端面(t=40 d)
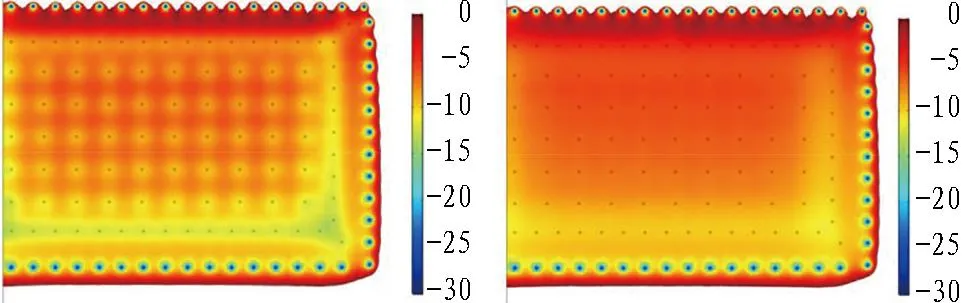
(a) 盆底下端面(t=10 d) (b) 盆底下端面(t=40 d)
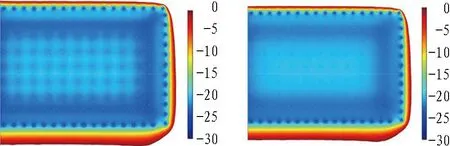
(c) 盆底中轴面(t=10 d) (d) 盆底中轴面(t=40 d)
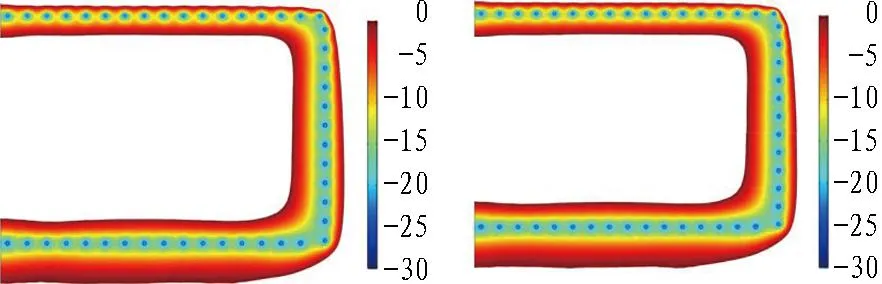
(e) 盆壁上端面(t=10 d) (f) 盆壁上端面(t=40 d)
从图18中可以看出,采用仅保留盆壁冻结管的维护方式时,在维护冻结期迎水面盆壁保持了锯齿形的形态,盆底内部冻结场温度逐渐均一化,整个截面的温度场自迎水面向背水面逐渐降低,截面冻结形态保持稳定。盆壁上端面温度场的发展与积极冻结期非常相似,在整个维护阶段,截面冻结形态保持稳定。
根据分析,当采用隔排切割冻结管的方法时,能源节约率约为50%,而采用仅保留盆壁冻结管的方法时,能源节约率则与盆壁和盆底冻结管的数量n有关。相同工程条件下,可以根据式(15)对冻结维护方式进行选择。
(15)
式中:r为盆底冻结管列数;w为盆底冻结管排数;ρ为盆底冻结管与盆壁冻结管间距系数,即
d底=ρ·d壁。
(16)
因此,当r·w≥2ρ(r+w)时,可优先采用仅保留盆壁冻结管的维护方法。
针对冻结工程的维护过程,能源节约比例、冻结体的完整性、施工操作空间的大小,都应该是需要考虑的因素。本次研究所采用的2种维护方式,即仅保留盆壁冻结管和隔排切割冻结管的方法,都可以有效满足盆形结构维护期的冷量供给,保持完整的盆形形态。其中,仅保留盆壁冻结管的维护方法可以提供更大的施作空间,是工程中应该首先考虑的方法。
4.3 冻结三维实时监测平台
人工冻结施工是一个随时间变化的复杂动态的过程。冻结性状受到制冷系统运行状况、地质条件、边界散热、施工工况等诸多因素的影响。即时监测冻结工程状态,反馈冻结施工情况,对冻结过程进行即时管控,方可规避冻结工程风险。
冻结工程监测平台系统功能如图19所示。
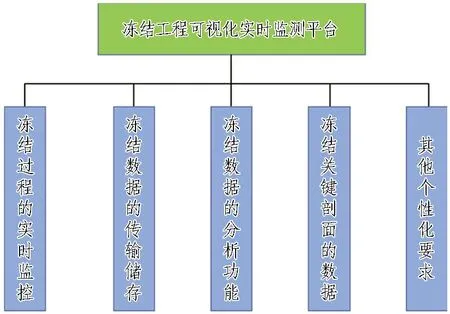
图19 三维实时监测平台功能
该平台可以实现冻结过程的实时监控,将冻结工程中温度传感器、渗压计测得的对应位置的温度、水压力实时反馈,得到每个测点的时程曲线,即时获取冻结工程状态,对冻结参数进行调整控制。图20示出了某一具体时刻各测点的冻结状态。

图20 冻结温度实时监测
5 结论与展望
5.1 结论
盆形冻结止水技术是冻结技术在城市地下工程的创新应用。本文通过分析研究砂卵石冻结体物理力学特征、盆形冻结各阶段的冻结过程,主要得到以下结论:
1)冻结砂卵石的破坏形态以剪切破坏为主,高围压、低负温时易出现体胀型破坏。其长期强度与瞬时强度的比值为0.23~0.42。基于损伤理论建立了冻结砂卵石全过程蠕变模型,并得到了良好的拟合效果。
2)荷载对冻胀率及融沉系数影响最大,细粒土质量分数次之。细粒土质量分数小于0.82%的无载饱和砂卵石是弱冻胀材料。建立了考虑砂卵石冻胀率及融沉系数的三维预测模型。
3)根据物理模型试验和数值模拟的结果,盆形冻结可以在地下水渗流条件下形成完整的盆形结构,起到止水的效果。
4)盆底冻结管在冻结过程中表现出与单管冻结迥异的“群孔效应”,根据试验结果提出了包含冻结管间距、土体导热系数、渗流速度3因素的积极冻结期冻结管合理间距的确定与布置技术。
5)为节约维护冻结期的能源,提出了隔排切割冻结管、仅保留盆壁冻结管2种形式以对冻结区域进行精细化控制。经过分析,2种方式均可以有效满足盆形结构维护期的冷量供给,保持了完整的盆形形态。
5.2 展望
随着城市浅部地下空间资源的开发殆尽,各大城市的地下空间开发将逐步进入地层深部,未来城市深层地下空间开发将逐步常态化,地下水问题对于地下工程而言是必须要解决的问题。本文所研究的“盆形冻结”技术,具有不抽取地下水、不破坏地下水运移路径、不污染地下水环境等优点,有良好的市场应用前景,推广价值显著。
