高原水电站地基深厚覆盖层渗透特性分析

祁诗渊，张玉云，陈 亮，李家欢

(1.西藏农牧学院水利土木工程学院，西藏 林芝 860000；2.西藏农牧学院西藏土木水利电力工程技术研究中心，西藏 林芝 860000)

藏东南高山河谷区蕴藏着极为丰富的水能资源。其中，雅鲁藏布江是中国最长的高原河流，位于西藏自治区境内，也是世界上海拔最高的大河之一。水能蕴藏量丰富，干流与五大支流的天然水能蕴藏量近1亿kW，在中国仅次于长江。目前，雅鲁藏布江下游正在开发，已建成的水电站都存在深厚覆盖层。如西藏雅鲁藏布江林芝多布水电站工程，主要任务为发电，兼顾灌溉。西藏尼洋河多布水电站建筑物区覆盖层深厚，河床及左岸为超深厚复杂覆盖层，左岸台地覆盖层厚180～3593m，河床覆盖层左深右浅，左岸一般厚60～180m，右岸覆盖层厚度16～50m[1]。

西藏林芝市老虎嘴水电站工程，其工程规模为中型，主要水工建筑物级别为3级；次要水工建筑物级别为4级[2]。左岸台地地面高程3298～3340m，覆盖层厚105～174m，最深206.5m，其中左岸副坝坝基覆盖层厚16～28～109m[3]。

目前，前人对深厚覆盖层渗透稳定问题的研究并不系统和深入，多数都集中于不同因素对试样渗透特性的影响[4]。张家发[5]等采用室内试验模拟了渗透破坏的全过程，得出悬挂式防渗墙对防渗效果并不显著的结论；陈群[6]等研究比较了最大粒径和细颗粒含量不同的缺级试样土条件下对应的管涌渗透规律；罗玉龙[7]等进行了大量不同应力状态下堤基砂砾石层的管涌破坏机理试验研究，并提出临界渗透坡降经验公式；詹美礼[8]等建立了堤坝饱和-非饱和渗流系统，进行了土样的非饱和导水率试验以及堤坝在不同水位变化工况下的非饱和渗流试验研究；王璠[9]也通过大尺度流固耦合试验对深厚覆盖层上建坝地基内管涌发生-发展-破坏的全过程进行分析研究，准确描述了不同阶段试样内部水压力和渗透梯度对应的不同变化规律。

上述研究均基于当地的土进行的，但学者们对青藏高原坝基深厚覆盖层粗粒土的渗透规律鲜有研究。本研究的内容是探索高山河谷区覆盖层特定土体的渗透特征。具体内容包括以颗粒大小不同的两种颗粒为基本级配，通过筛分试验、击实试验、颗粒分析试验，渗透试验等来研究二元颗粒配比的渗透特征，收集颗粒大小组成、填筑密度、渗透系数与二元颗粒的粒径比、水力坡降、孔隙比等数据，分析了水流入渗过程中的影响因素，并最终推导出经验公式，为进一步揭示藏东南地区深厚覆盖层渗透侵蚀规律和预防管涌、流土灾害提供试验依据。

1 试验设备及试验方案

1.1 TST-70型渗透仪简介

试验平台所用的试验设备为TST-70型渗透仪，用以完成常水头渗透试验。部分设备参数见表1，设备具体如图1所示。

图1 TST-70型渗透仪

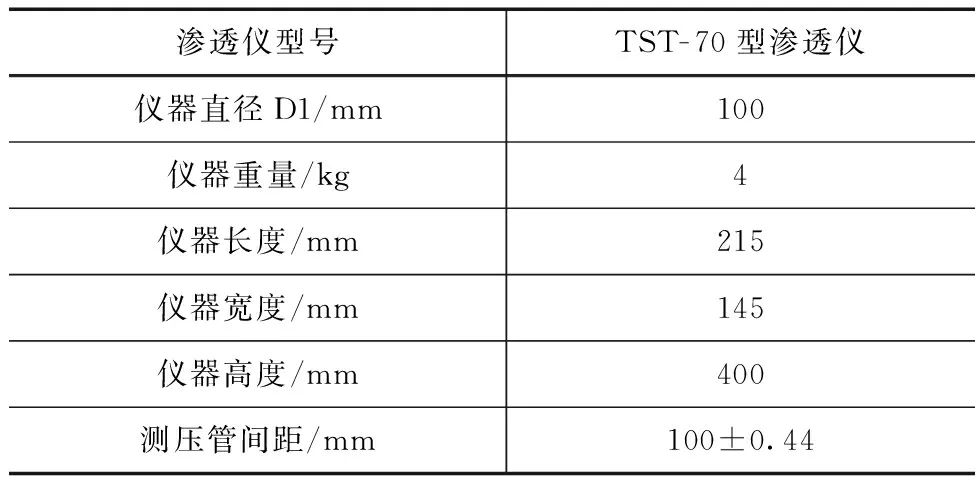
表1 渗透仪参数表

表2 土体粒径级配(样本)

1.2 试验方案

通过查阅大量文献及试验室之前的研究成果，确定采用常水头试验模拟水流对不同土体的渗透性，并对采用的高山河谷区深厚覆盖层不同级配的粗颗粒土样进行筛分、渗透，击实试验，确定其粒径级配、渗透系数及最大干密度等参数，得出抗渗性能最强的颗粒粒组。

通过数据处理软件Microsoft Excel对上述试验结果进行数据分析，得出不同级配土体的渗透系数，并对渗透系数曲线进行回归拟合以及数值分析，得出相应的渗透规律，为西藏雅鲁藏布江水电站及大坝的开发和安全运行提供相应的数据和理论支持。

本次常水头渗透试验的原材料采用5种不同粒径的高山河谷区深厚覆盖层不同级配的粗颗粒土样，代号分别为A、B、C、D、E，通过将前4种颗粒(A、B、C、D)按不同比例(如1∶1，1∶2，2∶1，1∶4，4∶1)混合，形成30种组合的二元颗粒，本试验旨在通过测定不同二元颗粒组合的渗透特征及渗透参数，并拟合数据曲线得出相关的经验公式，比较得出抗渗性能最强的一组二元颗粒组合。A为中砾粒组，B为细砾粒组，C为粗砂粒组，D为中砂粒组，E为细砂及粉粒组的混合土。本试验主要在于研究前4种不同颗粒级配的渗透特性。土体粒径级配(样本)见表二，土体的粒径级配曲线如图2所示。

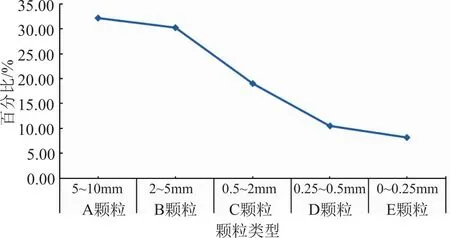
图2 土体的粒径级配曲线

从图2的土体粒径级配曲线可以看出，土体中中砾粒组含量最多，5～10mm粒组占30%～35%，而细砂及粉粒组的混合土的含量最少，0～0.25mm占5%～10%。粒径级配曲线是连续的，即本次试验土体为连续性土。

常水头渗透试验原理就是在试验装置中测出渗流量、水位差，从而计算出渗流速度和水力梯度。二元颗粒配比方案见表3—4。

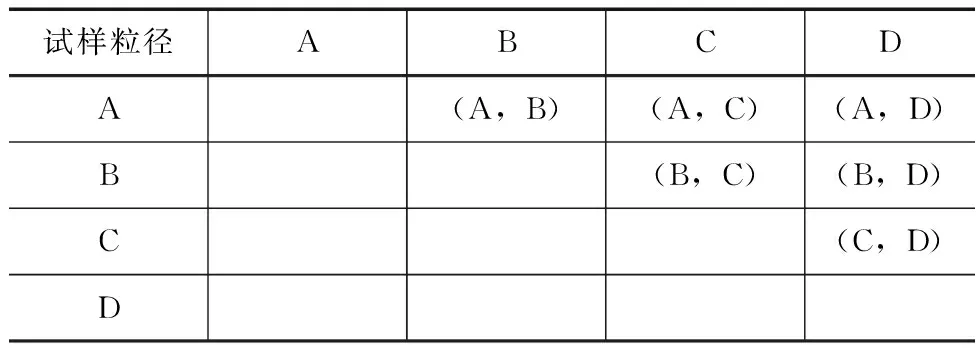
表3 二元颗粒组合

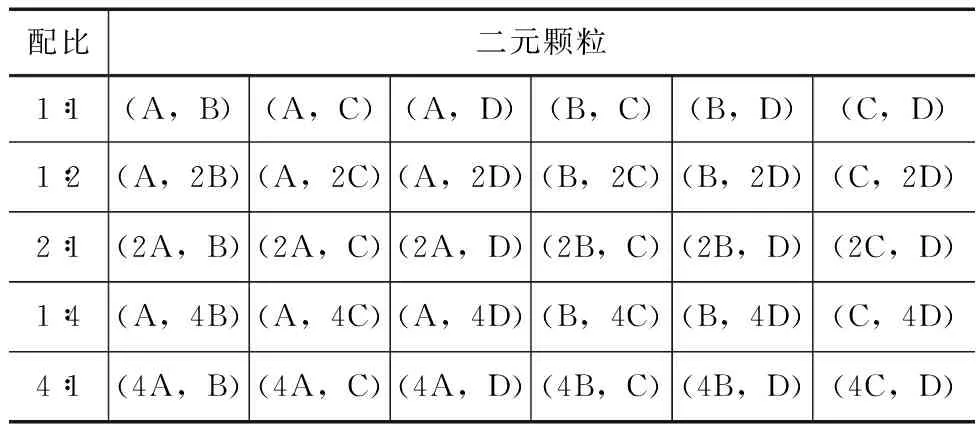
表4 二元颗粒的混合配比

2 常水头渗透试验结果及分析

2.1 数据处理

根据需要可装数个不同孔隙比的试样进行渗透系数的测定。常水头渗透试验渗透系数计算公式为：

(1)

(2)

式中，KT—水温T℃时试样的渗透系数，cm/s；Q—时间t秒内的渗透水量，cm3；L—渗径，cm，等于两测压孔中心间的试样高度；A—试样的断面积，cm2；t—时间，s；H1、H2—水位差，cm；K20—标准温度(20℃)时试样的渗透系数，cm/s；ηT—T℃时水的动力粘滞系数，10-6kPa·s；η20—20℃时水的动力粘滞系数，10-6kPa·s；e—孔隙比，%。

当进行不同孔隙比下的渗透试验时，可在半对数坐标上绘制以孔隙比为纵坐标，渗透系数为横坐标的e-k关系曲线图。

2.2 试验结果及分析

通过常水头渗透试验得出的试验结果见表5，全部工况的二元颗粒组合渗透系数的折线统计如图3所示。

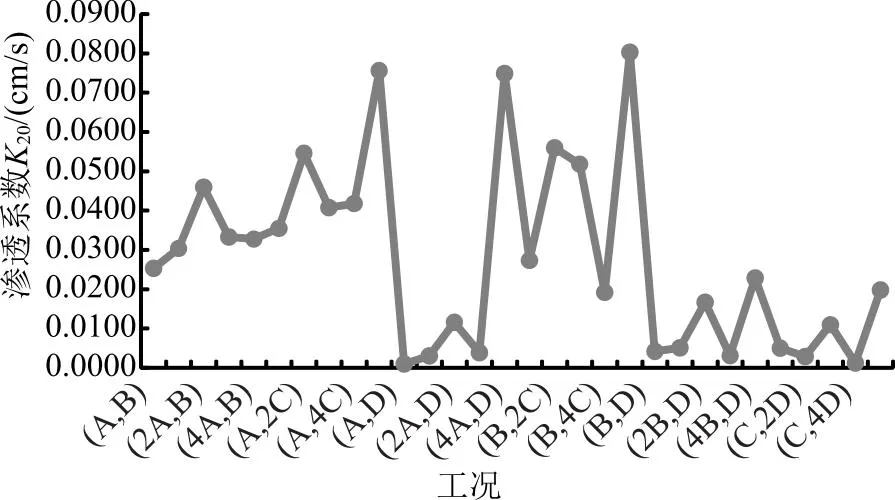
图3 渗透系数折线统计图

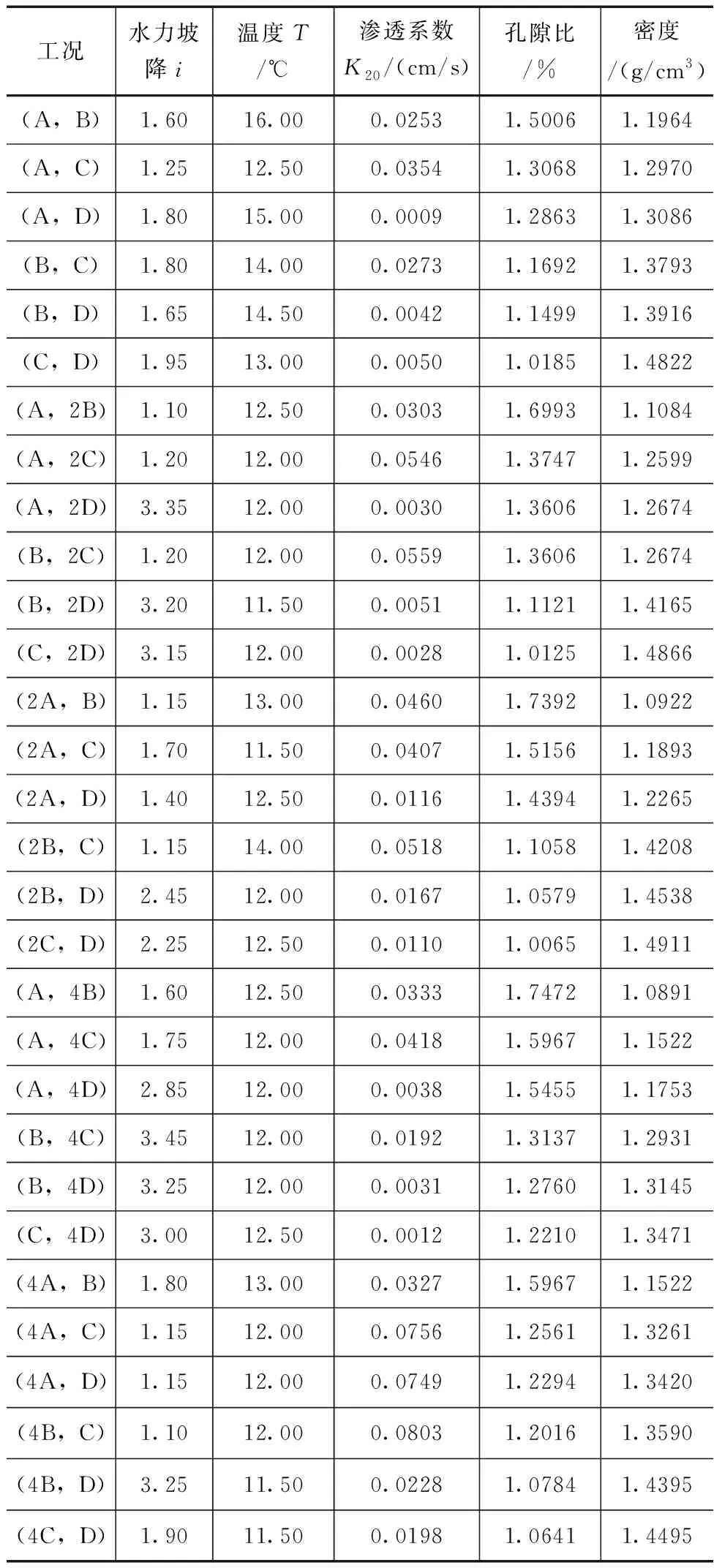
表5 渗透试验结果

综上所述，从表5可以得出，在以上30种二元颗粒组合中，(A，D)组合的渗透系数最小，其值为0.0009cm/s，因此这组二元颗粒组合的抗渗性能是最强的，说明中砾和中砂的混合土体的抗渗性能最强。

因此，在未来西藏林芝地区研发设计水利工程，例如大坝等设施时，大坝防渗墙的深厚覆盖层可以选择高山河谷区深厚覆盖层不同级配下的粗颗粒土样中的中砾粒组和中砂粒组的混合二元颗粒，这种混合土对于渗流侵蚀破坏的防护作用非常大，可以有效地避免潜蚀和管涌及流土等对大坝具有巨大破坏性的危害现象。图4—15为常水头渗透试验统计图，即渗透试验在不同配比的土样下对不同变量所做出的散点图关系。

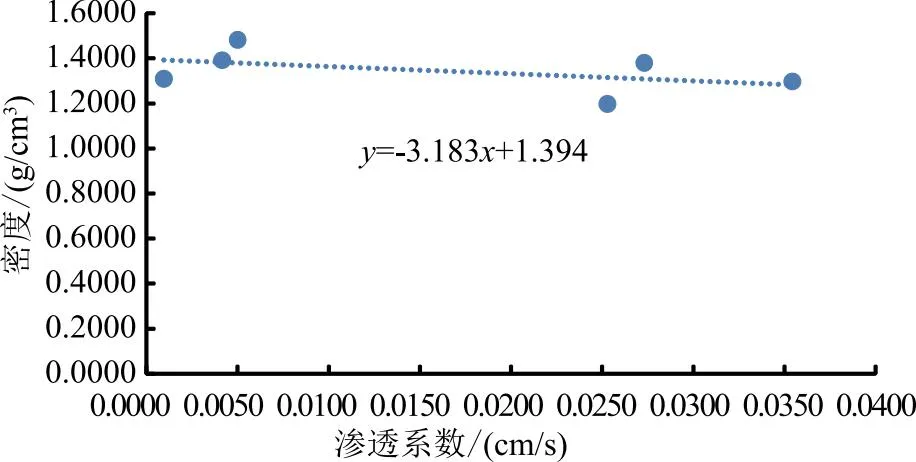
图4 1∶1配比下渗透系数-密度散点图

2.2.1渗透系数-密度散点图

不同工况下二元颗粒组合的渗透系数-密度散点图的函数关系如图4—6所示。

从图4中可以看出，在1∶1的配比下，当密度为1.3086时，渗透系数最小，为0.0009，即(A，D)组合。当密度为1.2970时，渗透系数最大，为0.0354，即(A，C)组合。

从图5中可以看出，在2∶1的配比下，当密度为1.4538时，渗透系数最小，为0.0110，即(2B，D)组合。当密度为1.2265时，渗透系数最大，为0.0518，即(2A，D)组合。

从图6中可以看出，在4∶1的配比下，当密度为1.4495时，渗透系数最小，为0.0198，即(4C，D)组合。当密度为1.3590时，渗透系数最大，为0.0803，即(4B，C)组合。

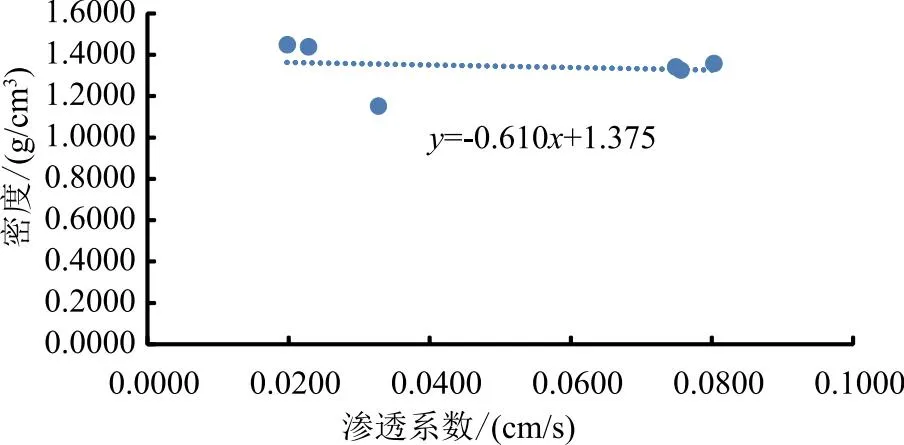
图6 4∶1配比下渗透系数-密度散点图

从图4—6中我们可以看出，渗透系数和密度之间存在函数关系，二者呈现负相关的关系，即随着二元颗粒组合密度的增加，渗透系数逐渐变小，抗渗性能逐渐变强，这一现象的原因是随着二元颗粒组合密度的增加，颗粒间的孔隙比逐渐减小，水流渗透侵蚀变得更加困难，因此水流穿过土体渗透侵蚀产生的流量逐渐变小，即渗透系数变小，抗渗性能变强。另外，在二元颗粒配比2∶1的比例下，渗透系数-密度的函数关系变化最明显。

2.2.2渗透系数-孔隙比散点图

不同工况下二元颗粒组合的渗透系数-密度散点图的函数关系如图7—9所示。

从图7中可以看出，在1∶1的配比下，当孔隙比为1.2863时，渗透系数最小，为0.0009，即(A，D)组合。当孔隙比为1.3068时，渗透系数最大，为0.0354，即(A，C)组合。

从图8中可以看出，在1∶2的配比下，当孔隙比为1.1025时，渗透系数最小，为0.0028，即(C，2D)组合。当孔隙比为1.3606时，渗透系数最大，为0.0559，即(B，2C)组合。

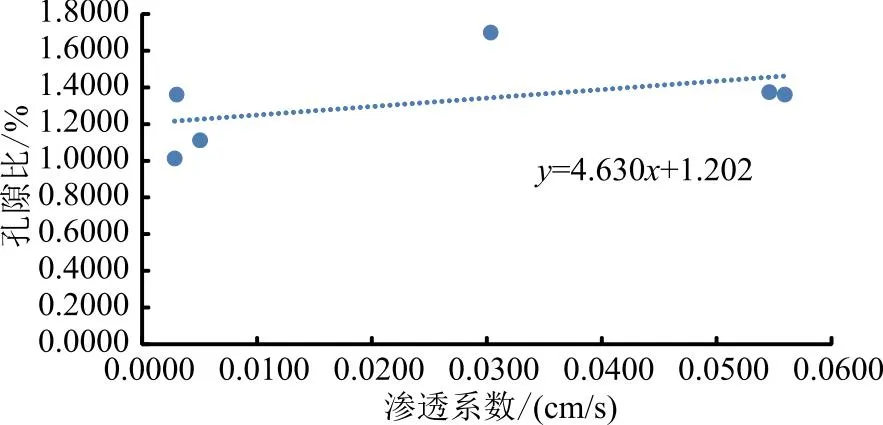
图8 1∶2配比下渗透系数-孔隙比散点图

从图9中可以看出，在1∶4的配比下，当孔隙比为1.2210时，渗透系数最小，为0.0012，即(C，4D)组合。当孔隙比为1.5967时，渗透系数最大，为0.0418，即(A，4C)组合。

图9 1∶4配比下渗透系数-孔隙比散点图

从图7—9中可以看出，渗透系数和孔隙比之间存在函数关系，二者大多数情况下整体呈现正相关的关系。即随着二元颗粒组合孔隙比的增加，渗透系数逐渐变大，抗渗性能逐渐变弱，这一现象的原因是随着二元颗粒组合孔隙比的增加，土体的孔隙逐渐增大，水流渗透侵蚀变得更加容易，因此水流穿过土体渗透侵蚀产生的流量逐渐变大，即渗透系数变大，抗渗性能变弱。另外，在二元颗粒配比1∶4的比例下，渗透系数—孔隙比的函数关系变化最明显。

2.2.3水力坡降-孔隙比散点图

不同工况下二元颗粒组合的渗透系数—密度散点图的函数关系如图10—12所示。

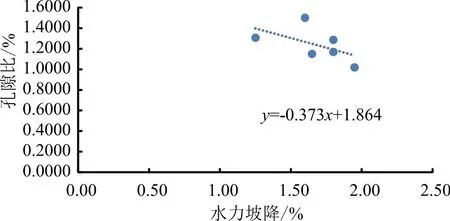
图10 1∶1配比下水力坡降-孔隙比散点图

从图10中可以看出，在1∶1的配比下，当孔隙比为1.3068时，水力坡降最小，为1.25，即(A，C)组合。当孔隙比为1.0185时，水力坡降最大，为1.95，即(C，D)组合。

从图11中可以看出，在1∶2的配比下，当孔隙比为1.6993时，水力坡降最小，为1.10，即(A，2B)组合。当孔隙比为1.3606时，水力坡降最大，为3.35，即(A，2D)组合。

图11 1∶2配比下水力坡降-孔隙比散点图

从图12中可以看出，在1∶4的配比下，当孔隙比为1.7472时，水力坡降最小，为1.60，即(A，4B)组合。当孔隙比为1.3137时，水力坡降最大，为3.45，即(B，4C)组合。

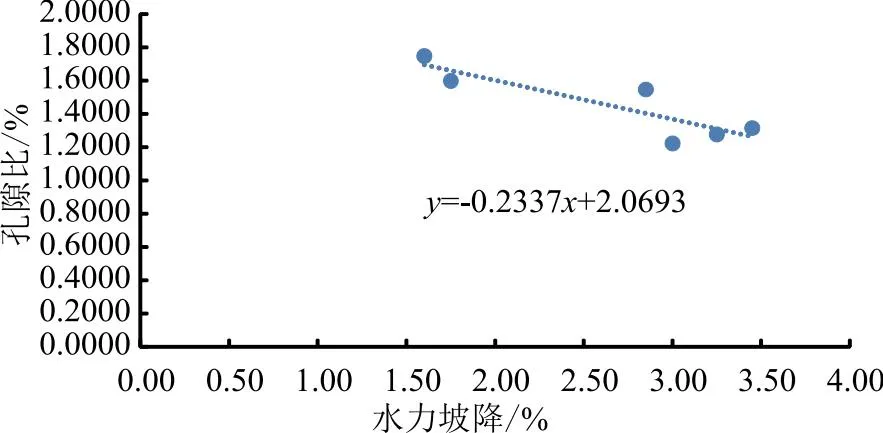
图12 1∶4配比下水力坡降-孔隙比散点图

从图10—12中可以看出，水力坡降和孔隙比之间存在函数关系，二者呈现负相关的关系，即横坐标是水力坡降值，纵坐标是孔隙比值，即随着孔隙比的增加，二元颗粒组合水力坡降逐渐变小，抗渗性能逐渐变弱，这一现象的原因是随着二元颗粒组合孔隙比的增加，颗粒间的孔隙逐渐增大，水流渗透侵蚀变得更加容易，因此水流穿过土体渗透侵蚀产生的流量逐渐变大，即渗透系数变大，水力坡降变小，抗渗性能变弱。另外，在二元颗粒配比1∶1的比例下，水力坡降-孔隙比的函数关系变化最明显。

2.2.4水力坡降—密度散点图

不同工况下二元颗粒组合的水力坡降-密度散点图的函数关系如图13—15所示。

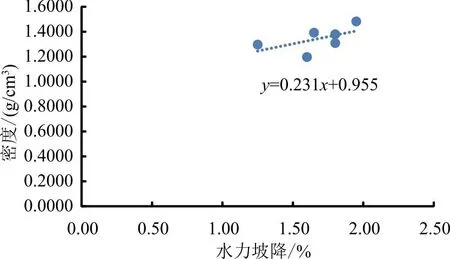
图13 1∶1配比下水力坡降-密度散点图

从图13中可以看出，在1∶1的配比下，当密度为1.2970时，水力坡降最小，为1.25，即(A，C)组合。当密度为1.4822时，水力坡降最大，为1.95，即(C，D)组合。

从图14中可以看出，在1∶1的配比下，当密度为1.2970时，水力坡降最小，为1.25，即(A，C)组合。当密度为1.4822时，水力坡降最大，为1.95，即(C，D)组合。

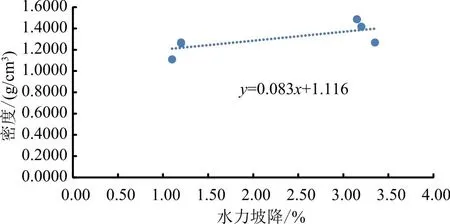
图14 1∶2配比下水力坡降-密度散点图

从图15中可以看出，在1∶4的配比下，当密度为1.0891时，水力坡降最小，为1.60，即(A，4B)组合。当密度为1.2931时，水力坡降最大，为3.45，即(B，4C)组合。

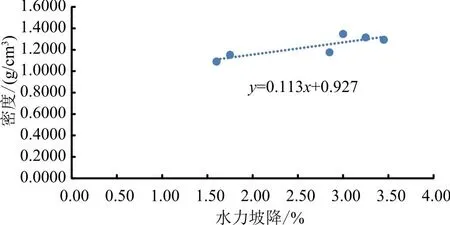
图15 1∶4配比下水力坡降-密度散点图

从图13—15中可以看出，水力坡降和密度之间存在函数关系，二者呈现正相关的关系，即横坐标是水力坡降值，纵坐标是密度值，即随着密度的增加，二元颗粒组合水力坡降逐渐变大，抗渗性能逐渐变强，这一现象的原因是随着二元颗粒组合密度的增加，颗粒间的孔隙逐渐变小，水流渗透侵蚀变得更加困难，因此水流穿过土体渗透侵蚀产生的流量逐渐变小，即渗透系数变小，水力坡降变大，抗渗性能变强。另外，在二元颗粒配比1∶1的比例下，水力坡降-密度的函数关系变化最明显。

3 结论

本文基于常水头渗透试验，获得了不同二元颗粒组合的渗透参数。结果表明：当水力梯度较小时，随着水力梯度的增大，渗透系数逐渐减小；粗砂中水力梯度对渗透系数影响最大，中砂次之，细砂对渗透系数的影响最小。土体的密度如果越大，土体的抗渗性能越强，土体的孔隙比越大，抗渗性能越弱。从中可以得出高原深厚覆盖层的渗透系数与密度，孔隙比之间的函数关系以及经验公式，为雅鲁藏布江下游流域的后续水电开发提供有力的科学依据。由于高原不同大坝的深厚覆盖层存在差异，因此，研究结果应用尚需进一步研究。