高阶SF-SFDTD 方法在含时薛定谔方程求解中的应用研究*
2024-02-21谢国大潘攀任信钢冯乃星方明李迎松黄志祥
谢国大 潘攀 任信钢 冯乃星 方明 李迎松 黄志祥†
1) (安徽大学电子信息工程学院,合肥 230601)
2) (安徽大学,智能计算与信号处理教育部重点实验室,合肥 230601)
1 引言
计算电磁学在当今各种电子设备中电磁效应(辐射、散射或传播)的建模和仿真中占据重要地位[1,2].其应用包括但不限于通信、生物成像和诊断、电磁兼容性或干扰、信号完整性分析等领域[3,4].近年来,由于现代电子技术的飞速发展,集成电路相关元器件的特征尺寸已经缩小到纳米级别,这大大提高了单位体积内物质存储和信息处理的效率,为智能化、小型化电子设备的发展提供了强有力的支持[5,6].又因为纳米器件本身尺寸极小,结构中粒子的量子效应明显,这导致基于经典电磁理论的建模方案难以描述微观粒子的量子特性.另外,采用实验方法直接测量器件的各种性能又十分困难,且成本较高.因此,如何准确、高效地研究纳米器件的相关特性,已成为当今纳米器件建模和设计的关键挑战.
对于分析大部分纳米器件的特性,确定器件结构电子的本征值和本征态是一个重要的切入点.例如,在研究弹道输运时,需要考虑传导通道的横向本征态,这一点与非平衡格林函数密切相关[7].此外,微观电子传输中本征态的激发或不同本征态之间的相互作用,会产生各种有趣的现象,如Fano共振[8]、共振隧穿效应[9]等.因此,准确而有效地计算纳米结构中的本征态和特征频率对理解微纳结构系统中各种微观现象的物理机制和优化器件性能起着重要作用.而薛定谔方程可以描述物质粒子的运动和特性,通过数值求解薛定谔方程,可以确定纳米器件的本征值与本征态,这就使得薛定谔方程的数值解变得越来越重要[7].在时间和空间上具有二阶数值精度的时域有限差分(finite-difference time-domain,FDTD(2,2))方法被证明是求解含时薛定谔方程的最有效和最简单的方法之一[10,11].这是因为FDTD(2,2)方法无需对薛定谔方程作进一步的推导,只需要直接对控制方程中的时间和空间偏导项进行中心差分离散,最后导出数值迭代公式.然而,FDTD(2,2)方法在时间和空间上只具有二阶精度,在长时间的数值迭代中产生较大的误差累计,导致仿真结果不正确或与理论结果差距较大.另外,FDTD(2,2)方法中时间步长的取值范围受时间稳定性条件的影响,即最大时间步长受计算区域中网格尺寸大小的限制,这极大地限制了采用FDTD(2,2)方法求解薛定谔方程的计算效率.
为了克服传统FDTD(2,2)方法数值色散大的问题,一些高阶FDTD(2,4)方法被应用于求解含时薛定谔方程[12,13],数值计算误差有明显改善.然而高阶FDTD(2,4)方法对控制方程的离散是一种非辛离散形式,在长时间的数值仿真中难以保证系统的能量守恒特性.由于薛定谔方程的时间演化,本质上是归一化波函数的多次旋转.文献[14]提出了采用高阶辛FDTD(3,4) (symplectic finitedifference time-domain,SFDTD(3,4))方法求解含时薛定谔方程,所推导出来的辛算子具有对称属性,确保离散方程在时间演化过程中保持能量守恒,没有幅度误差.然而,高阶辛FDTD(3,4)方法也是一种显式迭代算法,虽然具有比传统FDTD方法更宽松的Courant-Friedrichs-Lewy (CFL)稳定性条件[15],但计算效率有待进一步的提高.为了突破CFL 稳定性条件的限制,一些隐式无条件稳定的FDTD 方法被开发出来并用于薛定谔方程的数值求解,但隐式算法往往需要对控制方程进行特殊的离散处理及繁琐的公式推导和数值计算: 包括对时间偏导数的隐式离散、时间步长分裂处理及矩阵求逆计算等.另外,采用较大的时间步长会导致隐式FDTD 方法的数值色差较大,在实际应用中,需要根据实际的计算需求选择合适的时间步长来平衡计算精度和计算效率.
鉴于传统FDTD(2,2)方法及其优化算法在计算效率和计算精度两方面所存在的问题,本文提出了一种稳定性条件可控的空间滤波(spatial filtering)-SFDTD(3,4)(SF-SFDTD(3,4))方法.在SFDTD(3,4)方法中采用不满足稳定性条件的时间步长会导致空间频域中高频电磁分量幅值呈现指数倍增长并导致数值结果发散,因此,在数值迭代过程中采用空间滤波方法[16–18]能够有效地滤除这些不稳定的高频分量,保证计算结果的稳定性.又因为当时间步长的取值满足CFL 稳定性条件时,高频分量的幅值几乎零,因此对计算结果的精确性影响较小.采用不满足CFL 稳定性条件的时间步长导致高频分量的幅值增加,但这一结果只会影响计算结果的稳定性,滤除这些不稳定的高频分量几乎不会对计算结果的精度造成影响.另外,SF-SFDTD(3,4)方法与传统SFDTD(3,4)方法采用相同的迭代公式,只需要在每一次的数值迭代过程中加入滤波操作.因此,它保留了传统SFDTD(3,4)方法的简洁性和有效性,同时提高了计算效率.
论文的组织结构如下: 第2 节介绍了基于含时薛定谔方程的SF-SFDTD(3,4)方法的基本原理,包括扩展SFDTD(3,4)方法的CFL 条件限制,归一化低通滤波器半径的定义及滤波处理过程,第3节给出了SF-SFDTD(3,4)方法的数值色散分析,第4 节通过几种典型的数值算例来验证SF-SFDTD(3,4)方法的正确性和有效性.最后给出本文工作的总结与展望.
2 方 法
2.1 SFDTD 方法求解薛定谔方程的迭代公式
具有静态电位V(r,t)=V(r)的含时薛定谔方程表达式为[9]
其中ψ是与空间r和时间t有关的波函数,m*是粒子的质量是哈密顿算符.为避免在数值计算中使用复数,将ψ(r,t) 分解为实分量和虚分量,即:
将(2)式代入(1)式中,得到以下方程组:
根据文献[14],采用3 步3 阶的显式辛算法,即SFDTD(3,4)方法数值求解含时薛定谔方程,其实部和虚部波函数的迭代公式可离散成如下形式:
其中cl,dl为辛传播因子[14];n表示时间步,m代表单个时间迭代中子迭代步数,l表示在m个子迭代步数中的第l步计算,i,j,k表示坐标.
2.2 SFDTD(3,4)方法稳定性条件的扩展
不失一般性,假定V(r)=0,等式(3)的空间四阶差分形式可以写成如下形式:
这里kx,ky,kz表示相应方向的波数.
对(12)式进行3 阶时间辛积分近似处理,则其系统时间演化矩阵的离散形式S为
由于离散矩阵是行列式值为1 的辛矩阵,矩阵特征值λ 对应的特征方程可以写为
(15)式的解为
稳定性条件要求|λ1,2|=1,矩阵S的迹满足如下条件:
将(14)式依次相乘,得到
其中gl的值可以通过辛传播因子cl和dl来计算,m是单个时间迭代中子迭代步数.
将其代入(17)式和(18)式,则关于时间步长Δt的不等式需满足如下形式:
为确保数值稳定性,时间步长Δt应小于(21)式右边函数的最小值,令函数Q中sin2(ku∆u)=0(u=x,y,z),可得传统SFDTD(3,4)算法的CFL 稳定性条件:
(22)式是确保SFDTD(3,4)方法中所有空间频域场分量保持稳定,然而根据文献[16,17],只有空间频域中一部分的低频分量对计算结果有影响,而剩余部分的高频分量的幅值较小,同时对数值计算结果的正确性影响几乎为零.然而,若采用较大的时间步长,会导致空间频域中高频分量的幅值呈现指数增加,并导致计算结果发散.基于此,将SFDTD(3,4)方法中空间频域场分量限制在一个范围,即在(21)式中,将波函数限制在一个以kmax为半径的球形区域内:
然后将(23)式代入(20)式得
其中q=kmax∆/2,则关于时间步长的不等式可写成如下形式:
根据(25)式,时间步长Δt与函数Q中的θ 和φ有关,Q(θ,φ) 随θ,φ的变化如图1 所示,通过数值求解得到函数Q(θ,φ) 在θ=0.304π,φ=0.25π 取得最大值.将θ=0.304π,φ=0.25π 代入(20)式得到Qmax(0.304π,0.25π),然后根据(21)式得到关于时间步长的不等式为
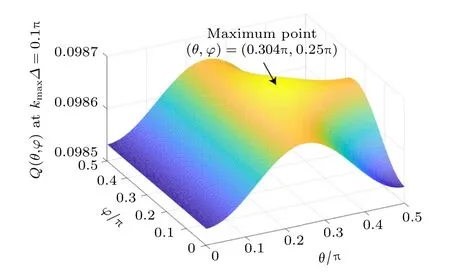
图1 kmax ∆ =0.1π 时,Q(θ,φ )随θ,φ 的变化Fig.1.Variation of Q(θ,φ) with θ,φ at kmax ∆ =0.1π.
其中ΔtCFL是传统SFDTD(3,4)方法求解薛定谔方程的最大离散时间步长;CE 表示传统SFDTD(3,4)算法的CFL 条件被扩展的倍数.图2 是关于CE 的数值变化曲线,可以发现CE 大于1.这表明通过滤除SFDTD(3,4)方法中空间频域场分量中的高频分量,可以使得传统SFDTD(3,4)方法的CFL 得到进一步扩展.
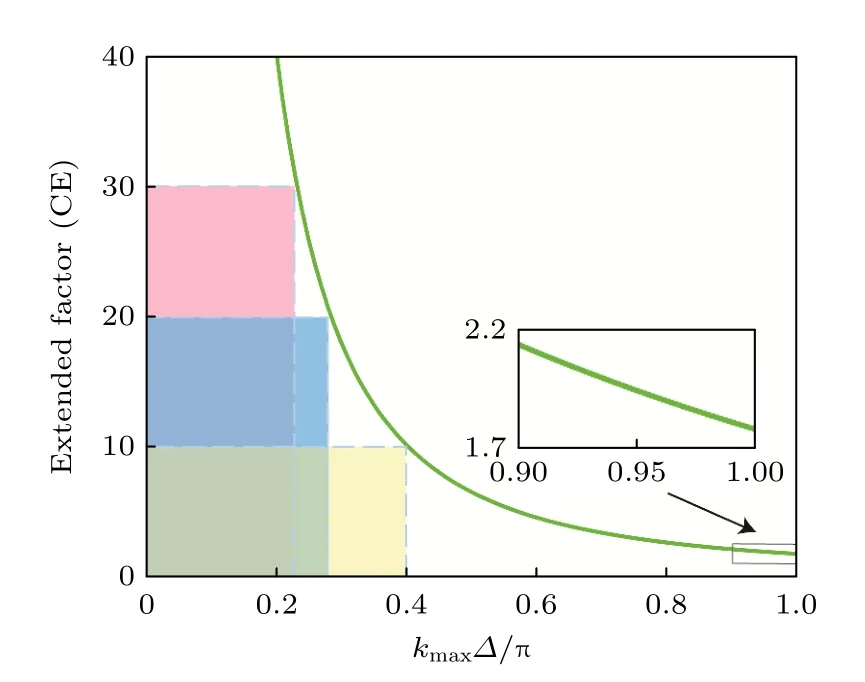
图2 扩展因子CE 随kmax ∆ 的变化Fig.2.Value of CE varying with kmax ∆ .
当CE 的值确定后,根据(24)式和(27)式可以得到kmax∆的值,然后定义低通滤波器半径R,其计算公式为
图3 为采用不同CE (CE1
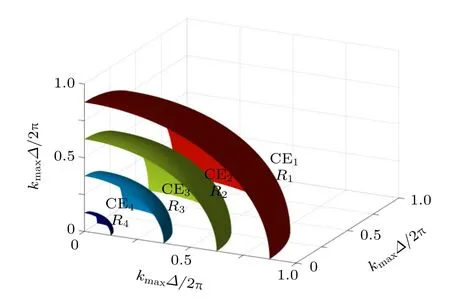
图3 不同CE 的值所确定的滤波半径Fig.3.Filter radius determined by different values of CE.
3 色散分析
根据文献[14],SFDTD(3,4)方法求解薛定谔方程的数值色散方程为
另外,薛定谔方程的解析色散关系式为[19]
定义数值色散误差 Errω:
令∆=A/kmax,每个波长的网格数由2π/A给出.同时将(26)式,(29)式和(30)式代入(31)式得
图4(a),(b)分别为FDTD 方法和SFDTD 方法在CE=1 情况下的数值色散误差.这里需要说明的,SF-SFDTD 方法在CE=1 情况下的色散误差与SFDTD 方法的色散误差是相同的.这是因为SF-SFDTD 方法与SFDTD 方法采用相同的数中额外加入滤波操作过程.若CE=1,此时时间步长满足时间稳定性条件,则不需要采用滤波操作,则SF-SFDTD 方法与SFDTD 方法具有相同的计算过程,两种方法所具有的数值色散误差也是相同的.
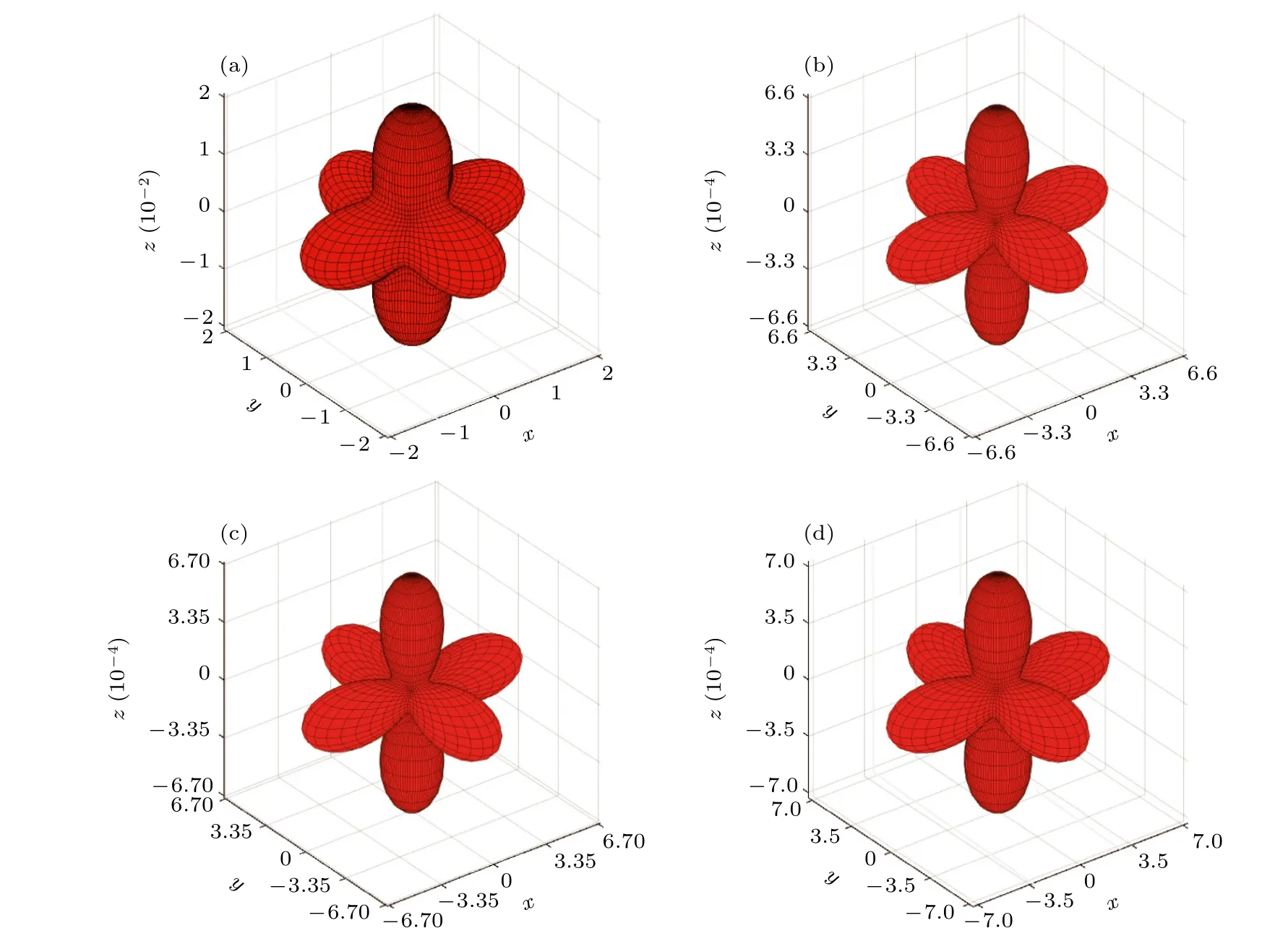
图4 FDTD(2,2),SFDTD(3,4)和SF-SFDTD(3,4)方法的数值色散误差 (a) FDTD(2,2)(CE=1);(b) SFDTD(3,4)(CE=1);(c) SF-SFDTD(3,4)(CE=5);(d) SF-SFDTD(3,4)(CE=10)Fig.4.Curves of numerical dispersion error for the FDTD(2,2),SFDTD(3,4) and SF-SFDTD(3,4) method: (a) FDTD(2,2)(CE=1);(b) SFDTD(3,4)(CE=1);(c) SF-SFDTD(3,4)(CE=5);(d) SF-SFDTD(3,4)(CE=10).
为了进一步比较三种方法的数值色散误差,图4(c),(d)给出了SF-SFDTD 方法在CE=5 和CE=10 情况下的数值色散误差.可以发现,SFSFDTD 方法的数值色散误差略大于SFDTD 方法的数值色散误差,这是因为随着时间步长的增加,时间域上的采样分辨率下降,导致数值色散误差增加.但需要说明的是,随着时间步长的增加,SFSFDTD(3,4)方法的数值色散误差增加不明显,与传统方法的数值色散误差处于同一量级.值得注意的是: 即使在CE=10 的情况下,SF-SFDTD(3,4)方法相较于FDTD(2,2)方法仍具有较低的数值色散误差.这表明在SF-SFDTD(3,4)方法中采用较大的时间步长求解含时薛定谔方程,仍能得到十分准确的数值结果.
4 数值计算
为了验证本文所提SF-SFDTD(3,4)方法的正确性和有效性,通过数值求解二维和三维薛定谔方程,计算量子阱结构的本征态和特征频率,并将计算结果与其他方法所得计算结果进行对比.
4.1 二维量子阱
二维量子阱模型的尺寸为Lx=Ly=2.9 mm,空间步长Δx=Δy=0.1 mm,采用镜像原理构建边界条件[20],边界条件ψ(0,y)=ψ(Lx,y)=ψ(x,0)=ψ(x,Ly)=0,系统的势能V(r)=0.
图5 和图6 分别给出了传统SFDTD(3,4)方法(CE=1)和SF-SFDTD(3,4)方法(CE=2,4,5)计算所得二维量子阱结构的特征频率和本征态ψ2,2.数值结果表明,SF-SFDTD(3,4)方法采用不同的时间步长(CE=2,4,5)计算所得结果与传统SFDTD(3,4)方法(CE=1)计算所得结果一致.另外,图5 还给出了FDTD(2,2)方法的计算结果,结果表明SF-SFDTD(3,4)方法相较于FDTD(2,2)方法具有更高的数值计算精度.对比以上不同方法的计算结果,进一步验证了本文所提SFSFDTD(3,4)方法的正确性.
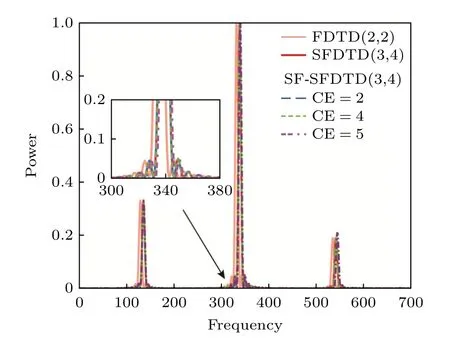
图5 二维薛定谔方程的特征频率Fig.5.Eigenfrequencies of the two-dimensional Schrödinger equation.
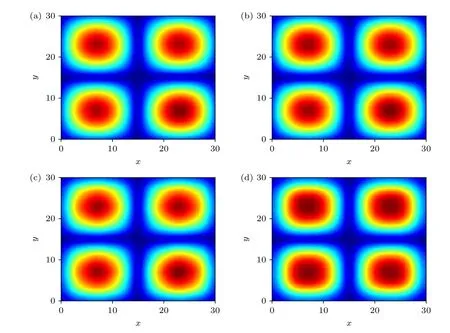
图6 二维薛定谔方程在不同时间步长下的本征态(ψ2,2) (a) CE=1;(b) CE=2;(c) CE=4;(d) CE=5Fig.6.Eigenstates of two-dimensional Schrödinger equation at different time steps (ψ2,2): (a) CE=1;(b) CE=2;(c) CE=4;(d) CE=5.
表1 对比了SFDTD(3,4)方法和SF-SFDTD(3,4)方法的数值计算效率.由表1 可以看出,当CE=5 时,SF-SFDTD(3,4)方法的仿真时间小于传统SFDTD(3,4)方法的仿真时间,这表明在取较大的时间步长情况下,SF-SFDTD(3,4)方法在计算效率方面相较于SFDTD(3,4)方法更具有优势.的6 倍时,SF-SFDTD(3,4)方法和SFDTD(3,4)方法的数值计算结果仍较为一致,同时可以发现FDTD(2,2)方法的计算结果偏离其他两种方法的计算结果,再一次验证了本文所提方法的正确性.
为了定量分析FDTD(2,2)方法、SFDTD(3,4)方法和SF-SFDTD(3,4)方法计算特征频率结果的相对误差,定义相对计算误差:
4.2 三维量子阱
三维量子阱模型的尺寸为Lx=Ly=Lz=3 mm,空间步长Δx=Δy=Δz=0.1 mm,边界条件ψ(0,y,z)=ψ(Lx,y,z)=ψ(x,0,z)=ψ(x,Ly,z)=ψ(x,y,0)=ψ(x,y,Lz)=0,其势能V(r)=0.
图7 和图8 分别给出了FDTD(2,2)方法(CE =1),SFDTD(3,4)方 法(CE =1)和SFSFDTD(3,4)方法(CE=2,4,6)计算所得三维量子阱结构的特征频率和本征态ψ2,2,2.由图7 和图8 可知,当SF-SFDTD(3,4)方法所采用的时间步长是传统SFDTD(3,4)方法最大离散时间步长

图7 三维薛定谔方程的特征频率Fig.7.Eigenfrequencies of the three-dimensional Schrödinger equation.

图8 三维薛定谔方程在不同时间步下的本征态(ψ2,2,2) (a) CE=1;(b) CE=2;(c) CE=4;(d) CE=6Fig.8.Eigenstates of three -dimensional Schrödinger equation at different time steps (ψ2,2,2): (a) CE=1;(b) CE=2;(c) CE=4;(d) CE=6.
其中G(f) 和Ganalysis(f) 分别表示三种方法计算所得特征频率结果和解析结果.如图9 所示,虽然SF-SFDTD(3,4)方法在CE=2,4,6 情况下,其相对计算误差大于SFDTD(3,4)方法(CE=1)的相对计算误差,但保持在较低的误差水平.另外,即使CE=6,SF-SFDTD(3,4)方法的相对计算误差仍小于FDTD(2,2)方法的相对计算误差.
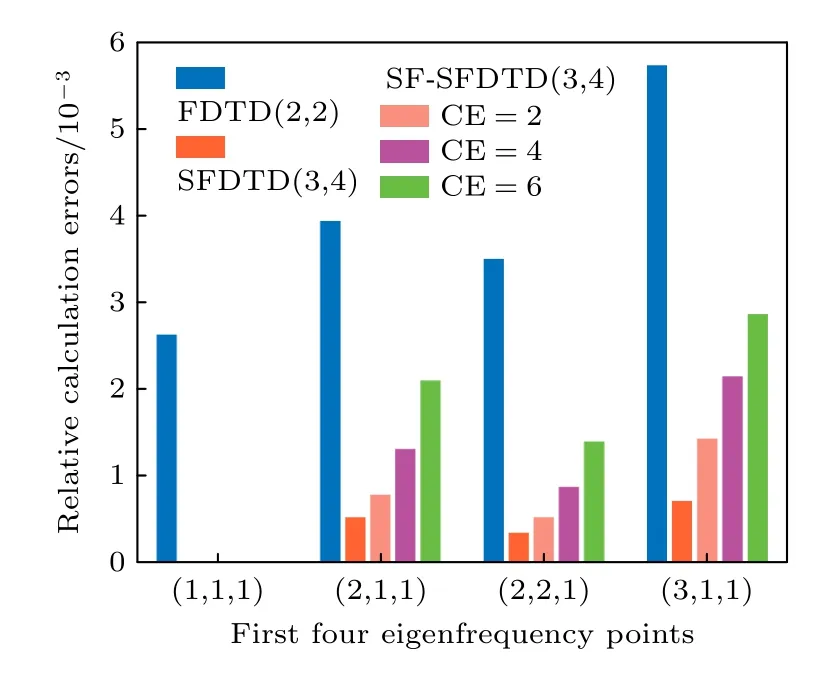
图9 FDTD(2,2),SFDTD(3,4)和SF-SFDTD(3,4)方法计算所得前四个特征频率点的相对计算误差Fig.9.Relative calculation errors of the first four characteristic frequency points were calculated by FDTD(2,2),SFDTD(3,4) and SF-SFDTD(3,4) methods.
表2 列出了SFDTD(3,4)方法和SF-SFDTD(3,4)方法取不同时间步长下的仿真时间.由表2可以看出,当CE=6 时,SF-SFDTD(3,4)方法的仿真时间小于传统SFDTD(3,4)方法的仿真时间,这表明在三维仿真环境下,SF-SFDTD(3,4)方法在取较大的时间步长情况下相较于SFDTD(3,4)方法更具有计算优势.

表2 SFDTD(3,4)和SF-SFDTD(3,4)方法数值求解三维薛定谔方程的运行时间的运行时间Table 2. Execution time(s) for SFDTD(3,4) and SF-SFDTD(3,4) methods for solving three-dimensional Schrödinger equation.
5 结论
本文提出了一种新的高稳定性SF-SFDTD(3,4)方法用于数值计算含时薛定方程.相较于隐式无条件稳定的时域数值计算方法,SF-SFDTD(3,4)方法不改变传统SFDTD(3,4)方法的迭代公式,只需要在每一次的数值计算过程中加入空间滤波操作,滤除因采用不满足CFL 稳定性条件的时间步长而产生的空间高频分量.因此,该方法与传统SFDTD(3,4)方法具有较高的兼容性,数值实现较为容易.另外,文中给出了SF-SFDTD(3,4)方法的数值稳定性和色散误差分析,并通过数值算例验证了该方法的正确性和有效性.总的来说,本文所做工作为含时薛定谔方程的求解提供了一种高效的数值求解器,也拓展了时域数值方法在量子计算领域的应用范围.未来可以将本文所提SFSFDTD(3,4)方法用于数值求解复杂的麦克斯韦-薛定谔耦合方程,解决半经典理论框架下的量子-电磁问题.
