Classifying rockburst with confidence: A novel conformal prediction approach

Bemah Ibrahim,Isaac Ahenkorah

University of South Australia,UniSA STEM,SA 5000,Australia

Keywords:Rockburst Machine learning Uncertainty quantification Conformal prediction

ABSTRACT The scientific community recognizes the seriousness of rockbursts and the need for effective mitigation measures.The literature reports various successful applications of machine learning (ML) models for rockburst assessment;however,a significant question remains unanswered:How reliable are these models,and at what confidence level are classifications made? Typically,ML models output single rockburst grade even in the face of intricate and out-of-distribution samples,without any associated confidence value.Given the susceptibility of ML models to errors,it becomes imperative to quantify their uncertainty to prevent consequential failures.To address this issue,we propose a conformal prediction (CP) framework built on traditional ML models (extreme gradient boosting and random forest) to generate valid classifications of rockburst while producing a measure of confidence for its output.The proposed framework guarantees marginal coverage and,in most cases,conditional coverage on the test dataset.The CP was evaluated on a rockburst case in the Sanshandao Gold Mine in China,where it achieved high coverage and efficiency at applicable confidence levels.Significantly,the CP identified several‘‘confident”classifications from the traditional ML model as unreliable,necessitating expert verification for informed decision-making.The proposed framework improves the reliability and accuracy of rockburst assessments,with the potential to bolster user confidence.

1.Introduction

For several decades,rockburst has been a hazardous instability phenomenon of rock masses in underground mining projects that continues to be a cause for concern.It occurs when accumulated strain energy in rocks is suddenly and forcefully released [1,2],causing severe damage to mining equipment,infrastructure,and even endangering workers’lives.Numerous recorded cases worldwide [3,4] serve as examples of its destructive potential.

Rockburst is influenced by various factors,including the mechanical properties of rocks,geological structure,excavation methods,and the in-situ stress[5].Following underground excavation,the redistribution of in-situ stress results in rock instability[6,7].In high-stress environments,the failure process is primarily controlled by stress-induced fractures around the excavation zone,while in low-stress environments,the distribution and continuity of natural fractures play a significant role in governing the failure process [8].Rockburst phenomenon remains a huge challenge for the utilisation of deep underground space [5].It is likened to cancer in the medical field[9],underscoring its seriousness,complexity,and the challenge of finding effective solutions.With underground activities progressing to deeper depths,rockbursts are expected to become more prevalent [2].Therefore,developing classification models for evaluating rockburst intensity is critical for the design of safe and sustainable mining projects [10,11].

The development of classification models for rockburst has been widely studied [11,12].Since the pioneering study by Cook et al.[1],numerous models have emerged over the past decade,including empirical [13,14] and numerical [14,15] models,aimed at either classifying rockbursts or predicting their potential [16].Recently,intelligent techniques,particularly machine learning(ML)models like support vector machines(SVM)and artificial neural network (ANN) have been successfully used to classify rockburst occurrences [5,16,17].The widespread adoption of ML is largely attributed to their ability to accommodate many influential parameters and accurately identify complex nonlinear patterns in rockburst data that are otherwise not readily apparent [16].Typically,a ML model is trained using a dataset where the target variable,such as rockburst grade,is known and related to a set of covariates.The model is trained to identify patterns and relationships between the covariates and the target variable in the training data.Once the model is trained,it can be used to classify the rockburst grade for new data based on the values of the covariates.

Several authors have used either standalone ML models[18,19]or combined two or more models in a hybrid approach[20–22].For instance,Zhao et al.[23] used decision trees (DT) to classify rockburst using microseismic monitoring data.Ghasemi et al.[24]similarly employed DT for evaluating rockburst intensity with an accuracy of 90.23%.Xue et al.[10] hybridised a particle swarm optimization(PSO)and extreme learning machine(ELM)to classify rockburst in several underground projects with an accuracy of 98%.Shukla et al.[25] used extreme gradient boosting (XGB),DT,and SVM to classify the occurrence of rockburst in various underground projects,achieving an accuracy of more than 88% with all models.Other recent studies [26–28] have also demonstrated the applicability ML in rockburst classification or prediction.

One of the primary challenges posed by ML models lies in the determination of the reliability of their classifications,particularly when applied to new datasets[29].This challenge becomes particularly pronounced with out-of-distribution samples,where classifications may become arbitrary guesses [30].In the case of rockburst,a phenomenon characterized by dynamic complexity,there are instances where the true grade is inherently ambiguous and difficult to determine.However,traditional classifiers are compelled to provide a single rockburst grade,often leading to erroneous results [31],without any associated confidence value.In high-risk tasks such as rockburst assessment,where incorrect outcomes can have catastrophic consequences,it is crucial to quantify the uncertainty associated with the classifications made by ML models.Therefore,it becomes imperative to incorporate measures of confidence that can identify cases where the model’s classification may be unreliable or uncertain.This allows a human operator to intervene,provide additional information,or make the final decision based on the identified uncertainty.

Conformal prediction (CP) framework [32] has been proposed for addressing the uncertainty quantification of predictive models.Unlike existing models that output a single class for a given instance,CP generates a statistically rigorous uncertainty set of classes [33],which provides guarantee for the classification error[32,34],provided the rockburst data are exchangeable[32],a property very crucial for developing and deploying reliable artificial intelligence systems in rockburst assessment.CP makes no assumption about the data distribution [30] and can be applied to any ML classifier [35,36] to assess its robustness and predictive power [37].The desirable properties of CP have led to its wide application in critical areas of medicine such as in drug discovery[29,38],tumour segmentation studies[33]and estimating diagnostic uncertainty [39,40].Despite the popularity of ML models in classifying rockburst potential,the use of the CP framework to provide reliable estimations in this field is currently limited.As a result,there is a need to develop CP frameworks that can offer valid classifications.This study aims to develop a CP framework for rockburst assessment and some of the major significant contributions are listed as follows:

(1) introducing a novel CP framework that classifies rockburst intensity and effectively communicating the associated uncertainty to stakeholders,

(2) demonstrating how CP can be used to detect unreliable classification of rockburst grade,and

(3) presenting a more informative approach for assessing and comparing ML model for rockburst classification.

Section 2 presents data acquisition.In Section 3,the proposed method including the rationale behind the CP in the context of classification and the model building process is presented.The empirical outcomes are discussed in Section 4,where two CP models are extensively evaluated and compared.Finally,the key findings of the study are summarized in Section 5.

2.Data acquisition

The selection of covariates in this study was based on previous research [41,42],which classified rockburst using parameters representing the rockmass strength,geological structures,geo-stress conditions,excavation methods and sizes.The study utilized a database of 314 real rockburst cases from various sources(Table 1)consisting of six influential covariates such as the maximum tangential stress (σθ),uniaxial compressive strength (σc),tensile strength (σt),stress ratio (σθ/σc),brittleness ratio (σc/σt),and strain energy storage index (wet).The σθreflects the strata stress character of rockburst and is calculated according to the stress of the surrounding rock.σcand σtrepresent the geological strength of the rockmass and are obtained from uniaxial compression test and Brazilian splitting tensile test respectively.σθ/σcrepresents the stress coefficient;which induces rockburst when the value is greater than or equal toKs(Lu Jiayou criterion),and this value is also dependent on the σc/σt[43].The higher the σc/σtratio is,the more brittle the rock is and the more frequent rockbursts occur[44].Thewetis a rock property that reflects the proportion of strain energy retained compared to that dissipated during a single loading-unloading cycle of uniaxial compression[45].wetis determined through rock loading and unloading test.These representative variables,as utilized by previous researchers [10,21,42] were used as input variables to classify rockburst grade.The rockburst level was categorized into four distinct groups: none (50 cases),light (96 cases),moderate (115 cases),and strong (53 cases)(Table 1),using standard classification criteria outlined in Table 2.

Table 1 Source of rockburst cases compiled by Li et al.[46].

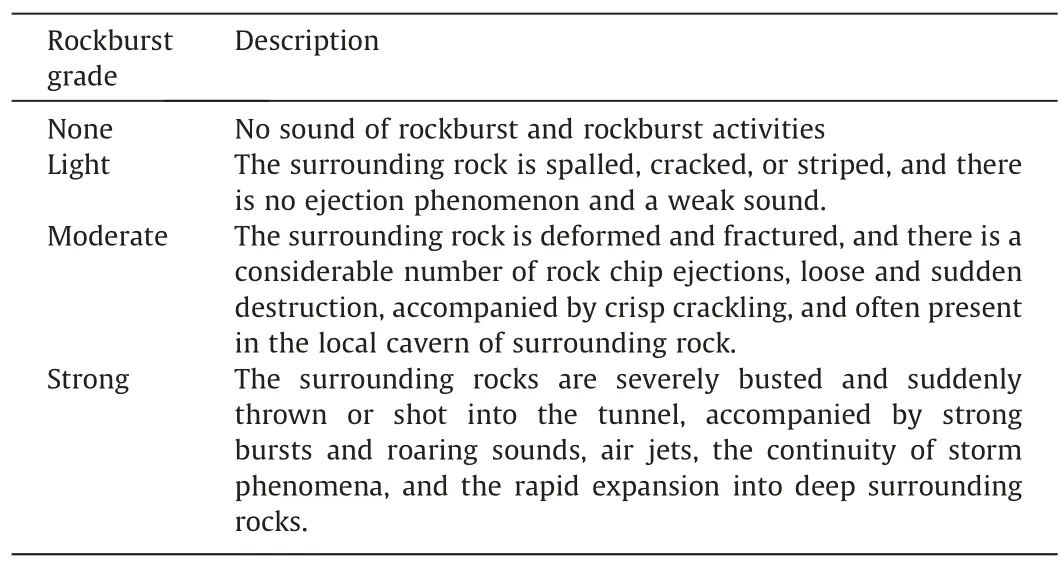
Table 2 Classification of rockburst grade [42].

Table 3 presents the statistical distribution of the covariates.To address the differences in data sources,the dataset was standardize using Eq.(1) to mitigate any potential variations between the sources.

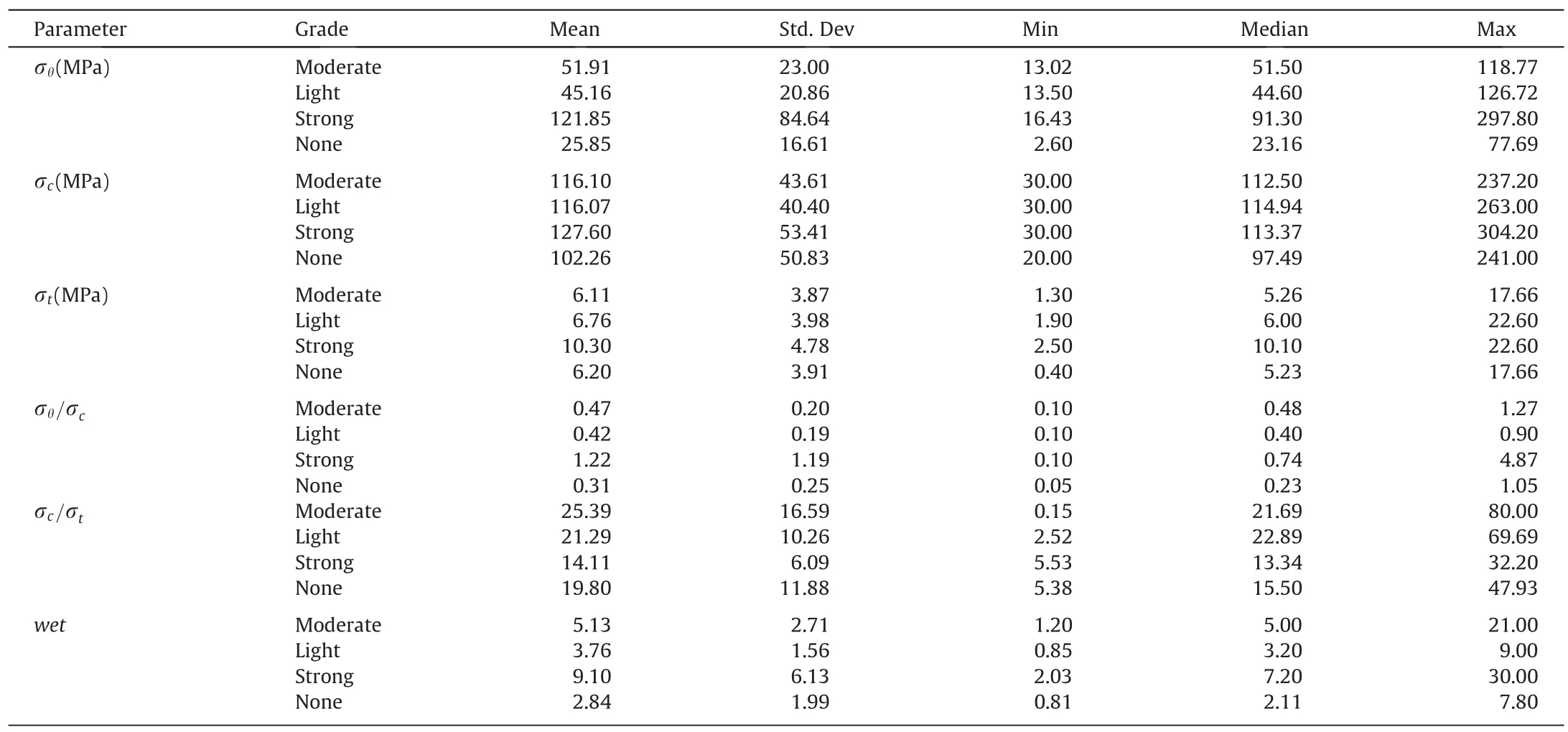
Table 3 Statistical description of the utilised database.

Fig.1 presents a pair plot of the covariates in the rockburst dataset.This plot allows for a visual examination of the relationships between each pair of covariates,while also displaying the univariate distributions of each covariate along the diagonal.The points in the plot are colour-coded based on the corresponding rockburst grade.Upon analysing the figure,it becomes evident that the different rockburst grades do not exhibit clear linear separability using any two covariates.Instead,they overlap with each other,indicating a complex relationship between the covariates and the rockburst grades.However,notable patterns emerge from the plot.Specifically,it is observed that high values of σθ(＞192 MPa) are associated with strong rockburst grade.Similarly,samples with σθ/σcvalues exceeding 1.7 are linked to strong rockburst grade.

Fig.1.Distribution of the input variables graded according to rockburst intensity.

3.Proposed method

3.1. Intuition on conformal predictions

The CP framework offers uncertainty quantification of rockburst assessment by ensuring that classification errors are bounded by a user-defined confidence level [32,53].This approach is proven to provide rigorous classification sets that are valid in a distribution-free sense [33,54–56],which is particularly useful in classification tasks such as the one explored in this study.The CP approach used in the study intuitively involves the following steps:

(1) Firstly,the data is split into training,calibration,and testing sets.

(2) Next,a machine learning model is trained on the training set.

(3) Then,a non-conformity measure is chosen,and the nonconformity scores are computed for the calibration data.

(4) The confidence level is specified,and the quantile is computed.

(5) The CP approach is applied to the testing data or external set instances,where the non-conformity of each instance is evaluated with respect to the training data.

(6) All labels that produce a score higher than the quantile are selected to form the classification set.The reliable classifications are identified based on user-defined significance and confidence levels.

(7) Finally,the validity and efficiency of the generated CP are evaluated.

Consider a rockburst training dataTwithninstances,（X，Y）=（xi，yi），···，（xn，yn）where samples were drawn exchangeably from an unknown distribution PX/Y.As depicted in Fig.2,in a traditional classification task,ML is trained to predict a single classyi,for each rockburst instancexiwhen presented with new data of an unknown target.

Fig.2.Illustration of classification output of CP and traditional ML classifiers (image of observed sample taken from Xiao et al.[57]).

However,the CP framework takes a different approach.Instead of outputting a single class,it constructs a classification set ´Cn，α（Xn+1）,at a given risk level α,for a new observation(Xn+1，Yn+1).This classification set guarantees marginal coverage in Eq.(2)[58],such as follows [37]:

The inductive CP framework adopted in this study randomly splitTinto two:proper trainingTt⊆Tof sizeL＞Mand calibration dataTc⊆Tof sizeM-L.The base ML model is then trained onTt.Then,the trained model is used to predict the rockburst grade of the instances inTt.The predicted outcome and their true grade are used to compute the non-conformity scores,si[30].siserves to quantify the non-conformity (or ‘‘strangeness”) of a new instance with respect to those in theTt.Several methods,such as the least ambiguous with bounded error levels (LABEL) [59]and adaptive prediction set (APS) [58] have been proposed for computing thesi.In this study,the LABEL method was adopted.When using the LABEL method,the conformity score is defined as one minus the probability output of the true label.Eq.(3)is then used to calculate the conformity score for each pointiinTc:

wheref（xi）［yi］is the probability output of the model for the true class;the quantileqˆis estimated by finding the non-conformity scores that are smaller than 1-α,as shown in Eq.(4):

To construct the prediction set for an unobserved response of a feature vector,CP leverages previous identically distributed and exchangeable observations of covariates and rockburst grade inT[60].Newsiare computed for each sample in the new dataset.The rockburst labels with highersithan the estimatedare then output as the classification set,as shown in Eq.(5):

The LABEL method is simple and provides a theoretical guarantee on the marginal coverage in Eq.(6)[30].That is,the probability that the true label belongs to the classification set is between 1-α and 1

Eq.(7) represents the conditional coverage property,which aims to return classification sets with 1-α coverage for every input value in the testing data.However,this property cannot always be ensured.Additionally,when using the LABEL method,uncertain samples may result in empty classification sets and the generated classification sets may be smaller in size.

More details on the LABEL method are provided in Sadinle et al.[59].

3.2. Model building process

The step-by-step account of the study process is illustrated in Fig.3.As mentioned earlier,the study utilized a dataset consisting of 314 instances of rockburst,which were obtained from previous research.The dataset was divided into three parts,namely,the training data(70%),the calibration data(15%),and the testing data(15%),using a stratified approach to ensure that the rockburst grades were distributed proportionally[61].The percentage distribution of the grades in each set is provided in Table 4.To address the differences in data sources,the covariates were standardized using Eq.(8) to mitigate any potential variations between the sources.

Fig.3.Workflow of the proposed CP framework.

Table 4 Distribution of the various rockburst classes in the complete,training calibration and testing data.

The training data was utilised to construct the underlying XGB and RF model for the CP as well as two other ML models namely:SVM and DT for comparison purposes.The calibration data was used to calibrate the conformity scores utilizing the MAPIE(Model Agnostic Prediction Interval Estimator) library developed by Taquet et al.[37].To prevent overfitting,the training data was not used for calibration [30,37].The initialization of MAPIE requires two main parameters: thecv and method.Thecv parameter specifies the splitting strategy for training the model and calibrating the conformity scores.In this study,the prefit option was used,as the base XGB model was already trained on the training data.The method parameter controls the strategy for constructing the classification sets.As earlier indicated,the LABEL method was used [59] by specifying the method parameter as score.

MAPIE is initialised by specifying the base model.Two base models namely XGB and RF were evaluated in this study.Consequently,in the subsequent part of this discussion,XGB-CP and RF-CP denote the resultant CP models for XGB and RF,respectively.Once initialised,the CP was fitted to the calibration data.The CP was used to classify the unseen test data by specifying the confidence level.Finally,the two CP models were evaluated using the marginal coverage,conditional coverage,efficiency,and size of average classification sets at confidence levels of 97%,95%,90%,and 80%.It is important to note that the study involved a multiclass classification task,hence,three possible outcomes are anticipated:

(1) Single prediction

(2) Multiple prediction

(3) Empty set (no class assignment)

The latter two outcomes denote situations in which conformal prediction exhibits uncertainty at the designated confidence level.Multiple prediction implies that the rock sample shares similarities with multiple grades,making it unreliable to predict as a single grade.Conversely,predicting an ‘‘empty set” implies the sample is dissimilar to either grade at the specified confidence level.

4.Results and discussion

4.1. Evaluation of traditional classifiers

The CP models developed use XGB and RF as their underlying model,so it is necessary to compare their performance against other state-of-the-art ML models.The test dataset is used to evaluate the performance using overall accuracy calculated using Eq.(9).

where TP,TN,FP,and FN are true positive,true negative,false positive,and false negative respectively.Based on the evaluation results presented in Table 5,the XGB and RF demonstrated superior generalization ability compared to SVM and DT.XGB and RF achieved equal testing accuracy of 0.83.However,XGB overfits the training data as similarly reported in Li et al.[46],who utilized the same database.

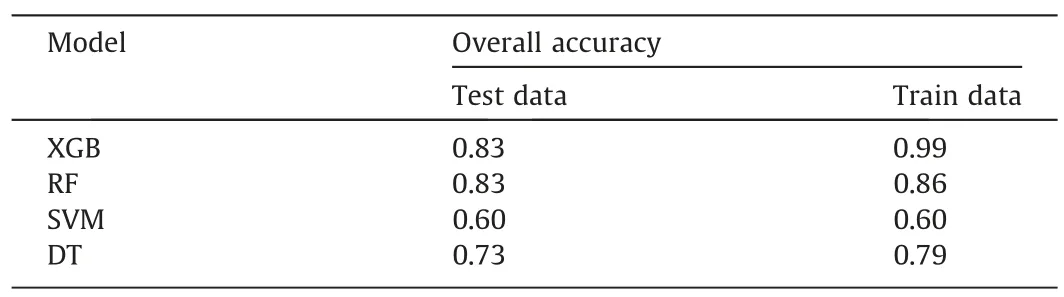
Table 5 Accuracy performance report of developed ML models.

However,the accuracy metric tends to be biased toward the majority class in imbalanced datasets [62] such as the current database.Therefore,single-class metrics,namely precision,sensitivity,andF1 measures,were additionally utilized to evaluate the performance of classifiers.These metrics are calculated for each individual class and are less affected by class imbalance,making them more suitable for assessing classifiers in domains characterized by skewed data distributions [62].Precision (defined in Eq.(10))measures the correctly classified positive class samples.Sensitivity computed using Eq.(11),measures the percentage of the relevant materials data sets that were correctly identified.

TheF1[63]measures the balance between precision and sensitivity and is computed using Eq.(12) as:

The class-wise performance of the ML models is presented in Table 6.For easy comprehension,the results are compared in Figs.4,5 and 6 for precision,sensitivity andF1 score respectively.

Table 6 Single class performance report of developed ML models.

Ultimately,models with high sensitivity are desired especially for strong rockburst grades.

High sensitivity for strong rockburst grade means that,the rate of predicting strong grade as other grades is low,which serves as a safety buffer for preventing consequential failures.From Fig.4,all the ML models generally achieve more than 0.70 sensitivity with RF obtaining the highest score of 1.

Fig.4.Sensitivity performance of the ML models.Notes: N: None;L: Light;M: Medium;and S: Strong.

Beyond sensitivity,the model shouldn’t not be predicting every sample as strong grade when they are not.With this high precision is sought for.According to the precision results shown in Fig.5,all the models except DT obtained a precision score of more than 0.85.

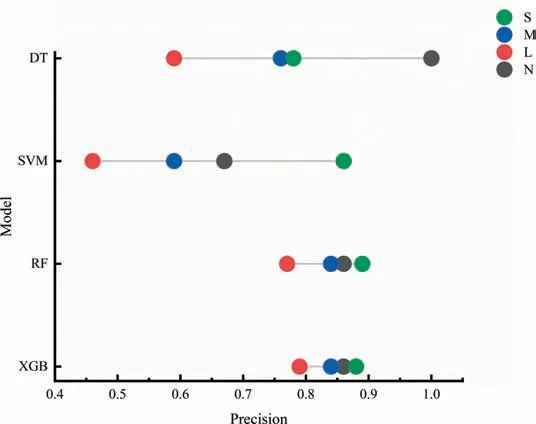
Fig.5.Precision performance of the ML models.Note: N: None;L: Light;M: Medium;S: Strong.

On the balance side(Fig.6),RF obtained the highestF1 score of 0.94 for the strong rockburst grade and 0.86 for the medium grade.Generally,the ensembles (RF and XGB) markedly outperform the DT and SVM for all rockburst grades.

Fig.6.F1 score performance for the ML models.Note: N: None;L: Light;M: Medium;and S: Strong.

An essential objective in rockburst risk assessment is to accurately identify the potential for strong rockbursts occurrence.From the confusion matrix in Fig.7,the XGB and RF models,having low false negative rates(i.e.,incorrectly classifying a rockburst grade as other grade) for the strong and medium rockburst grade is preferred.Thus,the XGB and RF model were selected to build the CP.

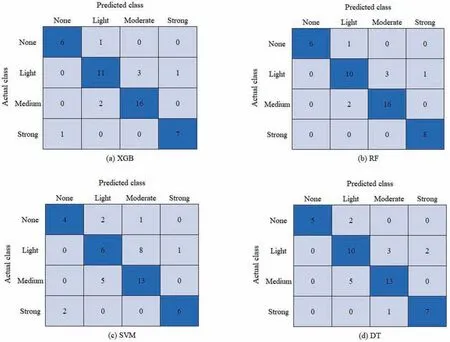
Fig.7.Confusion matrix for the ML models.

4.2. Conformal prediction

4.2.1.Marginalanalysis

Fig.8a and b show the marginal coverage and average classification set for the XGB-CP and RF-CP,respectively.The results of the marginal analysis are presented in Table 7.For a model to be considered valid,the error rate cannot exceed the prespecified significance level of the conformal predictor [40].In essence,for a confidence level,such as 95%,the prediction sets should contain the true rockburst grade in a minimum of 95% of instances for the model to be considered valid.From Fig.8a,both models achieve higher or close-to-target marginal coverage with the RFCP achieving relatively higher coverage than XGB-CP (Fig.8a).Overall,it is confirmed that CP guarantee marginal coverage independent of the ML model used [58,64].Beyond coverage,models must also be informative,avoiding prediction sets that contain multiple rockburst grades.Therefore,models with smaller average prediction set sizes are desirable.Fig.8b shows an increasing size of the classification set with an increasing confidence level for both methods.Generally,RF-CP produces a smaller classification set compared to the XGB-CP.

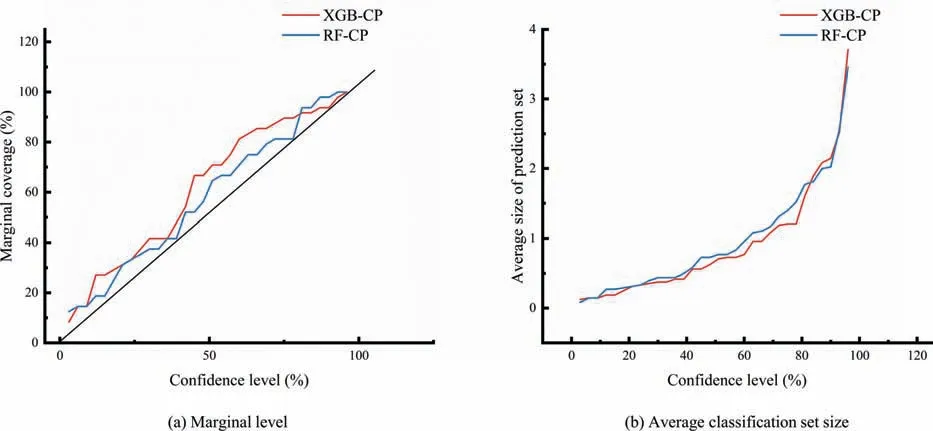
Fig.8.Graph of the marginal coverage and average classification set size as a function of confidence level.

Table 7 Marginal coverage and average set size for four specific confidence level.

The study further analysed the impact of confidence level on the performance of CP,specifically examining the outputs for the 97%,95%,90%,and 80%confidence levels.According to Table 7,the two CP models guarantee marginal coverage for all the confidence levels.The average size of the classification set for RF-CP is generally lower compared to XGB-CP.

4.2.2.Class-wiseconditionalanalysis

Given the complexities that may be associated with classifying each grade,the class-wise performance must be explored toascertain the adaptiveness (formalised in Eq.(6)) of the CP models.Table 8 presents the results.As previously noted,practitioners are particularly interested in how well these models perform on individual classes,especially the strong grade.It is evident from the table that the models provide a class-wise coverage guarantee,except for three cases (italicised).The guarantee for conditional coverage does not hold for various rockburst grades.As noted in previous studies,it is impossible to guarantee class-wise coverage[30,32,65,66].

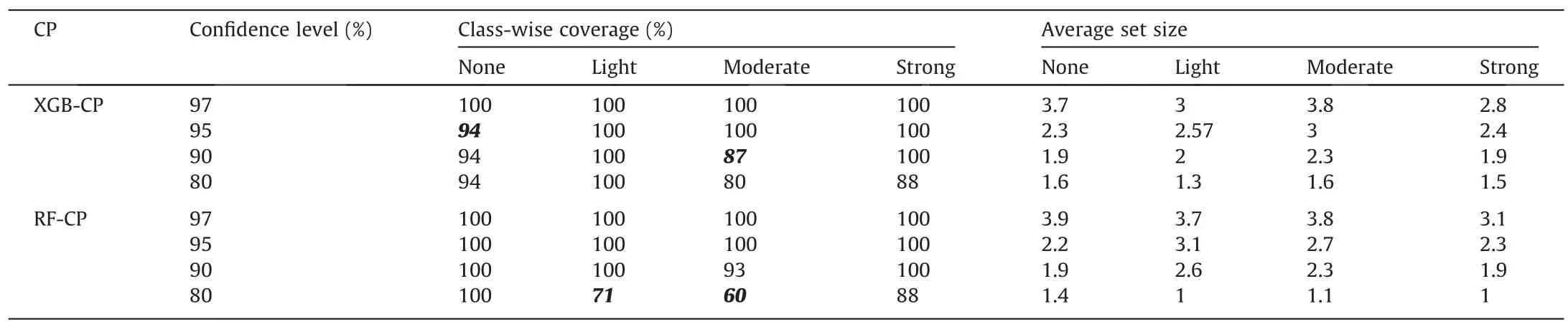
Table 8 Class-wise performance of the developed CP.

According to Fig.9,the RF-CP generally provides better or equal class-wise coverage across all confidence levels except for light and moderate grades at a confidence level of 80%.In terms of average set size,XGB-CP produces a relatively smaller set size at 97%confidence level and a larger set size at 80%level compared to RF-CP.Generally,the average set size for the various rockburst grades increases as the confidence level increases.

Fig.9.Comparison of conditional coverage (left) and classification set size (right) for the various rockburst grade.

4.2.3.Analysisofsingleormultipleclassificationsandefficiency

The classification outputs of the CP models are classified into four categories: (1) sets with one label,(2) sets with two labels,(3) sets with three labels,and (4) sets with all labels.Table 9 contains the specifics of these categories.The focus is on the number of outputs that fall into the last three categories,as the goal is to minimize this number.These outputs indicate instances where the CP is uncertain in only one label at the required confidence level,which is of primary importance.

Table 9 Percentage of test data classified as single or multiple classes.

The results are presented in Fig.10 using bar charts to aid comprehension.The chart shows a decreasing percentage of singlegrade classification as the confidence level increases.At a confidence level of 97%,none of the rockburst instances was classified as one label.At a confidence level of 95%,XGB-CP classified 10%of the test data as one label,while RF-CP classified 6%.Generally,XGB-CP had a higher classification rate for one label at higher confidence levels (＞80%)compared to RF-CP.However,at an 80% confidence level,RF-CP classified 63% as one label,whereas XGB-CP classified 54%.It should be noted that RF-CP also classified 8% as an empty set at this level.Considering the performance of the underlying XGB and RF algorithm,the CP suggest that most of the correct classifications made by these traditional classifiers were at low confidence.The implication of classifying a sample as with multiple class is that there may be insufficient information to distinguish between rockburst grade.In such a situation,it is crucial for practitioners to carefully review the geological conditions and other relevant factors before deciding.

Fig.10.Percentage of single or multiple rockburst grade classified by the XGB-CP and RF-CP at confidence levels.

Further,single-class classifications are used to compute the efficiency of the CP,defined in this study as the percentage of singleclass classifications that are correct.To compare the efficiency of the CP across various confidence levels,a lollipop plot is presented in Fig.11.As shown in the figure,efficiency increases with confidence level.At levels of 90% and 95%,both methods obtained 100% efficiency.In comparison,the XGB-CP is more efficient since it classifies a major number of test cases at this level compared to the RF-CP.It is also comprehensible that,whiles RF-CP classified many samples as single class compared to the XGB-CP,it produced the lowest efficiency of 83% as compared to the XGB-CP of 88%.

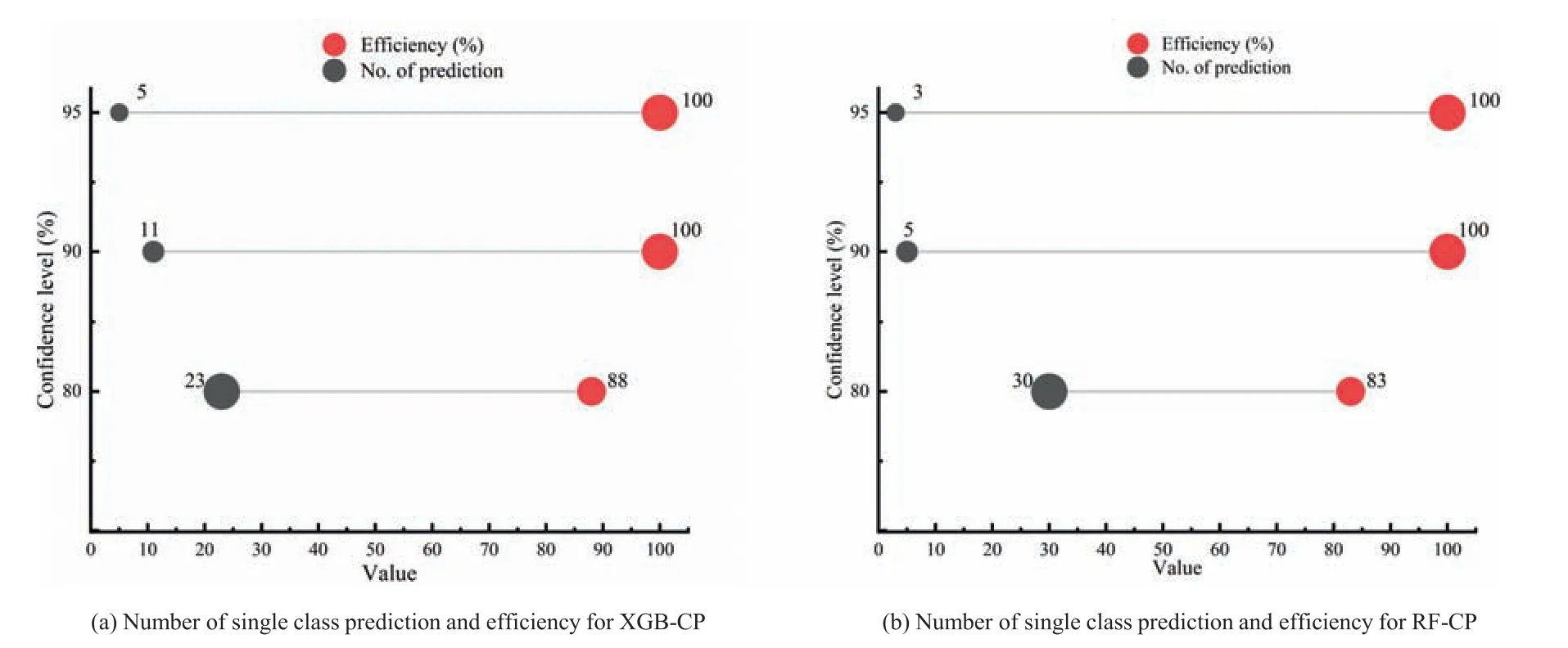
Fig.11.Lollipop plots comparing the number of single class classifications and efficiency.

4.3. Engineering application

In order to test the feasibility of the developed CP,a set of 8 rock samples from the Sanshandao Gold Mine in Shandong Province,China was utilized [46].Table 10 provides the mechanical properties and rockburst grade of these rock samples.The laboratory experiment was conducted by the original authors to evaluate ML models developed for rockburst assessment,and the details of the laboratory setup are outlined in their original publication.

Table 10 Rock mechanics parameters and rockburst grade in Sanshandao Gold Mine [46].

The results obtained are presented in Tables 11 and 12 for the XGB-CP and RF-CP respectively.From the results,the developed CP models achieves the desired marginal coverage for all confidence levels.The average classification size increases as the confidence level increases.The smallest classification set size was obtained at a confidence level of 80%.At this level,the XGB-CP and RF-CP classified 3 and 7 samples out of the 8 as one label at efficiency of 100% and 88%,respectively.

From Table 11,it is important to note that sample number 6,with a true rockburst grade of strong,was incorrectly predicted as light by the traditional XGB model,which could potentially have significant consequences in real-time applications.However,the CP model classified the sample as both light and strong grades withconfidence levels of 80% and 90%,respectively.This indicates that the sample cannot be reliably assigned a single class,as done by the traditional XGB model.In such cases,human experts would need to assess these samples to accurately label them.Interestingly,at higher confidence levels of 90% or more,the models refrained from making any single-label classifications.This implies that the correct grade of these samples cannot be confidently determined.

Table 11 The rockburst classification results in Sanshandao Gold Mine using XGB and XGB-CP.

Table 12 The rockburst classification results in Sanshandao Gold Mine using RF and RF-CP.

Given that the effectiveness of the CP is reliant on the specified confidence level,it is recommended that different confidence levels be tried to understand the performance of the classification model.It is crucial to strike a balance between reliability and efficiency.Higher confidence levels(closer to 1)will lead to more conservative predictions,with a greater proportion of correct predictions but potentially larger prediction regions.Lower confidence levels may result in more precise predictions but with the risk of increased false positives.Since rockburst is a complex and high-stake application,a higher confidence level of at least 0.80 should be used to reduce the risk of false alarms.

4.4. Advantages and limitations of proposed models

Overall,the study introduces a CP framework for rockburst classification that is capable of quantifying uncertainties associated with its classification.The CP methods demonstrated the ability to guarantee marginal coverage and,in most cases,conditional coverages with as little assumption on the data or the model as possible.The study implies that using CP in human-in-the-loop machine learning systems can provide reliable rockburst assessment with confidence estimates for each classification.Fig.12 shows a proposed framework that incorporates human validation and verification to improve the accuracy and reliability of classification models.With the proposed framework,it is possible to evaluate the coverage and size of the corresponding classification sets,in addition to standard classification accuracy measures.Moreover,the proposed framework is model agnostic,and therefore,can be used for a wide range of existing ML classifiers.However,it is important to note that the validity of CP relies on the exchangeability of the data points.If this assumption is violated,the resulting classification sets may not have the correct coverage.

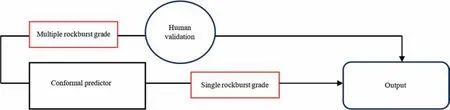
Fig.12.Proposed Human-in-the-loop framework for use in rockburst classification.

The proposed model does not directly address the forecasting aspect of rockbursts but serves as a valuable tool for assessing the potential severity of rockbursts based on known information.However,the framework can be applied to microseismic monitoring data for rockburst forecasting.The combination of ML model and physics-based methods can provide a more holistic approach to rockburst analysis.Another limitation of the study is the size of dataset used.Given that,a separate dataset is needed for training,calibration and testing,a larger database will help to produce efficient models.The CP method employed is not adaptive as it cannot guarantee conditional coverage for the various rockburst grades at a certain confidence level.Moreover,it can produce an empty classification set for uncertain rockburst instances at low confidence level.Methods such as the adaptive prediction set(APS) are recommended for future studies to improve on the bottlenecks of the proposed CP.Whiles the framework provides reliable classifications,the mechanism by which classifications are made cannot be understood as the ML models are inherently opaque.It is therefore recommended that future studies employ explainable ML methods such as Shapley additive explanation to understand the factors driving the various classifications.This is expected to foster trust in the use of the framework for rockburst assessment.

5.Conclusions

This study introduces a novel framework for rockburst assessment utilizing uncertainty quantification conformal prediction(CP) techniques and explores two CP models: XGB-CP and RF-CP.The study employs an inductive CP framework,with the dataset divided into training,calibration,and test sets.The results demonstrate that:

(1) Both CP models provide marginal coverage and,in most cases,class-wise conditional coverage.

(2) RF-CP generally produces a lower size of classification size compared to XGB-CP.At an 80% confidence level,XGB-CP and RF-CP achieve average set sizes of 1.52 and 1.21,respectively,with the size increasing as the confidence level increases.

(3) While neither model could make single label classifications at a 97% confidence level,XGB-CP classified 54%,23%,and 10% of test data as single grade at confidence levels of 80%,90%,and 95%,respectively,while RF-CP classifies 63%,10%,and 6%.

(4) The efficiency(i.e.,percentage of accurate single-label classifications) of the CP models increases with confidence level,with XGB-CP achieving 100% efficiency and RF-CP achieving 80% at confidence level of 80%.

(5) Neither CP model was able to classify any of the real rockburst cases from Sanshandao Gold Mine as a single grade for confidence levels of 90%,95%,and 97%.Nonetheless,at an 80% confidence level,XGB-CP achieved 100% efficiency,while RF-CP,which classified many samples as a single grade,achieved 75% efficiency.

Overall,the proposed CP framework can enhance the reliability and safety of the predictive models in rockburst assessment.The ability to quantify and communicate uncertainties,enables more informed decision-making and proactive risk management.It is recommended that future studies employ combined CP and explainable ML methods such as Shapley additive explanation to understand the factors driving the various classifications.This is expected to foster trust in the use of the framework for rockburst assessment.