一种窄波束测控装备车船摇隔离方法*

顾保国，郝耀峰，马东阳，周立新，屠稼木

（中国人民解放军63726 部队，宁夏 银川 750004）

0 引言

随着科学技术的发展和航天测控任务的需要，测控装备由早期单一的固定地基式发展到目前车载、船载、机载、星载等多种承载形式[1]，其中船载式和车载式都是在运动的状态下执行测控任务，即“动中测”。

船舶在海上航行或漂泊时，受风浪的影响，船载测控装备在左右、上下和前后3 个维度上都存在不同程度的晃动。对于窄波束天线来讲，由于其波束宽度一般远比船摇幅度小，如果不采取任何措施，伺服系统进行目标捕获是比较困难的[2]。与陆地固定测控装备相比，船载测控装备必须克服船摇的影响，以解决稳定问题才能实现对目标的跟踪[3]。

车载机动测控装备是对地面固定测控网点的有效补充[4]，近年来，随着电子技术的发展，一车一站式车载测控装备成为一种新的发展方向，它可以不依赖预设场地，在符合要求的公路上以车载机动的方式完成测控任务，将传统的“动中测”由海上拓展到陆地。

在“动中测”模式下，需要采取一定的措施来减小船舶和载车的晃动对天线指向的影响，所谓车船摇隔离技术，就是在“动中测”时，所采取的稳定天线指向的伺服自动控制技术。

1 车/船摇隔离技术

测控装备安装于载车、舰船等运动载体之上，由于天线转台底座与载体之间是刚性连接，运动载体自身的姿态变化将引起天线指向变化，虽然运动载体的姿态变化对天线伺服系统造成的扰动处于伺服系统位置跟踪环内，具有一定的隔离能力，但由于伺服跟踪回路带宽限制，无法对高频扰动产生理想的隔离效果，当扰动幅值大、频率高时将导致跟踪误差增大，严重时目标丢失，因而需采用一定的方法，提高伺服系统对车船摇扰动的隔离能力。车船摇隔离度就是用来衡量伺服回路对车摇或船摇扰动的抑制程度，即没有稳定措施时天线的摇摆角度与有措施时天线剩余摇摆角度的比值，一般用dB 表示，计算公式如式（1）所示：

其中，θm为没有稳定措施时天线的摇摆角度，Δθm为增加摇稳定措施后天线的剩余摇摆角度，即隔离残差。

目前在航天测量船上普遍采用的船摇隔离方法是反馈陀螺法[5]，这种方法与位置跟踪环路联合使用，船摇隔离度能达到38.8 dB 以上[6]，在幅度为7.5°的船摇情况下，隔离残差在0.08°左右，这对于波束宽度在2°以上的宽波束天线，是能够满足使用要求的；但是对于波束宽度小于0.2°的窄波束天线来说，其隔离残差几乎达到了波束宽度的一半，是无法满足正常跟踪需求的。本文所研究的窄波束测控装备，其天线波束宽度为0.2°，船摇隔离度的指标要求是不小于50 dB（船横摇±7.5°、周期8 s，纵摇±3.0 °、周期5.5 s），车摇隔离度不低于20 dB（车摇±1 °，周期0.5 s）。

2 伺服系统建模

伺服系统通常包含电流环[7−9]、速度环[10−11]、位置环[12−15]（也称作“位置跟踪环”或“跟踪环”）。为了便于对车载/船载测控装备的伺服系统动态性能进行分析与评估，建立包含电流环、速度环和位置环的模型，如图1所示。为了使模型更接近真实情况，该模型还包括了负载天线等效的转动惯量与摩擦力。

图1 伺服系统模型

3 船摇隔离度分析

在进行船摇隔离度的仿真分析时，采用等效的正弦信号代替真实的船横摇与纵摇，其中横摇为幅值7.5°、周期8 s 的正弦信号，纵摇为幅值3.0°、周期5.5 s 的正弦信号。为评估伺服系统对船摇扰动的最大隔离能力，假设横摇、纵摇扰动量全部叠加在天线轴上。

3.1 仅采用位置环的船摇隔离度分析

在位置跟踪回路中增加上述的正弦信号来代替船摇扰动，隔离度仿真结果分别如图2 和图3 所示。

图2 仅位置回路策略下横摇隔离仿真结果

图3 仅位置回路策略下纵摇隔离仿真结果

从结果中可以看出：对于方位轴，横摇隔离残差为0.182°，隔离度约为32.3 dB，纵摇隔离残差为0.155°，隔离度约为25.7 dB；对于俯仰轴，横摇隔离残差为0.169°，隔离度约为32.9 dB，纵摇隔离残差为0.143°，隔离度约为26.4 dB。仅仅依靠位置环，横摇和纵摇的隔离残差均超过窄波束天线的半波束宽度，无法满足跟踪要求。

3.2 叠加船摇前馈补偿的船摇隔离度分析

为进一步提高伺服系统的船摇隔离度，在位置环的基础上叠加船摇前馈补偿策略。利用安装于天线座底部的惯导来测量船摇，通过坐标变换计算出船摇引起的在天线方位、俯仰轴上的扰动速度分量，并将该速度信号馈入速度回路输入端，以进行速度补偿。惯导安装时，惯导坐标系与船体坐标系重合，船体坐标系示意图如图4 所示，其中ωH为航向角速度，ωR为横摇角速度，ωP为纵摇角速度。

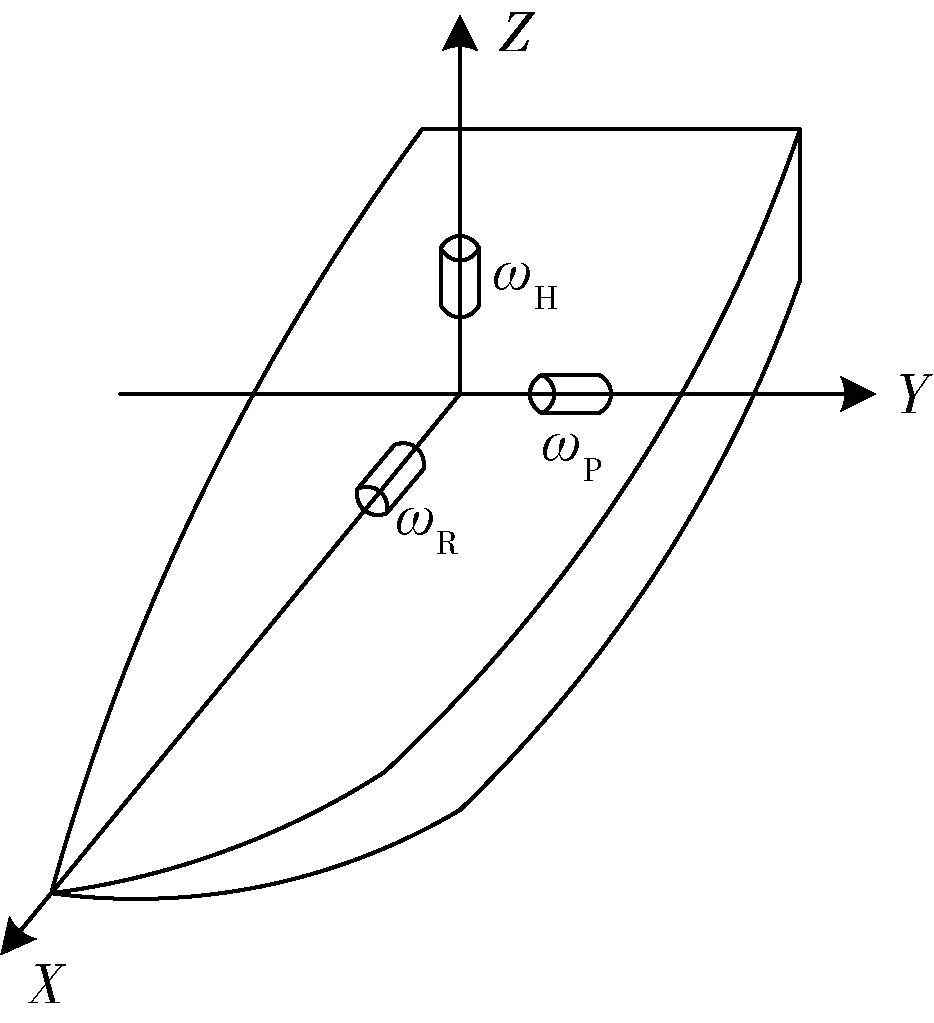
图4 船体坐标系示意图

在此坐标系下，船摇在方位轴上的扰动角速度分量为：

在俯仰轴上的扰动角速度分量为：

叠加船摇前馈补偿后的仿真结果如图5 和图6所示。

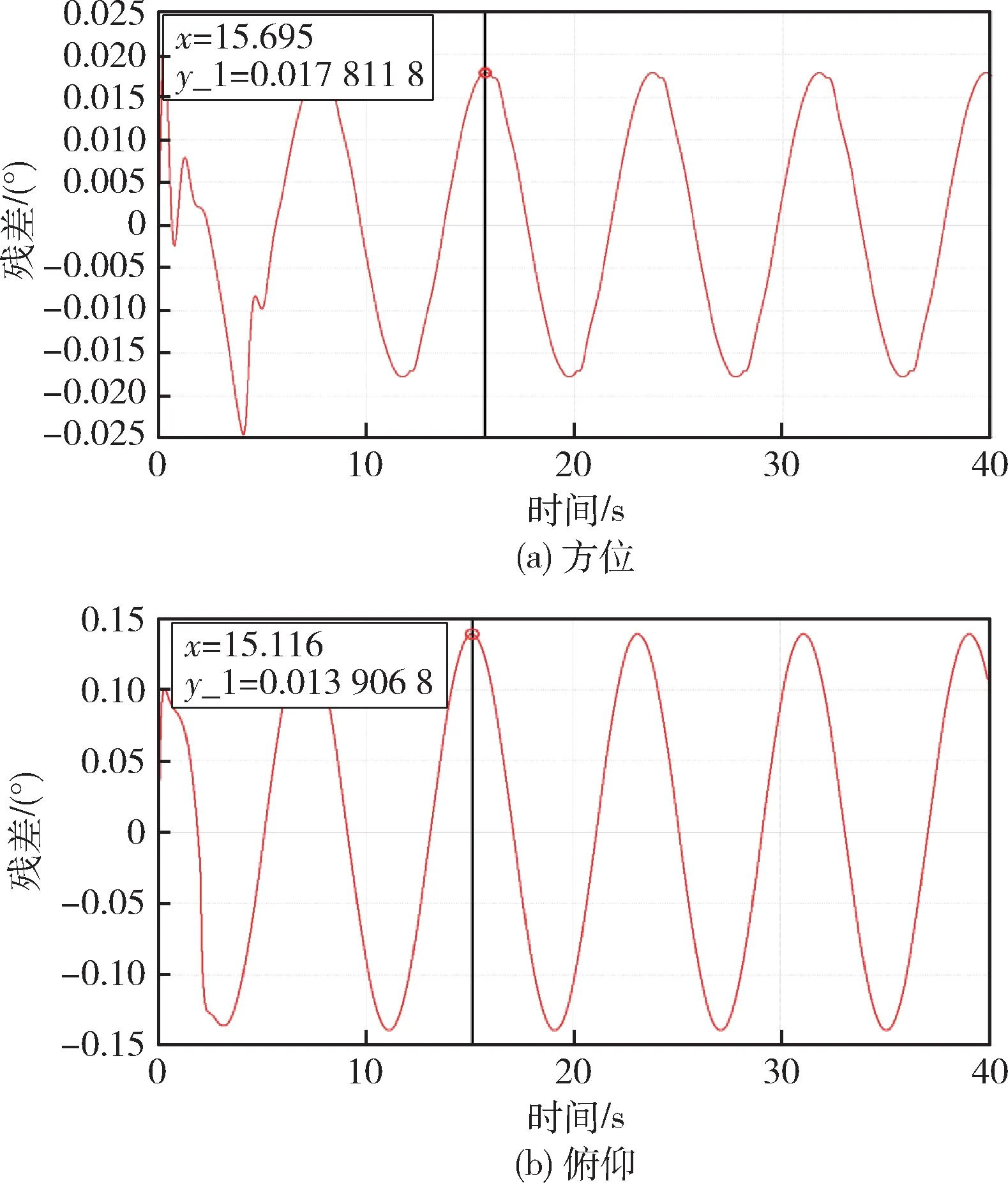
图5 船摇前馈补偿策略下横摇隔离仿真结果

图6 船摇前馈补偿策略下纵摇隔离仿真结果

从图5 和图6 中可以看出，叠加船摇前馈补偿策略后，方位轴横摇隔离残差减小到0.018°，隔离度约为52.4 dB，纵摇隔离残差减小到0.016°，隔离度约为45.5 dB；俯仰轴横摇隔离残差减小到0.014°，隔离度约为54.6 dB，纵摇隔离残差减小到0.012°，隔离度约为47.9 dB，伺服系统船摇隔离度指标显著提高。由于系统隔离度与扰动频率相关，频率越高隔离能力越弱[16]，纵摇扰动频率比横摇高，因而其隔离度低一些。

3.3 叠加陀螺稳定环的船摇隔离度分析

经上一节仿真分析，在采用叠加船摇前馈补偿后，伺服系统船摇隔离度指标显著提高，为进一步提高伺服系统的船摇隔离度，通常考虑在船摇前馈补偿的基础上，增加陀螺稳定环[17]。

陀螺稳定环介于速度环与位置环之间，是一个反馈稳定回路。利用陀螺空间测速机的原理，将双轴速率陀螺安装于天线背面的基准面上，直接感应方位、俯仰轴在惯性空间的转动角速度信息，并进行反馈控制，构成陀螺稳定环。在实际应用中，设有“无陀自跟踪”工作方式，就是在船摇不是很严重的条件下，断开陀螺环，以保证跟踪性能。即，建立陀螺稳定环来提高抗船摇扰动的能力是要以牺牲一些跟踪性能为代价的。在船摇前馈补偿策略的基础上，增加陀螺稳定回路的仿真模型如图7 所示，仿真结果如图8 和图9 所示。

图7 陀螺稳定策略下仿真模型

图8 陀螺稳定策略下横摇隔离仿真结果

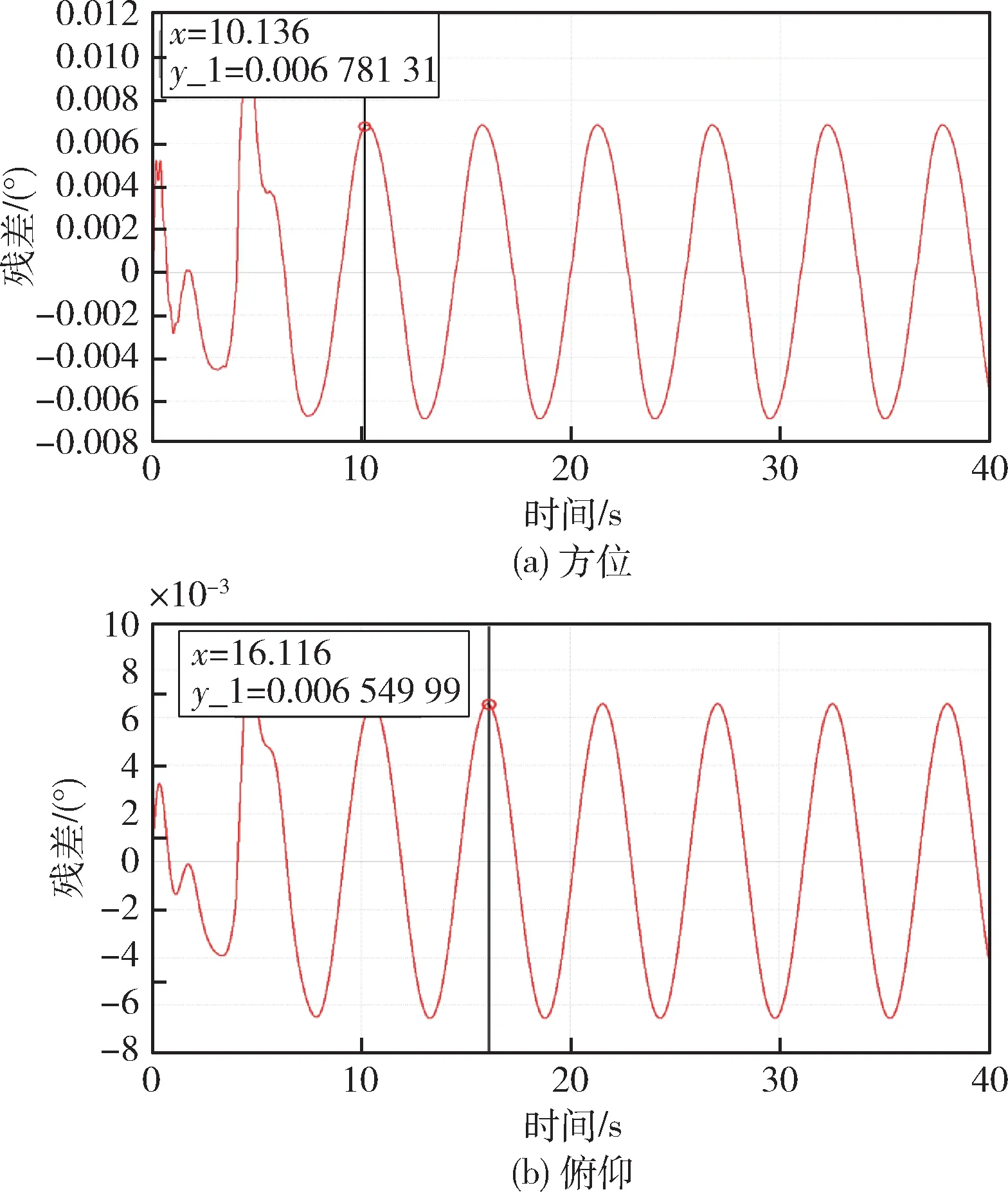
图9 陀螺稳定策略下纵摇隔离仿真结果

从图8、图9 中可以看出，采用“位置环路+船摇补偿+陀螺稳定”的隔离策略之后，方位轴横摇隔离残差减小到0.005 53°，隔离度约为62.6 dB，纵摇隔离残差减小到0.006 8°，隔离度约为52.9 dB；俯仰轴横摇隔离残差减小到0.005 50°，隔离度约为62.7 dB，纵摇隔离残差减小到0.006 5°，隔离度约为53.3 dB，隔离船摇的能力进一步提高[18]。

3.4 仿真小结

综合上述仿真结果，该伺服系统船摇隔离度仿真结果汇总如表1 所示。

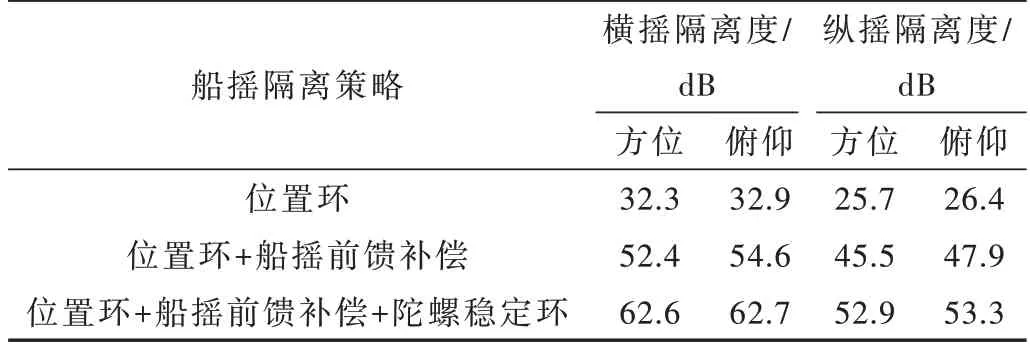
表1 船摇隔离度仿真结果

在采用“位置回路+船摇前馈补偿”的策略，方位与俯仰的横摇隔离度均能够达到50 dB、纵摇隔离度达到45 dB；再增加陀螺稳定环设计，则横摇隔离度能够达到约62 dB，纵摇隔离度约52 dB，能够满足窄波束天线的跟踪要求。

4 车摇隔离度分析

在伺服控制系统的结构及参数固定时，系统对扰动的隔离度只与扰动的频率有关，无论是车摇还是船摇，在相同的扰动频率下，其扰动隔离度是固定的。通常情况下，船摇的扰动频率较低，相应的系统隔离能力较强，隔离度较高；而车摇的扰动频率相对较高，相应的系统隔离能力变弱，隔离度较低，但是车摇的扰动幅度比船摇小。

4.1 仅采用位置环的车摇隔离度分析

对于机动平台的测控装备来说，无论是车载模式还是船载模式，其伺服系统是完全相同的。当仅使用位置跟踪回路对车摇扰动进行隔离时，根据图1 所示的模型，在扰动幅度均为1°的情况下，可得到不同扰动频率下的隔离度，仿真结果如表2 所示。

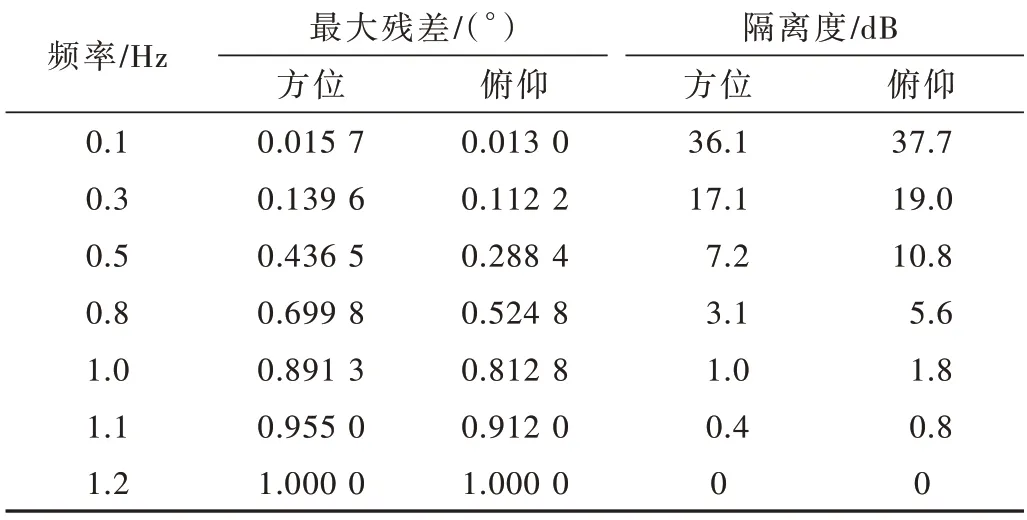
表2 位置环车摇隔离度仿真结果

从表2 中可以看出，仅使用位置跟踪回路进行扰动隔离，当扰动频率为0.1 Hz 时，方位、俯仰隔离度分别为36.1 dB 和37.7 dB；当扰动频率为1 Hz 时，方位、俯仰的隔离度下降为1.0 dB 和1.8 dB；当扰动频率上升为1.2 Hz 时，隔离度为0，已没有扰动隔离能力。因此，在仅仅使用位置跟踪环路进行隔离时，无法满足车载状态下的隔离度要求，需要使用额外的隔离措施，以提高系统扰动隔离能力。

4.2 叠加前馈补偿的车摇隔离度分析

与船摇前馈补偿方法相同，可利用车摇速率补偿，即通过安装于天线座底盘上的惯导系统实时检测车摇扰动速率信号，并将其馈入系统速度回路，以补偿扰动速率的影响，提高车摇隔离度。采用车摇前馈补偿策略，不同扰动频率下的隔离度仿真结果如表3 所示。

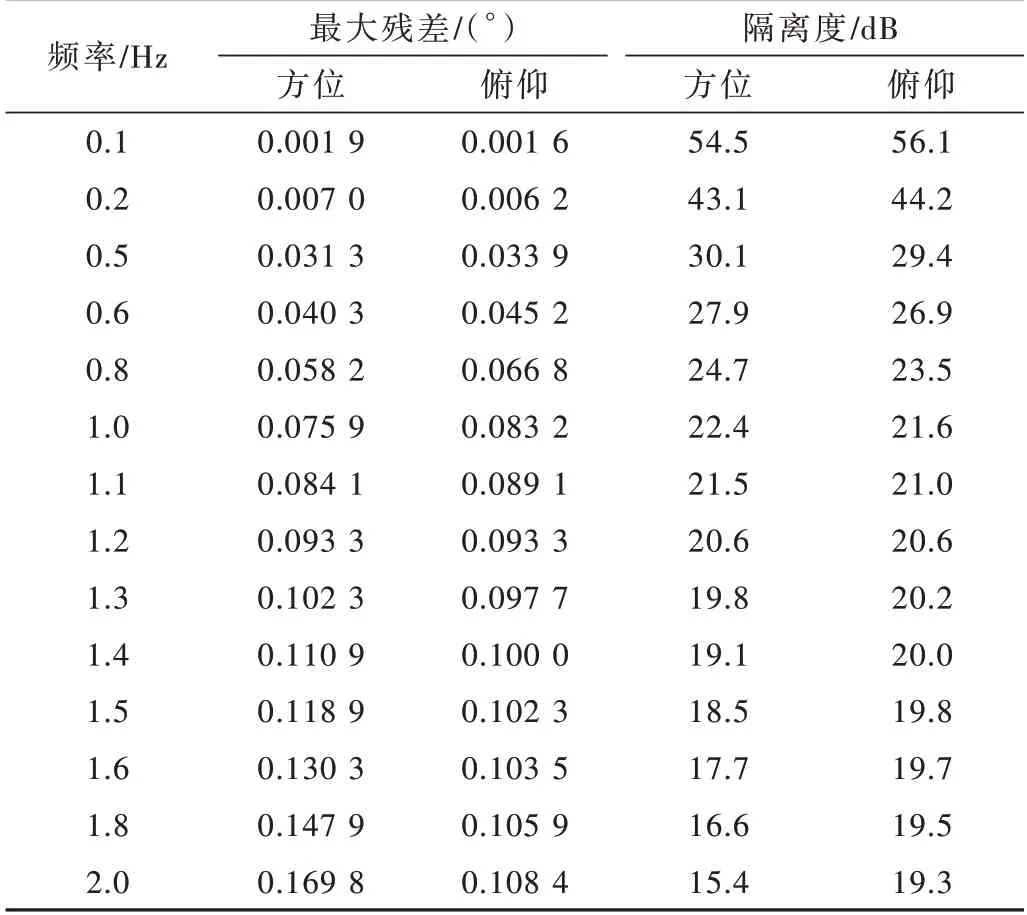
表3 叠加车摇前馈补偿隔离度仿真结果

从结果中可以看出，叠加车摇前馈补偿后，当扰动频率小于1.5 Hz 时，俯仰隔离度满足20 dB 要求，扰动频率为2 Hz 时隔离度为19 dB 左右；因方位转动惯量远大于俯仰转动惯量，导致方位高频响应要慢一些，其隔离度在扰动频率小于1.3 Hz 时能达到20 dB，当扰动频率为2 Hz 时隔离度约为15 dB，仍然不能满足指标要求。

4.3 叠加陀螺稳定车摇隔离度分析

在车摇前馈的基础上叠加陀螺稳定回路，仿真结果如表4 所示。

表4 增加陀螺稳定回路后的车摇隔离度仿真结果

从仿真结果中可以看出，在扰动幅度为1°时，当车摇扰动频率在2 Hz 以内时，方位与俯仰支路的隔离度均能达到20 dB，满足指标要求。

4.4 车体隔振处理

与船摇相比，车摇扰动的频率较高，隔离难度大，通过使用不同控制策略的隔离效果改善很有限。因而，考虑对载车和方舱采取一定的隔振措施，使整车的扰动频率变为2 Hz 以内，则根据前述仿真结果，此时车摇隔离度可达到20 dB 左右。

4.5 仿真小结

车摇扰动频率比船摇情况下要高，隔离问题复杂，实现难度大。仿真结果表明，采用“位置环+车摇前馈+陀螺稳定环路”的车摇隔离策略时，当车摇扰动频率小于2 Hz 时，方位支路的车摇隔离度可达到 20.1 dB，俯仰支路的车摇隔离度可达到 22.7 dB，满足指标要求。

5 伺服系统动态跟踪性能分析

假定目标高度为10 km，以5 Ma 速度直线匀速飞行，航捷（即测站与目标的距离最近距离）为10 km，最远距离为100 km，此时天线跟踪目标的方位角速度如图10 所示。

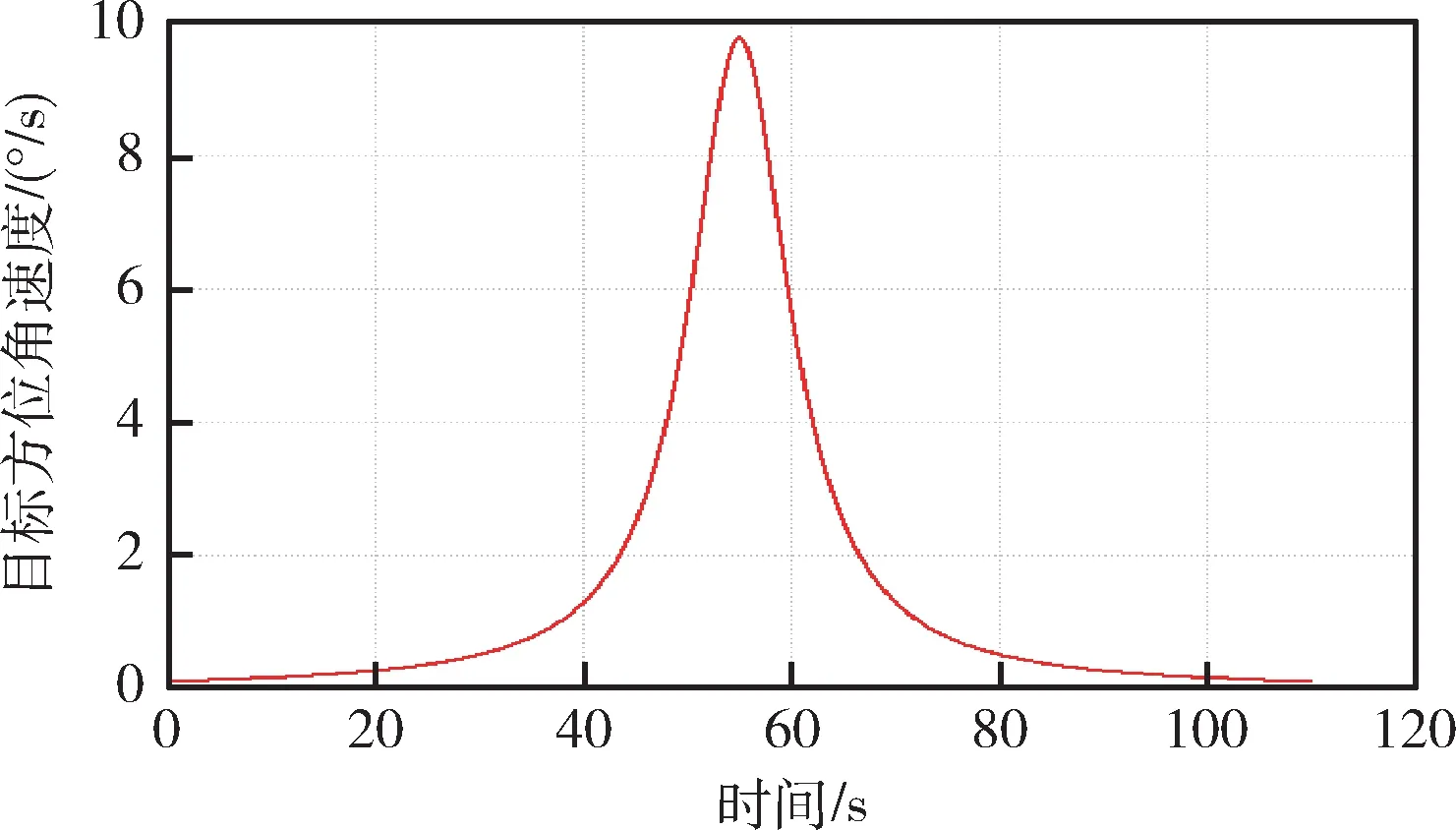
图10 目标方位角速度曲线

在过航捷点，角速度达到最大值，在目标跟踪过程中，伺服系统需要同时实现对目标的精确跟踪和船摇扰动抑制。

假设在跟踪过程中，船摇始终对方位产生幅值7.5°、周期8 s 的正弦波扰动，根据3.3 节所述的模型，仿真结果如图11 所示。

图11 船摇扰动下的目标动态跟踪方位误差

仿真结果表明，未到达航捷点附近时，跟踪误差峰值小于0.01°；到达航捷点附近时，跟踪误差峰值约为0.02°，整个目标跟踪过程中的跟踪误差均方根值约为0.007 2°，满足窄波束天线的跟踪要求。

6 结论

在“动中测”的测控需求下，隔离载车或者舰船的摇摆对测控天线的影响，使得天线不受车体或船体的摇摆而摇摆，保证天线空间指向的稳定性，是车载/船载伺服系统设计的关键所在。本文针对车载/船载窄波束测控装备的跟踪需求，建立经典的电流环、速度环和位置环伺服系统模型，分别采用“仅位置环”“位置环+车船摇前馈补偿”和“位置环+车船摇前馈补偿+陀螺稳定环”3 种策略，在船舶横摇±7.5°、周期8 s，纵摇±3.0°、周期5.5 s，车摇±1°、周期0.5 s 的条件下进行仿真分析，仿真结果表明，采用“位置环+车船摇前馈补偿+陀螺稳定环”的车船摇隔离方法，横摇隔离度方位62.6 dB、俯仰62.7 dB；纵摇隔离度方位52.9 dB、俯仰53.3 dB；车摇隔离度方位20.1 dB、俯仰22.7 dB；对飞行高度为10 km，航捷为10 km，以5 Ma 飞行的高速目标的角度跟踪误差小于0.007 2°，能够满足窄波束测控设备的跟踪要求。