基于流水线的RSA 加密算法硬件实现*

杨龙飞，卢 仕，彭 旷

（湖北大学 微电子学院，湖北 武汉 430062）

0 引言

从古到今，信息安全都是一项值得注意的问题，如今也有许多可考究的古代密码学的应用。直到1976 年，几乎所有的加密方法都是同一种模式：加解密使用同样的密钥。但在1976 年两位美国计算机学家提出了Diffie-Hellman 密钥交换算法，非对称加密算法便由此诞生[1−2]。非对称加密算法有两个不同密钥——公钥和私钥，公钥用来加密明文，私钥用来解密密文。而RSA 加密算法便是非对称加密算法中的一种。密码学不断发展的今天，RSA 加密算法已经成为国际公认的比较理想的一种加密算法[3−5]。

在RSA 的安全性研究上已经比较深入了，有不少提高安全性的手段，如使用SMM 算法，改进算法的结构，增加质数的个数等方法[6−8]。但提高安全性的最简单手段就是提高RSA 加密位数，目前推荐使用1 024 位的大数进行数字加密可以获得良好的安全性。且在RSA 加密算法一般使用蒙哥马利算法完成大数计算，但硬件完成基于蒙哥马利算法的RSA 加密，存在着硬件实现成本较高、运算时间较长等问题。本文针对以上问题实现了一种基于流水线形式的蒙哥马利算法，并行运算RSA 加密算法，提高了其工作的频率，加快了其运算的速度。

1 算法介绍

1.1 RSA 加密算法

RSA 加密算法是3 位数学家1977 年提出的非对称密码体制，其主要步骤如下：先选择2 个大素数p和q，然后求出它们的乘积n以及欧拉函数φ(n)=(q−1)·(p−1)；接着选择一个加密密钥e，满足1 ＜e＜φ(n)且e与φ(n)互质；在保证(e，n)作为公钥对外公开之后，利用公式c=me%n将明文m加密为密文c；此后，将密文发送给接收者进行解密，在保证(d，n)作为私钥仅为接收者所知之后，利用公式m=cd%n将密文c解密为明文m获取信息[9−10]。

RSA 算法可以同时应用于数字签名和加密，由于RSA 加密算法的加解密过程在公式上的一致性，故本文主要研究的是RSA 加密算法的加密过程c=me%n。

1.2 蒙哥马利模乘算法

RSA 加密算法中所运算的数是1 024 位以上的大数，因此无法直接进行模幂运算。在RSA 中，模幂的运算速度是限制RSA 加密速度的关键因素之一。模幂本质上是除法运算，但除法运算是又是四则运算中最耗时的一种运算方式，因此如何通过优化除法运算来加速RSA 运算速度是非常重要的一步。1985 年，Peter Montgomery 发现了一种灵巧的算法，该算法只需要通过乘法和数的位移就可以实现模乘运算，这就是著名的蒙哥马利模乘算法[11]。

（1a）的q用来补偿（1b）中余数被舍弃的问题，其中N[0]·N[0]'%r=1，解q的问题等价于求解二元一次方程A·B−N·M=1 中的最小整数解，其中A=C[0] +A[i]·B[0]，N=r，M=r−N`[0]。借助辗转相除法，可以计算出B的值，从而得到q的解。特别地，当r=2 时，q=C[0] +A[i]·B[0][13]。

在文献[14]中提出了其中r=2 的CSA 改进蒙哥马利算法，使用选择器代替乘法，使用CSA 链完成大数的计算，其算法过程如下所示，其中SUM 和CRY 表示CSA链计算出的和与进位，CSA_ADD 表示使用CSA 链计算2 个大数的和，B_N表示B和N的总和：

以上代码中，为了避免出现C超过N的情况，运行时需要进行两次额外的循环，整个计算过程只需要一个CSA 链实现。CSA 改进的蒙哥马利算法的硬件结构如图1 所示。在计算中，每一轮循环只能计算一位数据。对于一个n位的数据，最后需要n+2 个周期才能得到结果，因此需要较长时间的运算。

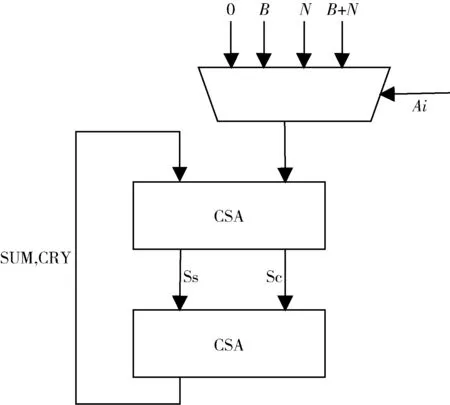
图1 CSA 改进蒙哥马利算法

为了提高蒙哥马利算法的计算速度，在文献[15]中提出了一种r=4 的蒙哥马利算法，在计算时将乘法转换成了加法，下文称MON4，其硬件结构如图2 所示。代码如下其中Bc 和Bs 是上一级蒙哥马利模块输入的数据，Sc、Ss 以及Zc、Zs 分别是从CSA 输出的和与进位：

在上述的算法中一次迭代会计算A中的两位数，所以比二进制的蒙哥马利算法的迭代次数少一半，运算的速度提升了一倍。

而且在硬件实现中做了以下的优化：

（1）在预处理之后使用一个选择器完成（3c）与（3d）中的形如2·A[2i+1]·Bs +A[2i]·Bs 的乘加计算，省去了乘法运算，降低了逻辑复杂度。

（2）使用CSA 加法器完成大数的计算，（3c）使用一个了CSA 加法器，（3d）使用两个了CSA 加法器，可以快速地完成大数运算。

当实现了上述的蒙哥马利算法之后可以将RSA 加密算法改写成以下计算：

可以看出，其中最重要的就是C=MON(C,M)与M=MON(M,M)两个大数相乘求余的算式。在当前的ei下进行运算时，M值之间没有先后顺序的关系。也就是，M的平方模乘和(C，M)模乘在计算时是相互独立且不会互相影响的。因此，在硬件实现中，一般可以采用两个模乘器，让平方和模乘两个操作在一个时钟周期内并行执行，以达到省时和提速的目的[16−17]。

1.3 改进的高进制蒙哥马利算法

文献[15]在实现RSA 加密算法的四进制蒙哥马利算法中，采用R-L 的并行迭代形式，需要两个相同的四进制蒙哥马利算法模块，共需6 个CSA 链。当计算1 024位的大数加密时，一个CSA 链需要一千多个CSA 模块，因此需要大量的硬件资源。此外，该模块的关键路径较长，无法以较高的频率工作。针对以上的情况，本文改进了四进制蒙哥马利算法，下文称PMON，其中Sc、Ss以及SUM、CRY 同样是CSA 链输出的和与进位：

在进行蒙哥马利算法的预处理阶段中，按照文献[15]的方法计算3·B和3·N的值。此时，仅需使用一级CSA 链即可完成（4a）的计算。对于q的求解，可观察到（4a）中 的C[0] +A[i]·B[0]即 为Sc 和Ss 低两位之和。这可以直接利用（4a）计算的结果得出。在计算（4c）时，同样只需要使用一个一级CSA 链。相关结构示意图如图3 所示。进行四进制蒙哥马利算法的改进后，考虑到RSA 加密算法需要同时计算M=MON(M,M) 以及P=MON(P,M)，还是需要两个此类模块，因此本文引入了流水线机制，并将所需的两个蒙哥马利模块合并为一个。

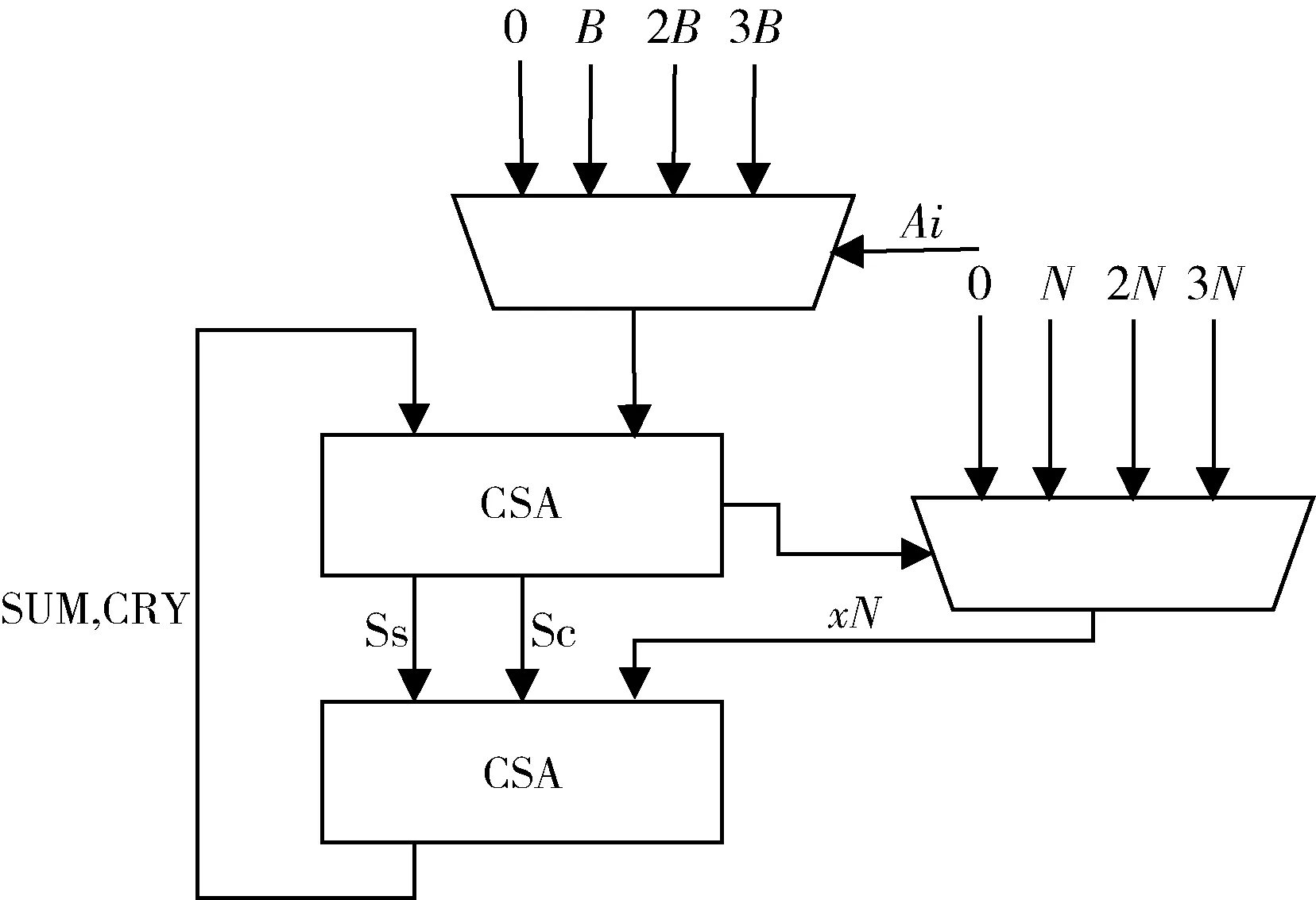
图3 改进的蒙哥马利算法

在（4b）和（4c）中加入寄存器片将计算划分为P1 和P2 两部分，P1 具有一个CSA 链和一个选择器，P2 具有一个用于计算SUM[i+1]和CRY[i+1]的CSA 链。如图4所示，在第X个时钟周期中，P1 负责计算M=PMON(M,M) 中的（4b）和（4c）部分，而P2 负责计算P=PMON(P,M)中的（4d）部分；在第X+1 个时钟周期中，P1负责计算M=PMON(M,M) 中的（4b）和（4c）部分，而P2负责计算M=PMON(M,M)中的（4d）部分。重复以上过程直到计算完成。

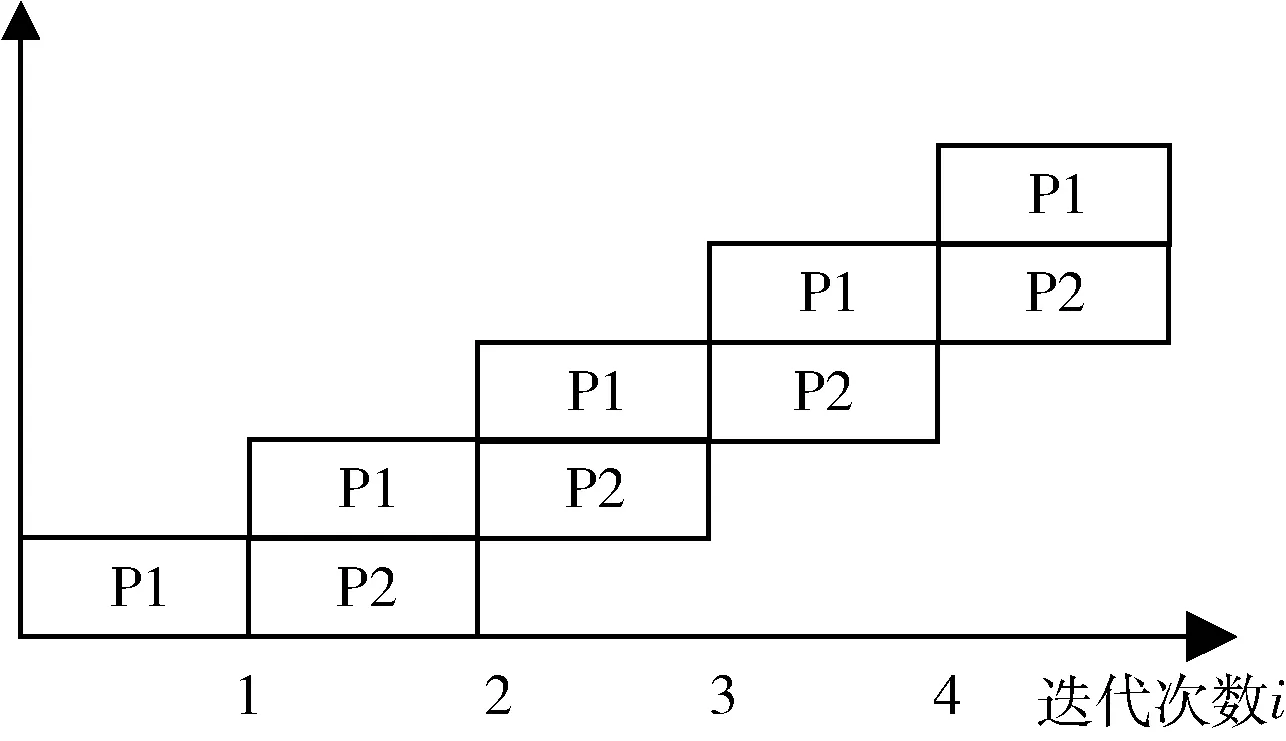
图4 蒙哥马利算法的流水示意图

在预处理以及后处理部分需要两个32 位CPA 加法器，在开始时使用CPA 加法器计算2M+M以及2N+N的值，在结束时分别计算流水线出来的两级SUM[m/2 +1]+CRY[m/2+1]，最 后RES_PM 与RES_MM 即 为PMON 模块的输出结果。

表1 列出了PMON（本文）与MON4（文献[15]）两种蒙哥马利算法实现RSA 加密算法硬件模块的一些性能参数，n表示计算RSA 加密算法的位数，k表示指数E的位数。使用PMON 计算1 024 位的RSA 加密算法时，考虑最坏的一种情况，即E的宽度也是1 024 位时，使用PMON 完成一次RSA加密需要1 090×1 026=1.12 M 个时钟周期，在50 MHz 的时钟下一秒可以完成44 次RSA加密。

表1 文献[15]与本文方案对比

2 性能分析

本文基于Xilinx 公司XC7K410T 系列的FPGA 开发板，实现了蒙哥马利算法以及RSA 加密算法，并用Python 实现了相同的算法。为了验证其正确性，本文首先使用Python 计算C=ME%N完成加密过程，然后计算Q=CD%N完成解密过程，若M与Q相等则证明Python编写的算法正确。接着，使用VCS 工具对硬件代码进行仿真，将其结果与Python 代码的输出结果进行对比，从而验证RTL 实现的RSA 加密算法在功能上的正确性。

使用以下的数据对模块做正确性判定：M=0x1538ebf833ffca2a01d6099faccea21238473afba693cba06 3edfe4c6a420c20；E=65537；N=0x439aeab34eaee973e968 ebdd11d6d3ef7302072c4bfd4f7fe2b0cf9889277f6d；求 出私钥D=0x2a66af6d669c2daf956549098e76becfae00a8dd7 50ffe85c9c795776014b601。其计算过程如图5 所示，可以看出最后计算的Q与M相等，可以验证Python 代码的正确性。然后查看Verilog 代码的仿真波形将其输出结果与Python 代码的输出结果做对比。从图6 可以看出最后的输出结果output_data 与上述结果相同。

图5 RSA 加密算法结果示意图

图6 RSA 加密算法仿真波形图

表2 对比了本文所设计的RSA 加密算法模块和其他文献设计方案在对1 024 位大数进行加密时的相关数据。除了文献[18]中在最大工作频率超过本文的方案外，本文的方案表现出了资源占用更少和工作频率更高的特点。与文献[18]相比，本文的方案所占用的资源更少，频率也没有显著下降，因此本文设计的RSA 加密模块已经达到了优化的目标。

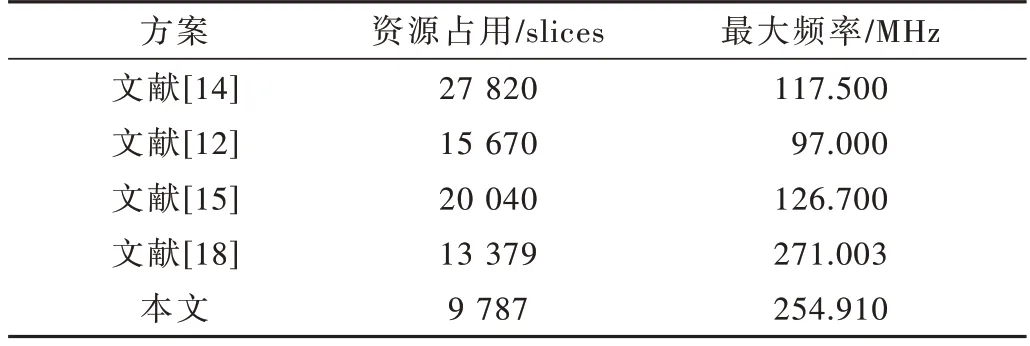
表2 各种方案的性能对比

3 结论

本文对四进制蒙哥马利模算法进行了优化，实现了硬件资源的节约，减少了关键路径，并在计算RSA 加密算法过程中引入了流水线。在此基础上，完成了RSA 加密算法模块的RTL 代码构建，并进行了仿真验证。最后，与相关的一些RSA 加密算法模块的设计进行了性能分析。未考虑拓展性及功耗等方面，下一步需要进行模块参数化的调整，使该模块的加密能力不仅限于1 024位，并进行功耗等性能的优化。