一类微分系统变号解的存在性和多解性

张慧星, 高 妍, 姚香娟

(中国矿业大学 数学学院 江苏 徐州 221116)

0 引言

本文研究基尔霍夫-薛定谔-泊松系统

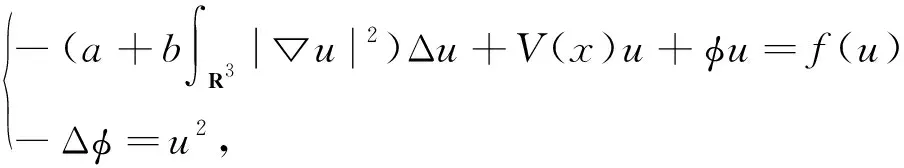
(1)

变号解的存在性与多解性, 其中:x∈R3;a,b>0。 当a=1,b=0时, 系统(1)变为薛定谔-泊松系统,

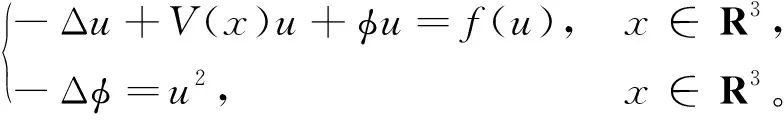
(2)

从物理学的角度来看, 系统(2)广泛应用于量子电动力学和半导体理论等领域, 可用来描述粒子在空间和时间上的运动规律, 代表了带电粒子与静电场相互作用的模型, 它存在驻波解。 关于薛定谔-泊松系统, 近年来最主要的研究集中于寻找它的非平凡解,也有一些学者研究了它的变号解情况[1-5]。文献[6]利用下降流不变集方法结合抽象临界点理论, 给出了薛定谔-泊松系统变号解的存在性和多解性。本文研究更一般的基尔霍夫-薛定谔-泊松系统解的存在性和多解性。

假设V∈C(R3,R+)满足如下条件。

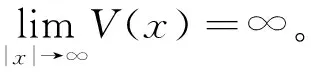
对于非线性项f, 我们有如下假设:

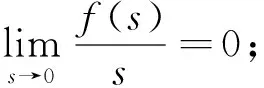
本文的主要结果如下。

定理1如果条件V0)和假设f1)～f3)成立, 则基尔霍夫-薛定谔-泊松系统存在至少一个变号解。 如果f(u)是奇函数, 则此系统存在无穷多个变号解。

1 预备知识

下面给出φu的一些相关性质。

引理1[6]φu有如下性质。

1)φu(x)≥0,x∈R3;

2)存在与u无关的C>0, 使得

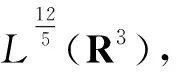
定义Sobolev空间

它的范数定义为

这是一个Hilbert空间, 内积表示为

我们定义算子

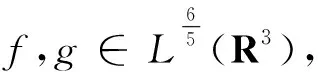
D(uv,uv)2≤D(u2,u2)D(v2,v2)。

把φ=φu代入系统(1), 可将系统(1)转化为

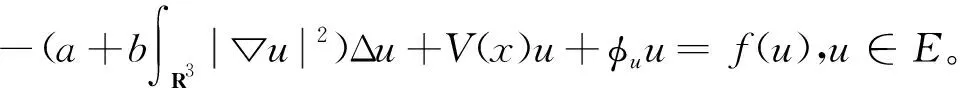
(3)

定义E上的能量泛函I为

易知I∈C1(E,R),且∀u,v∈E,

下面我们将证明方程(3)的变号解的存在性和多解性, 从而进一步得到基尔霍夫-薛定谔-泊松系统变号解的存在性与多重性。

2 构造辅助算子A

我们引入辅助算子A, 用它来构造泛函I的下降流。 ∀u∈E, 定义v=A(u)∈E是方程

(4)

的唯一解。 显然,u是式(3)的解,等价于u是I的临界点, 也等价于u是A的不动点。

引理3算子A是连续紧算子。

证令u∈E, 且定义

则J0∈C1(E,R)。 由假设f1)～f2)和注1,J0是强制、有下界、弱下半连续、严格凸的。 因此,J0有一个唯一极小值v=A(u)∈E, 它是式(4)的唯一解, 且A将有界集映成有界集。

接下来, 我们证明算子A是连续的。 取{un}⊂E,u∈E,且有un→u于E。 令v=A(u),且vn=A(un), 有

f(un))(v-vn)=I1+I2+I3。

对于I1, 由Hölder不等式及注1, 有

对于I2, 因|·|≤|·|E,由引理1和引理2, 有

C3‖un-u‖E·‖v-vn‖E。

设g1(t)=φ(t)f(t),g2(t)=f(t)-g1(t),则由假设f1)～f2)知, 存在C4>0, 使得对任意的实数s, 有

|g1(s)|≤C4|s|,且|g2(s)|≤C4|s|5。

因此,

综上,

进一步,有

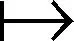
和

进一步,

综上, ‖v-vn‖E→0, 即A是连续算子。

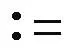
-(a+bM)Δv+V(x)v+φuv=f(u)

的弱解, 因此

考虑

由Fatou引理,有

下面证明

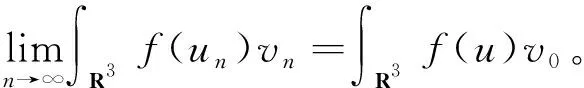
(5)

因为

由于在L4(R3)中,vn→v0, 有

此外

因为un→u于L4(R3), 当n→∞时, 且un,vn都是E中有界序列, 所以存在C7>0, 使得

由ε的任意性, 有

综上, 由范数的等价性可知, 当n→∞时,vn→v0于E。 即A是紧算子。

注2若f是奇的, 则A也是奇的。

证明1) 因为A(u)是式(4)的解, 则

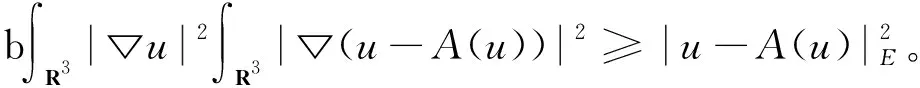
所以

2) 对任意φ∈E, 有

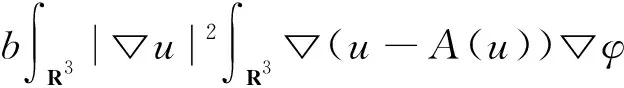
‖u-A(u)‖E·‖φ‖E。

所以, 对任意u∈E,

‖I′(u)‖=sup‖φ‖=1〈I′(u),φ〉≤

引理5∀a0, 若∀u∈E,I(u)∈[a,b],且|I′(u)|≥α, 则∃β>0, 使得‖u-A(u)‖E≥β。

证明∀u∈E, 由假设f3),有

因此, 有

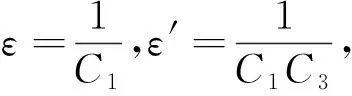
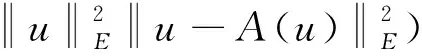
(6)

成立,假设存在{un}∈E, 当I(u)∈[a,b],且|I′(u)|≥α时, 有‖un-A(un)‖E→0,n→∞。 则由式(6)知, {‖un‖E}是有界的。 再由引理4的2), 得出矛盾。

3 构造下降流不变集

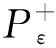
引理6∃ε0>0,使得∀ε∈(0,ε0), 有:

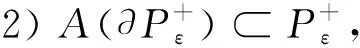
证明这里只证明引理6的1), 2)同理。 记u∈E为u=u++u-, 其中:u+=max{u,0};u-=min{u,0}。 对u∈E, 记v=A(u)。 由注1可知, 对任意q∈[2,6], 存在mq>0,使得

成立,且

由假设f3)和Hölder不等式, 有

dist(v,P-)‖v+‖E≤(v,v+)E≤δ‖u+‖2‖v+‖2+

Cδdist(u,P-)p-1)‖v+‖E。

因此, 有

dist(v,P-)≤C(δdist(u,P-)+Cδdist(u,P-)p-1)。

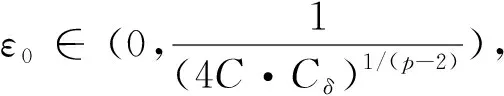
用K表示A的不动点集, 它也是I的临界点集。 因为A仅是连续的, 我们需要在E0=EK上构造局部Lipschitz连续的算子B,B需具有A的主要性质。 有如下结论[11]。

引理7存在一个局部Lipschitz连续的算子B:E0→E, 使得

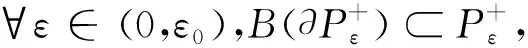
4) 若f是奇的, 则B是奇的。

4 定理1的证明

4.1 定理1的存在性部分

我们采用包含下降流的不变集的极小极大方法证明系统(3)至少存在一个变号解。 首先, 引入一些基本结果。

令X是一个Banach空间,J∈C1(X,R),P,Q⊂X是开集,M=P∩Q,Σ=∂P∩∂Q,且W=P∪Q。∀c∈R,Kc={x∈X:J(x)=c,J′(x)=0},且Jc={x∈X:J(x)≤c}。

定义1[10]假如下面形变性质成立, 若KcW=∅, 则∃ε0>0,使得∀ε∈(0,ε0), 存在η∈C(X,X)满足:

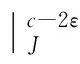
3)η(Jc+εW)⊂Jc-ε;

则对J来说,{P,Q}被称为是可容许的在能量级c的不变集。

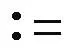
1)φ0(∂1Δ)⊂P,且φ0(∂2Δ)⊂Q;

2)φ0(∂0Δ)∩M=∅;

其中:Δ={(t1,t2)∈R2:t1,t2≥0,t1+t2≤1};∂1Δ={0}×[0,1];∂2Δ=[0,1]×{0};且∂0Δ={(t1,t2)∈R2:t1,t2≥0,t1+t2=1}。 定义

其中

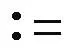
Q,φ|∂0Δ=φ0|∂0Δ},

则c≥c*且KcW≠∅。

引理9若KcW=∅, 则存在ε0>0,使得对0<ε<ε′<ε0, 存在一个连续映射σ:[0,1]×E→E满足:

1) ∀u∈E,σ(0,u)=u;

2) ∀t∈[0,1],u∉I-1[c-ε′,c+ε′],σ(t,u)=u;

3)σ(1,Ic+εW)⊂Ic-ε;

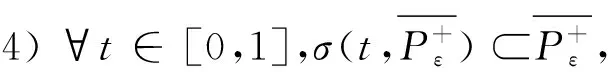
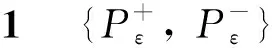
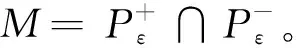
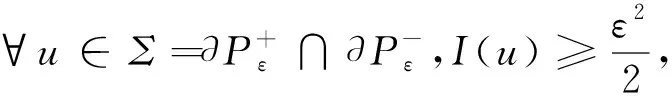
由引理10, 有

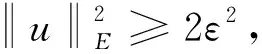
因此, 对足够小的ε,

则

下面应用引理8去证明本文的结论。 我们只需再验证引理8的2)和3)。

令ρ=min{‖tv1+(1-t)v2‖2:0≤t≤1}>0, 则‖u‖2≥ρR,∀u∈φ0(∂0Δ),且由引理10可知,对任意足够大的R,φ0(∂0Δ)∩M=∅, 满足了引理8的式2)。 由假设f3), 有F(t)≥C1|t|μ,∀t∈R。∀u∈φ0(∂0Δ), 由引理1,

4.2 无穷多变号解的存在性

假设G:X→X是一个等距对合, 即G2=id,且∀x,y∈X,d(Gx,Gy)=d(x,y)。 我们假设J在X上是G-不变的, 即对任意x∈X, 有J(Gx)=J(x)。也设Q=GP。 若∀x∈F, 有Gx=F, 则X的子集F叫做对称的。用γ(F)代表X(〗0}中的闭对称子集F的亏格。

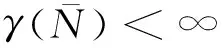
2)η∘G=G∘η;

3)η|Jc-2ε=id;

4)η(Jc+ε(N∪W))⊂Jc-ε。

则P被称为对J来说是G-可容许的在水平c的不变集。

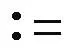
|x|≤1}→X满足:

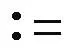
2)φn(∂Bn)∩M=∅;

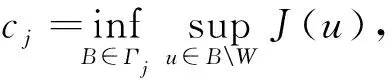
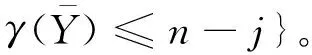
且

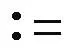
Gφ(t),φ(0)∈M且φ|∂Bn=φn|∂Bn},

则∀j≥2,cj≥c*,KcjW≠∅,且当j→∞时,cj→∞。

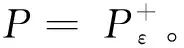
引理13存在ε0>0,使得∀0<ε<ε′<ε0, 存在一个连续映射σ:[0,1]×E→E满足:

1) ∀u∈E,σ(0,u)=u;

2) ∀t∈[0,1],u∉I-1[c-ε′,c+ε′],σ(t,u)=u;

3) ∀(t,u)∈[0,1]×E,σ(t,-u)=-σ(t,u);

4)σ(1,Ic+ε(N∪W))⊂Ic-ε;

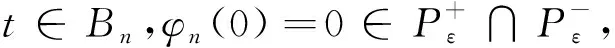
再由引理11, 当Rn足够大、且ε足够小时,

这满足了引理12的3)。 选择固定的Rn, 定义