面向大规模MIMO 的分块空间调制技术研究*

杨 晶，刘 云，吴 霆，梁奕念，呼 增,5＊

（1.电信科学技术第四研究所有限公司，陕西 西安 710061；2.广东金融学院，广东 广州 510521；3.仲恺农业工程学院，广东 广州 510225；4.华南理工大学，广东 广州 510641；5.广东省短距离无线探测与通信重点实验室，广东 广州 510640）

0 引言

随着越来越多的通信设备配备了多个收发天线，多输入多输出（Multiple-Input Multiple-Output，MIMO）传输技术逐步成为下一代无线通信网络的核心技术之一。在MIMO 系统中通过多天线共同发送调制符号，在贝尔实验室空时分层（Bell Laboratories Layered Space Time，BLAST）模式下可以在不增加带宽的情况下实现信道容量的大幅提升，同时可以有效降低系统的误比特率（Bit Error Rate，BER）[1-2]。然而，在MIMO 系统中多个发送天线同时发送调制符号，会引起严重的信道间的干扰问题，也对不同天线之间的信号同步提出了更高的要求。为了解决上述问题，空间调制（Spatial Modulation，SM）在每个发送时隙中只激活一个发送天线发送调制符号，可以有效解决发送天线间的干扰和信号同步问题，同时获得高于传统单天线系统的频谱效率[3]。

在空间调制系统中，信息比特通过两种方式来发送，即激活天线的索引序号模式组合和激活天线发送的调制符号。在本文中，通过序号模式组合发送的信息比特称为序号比特，通过激活天线发送的调制符号承载的信息比特称为符号比特。与MIMO系统比较，空间调制技术有较大的频谱效率损失，为了提升系统频谱效率，广义空间调制（Generalized SM，GSM）在每个时隙的发送方案中激活多个发送天线发送调制符号，并使用发送天线的激活天线模式组合来发送信息比特[4-5]。在广义空间调制中选择多个发送天线来发送传统调制符号，即每个时隙可以发送多个调制符号，可以获得更优的频谱效率。

针对广义空间调制接收端的研究主要集中在实现低复杂度的信号解调算法，即通过对接收信号进行预处理实现低复杂度的解调计算。对接收信号做最小均方误差（Minimum Mean Square Error，MMSE）均衡处理后，基于接收符号矢量计算每个发送天线对应的对数似然比（Log-Likelihood Ratio，LLR）值，可以获得发送天线对应的激活模式组合；然后计算激活天线发送的调制符号[6-8]。在球形译码算法中，通过设置半径可以有效缩小每个天线发送符号的搜索空间，在MIMO 系统中，若具有较多发送天线，可以大幅降低计算复杂度[7-10]。为了简化球形译码算法中每一个计算阶段的计算并保留搜索空间的半径时的复杂度，基于序贯蒙特卡洛（Sequential Monte Carlo，SMC）的检测算法在每一个发送天线对应符号的计算中保留固定个数的最有可能的发送调制符号，用于下一个天线对应的符号的计算[10]。

在广义空间调制中，激活天线模式组合的总数是发送天线数量和激活天线数量的组合数，其数值随着发送天线数量和激活天线数量的增长而快速增长，导致在大规模MIMO 系统中广义空间的调制与解调的计算复杂度变得过高，使得广义空间调制无法应用于大规模MIMO 系统中。为了简化在大规模MIMO 系统中广义空间调制的计算复杂度，本文提出一种基于分块模式实现的广义空间调制（Subblock based GSM，S-GSM），通过在每个子块中实现相互独立的广义空间调制，并由每个子块的激活天线模式组合构成完整的发送天线激活模式组合，从而实现发送端的高效调制和接收端的低复杂度解调。

1 系统模型

本文提出的分块空间调制技术基于一个具有NT个发送天线和NR个接收天线的MIMO 系统，其基本的收发系统框架如图1 所示。根据分块空间调制的基本原理，首先将NT个发送天线分成G个相互独立的子块，其中每个子块包含nt=NT/G个发送天线。在S-GSM 中，最简单的实现方式是每个子块执行相互独立的空间调制，但这种方法会降低空间调制系统中的激活天线模式组合的利用率，导致频谱效率损失。为了提升系统频谱效率，本文提出一种用于S-GSM 的联合序号调制方法，将不同子块的激活天线模式组合构成一个完整的激活天线模式组合，提高序号调制中的激活天线模式组合的利用率和频谱效率。定义每个子块为基本序号调制的单位，在每个子块的nt个发送天线中选择K个发送天线发送调制符号，则每个子块的基本序号调制集合为T(nt,K)，其中，1 ≤K＜nt为每个子块的激活天线数量，激活模式天线组合的数量为β=(nt,K)，C(·)表示组合数计算。表1 给出了参数nt=4，K=2 时的基本序号调制集合中的子块激活天线模式组合，其中子块激活天线模式组合的数量β=6。

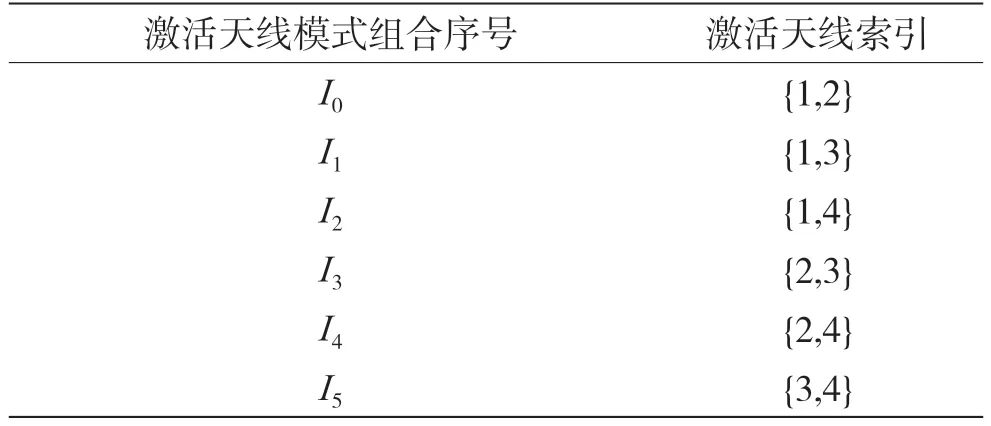
表1 参数为nt=4，K=2 时的基本序号调制集合

图1 S-GSM 系统发射端的联合序号调制模型

在S-GSM 中，完整的激活天线模式组合通过每个子块的激活天线模式组合得到，定义第g个子块得到的激活天线模式组合为，则由G个子块组成的完整的激活天线模式组合可以表示为：

式中：ig为第g个子块的激活天线模式组合在基本序号调制集合T(nt,K)中的序号。在序号调制中，将当前时隙的输入信息比特b分为两个部分，其中第1 部分为序号比特b1，第2 部分为符号比特b2，且有b=b1+b2。在序号调制中，选择激活天线模式组合中的2 的幂次方个用于序号调制，则每个时隙可以发送b1=log2βG」个序号比特。

在发送端的序号调制中，需要将输入的序号比特进行序号调制，得到每一个子块的激活天线模式组合。本文提出一种基于多项式计算的方法，通过计算输入的序号比特b1得到一个十进制数值d0，然后基于多项式的系数计算得到每个子块的激活天线模式组合。根据十进制数值d0和参数β可得序号调制多项式为：

式中：aG=1，ag=βG-g为第g个子块对应的多项式系数。根据多项式的系数，从第1 个子块对应的激活天线模式组合的序号开始计算，可得：

此时，更新后的十进制数值为：

第g个子块对应的激活天线模式组合的序号ig和十进制数值的更新计算过程为：

完成所有子块的激活天线模式组合的序号计算后，可得完整的激活天线模式组合，其完整表达式如式（1）所示。

在S-GSM 中，每个子块均有K个激活天线发送调制符号，则总共可以发送b2=Nklog2M个符号比特，其中Nk=GK为每个时隙发送的调制符号数量。基于b2个符号比特可得调制符号矩阵为S=(s1,s2,…,sG)，其中sg为第g个子块对应的K×1的非零调制符号矢量。根据得到的第g个子块的激活天线模式组合映射得到对应的发送符号矢量为。将得到的G个子块的发送符号矢量连接起来，得到完整的发送符号矢量为：

对比传统分组空间调制方案，联合序号调制方法将各子块的序号调制联合起来进行处理，可以获得更好的序号模式组合利用率，在每个时隙的传输中可以发送更多的序号比特。在S-GSM 系统中定义系统信噪比为ρ=Eb/N0，其中，Eb=Nk/b为每比特平均能量。

在接收端得到的NR维的接收信号矢量为：

式中：y为NR×1 的接收信号矢量；H为NR×NT信道矩阵；w为NR×1 的高斯白噪声矢量，其中的元素均值为0，方差为N0；i1,i2,…,iNk表示激活天线在信道矩阵H中对应的列的索引。基于最大似然（Maximum Likelihood，ML）准则的接收机检测算法可以获得最优的系统BER 性能，但其检测过程需要遍历所有可能的发送符号矢量，其检测过程可表示为：

式中：S表示M阶的传统QAM/PSK 星座图。基于ML 准则的检测算法的计算复杂度随着星座图的阶数和激活天线模式的组合数量的增长呈指数增长，其计算复杂度可表示为(2NRNT+2NR-MNkNC)。当S-GSM 中发送天线数据较多时，基于ML 的检测算法的计算复杂度非常高，无法应用于实际的便携式设备中，因此低复杂度的检测算法成为该领域的研究热点。

2 改进的分块球形检测算法

在基于分块模式的空间调制系统中，每个子块均有固定数量的发送天线被激活发送调制符号，因此在解调计算中需要对每个子块的激活天线模式组合进行判决。首先对接收信号矢量进行预处理，可得：

式中：(HN)H=(HHH)-1/2为接收信号预处理矩阵，为经过预处理后得到的NT×1 的接收信号矢量。对预处理后得到的等效信道矩阵进行QR 分解处理后可得：

式中：矩阵是一个NT×NT的酉矩阵，矩阵是一个NT×NT的上三角矩阵。左乘矩阵的共轭，得到处理后的接收信号矢量为：

从式（11）中的信号模型知，分块球形译码算法从接收信号的最后一个符号开始计算，在每计算得到一个子块可能的发送符号矢量时，做一次激活天线模式组合的合法性判决，保留合法的发送符号矢量用于下一个子块的计算。基于分块方式的改进的球形译码算法的计算步骤如下：

（1）计算第G个子块中的第t个发送天线对应的调制符号，其中(G-1)nt≤t≤Gnt，基于符号集合{S,0}计算到达第t个发送天线时的发送符号矢量的度量值为：

式中：rt=(0,…,rt,t,…,rt,NT)为由矩阵R的第t行元素组成的行矢量，xt=(0,…,xt,…,)T为到达第t个发送天线时的发送符号矢量。基于式（12）中计算得到的度量值，保留最多θ个具有较优度量值的发送符号矢量用于下一步的计算，其对应的第t个天线到第NT个天线对应的符号可以表示为其中i=1,2,…,θ。

（2）基于上一步中得到的θ个具有较优度量值的发送符号矢量，第t-1 个发送天线对应的发送符号矢量集合为：

式中：xt-1∈{S,0}，i=1,2,…,θ。在构建发送符号矢量的过程中，需要考虑每个子块的基本序号调制集合中的模式组合中激活天线的数量约束。当中非零符号矢量等于激活天线数量时，在接下来的计算中，xt-1=0 对应非激活天线，可知不同得到的发送符号矢量是不同的。基于第t-1 个发送天线对应的矢量rt-1，式（13）中的发送符号矢量的度量值可以基于式（12）计算，并保留最多θ个符号矢量用于下一个天线对应符号的计算。

（3）当计算过程完成一个子块后，保留最多θ个符号矢量用于下一个子块的计算。重复步骤（1）～（2）直到下一个子块对应的符号计算完成，并最多保留θ个发送符号矢量。注意在步骤（2）中的激活天线数量的约束仅需要考虑当前计算的子块。

（4）当计算过程到达第一个天线对应的符号后，则发送符号矢量的估计为：

在分块球形译码计算中，每个子块的计算均按照基本序号调制集合中的激活模式组合对非零调制符号的数量和位置进行约束，可避免最终估计结果中出现非法激活模式组合。

在得到最终的符号矢量估计结果后，基于式（2）计算得到激活天线模式组合对应的十进制数字，转换为二进制后得到序号比特的估计，然后根据激活天线发送的调制符号矢量得到符号比特的估计。分块球形译码检测算法的计算复杂度主要包括信号预处理和信号检测部分，则其计算过程中的主要浮点运算的计算复杂度为：

对比基于ML 准则的检测算法，可知基于子块的球形译码算法通过计算每个天线可能发送的符号的方式有效降低了计算复杂度，同时可以通过控制计算过程中到达每个天线时保留的符号矢量数量实现计算复杂度和系统BER 性能之间的最佳折中，可以满足不同的应用场景对系统性能和计算复杂度的要求。

3 仿真结果与分析

本节分析当[NT×NR]=[4×4,8×8,12×12]时，接收端分别采用ML 准则检测算法和分块球形译码检测算法进行解调计算的复杂度和误比特性能。在传统GSM 系统中基于整个发送天线执行序号调制，其序号模式组合数量随着发送天线数量和空间调制参数快速增长，因此在仿真中只对比了NT={4,8}时GSM 的误比特性能。在S-GSM 系统中，当NT=4 时，每个子块的发送天线数量为nt=2，在NT={8,16}时，设置每个子块中的发送天线数量为nt=4，其中每个子块的激活天线数量为K=nt/2。GSM 系统中选择NT/2 个天线发送调制符号。假设接收端通过信道估计可以获得准确的信道响应信息，而发送端只能通过接收端的反馈信息得到信道状态信息。在仿真图中，分块球形译码算法使用SD 来标记。

在S-GSM 系统中，联合序号调制基于每个子块的基本序号调制集合，将输入的序号比特通过多项式算法映射得到激活天线模式组合，在发送端和接收端仅需要保存基本序号调制集合，而GSM 系统需要在收发两端保存完整的查找表。表2 给出了不同MIMO 配置中收发两端需要保存的查找表集合的对比数据。从表2 中的数据可以看到，在S-GSM系统中不同的MIMO 配置可以使用相同的基本序号调制集合，因此，在大规模MIMO 系统中使用该系统可以有效降低发送端的调制计算复杂度。

表2 不同MIMO 配置中需要保存的查找表集合数量

图2 比较了4×4 和8×8 MIMO 配置下S-GSM和传统GSM 在使用最优ML 接收检测算法时的BER 性能比较，其中调制符号使用4QAM。在4×4的MIMO 配置下，S-GSM 和GSM 具有相同的激活天线模式组合，因此取得了一致的BER 性能。在8×8 的MIMO 配置下，S-GSM 获得了更优的BER性能，由于每个子块中限制配置2 个激活天线，使得S-GSM 系统的激活天线模式组合数量少于GSM 系统，导致较小的频谱效率损失，但在大规模MIMO 系统中S-GSM 可以有效降低系统实现的复杂度，其优势随着MIMO 系统中发送天线数量的增长变得更加明显，因此具有较大的工程应用价值。分块球形译码算法在计算过程中保留足够符号矢量时可以取得与最优ML接收算法几乎一致的BER性能，表明分块球形译码算法可以有效降低系统的解调计算复杂度，并且不会引入较大的BER 性能损失。

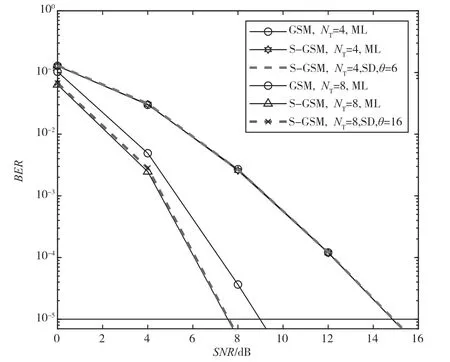
图2 不同MIMO 配置中S-GSM 和GSM 的BER 性能比较

图3 比较了在8×8 和12×12 的MIMO 配置下，S-GSM 系统使用改进的分块球形译码算法时保留不同数量的符号矢量时的BER 性能比较，其中8×8 MIMO 使用8QAM 星座图，12×12 MIMO 中使用4QAM 星座图。从图3 中可知，分块球形译码算法中每步计算保留的发送符号矢量数量θ对系统的BER 性能具有很大的影响，当保留的数量增长时，系统BER 性能快速改善并获得接近最优的ML 检测算法的BER 性能，但增长到一定数量后系统BER性能不再有明显改善，因此，在分块球形译码算法中保留适当数量的符号矢量可以获得接近最优的BER 性能。

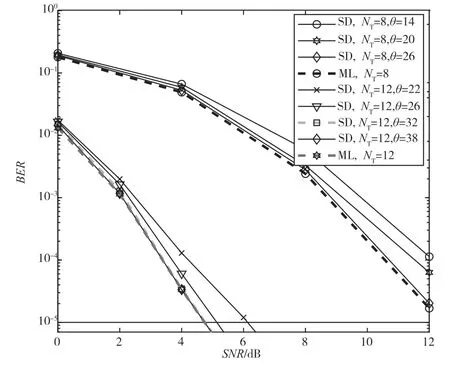
图3 S-GSM 中分块球形译码算法在不同θ 时的BER 性能比较

4 结语

本文面向大规模MIMO 系统提出了一种新颖的分块方式的空间调制方法，通过将发送天线进行分组并使用联合序号调制方式得到发送符号矢量。由于每个发送天线子块具有较小的维度，因此基本序号调制集合中的激活模式组合数量远少于传统GSM系统，可以有效降低系统发送端的调制过程的计算复杂度。在接收端，本文提出了一种改进的分块球形译码检测算法，在每个子块的计算中检查激活天线模式组合的合法性，确保最终得到的估计结果具有合法的激活天线模式组合。仿真结果表明，本文提出的分块球形译码检测算法可以在大幅降低解调计算复杂度的同时，取得接近最优的误比特性能，因此在大规模MIMO 场景的便携式设备等应用中具有重要的价值和意义。