一种基于自适应Kriging集成模型的结构可靠性分析方法

高进 崔海冰 樊涛 李昂 杜尊峰

摘要：基于Kriging模型的复杂结构可靠性分析结果高度依赖于Kriging模型的拟合精度，在构建Kriging模型的过程中，不同相关函数和回归函数的选择均会影响模型精度。为解决模型的不确定性对可靠性分析结果的影响，同时兼顾计算效率和精度，基于Kriging模型和蒙特卡罗模拟（MCS）方法，提出了一种结合自适应集成策略和主动学习函数的结构可靠度计算方法。该方法考虑Kriging模型的建模不确定性，将多种Kriging模型组合，构建了一种综合考虑样本点贡献和样本点距离的主动学习函数，通过主动学习函数迭代更新集成Kriging模型直至满足收敛条件，最后通过构建的集成Kriging模型和MCS方法进行结构可靠性分析。数值算例和工程算例结果验证了所提方法的有效性，该方法与其他主要方法相比稳健性更好，在保证计算精度的同时，计算效率更高。

关键词：结构可靠性；自适应集成策略；Kriging模型；主动学习函数

中图分类号：TH122

DOI：10.3969/j.issn.1004132X.2024.01.008

A Structural Reliability Calculation Method Based on Adaptive Kriging

Ensemble Model

GAO Jin1，2 CUI Haibing1，2 FAN Tao3 LI Ang3 DU Zunfeng3

1.Weichai Power Company Limited，Weifang，Shandong，261061

2.State Key Laboratory of Engine Reliability，Weifang，Shandong，261061

3.School of Civil Engineering，Tianjin University，Tianjin，300354

Abstract： The reliability analysis results of complex structures based on the Kriging model were highly dependent on the fitting accuracy of the Kriging model. In the constructing processes of the Kriging model， the selection of different correlation and regression functions affected the accuracy of the model. In order to solve the impacts of model uncertainty on the reliability analysis results， while considering computational efficiency and accuracy， based on the Kriging model and Monte Carlo simulation（MCS） method， a structural reliability calculation method combining adaptive ensemble strategy and active learning function was proposed. Considering the modeling uncertainty of Kriging models， combined with multiple Kriging models， this methed constructed an active learning function that comprehensively considered sample point contribution and sample point distance. The ensemble Kriging model was iteratively updated through the active learning function until the convergence conditions were satisfied. Finally the structural reliability analysis was carried out by the constructed ensemble Kriging model and MCS method. The validity of the proposed method was verified by numerical and engineering examples， and the results show that the proposed method is more robust than other major methods， and the computational efficiency is higher while ensuring the computational accuracy.

Key words： structural reliability； adaptive ensemble strategy； Kriging model； active learning function

0 引言

綜合考虑多源不确定性的机械结构可靠性分析在实际工程中具有重要意义，但机械结构的功能函数多为隐式函数，且计算往往涉及大量有限元仿真计算，传统方法如蒙特卡罗模拟（MCS）方法、一阶可靠性方法及二阶可靠性方法等已无法满足实际工程需求［1］，因此，利用代理模型来替代结构的实际功能函数进行结构可靠性分析已经成为可靠性研究的重要分支和关键技术［2］。其中，Kriging模型具有估计方差小且无偏，适用于高度非线性、高维度的复杂结构系统，在可靠性领域备受关注［3］。近年来，为提高基于Kriging模型的可靠性分析方法的计算精度和计算效率，相关研究主要集中在以下三个方向：

一是通过自适应学习函数更新代理模型。目前，BICHON等［4］提出的预期可行性学习函数（expected feasibility function，EFF）和ECHARD等［5］提出的考虑样本点被错误估计概率的自适应U函数应用最为广泛，ZHENG等［6］考虑样本点对失效概率的贡献，对U函数进行了改进，进一步提高了Kriging模型的收敛速度。SUN等［7］提出的最小改进函数（least improvement function，LIF）提高了Kriging模型的拟合精度。二是提高Kriging模型拟合精度。HAN等［8-9］考虑样本点的梯度信息，构建了梯度增强Kriging模型（gradient-enhanced Kriging，GE-Kriging）。SCHOBI等［10-11］将多项式混沌展开（polynomial chaos expansion，PCE）与Kriging模型相结合，即将PCE的最优截断集合作为Kriging模型的回归函数部分，提出了多项式混沌Kriging模型（polynomial-chaos-based Kriging，PC-Kriging），并基于PC-Kriging模型提出了一种新的可靠性分析方法。三是改进抽样方法并与Kriging模型相结合进行可靠性分析。ZHANG等［12］和BARKHORI等［13］分别提出了将Kriging模型与子集模拟抽样（subset simulation，SS）和重要性抽样（importance sampling，IS）相结合的可靠性计算方法。史朝印等［14］基于Kriging模型和交叉熵重要性抽样法提出了一种新的可靠性分析方法，该方法通过Kriging模型协助混合高斯模型参数更新，引入重要性抽样思想，缩小了MCS仿真样本的规模，并通过算例验证了其优越性。

综上所述，已有的相关研究所提出的基于代理模型的可靠性分析方法都有着较高的准确度和效率，但均是在单一Kriging模型下展开研究，忽略了Kriging建模过程中相关函数与回归函数的选择不确定性问题，而这一问题可能会导致Kriging模型预测性能不佳［15］，另一方面，由于每种代理模型各有优劣，而在面对隐式功能函数时，在设计前难以了解其特性，如何选取合适的代理模型是一个难题。CHENG等［16］提出了一種基于PCE、SVM、Kriging的集成代理模型可靠性分析方法，但该方法在更新训练集时，需额外计算预测点的统计信息，容易引起集成误差，可能导致集成代理模型在部分区域拟合不佳。李宁等［17］提出了基于自适应集成学习代理模型（Kriging模型与PC-Kriging模型）的结构可靠性分析方法，提高了可靠性分析的准确性与效率，但该方法未考虑Kriging模型的相关函数的选择对拟合结果的影响。在实际问题中，由于功能函数往往非常复杂且为隐式，缺乏足够的先验信息，一般很难选择最优的Kriging模型。对此，本文基于自适应集成策略，对不同回归函数和相关函数下的Kriging模型进行加权集成，解决了难以选择最优Kriging模型的问题，结合所提出的改进学习函数，提出了一种基于自适应Kriging集成模型的结构可靠性分析方法，并通过算例予以验证。

1 Kriging模型

1.1 Kriging模型基本理论

Kriging模型是一种半参数的高效插值方法，是根据协方差函数对随机过程进行建模和预测的算法，它由两部分组成：随机部分和多项式回归。对于任意已知的m个n维样本点（X1，X2，…，Xm），其对应的真实响应值为（G（X1），G（X2），…，G（Xm）），则对任意输入向量X与其Kriging模型的预测值G（X）关系可表示为

G（X）=（g（X））Tβ+z（X）（1）

其中，（g（X））Tβ为Kriging模型的回归函数，表示高斯过程的均值；g（X）为模型的基函数；β为g（X）对应的回归系数；z（X）表示均值为0的高斯随机过程，其方差为σ2，协方差可表示为

Cov［z（Xi），z（Xj）］=σ2R（Xi，Xj，θ）（2）

式中，R（Xi，Xj，θ）表示z（Xi）和z（Xj）的相关函数；θ表示R（Xi，Xj，θ）的相关参数，可通过最大似然估计求出。

1.2 Kriging模型的相关函数和回归函数

Kriging模型建模过程中存在多种相关函数选择不确定性问题，相关函数的选择应考虑功能函数性质和变量的分布特点。常用相关函数R（Xi，Xj，θ）形式有指数函数、高斯函数、三次函数、Matérn函数［18］等，本文选择指数函数、高斯函数、Matérn函数三类相关函数构建集成代理模型，它们具体的表达式如表1所示。

回归函数g（X）Tβ反映了Kriging代理模型的预测趋势，常见的回归函数主要有常量回归、线性回归、2阶回归等［18］，尽管（g（X））Tβ的具体形式对Kriging模型的拟合精度影响不大［19］，但文献［10］将PCE作为Kriging模型的一种回归函数，构建的PC-Kriging模型具有较好的拟合性能。因此本文选择PCE回归函数和常量回归函数构建集成代理模型。PCE通过多项式展开，对函数的近似拟合输出可表示为

式中，ψa（X）为多变量标准正交多项式，其系数为ya；A为多项式阶数。

利用PCE替代Kriging模型的基函数g（X）得到对应的PC-Kriging模型如下式所示［20］：

综上，本文对PCE回归和常量回归两类Kriging模型分别构建其在指数函数、高斯函数、Matérn3/2函数以及Matérn5/2函数四种相关函数下的代理模型，共计8种Kriging模型（表2），结合自适应集成策略构建集成代理模型。

2 基于自适应Kriging组合模型的可靠性分析方法

2.1 自适应集成策略

集成代理模型的基本思想是使用加权形式对多个代理模型进行聚合，以充分利用每个代理模型的预测能力，同时解决难以选择最佳代理模型的问题。集成代理模型有如下表达式：

式中，K为所使用的代理模型的个数，本文K=8；M（X）为集成代理模型对任意输入向量X的预测值；i（X）为第i个代理模型对任意输入向量X的预测值；wi为第i个代理模型的权重。

文献［21］提出了一种基于全局预测误差确定权重的启发式策略，表达式如下：

其中，εLi为第i个模型全局预测误差，为尽可能减少功能函数调用次数，选择全局留一交叉验证误差（leave-one-out，LOO）作为全局预测误差。α（α<1）、β（β<0）分别为控制单个代理模型相对重要性的两个参数，根据文献［21-22］分别取α=0.05，β=-1。

2.2 主动学习函数

主动学习函数是指在更新代理模型过程中，根据学习函数值将样本集进行排序，并筛选合适的样本点添加到训练集中，以提高代理模型的预测精度。由于在实际工程应用中，功能函数的计算涉及到大量的有限元分析计算，计算时间长，因此，在构建代理模型时，需要在保证计算精度的情况下尽可能减少训练集的样本点个数，本文基于IEGO（improved efficient global optimization）学习函数［19］，提出了一种新的主动学习函数。

IEGO学习函数基于JONES等［23］首次提出的EGO学习函数，为使代理模型在极限状态附近拟合精度更高，文献［19］对EGO学习函数中的期望值定义进行调整，使其选点策略更符合可靠度计算的要求。IEGO学习函数定义如下：

首先定义样本点X处对Kriging模型的改进程度为

式中，σ（X）为Kriging模型的预测方差；Φ（·）、φ（·）分别表示标准正态分布的累积分布函数和概率密度函数。

则下一次待添加到实验设计（DoE）的最佳样本点为所有样本点中期望值最大所对应的点Xbest。

但IEGO学习函数只优先考虑了极限状态方程附近的拟合，未考虑样本点的距离对拟合效率的影响，事实上，在选择最佳新样本点的同时，学习函数必须考虑样本聚类的潜在风险，以避免构建代理模型时出现过拟合，因此，采用以下距离准则来保证待添加到DoE的最佳样本点远离现有的样本点。距离函数定义为

式中，Xi为已有的训练集中样本点；dm（X）为待添加样本点与已有样本点的最近距离;dmin为已有样本点之间的最小距离。

本文在IEGO学习函数的基础上，提出了一种考虑样本点聚集的改进学习函数IE（X），其表达式如下：

基于式（11），选择候选样本点中IE（X）值最大的样本点作为新增样本点加入到实验设计中，重新生成集成Kriging模型，直至输出的失效概率达到稳定状态，满足下式所示［24］的收敛条件，迭代终止：

2.3 可靠度计算流程

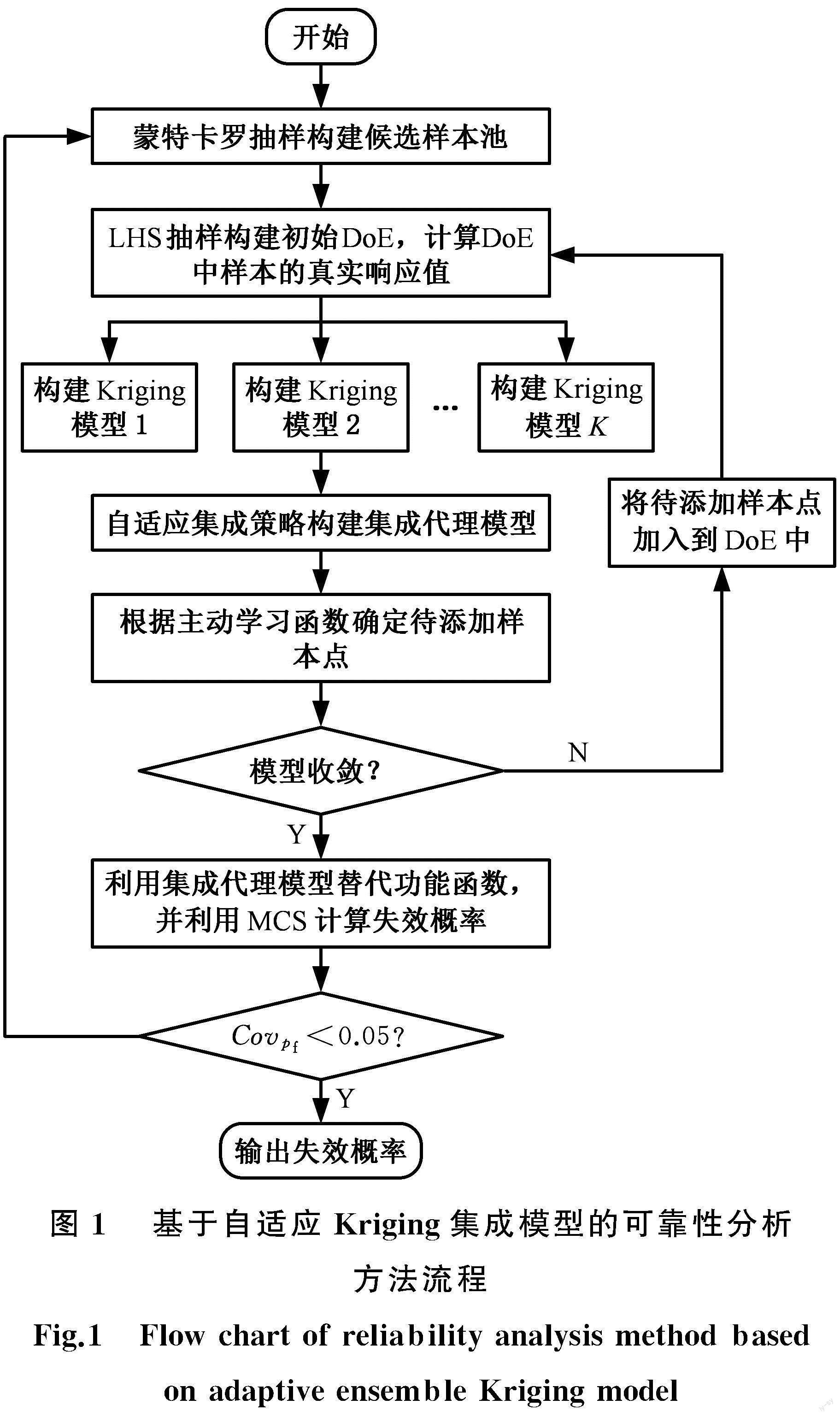
基于集成Kriging模型和蒙特卡罗抽样，结合本文提出的改进学习函数的可靠性分析方法主要流程如图1所示。

主要步骤如下：

（1）采用蒙特卡罗抽样构建候选样本池，根据随机变量的分布类型抽取Nmc个样本点作为样本池（X1，X2，…，XNmc）。

（2）采用拉丁超立方抽样法（Latin hypercube sampling，LHS）生成DoE中的初始样本点（X1，X2，…，Xn），并计算其真实功能函数响应值（G（X1），G（X2），…，G（Xn））。

（3）根据DoE中的初始样本点及真实响应值初步构建K种Kriging模型，并根据式（5）、式（6）计算每个代理模型集成權重，构建集成Kriging模型，最后利用集成Kriging模型去计算候选样本池中所有点的预测均值和标准差。

（4）根据步骤（3）中的结果计算式（11）中的IE（X）。

（5）根据学习函数的停止准则判断是否需要更新集成Kriging模型，若不满足停止准则，则根据本文提出的学习函数和步骤（4）的计算结果选择IE（X）最大值所对应的样本点作为新的样本点加入DoE中，跳转到步骤（3），否则，执行下一步。

（6）基于集成Kriging模型的预测均值，采用MCS计算失效概率f和变异系数CovPf，当CovPf≤0.05时，输出f，否则，更新样本池Nmc，执行步骤（1）。其中

3 算例验证

为了验证本文方法的有效性，现通过三个算例进行验证，每一个算例均使用本文方法和常用的AK-MCS-U［5］、AK-MCS-EFF［4］、AK-MCS-IEGO［19］、MCS等方法进行计算比较，验证本文所提方法在计算可靠度方面的有效性和正确性，需要说明的是，其他方法的Kriging模型的相关函数采用高斯函数，回归函数采用常量回归。

3.1 数值算例

3.1.1 算例1：四分支串联系统

本算例功能函数如下［5］：

式中，x1、x2相互独立且均服从正态分布，x1～N（0，1），x2～N（0，1）;k=6，7。

首先根据变量分布函数和蒙特卡罗抽样函数构建候选样本池，再利用LHS抽样获得初始样本，并根据式（15）获得真实响应值，拟合初始的Kriging模型，然后根据学习函数不断更新集成Kriging模型直至收敛，输出求解的失效概率Pf，并以MCS方法的结果PMCf（视作精确值）作为参照，利用下式计算各个结果的相对误差：

运算结果如表3所示，可以看出本文所提出的方法与AK-MCS-U、AK-MCS-EFF等主要方法相比，在保证计算准确度的同时，能够显著减少系统模型下对其功能函数的调用次数。

图2展示了AK-MCS-U、AK-MCS-EFF、AK-MCS-IEGO和本文所提方法所对应的四类学习函数分别在k=6和k=7时最佳样本点分布。结合表3可以看出，虽然U函数在极限状态附近的拟合效果较好，求解精度较高，但由于U函数的停止准则过于严格，样本点出现了大量的局部聚集，从而导致Kriging模型出现过拟合，增加计算成本，而EFF函数虽然调用功能函数次数最少，样本点分布也较合理，但计算精度较差，这是因为EFF函数在计算时容易出现提前收敛［25］，在k=7时，误差甚至达到了5.05%，不具备参考性。IEGO函数在极限状态附近拟合效果较好，但是在k=6，k=7时均出现了样本点局部聚集的情况，增加了计算成本，这也导致了虽然该方法计算精度与本文方法相近，但计算效率均低于本文方法计算效率。本文方法在保证最佳样本点处在极限状态附近的基础上，分布比IEGO函数更加均匀合理，未出现样本点局部聚集的情况，计算效率更高，说明了本文提出的考虑样本点距离的改进学习函数的有效性。

图3展示了k=6时不同Kriging模型的权重系数随模型迭代次数的变化趋势，可以看出PC-Kriging模型的权重系数整体上高于常量回归Kriging模型权重系数，Kriging模型5权重最高，说明了PC-Kriging模型比常规Kriging模型在拟合精度上具有一定的优势，在具有相同回归函数的Kriging模型中，采用Matérn5/2函数作为相关函数的权重较高，采用指数函数作为相关函数的权重较低，说明在此案例中，采用Matérn5/2函数作为相关函数的Kriging模型具有较好的拟合效果。

3.1.2 算例2：非线性振动系统

6维随机非线性振动系统如图4所示［8］，功能函数如下：

其中，c1、c2表示系统中两个连接弹簧刚度；M表示小车质量；R表示位移阈值；F1、t1分别为系统所受载荷幅值和时间。随机变量分布如表4所示。

根据变量（c1，c2，M，R，t1，F1）的分布函数生成候选样本池，然后利用LHS抽样在样本池中抽取12个样本点作为初始样本点进行迭代计算，同时，为了说明本文所提方法的穩定性，分别对AK-MCS-U、AK-MCS-EFF、AK-MCS-IEGO、AK-SS方法和本文所提方法进行30次计算，30次计算结果的平均值如表5所示，30次计算结果的失效概率箱型图见图5。

可以看出，五种方法的失效概率均在一定范围内波动，这是由抽样的随机性所导致的，同时，五种方法中，AK-MCS-U的波动最小，精度最高，最接近MCS的结果，但结合表4可以看出，该方法所添加的样本点最多，说明该方法虽然精度较高，但效率较低，而AK-MCS-EFF虽然效率较高，但是精度较低，本文所提方法不但能保证精度高、效率高的要求，结果的稳定性也比较强，这说明了本文方法的有效性。

为了说明本文提出的集成模型具有较好的稳定性，现分别取本文的集成模型和表2的8种Kriging模型分别与本文提出的学习函数相结合，对该算例计算30次，失效概率和新增样本点个数结果如图6所示。可以看出，基于不同代理模型所得的失效概率和新增样本点个数均在一定范围内波动，但集成模型的概率波动较小。综合来看，本文的方法能在保证计算精度的前提下，使稳定性更高，且计算效率较高。

3.2 工程算例：某配气机构传动系统的频率可靠性分析

发动机配气机构是一种控制燃料气体进出气缸的装置，是内燃机重要组成部分之一。所设计的配气机构性能好坏会直接影响内燃机的各项性能指标［26］。当配气机构传动系统的固有频率与凸轮的激振频率差值不超过某一固定阈值时，该传动系统会以最大的振幅开始振动，从而引起机械和结构很大的变形和动应力，即共振失效。为此，以某型号发动机配气机构为对象，利用所提方法对其进行结构可靠性分析，并与其他主要方法进行对比，以验证所提方法的工程应用价值。

图7为一发动机配气机构系统简图。其中，mt、mv、ms分别为挺柱AD、气门BC和气门弹簧质量；I、θ分别为摇臂AB对转轴O的转动惯量和转动角度；a、b分别为挺柱、气门到摇臂中心的距离；ks、kt分别为阀簧刚度和简化后挺柱的刚度，取kt=0；c一般为阻尼系数，由模态理论可知，阻尼系数对系统的固有频率影响可忽略不计，此处不予考虑。各随机变量的分布信息如表6所示。根据文献［26］所推导的配气系统振动可靠性的功能函数如下：

式中，ω为系统的固有频率；f为系统激振频率的统计量；γ为固定阈值，根据经验一般取系统固有频率均值的10%～15%。

与数值算例的求解流程类似，首先根据变量的分布函数生成候选样本池，然后利用LHS抽样抽取12个样本点作为初始样本点进行迭代计算，各方法计算结果如表7所示。结合表7可以看出，本案例中采用代理模型进行可靠性分析的精度都比较高，但本文提出的方法计算成本最低，说明与算例1、2相比，集成Kriging模型在拟合高维非线性函数时具有较大优势，仅需调用功能函数12+33次，极大地减小了计算量。

图8展示了本算例中不同Kriging模型的权重系数随模型迭代次数的变化趋势，可以看出PC-Kriging模型的权重系数整体上远远高于常量回归Kriging模型的权重系数。

结合图3可以看出，在拟合高维非线性函数时，结合PCE的Kriging模型相比于常量回归Kriging模型更有优势，采用常量回归函数和指数函数作为相关函数的Kriging模型精度较低，说明此类模型对高维非线性函数的拟合效果不佳。

为了进一步说明本文提出的集成模型在解决实际问题时具有较高的稳定性，现分别使用本文的集成模型和8种Kriging模型对该算例计算30次，其结果如图9所示。可以看出集成模型的计算次数和计算结果的波动均最小，说明集成模型的稳定性较好，与单一Kriging模型相比，集成模型稳定性和精度均有一定的提高。

4 结论

本文提出了一种基于集成Kriging模型与改进主动学习函数相结合的可靠性分析方法，并利用2个数值算例和1个工程案例验证了本文所提方法的有效性和高效性，主要结论如下：

（1）基于自适应集成策略对不同回归函数和不同相关函数下的Kriging模型进行集成，与单一Kriging模型相比，集成模型具有更高的稳健性，在解决工程实际问题时，能通过构建更稳健的代理模型来计算可靠度，保证计算结果可靠。

（2）在IEGO学习函数的基础上所提出的改进学习函数，既能够使最佳样本点分布于极限状态面附近，保证Kriging模型在极限状态面附近的拟合精度，又综合考虑了样本点之间的距离对拟合精度和拟合效率的影响，使得样本点能均匀分布于极限状态面附近，避免了样本点出现局部聚集，从而导致选点浪费。

（3）数值和工程算例验证了集成Kriging模型在处理高维非线性函数时具有较大优势，能够在保证计算精度的条件下实现对问题的高效求解。

本文所提出的集成Kriging模型的权重是将全局留一交叉验证误差（LOO）作为全局预测误差来确定各个模型的权重，但LOO是一种高方差估计，可能会导致某些性能较差的模型获得较高的权重，影响集成Kriging模型的拟合性能，在未来研究中，可考虑制定更有效的权重策略，以进一步提高模型的稳健性和求解精度。

参考文献：

［1］ 查从燚，孙志礼，潘陈蓉等.面向结构可靠性分析的并行自适应加点策略［J］. 东北大学学报（自然科学版），2023，44（1）：76-81.

ZHA Congyi， SUN Zhili， PAN Chenrong， et al．Parallel Adaptive Sampling Strategy for Structural Reliability Analysis［J］. Journal of Northeastern University， 2023， 44（1）：76-81.

［2］ 李永华，梁校嘉，宫琦.基于双点加点策略的改进Kriging响应面可靠度计算方法［J］.中国机械工程， 2019， 30（17）：2051-2057.

LI Yonghua， LIANG Xiaojia， GONG Qi. Improved Kriging Response Surface Reliability Calculation Method Based on Two Point Addition Strategy［J］. China Mechanical Engineering， 2019， 30 （17）：2051-2057.

［3］ 周成寧. 随机和认知不确定性下基于代理模型的结构可靠性方法研究［D］. 成都：电子科技大学，2021.

ZHOU Chengning. A Research of Surrogate Based Model for Structural Reliability Method under Aleatory and Epistemic Uncertainties［D］. Chengdu：School of Mechanical and Electrical Engineering， 2021.

［4］ BICHON B J，ELDRED M S，SWILERL L P，et al． Efficient Gobal Reliability Analysis for Nonlinear Implicit Performance Functions［J］. AIAA Journal，2008，46（10）：2459-2468．

［5］ ECHARD B，GAYTON N，LEMAIRE M． AK-MCS：an Active Learning Reliability Method Combining Kriging and Monte Carlo Simulation［J］. Structural Safety，2011， 33（2）：145-154．

［6］ ZHENG P，MING W C，ZONG G，et al.A New Active Learning Method Based on the Learning Function U of the AK-MCS Reliability Analysis Method［J］. Engineering Structures， 2017， 148：185-194.

［7］ SUN Z，WANG J，LI R，et al. LIF：a New Kriging Based Learning Function and Its Application to Structural Reliability Analysis［J］. Reliability Engineering and System Safety， 2017， 157：152-165.

［8］ HAN Z H，ZIMMERMAN R， GORTZ S. Alternative co-Kriging Method for Variable-fidelity Surrogate Modeling［J］. AIAA Journal， 2012， 50（5）：1205-1210．

［9］ HAN Z H，Gortz S，ZIMMERMAN R．Improving Variable Fidelity Surrogate Modeling via Gradient-enhanced Kriging and a Generalized Hybrid Bridge Function［J］. Aerospace Science&Technology， 2013， 25（1）：177-189.

［10］ SCHOBI R，SUDRET B，WIART J. Polynomial-chaos Based Kriging［J］. International Journal for Uncertainty Quantifications， 2015， 5（2）：171-193.

［11］ SCHOBI R， SUDRET B， MARELLI S. Rare Event Estimation Using Polynomial-chaos Kriging［J］. ASCE-ASME Journal of Risk and Uncertainty in Engineering Systems， Part A：Civil Engineering， 2017，3（2）：4016002.

［12］ ZHANG J， XIAO M，GAO L． An Active Learning Reliability Method Combining Kriging Constructed with Exploration and Exploitation of Failure Region and Subset Simulation［J］. Reliability Engineering and System Safety， 2019， 188：90-102.

［13］ BARKHORI M， SHAYANFAR M A， BARKHORDARI M A， et al. Kriging Aided Crossentropy-based Adaptive Importance Sampling Using Gaussian Mixture［J］. Iranian Journal of Science and Technology， 2019， 43（1）：S81-S88．

［14］ 史朝印， 吕震宙， 李璐祎， 等.基于自适应Kriging代理模型的交叉熵重要抽样法［J］.航空学报，2019，41（1）：223123.

SHI Zhaoyin，LYU Zhenzhou，LI Luyi，et al. Cross-entropy Importance Sampling Method Based on Adaptive Kriging Model［J］. Acata Aeronautica et Astronautica Sinica， 2020， 41（1）：223123.

［15］ 万良琪， 欧阳林寒. 基于0-1规划模型筛选策略的Kriging组合模型及可靠性优化设计［J］.计算机集成制造系统，2022，28（7）：2162-2168.

WAN Liangqi，OUYANG Linhan. Kriging Ensemble Model Based on 0-1 Programming Model Selection strategy for Reliability-based Design Optimization［J］Computer Integrated Manufacturing Systems， 2022， 28（7）：2162-2168.

［16］ CHENG K， LU Z. Structural Reliability Analysis Based on Ensemble Learning of Surrogate Models［J］. Structural Safety，2020，83：101905.

［17］ 李宁，潘慧雨，李忠献.一种基于自适应集成学习代理模型的结构可靠性分析方法［J］.工程力学，2023，40（3）：27-35.

LI Ning， PAN Huiyu，LI Zhongxian. Structural Reliability Analysis Method Based on Adaptive Ensemble Learning Surrogate Model［J］.Engineering Mechanics， 2023， 40（3）：27-35.

［18］ 李大帅. 基于多保真度Kriging代理模型的结构可靠度分析方法［D］. 哈尔滨：哈尔滨工业大学，2021.

LI Dashuai. A Structural Reliability Analysis Method Based on Multi-fidelity Kriging Surrogate Model［D］Harbing：Harbin Institute of Technology， 2021.

［19］ 洪林雄， 李华聪， 彭凯， 等. 基于改进学习策略的Kriging模型结构可靠度算法［J］.西北工业大学学报，2020，38（2）：412-419.

HONG Linxiong， Li Huacong， Peng Kai， et al. Structural Reliability Algorithms of Kriging Model Based on Improved Learning Strategy［J］. Journal of Northwestern Polytechnical University，2020， 38（2）：412-419.

［20］ 彭新款. 基于PC-Kriging替代模型的移动模架结构可靠度分析［D］. 广州：华南理工大学， 2019.

PENG Xinkuan. Reliability Analysis of Movable Scaffolding System Structure Based on PC-Kriging Surrogate Model［D］.Guangzhou：South China University of Technology， 2019.

［21］ GOEL T， HAFTKA R T， SHYY W， et al. Ensemble of Surrogates［J］. Structural and Multidisciplinary Optimization， 2007， 33（3）：199-216.

［22］ ZHANG H L， ZHOU C C， ZHAO H D， et al. An Ensemble Model-based Method for Estimating Failure Probability Function with Application in Reliability Based Optimization［J］. Applied Mathematical Modelling， 2022， 108：445-468.

［23］ JONES D R， SCHONLAU M， WELCH W J．Efficient Global Optimization of Expensive Black-box Functions［J］. Journal of Global Optimization，1998， 13（4）：455-492.

［24］ 石灵健. 基于主动学习代理模型的结构可靠性分析方法研究［D］. 南京：东南大学， 2019.

SHI Lingjian. Research on Structural Reliability Analysis Based on Active Learning Surrogate Model［D］. Nanjing：Southeast University，2019.

［25］ 吳振光. 基于主动学习Kriging代理模型的结构可靠性算法研究［D］. 沈阳：东北大学， 2020.

WU Zhenguang. Efficient Structural Reliability Algorithms with the Active-learning Based Kriging Model［D］. Shenyang：Northeastern University， 2020.

［26］ 杨周，刘洋，张义民.发动机配气机构传动系统的频率可靠性分析［J］.振动.测试与诊断，2017，37（2）：284-287.

YANG Zhou，LIU Yang， ZHANG Yimin. Frequency Reliability Analysis for Transmission System in Engine Valve Train［J］. Journal of Vibration，Measurement & Diagnosis， 2017， 37（02）：284-287.