基于FY-3D卫星的微波与光学陆表温度融合研究*

刘勇洪 翁富忠 徐永明 韩秀珍 段四波 唐世浩 叶成志

1 中国气象局地球系统数值预报中心,北京 100081 2 灾害天气国家重点实验室,北京 100081 3 南京信息工程大学遥感与测绘工程学院,南京 210044 4 国家卫星气象中心,北京 100081 5 中国农业科学院农业资源与农业区划研究所,北京 100081 6 湖南省气象局,长沙 410118

提 要：目前还没有基于国产卫星的1 km分辨率的全天候陆表温度(LST)产品,FY-3D 卫星提供了中分辨率成像仪(MERSI)Ⅱ型1 km分辨率晴空LST产品与微波成像仪(MWRI)25 km全天候LST产品,因此可结合两者优势开展全天候1 km 分辨率LST的融合研究。基于地理加权回归(GWR)方法,选择海拔、FY-3D 归一化植被指数和归一化建筑指数等建立GWR模型对FY-3D/MWRI 25 km LST降尺度到1 km,并与MERSI 1 km LST进行融合;同时针对MWRI轨道间隙,利用前后1天融合后的云覆盖像元1 km LST进行补值,可以得到接近全天候下的1 km LST。基于以上融合算法,选择了中国区域多个典型日期FY-3D/MERSI和MWRI LST官网产品进行了融合试验,并利用公开发布的全天候1 km LST产品(TPDC LST)对FY-3D 1 km LST融合结果进行了评估。研究结果表明,基于GWR法的LST降尺度方法,可以有效避免传统微波LST降尺度方法中存在的“斑块”效应和局地温度偏低等问题;LST融合结果有值率从融合前的22.4%～36.9%可提高到融合后69.3%～80.7%,融合结果与TPDC LST的空间决定系数为0.503～0.787,均方根误差为3.6～5.8 K,其中晴空为2.6～4.9 K,云下为4.1～6.1 K;分析还表明目前官网产品FY-3D/MERSI和MWRI LST均存在缺值较多与精度偏低等问题,显示其存在较大改进潜力,这有利于进一步改进FY-3D LST融合质量。

引 言

陆表温度(LST)是研究全球与区域气候变化的重要参数(Li et al,2013;Yu et al,2018),特别是获取1 km空间分辨率的全天候LST已经成为相关研究和应用领域的迫切需求(Hijmans et al,2005;Fick and Hijmans,2017;Zhang et al,2020)。基于光学(可见光与热红外)遥感数据所获得的LST,虽然空间分辨率高(一般为1 km或优于1 km),反演精度较高(Wan,2008;权维俊等,2012;Liu et al,2015;Duan et al,2019),但是受限于晴空天气条件,存在大量的缺失像元或无效像元(Cornette and Shanks,1993),不能进行LST的全天候监测。不同于光学波段,微波可以穿透云层,提供了获取全天候LST的有效手段,但空间分辨率远低于光学反演得到的LST(一般为10～36 km),LST反演精度较低(McFarland et al,1990;Zhou et al,2015),且轨道间存在间隙,反演的LST空间不连续。因此,结合两者优势开展微波与光学LST的融合目前已成为全天候1 km分辨率LST研究热点(Duan et al,2017;Xu et al,2019;Yoo et al,2020;Zhang et al,2020;Tang et al,2022)。

目前在微波与光学LST融合研究中,采用的卫星数据仍以国外为主,其中微波主要采用AMSR-E(Advanced Microwave Scanning Radiometer for EOS)和AMSR-2(Advanced Microwave Scanning Radiometer 2)数据,光学主要为MODIS(Moderate-resolution Imaging Spectroradiometer)数据,而利用我国卫星开展全天候的1 km分辨率LST融合研究尚未见报道。风云三号气象卫星D星(FY-3D)是我国自主研制的最新一代极轨气象卫星,其上搭载的中分辨率成像光谱仪(MERSI-Ⅱ)是世界上首台能够获取全球 250 m分辨率红外分裂窗区资料的成像仪器,其中热红外分裂窗波段第24和第25波段与MODIS分裂窗波段光谱接近(蒋金雄等,2019;Tang et al,2021),已有研究表明FY-3D MERSI-Ⅱ具有与MODIS类似的LST产品反演精度(Wang et al,2019;Du et al,2021;Aveni and Blackett,2022);而FY-3D卫星携带的微波成像仪(MWRI)提供了5个观测频率波段(10.65、18.7、23.8、36.5和89.0 GHz)垂直极化和水平极化共10个可接收的亮温通道(朱瑜馨等,2021;王博等,2022;刘梅等,2022),由于FY-3D MERSI-Ⅱ与MWRI在过境时间上具有一致性,故利用FY-3D MERSI-Ⅱ反演的陆表温度(简称FY-3D/MERSI LST)与MWRI反演的LST(简称FY-3D/MWRI LST)开展全天候1 km分辨率LST融合研究,对于国产气象卫星在全球陆表生态环境监测与全球气候变化的应用具有重要意义。

在全天候1 km分辨率光学与微波LST融合研究中,最为关键的技术为LST降尺度技术(Zhan et al,2013;Chen et al,2014)。目前LST降尺度方法主要有三大类:时空相邻融合法、机器学习法和统计回归法。其中,时空相邻融合法是对具有不同时间尺度和不同空间尺度的同一遥感参数数据(如LST、辐亮度、反射率等),利用粗、高分辨率影像光谱相似性原理和混合像元分解法,并结合时空相邻差异与地表类型差异构建尺度转换因子从而达到LST降尺度,主要代表性模型有时空自适应反射率融合模型(STARFM)(Gao et al,2006)、自适应时空融合变化检测模型(STAARCH)(Hilker et al,2009)、增强时空自适应反射率融合模型(ESTARFM)(Zhu et al,2010;Long et al,2020)、自适应数据融合模型(FSDAF)(Zhu et al,2016),这些模型主要针对具有相似热红外光谱特征的粗、高分辨率LST融合,而微波与热红外光谱特征存在明显差异,因此这些方法难以应用于微波LST降尺度中。而机器学习法通常采用神经网络(ANN)和随机森林(RF)模型进行降尺度,如Shwetha and Kumar(2016)采用神经网络模型,考虑地形、土地覆盖类型、微波植被指数等对AMSR-E/2 25 km 亮温降尺度到1 km来模拟全天候LST;Yoo et al(2020)针对韩国地区采用RF模型进行AMSR-2 LST降尺度,除了考虑地形因子和不透水盖度等外,还加入了该地区与LST有关的3个年尺度参数(年均LST、LST振幅和相对于春分的LST时相差),而这些变量需要利用长时间序列LST资料估算获取;Zhong et al(2021)针对中国青藏高原地区利用AMSR-2卫星数据LST降尺度中,在RF模型中考虑了地形因子、归一化植被指数(NDVI)和3个微波通道垂直极化亮温等。由于机器学习模型需要构建大量的代表性训练样本,且输入的变量较多不宜获取,建模过程较为复杂,建立的模型在其他地区并不一定适用。

基于统计回归的LST降尺度方法假定在低空间分辨率像元尺度上建立的LST与其他相关地表参数(或回归因子)之间的统计关系具有空间尺度不变性,可将其应用到高空间分辨率像元尺度上,因此,该方法不受光谱特征的限制。最初广为应用的LST统计降尺度方法是DisTrad(disaggregation procedure for radiometric surface temperature)模型(Kustas et al,2003),该方法将LST与NDVI的负相关关系应用于LST的降尺度中;考虑到NDVI在高密度植被区的饱和性,Agam et al(2007)利用植被覆盖度替代NDVI发展了TsHARP(thermal data sharpening)模型进行LST的降尺度。进一步,考虑到城市地表的特性,Dominguez et al (2011)在NDVI的基础上加入地表反照率,可以有效提高城市地区LST降尺度精度;Wang et al (2020)研究显示,在城市地区采用归一化建筑指数(NDBI)较NDVI具有更好的LST降尺度效果。以上研究主要利用单变量或者多变量与LST之间回归关系来预测LST,这些回归模型均假定LST和回归变量之间的关系具有空间不变性。事实上,LST与这些回归变量(例如NDVI、地表高程DEM)之间的关系是随地理位置变化的,例如,Jeganathan et al (2011)基于TsHARP模型对比了全局与局部并结合土地利用的分层LST降尺度模型,研究发现,局部的LST模型最为可靠。因此,由于地形地理因素,各回归变量如LST、NDVI、NDBI存在空间异质性,随着样本的地理空间位置改变,变量之间的关系结构也发生相应变化,即LST与回归变量之间的关系具有空间局地性特征。由此,本文引入考虑局地空间异质性的地理加权回归(GWR)法(Duan and Li,2016)来开展FY-3D/MWRI LST从25 km 分辨率降尺度到1 km 分辨率研究,并与过境时间相同的FY-3D/MERSI LST进行融合,从而开展基于FY-3D的全天候1 km LST融合研究,这对于发展基于国产气象卫星的长时间序列卫星气候数据集具有积极意义。

1 试验数据

1.1 研究数据

选取中国区域一年代表月份(1、4、7、10月)典型日(2019年7月14—16日、2019年10月14—16日、2020年1月12—14日、2020年4月16—18日)白天FY-3D/MERSI LST和25 km FY-3D/MWRI LST白天(升轨)产品以及所在旬FY-3D/MERSI NDVI产品(王圆圆和李贵才,2022),这些产品均来源于中国气象局风云卫星产品官方网站“风云卫星遥感数据服务网”(http:∥satellite.nsmc.org.cn/portalsite/default.aspx)。其中FY-3D/MERSI LST产品空间分辨率为1 km,采用Hammer投影,LST主要采用Becker局地分裂窗改进算法(董立新等,2012;杨军和董超华,2011)反演得到;FY-3D/MWRI LST产品空间分辨率为25 km,采用全球圆柱等积投影(EASE-GRID),LST反演算法采用基于土地覆盖分类的多通道回归模型(杨军和董超华,2011),并假设每种类型地表在各个被动微波通道具有一致的比辐射率;引入土地覆盖分类保证了每种类型的发射率的相对稳定,可提高LST的反演精度(武胜利和杨虎,2007)。

文中所涉及的中国地图基于国家测绘地理信息局标准地图服务网站下载的审图号GS(2019)1822号的标准地图制作,底图无修改。

1.2 产品验证数据

由于没有足够的均一性站点LST观测数据进行1 km尺度的LST验证,这里选取由国家青藏高原数据中心(TPDC)网站(https:∥data.tpdc.ac.cn/zh-hans/)公开发布的“中国陆域及周边逐日1 km 全天候地表温度数据集”(简称TPDC LST)(周纪等,2021)对FY-3D 1 km LST融合结果进行评估。TPDC LST基于1 km MODIS/Aqua LST产品和0.25°空间分辨率GLDAS(Global Land Data Assimilation System)以及0.0625°空间分辨率CLDAS(China Land Data Assimilation System)等再分析数据生成(Zhang et al,2021),其中再分析数据主要用于云下LST的融合,且CLDAS主要针对中国区域,并融合了地面气象站点LST观测数据(孙帅等,2017;2022;师春香等,2018;王莉莉和龚建东,2018);利用分布于黑河流域、东北、华北和华南地区的15个站点实测数据对TPDC LST产品评估表明,其平均偏差(MBE)为-1.17～-0.06 K,均方根误差(RMSE)为1.52～3.71 K,且在晴空与非晴空条件下无显著区别。

此外,为了评估FY-3D/MERSI LST质量,这里还选取了与FY-3D/MERSI LST日期相同的MODIS Aqua LST产品V6版本(MYD11A1)进行分析,空间分辨率为1 km,采用正弦曲线投影,数据来源于美国航天局网站(https:∥earthdata.nasa.gov/)。

2 研究方法

2.1 地理加权回归模型

地理加权回归(GWR)方法是传统标准回归方法(如普通最小二乘方法)的拓展,该方法是进行局部而不是全局参数估算(Fotheringham et al,2002)。通过利用地理空间变化的回归系数,来研究自变量与因变量之间的动态回归关系。GWR模型可表示为:

(1)

式中:μi和υi是第i个位置的地理坐标,yi和χik分别是第i个位置的因变量和第k个自变量,β0和βk分别为第i个位置的回归模型的截距和系数(斜率),εi为第i个位置的回归残差。

β(μi,υi)=[XTW(μi,υi)X]-1XTW(μi,υi)Y

(2)

式中:β(μi,υi)是各回归系数β的无偏估计,W(μi,υi)是权重矩阵,其确保离目标点更近的相邻观测点有更大权重,X和Y分别是自变量和因变量矩阵。

空间权重W(μi,υi)是GWR模型的核心,常用的有距离阈值函数法、距离反比法、指数函数法、高斯函数法和双平方函数法,本研究采用自适应双平方函数(bi-square)法:

(3)

式中:Wi,j是当前回归点位置i与邻近观测点位置j之间的权重,dij是两点之间的欧式距离,hi是自适应核的波宽(或带宽)。在本研究中利用改进的AIC(Akaike information criterion)准则来确定宽带:

(4)

式中:n是观测样本数,S是帽子矩阵,tr(S)为矩阵的秩,RSS是剩余平方和。

2.2 LST降尺度变量选择

在LST降尺度中,选择合适的辅助变量进行LST降尺度是非常关键的。许多研究表明,NDVI和DEM与LST关系密切,这是由于作为与地表覆盖相关的植被活动和生物量的指示器,NDVI可用来考虑不同地表覆盖类型对地表热过程的影响,而DEM被认为是表征LST变化的另一个重要因素(吴芳营等,2022)。此外,地理经度(Lon)反映了从海岸到陆地区域土壤湿度对LST的影响,地理纬度(Lat)反映了不同纬度带太阳辐射对LST的影响(Ke et al,2013)。另外,一些研究还表明在LST降尺度过程中增强型植被指数(EVI)较NDVI具有更好的表现(Qiu et al,2018),归一化沙尘指数(NDSI)在荒漠地区有较好表现(Pan et al,2018),在半干旱地区及城市地区归一化建筑指数NDBI较NDVI具有更好表现Wang et al(2020)。

本研究针对FY-3D/MWRI LST建模,选择变量的一个重要原则是考虑数据业务生产的便利性,尽量避免选择难以获取的变量,而是从FY-3D产品中直接获取相关变量。由于受云雨影响,1 km分辨率的 FY-3D MERSI日NDVI产品存在大量缺值,而旬NDVI产品则基本上克服了这种缺值问题。假定旬内NDVI变化很小,由此可选用FY-3D旬NDVI合成产品作为辅助变量;此外旬NDVI合成产品中包含了短波红外通道(中心波长为1.380 μm)和近红外通道(中心波长为0.865 μm)反射率值,由此,可以基于短波红外通道反射率RSWIR和近红外通道反射率RNIR,估算得到归一化建筑指数(NDBI):

(5)

由此,本研究选择FY-3D旬归一化植被指数NDVI、NDBI产品和DEM作为LST降尺度变量;由于地理经度Lon和纬度Lat在GWR模型中己经是输入参数,因此不再于模型中显示。

2.3 FY-3D/MWRI LST与MERSI LST融合

FY-3D/MWRI 25 km LST与FY-3D/MERSI 1 km LST融合技术流程如图1所示,主要包括FY-3D/MWRI LST订正、基于GWR模型的FY-3D/MWRI LST降尺度、轨道间隙(Gap)补值等步骤。

图1 逐日FY-3D 25 km MWRI LST与MERSI 1 km LST融合技术流程图

2.3.1 FY-3D/MWRI LST订正

对2019年7月14—15日、2019年10月15—16日和2020年4月17—18日FY-3D/MWRI LST分析显示(图2),晴空天气条件下白天FY-3D/MWRI 25 km LST较FY-3D/MERSI 1 km LST明显偏低,而且是系统性的偏低,平均偏差MBE(MWRI LST与MERSI LST之差平均值)小于-5 K,部分在-10 K以下,这与高浩等(2018)对FY-3C/MWRI LST评估显示其LST明显偏低结果相似,表明FY-3/MWRI LST存在明显的低估。由于MWRI LST与MERSI LST存在明显空间相关,决定系数R2一般在0.75以上,因此可以利用线性回归模型基于FY-3D/MERSI LST对FY-3D/MWRI LST进行偏差订正,在此基础上开展两者融合,主要步骤为:

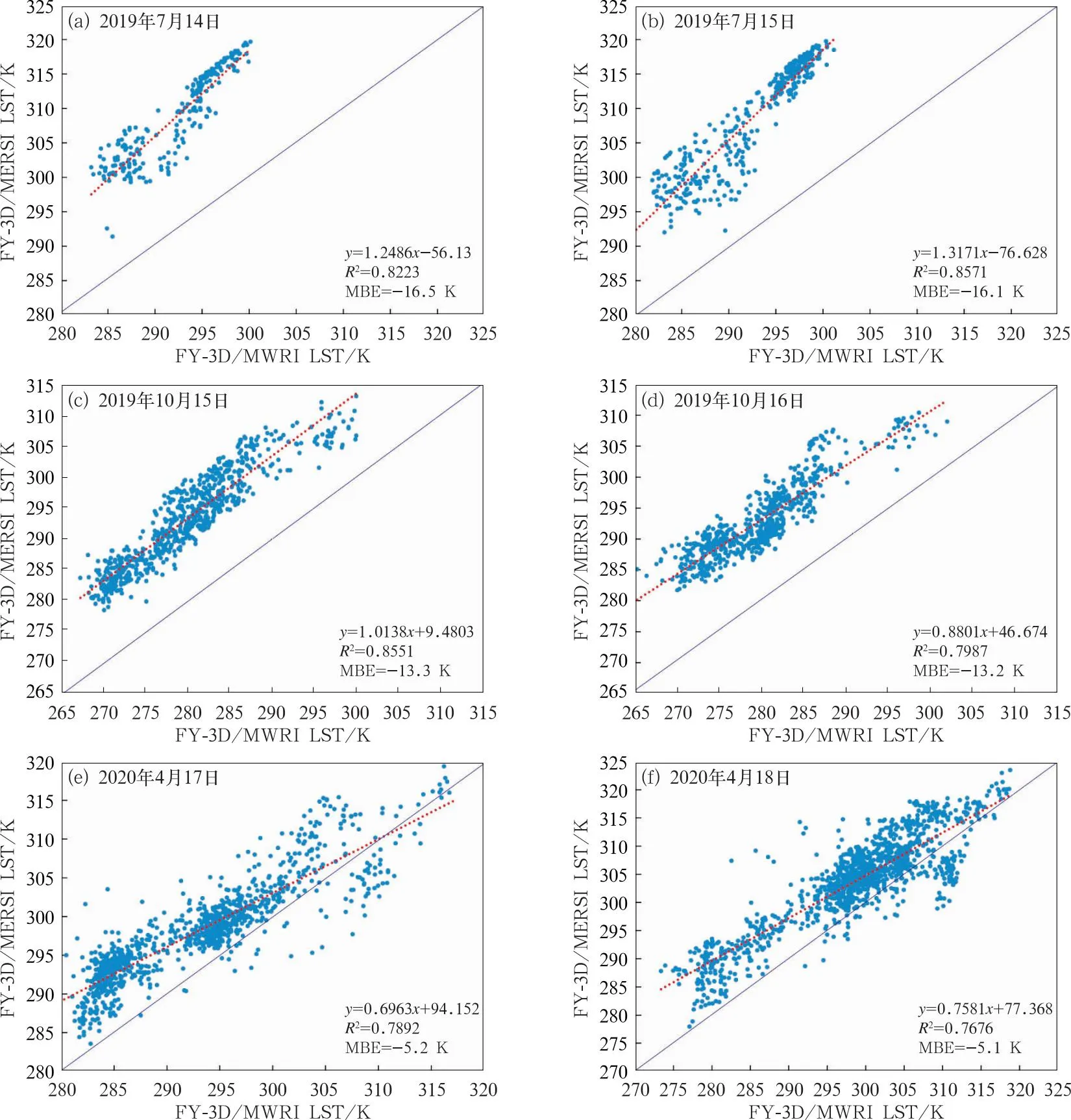
注:深蓝色线为LST 1∶1线,红色线为线性回归方程线。

(1)25 km分辨率晴空率判别:根据1 km分辨率MERSI LST文件中的有效值,估算25 km分辨率的晴空像元百分比;同时对MERSI 1 km分辨率LST文件,利用均值法重采样生成MERSI 25 km分辨率LST。

(2)MWRI LST偏差订正:根据25 km分辨率的晴空像元百分比,取值为1.0时(完全晴空),获取相应位置的FY-3D/MWRI 25 km分辨率LST值和重采样后的25 km分辨率的MERSI LST值,对这二者LST进行最小二乘法线性拟合,生成自变量为MWRI LST、因变量为MERSI LST的关系式,依据该关系式对原始FY-3D/MWRI 25 km分辨率LST进行偏差订正。

经过上述步骤后,MWRI 25 km LST偏低问题可得到明显改善所示,如图3所示,2019年7月15日、2019年10月15日和2020年4月17日MWRI LST值得到明显提升,与FY-3D LST的平均绝对偏差分别降至2.2、2.3和2.7 K。

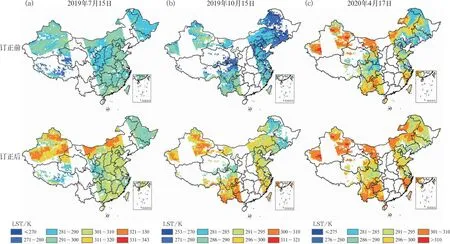
图3 典型日期下的FY-3D/MWRI 25 km LST订正前后对比

2.3.2 基于GWR模型的FY-3D/MWRI LST降尺度

对经过系统偏差订正后的FY-3D/MWRI 25 km LST,利用GWR模型降尺度到1 km LST,主要步骤包括:

(1) 空间聚合:根据有效像元平均法将当日所在旬合成1 km NDVI、NDBI影像以及DEM进行空间聚合,生成25 km分辨率的NDVI、NDBI及DEM影像。

(2) GWR建模:利用GWR法建立订正后25 km 分辨率MWRI LST与25 km分辨率NDVI、NDBI和DEM之间的动态回归关系,其可表示为:

LSTi=β0(μi,υi)+β1(μi,υi)NDVIi+

β2(μi,υi)NDBIi+β3(μi,υi)DEMi+εi

(6)

各参数含义见式(1)。由于覆盖中国区域的FY-3D/MWRI LST产品需要3条轨道,而不同轨道相隔较远,中间存在大量无值区域,如图4所示,为避免样本在空间不均一带来的误差,在建立该景LST地理加权回归模型时,需对每条轨道覆盖中国区域LST样本单独进行建模,即每景中国区域MWRI 25 km LST影像需要建立3个GWR回归模型。

图4 典型日期下的FY-3D/MWRI 25 km LST有效覆盖范围

(4)1 km LST模拟:利用前面得到的1 km回归系数和1 km 分辨率NDVI、NDBI和DEM等变量,进行1 km LST模拟预测:

(7)

2.3.3 当日1 km LST融合

基于当日FY-3D/MERSI 1 km LST与降尺度后的MWRI 1 km LST进行融合,即:MERSI LST有值部分仍保留,缺值部分用降尺度后的1 km LST模拟值代替。

2.3.4 Gap补值

由于MWRI全球各扫描轨道之间尤其是中低纬度存在明显空隙(Gap),且每天均不固定,如图4所示,因此MWRI和 MERSI融合后的LST产品仍在Gap区域存在大量缺值,在这里采用Duan et al(2017)的补值法进行Gap处理,即假设当天云区下的LST值与前1天和后1天云区下的LST值相当,因此根据1 km云区Gap位置,需读取前后各1天融合后的1 km LST值进行补值。如果前后2天均无LST值,仍作为缺值处理。

2.4 Duan et al(2017)LST降尺度法

为了对比本文25 km FY-3D/MWRI LST降尺度效果,这里引入Duan et al(2017)基于MODIS/Aqua 1 km LST对AMSR-E 25 km LST进行LST降尺度的方法(以下简称Duan法),其核心思想是把AMSR-E LST 25 km 分辨率的像元分为三类:完全晴空、完全云覆盖、部分云覆盖进行融合,针对每类像元分别进行处理:

(1)完全晴空像元,融合后的该像元在1 km分辨率的LST仍为原始MODIS LST值。

(2)完全云覆盖像元:利用该25 km像元内1 km 分辨率的DEM值进行海拔高度差订正(海拔每下降1 km,LST降低6.5 K)。

(3)部分云覆盖混合像元:基于混合像元分解法原理,把25 km混合像元LST近似看成晴空子像元LST及面积比例和云覆盖子像元LST及面积比例的线性加权和,根据该混合像元LST、晴空子像元平均LST及面积比例、云覆盖子像元面积比例,即可求取所有云覆盖子像元平均LST,然后根据子像元的海拔高度进行海拔订正,即可得到每个云覆盖子像元LST。

3 结果分析

3.1 GWR模型效果分析

对MWRI 25 km LST 模拟分别选用NDVI、NDBI、DEM和NDVI、DEM的GWR回归模型分析结果如图5所示:针对中国区域,在NDVI和DEM基础上,加入NDBI后,25 km LST模拟效果总体决定系数R2得到提高;而所有局地回归模型平均决定系数R2增加。

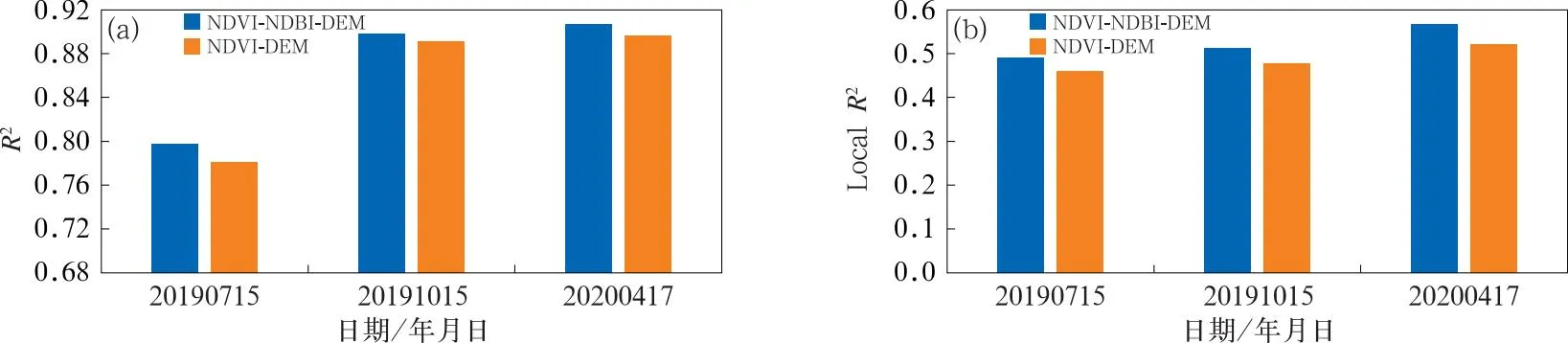
图5 基于FY-3D/MWRI LST的不同回归变量建立的GWR模型LST模拟结果比较

对2019年7月14—16日、2019年10月14—16日、2020年4月16—18日FY-3D/MWRI LST建立的GWR模型拟合效果(图6)可以看出,GWR模型对MWRI LST模拟的R2为0.77～0.93,均方根误差(RMSE)为1.2～3.2 K;与传统的TsHARP模型(Agam et al,2007)相比较,GWR模型的决定系数R2显著提高(平均值从0.36提高到0.85),而RMSE明显降低(平均值从4.3 K降低到2.2 K)。该结果表明GWR模型比TsHARP模型可更好地预测大范围区域LST。

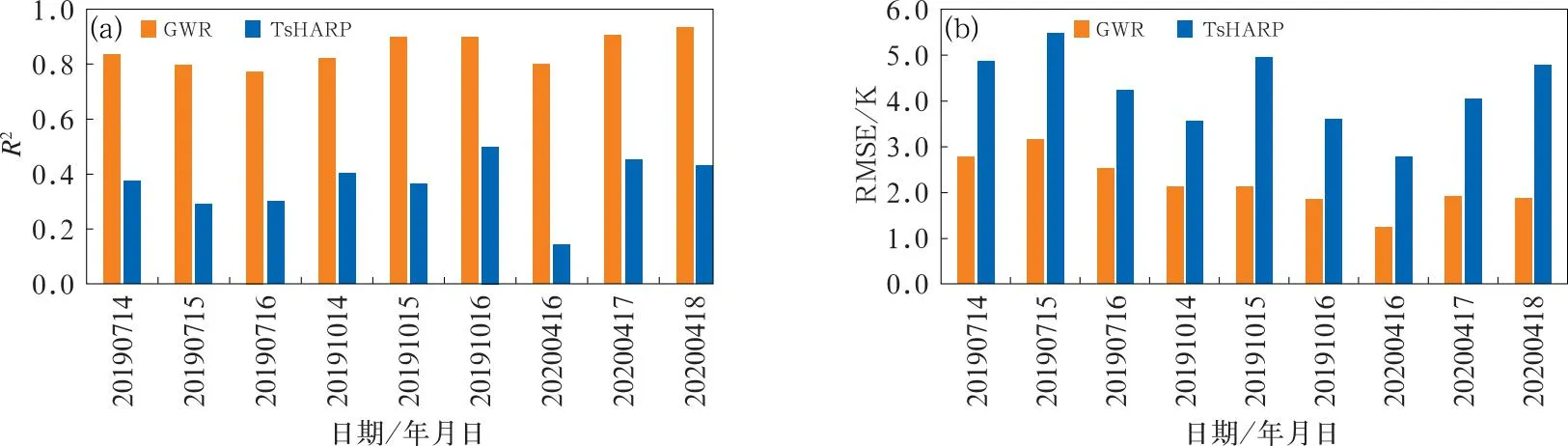
图6 GWR模型与TsHARP模型对FY-3D/MWRI LST模拟结果的比较

如图7所示为2020年4月17日FY-3D 25 km MWRI LST GWR模型回归系数1 km分辨率空间插值结果,各回归系数存在明显空间差异,而局地回归模型模拟效果也存在较大空间差异,但局地决定系数R2一般在0.40以上,平均为0.568。

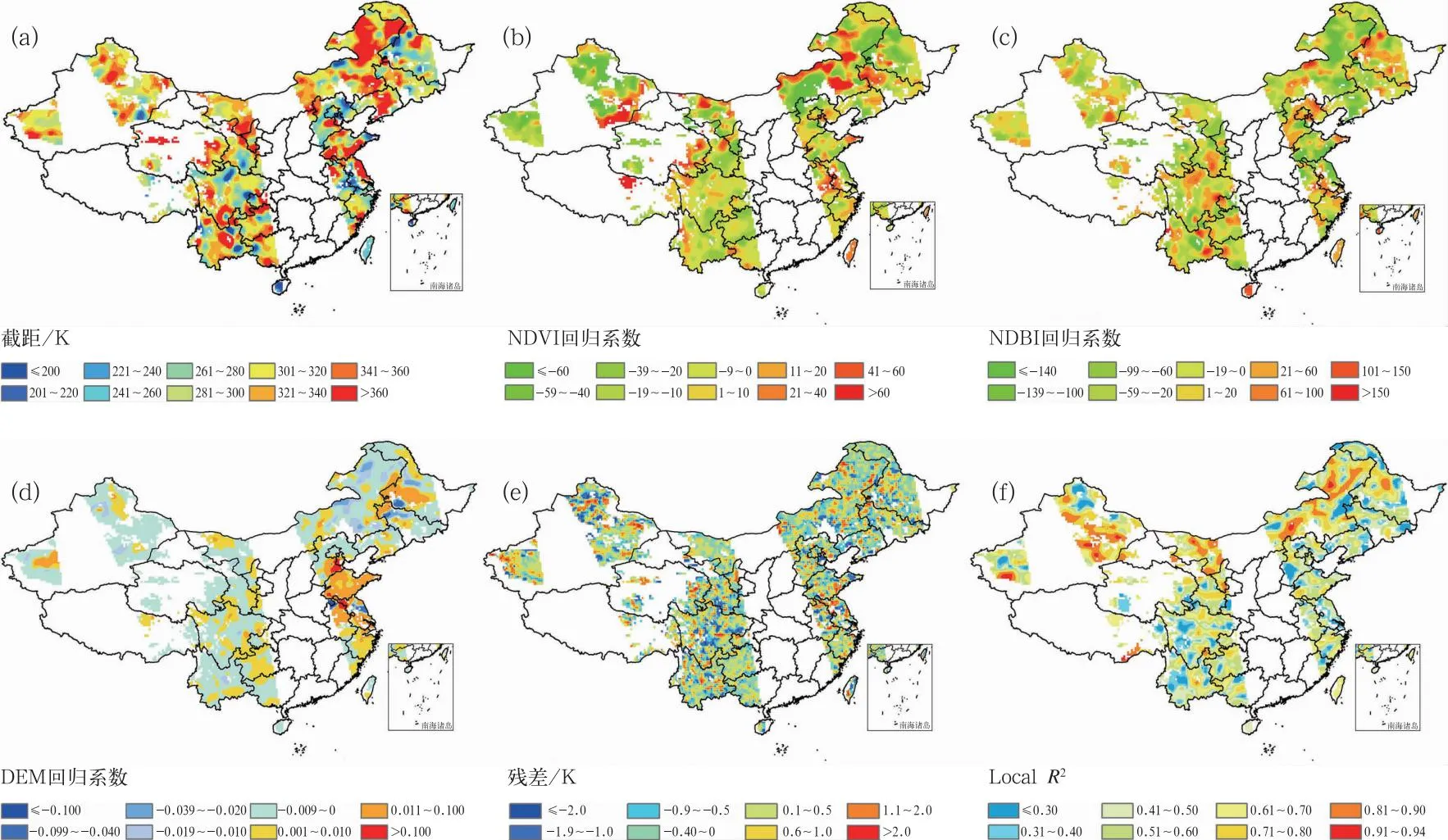
图7 2020年4月17日FY-3D/MWRI 25 km LST GWR模型回归系数空间插值1 km结果

3.2 GWR模型降尺度效果

如图8所示为2019年10月15日FY-3D/MWRI 25 km LST降尺度到1 km前后LST对比,可以看出,基于GWR模型,25 km LST降尺度到1 km后,1 km LST空间分布与原始25 km LST具有良好一致性,空间细节增加明显,还能凸显出北京中心城市地区的高温现象,而在原始25 km LST影像中这种高温现象不明显。

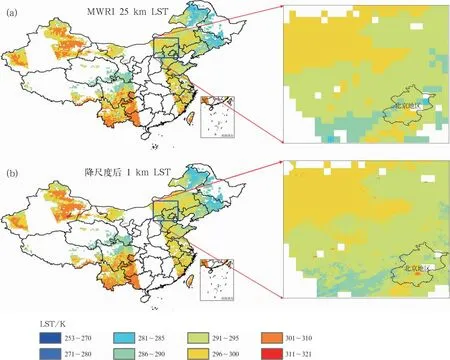
图8 2019年10月15日FY-3D/MWRI 25 km LST降尺度到1 km前后LST对比

3.3 当日LST融合效果

如图9所示为2019年7月15日FY-3D/MWRI 25 km LST降尺度到1 km前后LST对比,可以看出,与原始MWRI LST相比,采用Duan法融合后的LST与本算法融合的LST空间分辨率明显增加,且均具有较好的空间分布一致性,但Duan法出现明显“斑块”效应,且易出现局部低值现象(图中蓝色圆圈所示)。斑块化的原因是由于采用海拔差进行25 km LST降尺度订正时,由于不同尺度海拔存在明显差异造成降尺度后的相邻像元LST不连续;局部低值则是采用的混合像元(包括晴空和云覆盖区)法所导致,例如25 km分辨率像元LST为295 K,晴空覆盖率为0.90,如果晴空子像元LST为300 K,则云覆盖区域LST仅为250 K,明显偏低;而本文算法(GWR)则有效消除了“斑块”效应和局部低值问题。

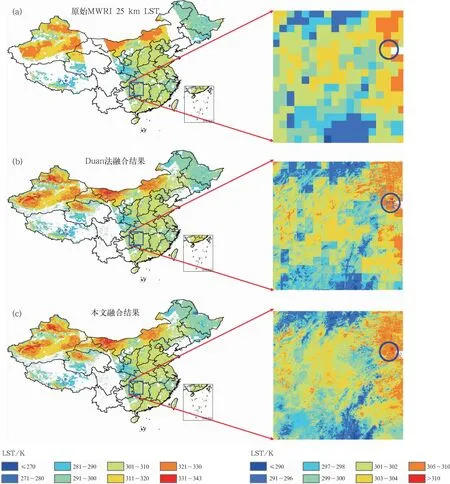
注:圆圈为降尺度中出现的局部低值现象。

3.4 最终LST融合结果

在当日FY-3D 1 km MERSI LST与25 km MWRI LST融合基础上,进行前后1天融合LST轨道间隙(Gap)区域补值,生成最终当日LST融合结果,如图10所示为2019年7月15日、2019年10月15日、2020年4月17日生成的当日FY-3D/MERSI 1 km LST(图10a)、与FY-3D/MWRI 25 km LST融合后生成的当日1 km LST(图10b)以及前后1天Gap LST补值结果(图10c),可见当日FY-3D 1 km MERSI LST有值率(有效值面积百分比)仅为22.4%～36.9%,与25 km MWRI LST融合后,LST有值率增加到59.3%～65.3%,经过前后1天LST补值后,LST有值率增加到69.3%～80.7%,但仍远未达到全天候LST的融合比例(100%)。

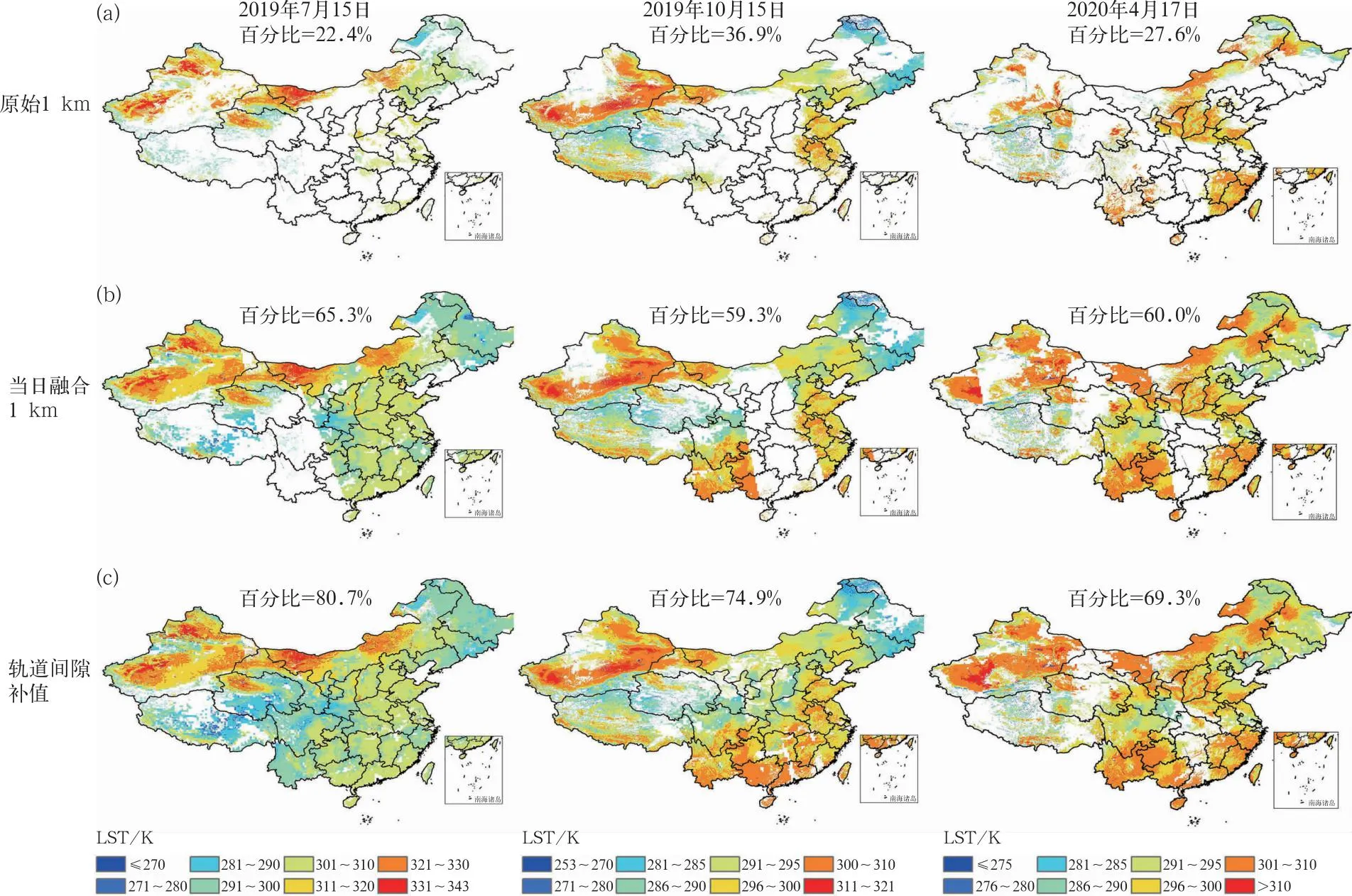
图10 典型日期下(a)FY-3D/MERSI 1 km LST,(b)当日1 km融合结果,(c)轨道间隙前后1天补值结果及LST有效值占中国区域面积百分比

3.5 融合LST质量分析

3.5.1 LST融合产品缺值分析

为了分析LST融合产品有值率明显小于全天候比例(100%)原因,这里统计了FY-3D/MWRI卫星轨道(FY-3D/MWRI Orbit)覆盖中国区域百分比与25 km 分辨率MWRI LST有值率,以及1 km FY-3D/MERSI LST和时间相近的MODIS/Aqua LST有值率,如图11所示。可以看出,FY-3D/MWRI卫星轨道一般覆盖中国区域64.0%～73.5%,而MWRI LST有值率则明显偏低,尤其是冬季如2020年1月12—14日MWRI LST有值率仅为7.0%～11.1%,这也是本文未对冬季FY-3D/MWRI LST与MERSI LST进行融合的主要原因;而其他季节MWRI LST有值率为38.2%～56.9%,较相应MWRI轨道覆盖率降低15.0%～27.6%;结合图4、图8和图9 MWRI过境轨道LST有效值分析,缺值主要出现在青藏高原地区与部分低温地区,这与FY-3D/MWRI LST反演之前需要做冰雪和降雨等像元剔除原因密切相关(杨军和董超华,2011),而且MWRI LST反演算法在冬天容易把大量低温像元识别为冰雪,因此造成冬季MWRI LST大量缺值,而在其他季节也容易把青藏高原低温地区识别为冰雪,从而造成青藏高原地区与低温地区MWRI LST缺值明显。

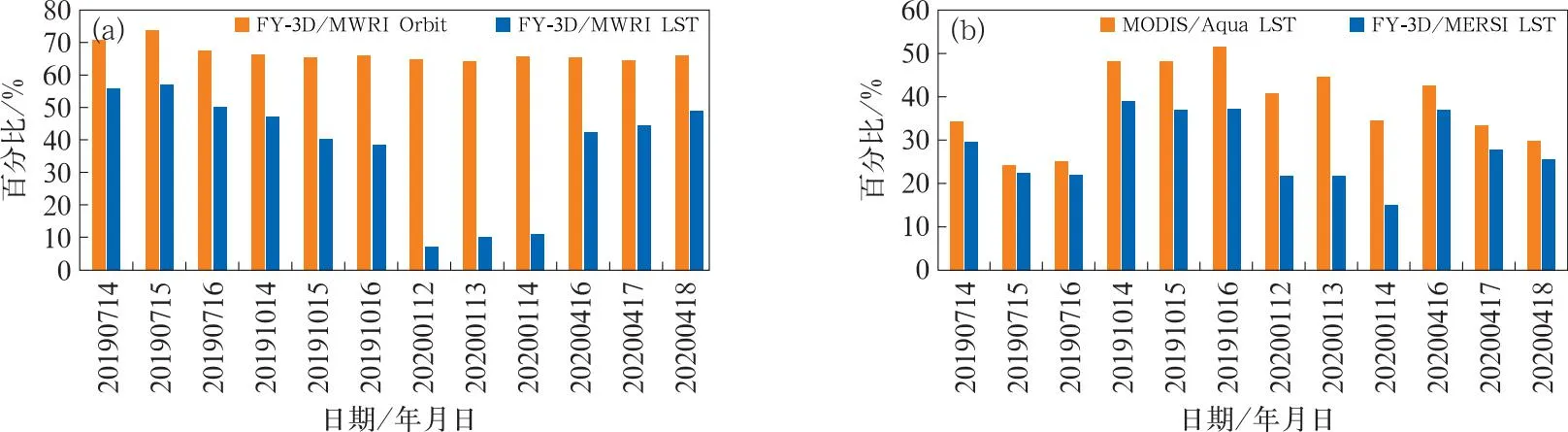
图11 (a)FY-3D/MWRI卫星轨道覆盖面积百分比与25 km 分辨率MWRI LST有值率,(b)1 km FY-3D/MERSI LST和同时间MODIS/Aqua LST有值率对比

另外,FY-3D/MERSI LST的有值率仅为15.1%～38.9%,较相应MODSI/Aqua LST有值率偏低1.8%～22.8%,其中冬季2020年1月12—14日偏低均在19%以上,而其他季节也明显偏低,表明FY-3D/MERSI LST很可能过高地估计了云覆盖率或冰雪覆盖率(目前FY-3对冰雪地区未做LST反演),而在冬季尤为明显。

综上所述,FY-3D/MWRI 和FY-3D/MERSI LST均存在缺值率较为明显问题,这是两者LST融合产品有值率未能达到全天候比例(100%)的一个重要原因。

3.5.2 LST融合产品精度分析

在这里利用全天候1 km TPDC LST产品对1 km FY-3D Fusion LST(融合产品)分为晴空、云天和全天候条件下进行产品交叉验证评估。为了减少产品之间的配准误差以及不同点扩散函数导致的地理定位的不确定性,产品间交叉验证时使用最小一致空间支持法(MCSS)(Baret et al,2013),即像元值采用3×3像元中有效像元比例不低于5/9的情况下有效像元平均值。基于MCSS法,对2019年7月15日、2019年10月15日、2020年4月17日1 km LST融合产品评估结果如图12所示,无论是晴空、云天还是全天候下白天1 km FY-3D/MERSI LST与MODIS/Aqua LST存在明显空间相关性,其中晴空天气下R2为0.718～0.914(平均为0.813),平均偏差(MBE)为-0.9～0.5 K,RMSE为2.6～4.9 K(平均为3.5 K);云天下R2较晴空有明显下降,为0.457～0.628(平均为0.530),MBE为-1.6～0.9 K,RMSE为4.1～6.1 K(平均为5.1 K);而全天候则是晴天和云天综合的结果,R2为0.503～0.787(平均为0.660),MBE为-1.5～0.8 K,RMSE为3.6～5.8 K(平均为4.8 K)。

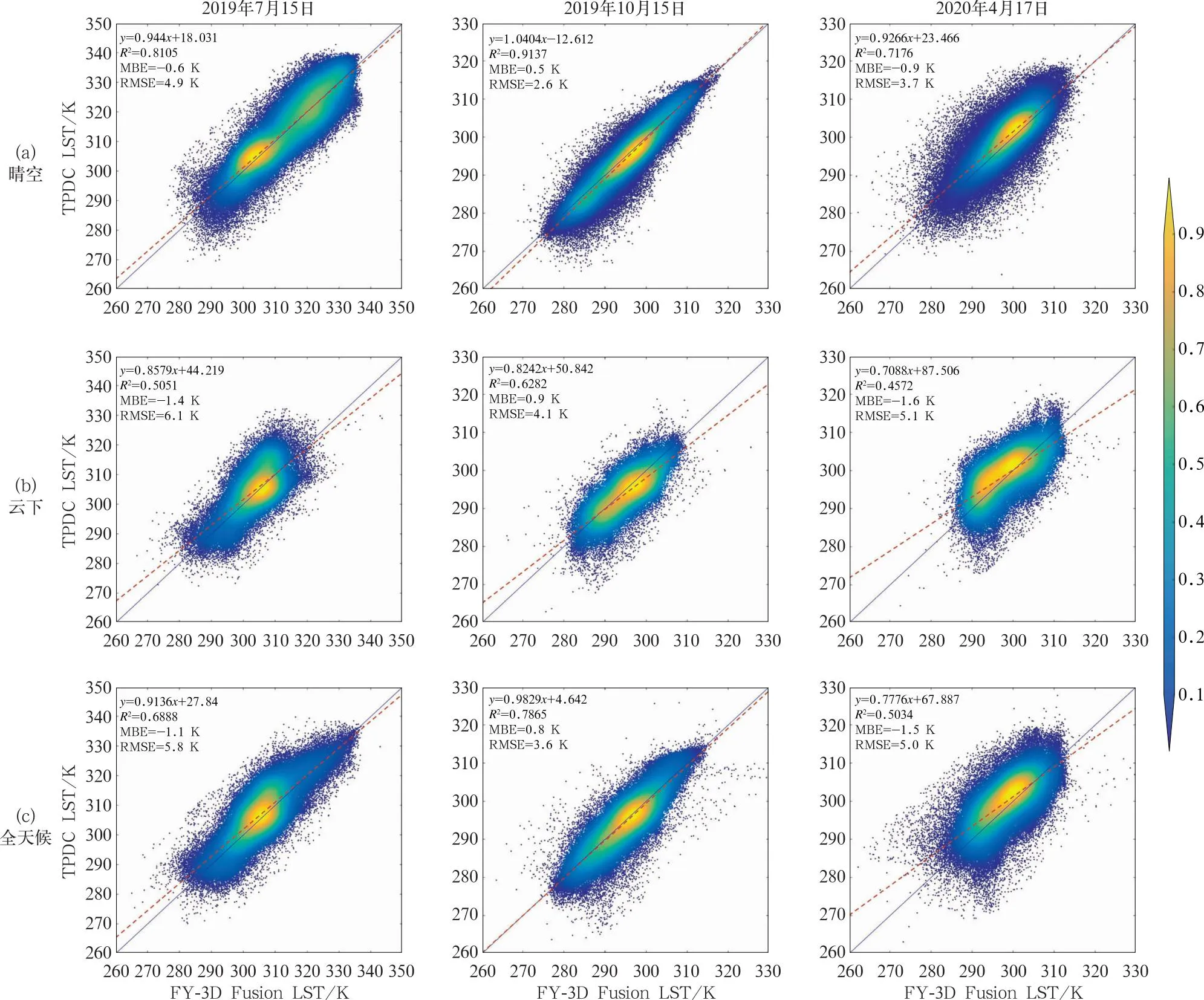
注:深蓝色线为LST 1∶1线,红色线为线性回归方程线。

除了利用站点和已有LST产品进行评估外,与其他类似相关LST融合产品的精度相互比较也能一定程度看出该产品的质量总体状况(Duan et al,2017;Yoo et al,2020;Zhong et al,2021)。表1列出了近些年已有研究对基于微波传感器(主要为AMSR-E/2)与光学传感器(主要为MODIS Aqua)1 km LST白天融合产品精度评估结果。由于采用的不同的融合算法和评估方法,各融合LST产品精度变化较大,如决定系数R2变动较大(0.51～0.98),全天候条件下Yoo et al(2020)的RMSE最小(1.9～3.3 K),而Xu et al(2019)的RMSE可达4.27～8.29 K;此外,晴空天气下的LST精度一般好于云下,如Duan et al(2017)、Zhang et al (2020)和Zhong et al(2021),但晴空LST的RMSE一般小于4.2 K,云下的RMSE可达6 K以上。与这些已有研究结果相比,本文基于FY-3D的LST融合产品精度虽稍差于基于AMSR-E/2和MODIS/Aqua LST的融合产品,但无论是平均R2,还是平均RMSE,均在上述研究结果最大最小精度范围之内,表明基于本文的融合方法,仍可以实现FY-3D MWRI与MERSI LST的有效融合。

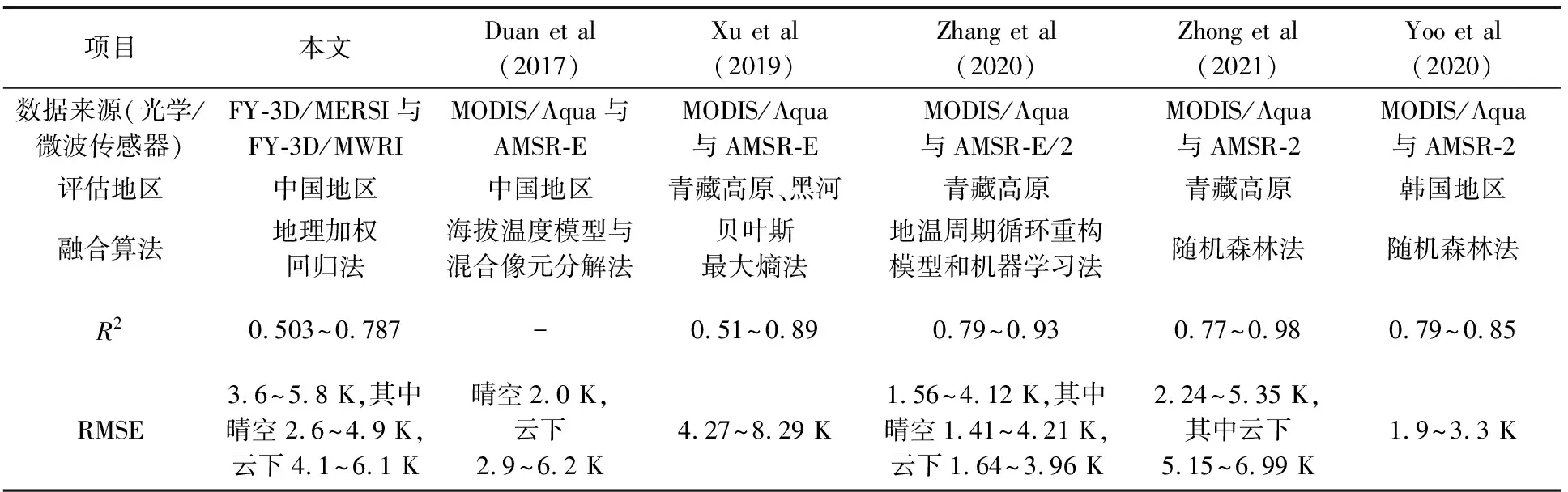
表1 本文1 km LST 融合产品精度与近些年已有研究结果(白天)比较

4 结论与讨论

4.1 结 论

1 km分辨率的全天候陆表温度(LST)已经成为全球与区域气候变化领域研究的迫切需求,目前还没有基于国产卫星的1 km分辨率的全天候LST产品。FY-3D 中分辨率成像仪Ⅱ型(MERSI-Ⅱ)提供了1 km分辨率的晴空LST产品,而FY-3D微波成像仪(MWRI)能获取不受云影响的LST产品,但空间分辨率较粗(25 km),因此可结合两者优势开展全天候1 km分辨率LST的融合研究。本文基于局部参数估计的地理加权回归(GWR)方法,选择海拔、FY-3D 归一化植被指数(NDVI)和归一化建筑指数(NDBI)等变量开展25 km MWRI LST降尺度到1 km,并针对MWRI过境轨道之间间隙(Gap)无LST情况,利用前后1天融合后的1 km LST云覆盖像元LST进行补值,从而开展了基于FY-3D的全天候LST融合产品研究。研究结果表明:

与传统的全局参数回归方法TsHARP相比,基于GWR建立的回归模型预测的MWRI LST的R2从0.363增加到0.85,均方根误差从4.26 K降至2.17 K。基于该回归模型对FY-3D/MWRI 25 km LST降尺度到1 km LST,可以有效解决传统的基于海拔与混合像元分解的LST降尺度方法存在明显“斑块”效应和局地温度偏低等问题。对多个典型日期中国FY-3D MERSI和MWRI 1 km LST融合效果表明,原始1 km晴空的LST有值率为22.4%～36.9%,融合后的1 km LST有值率可达69.3%～80.7%;利用基于MODIS LST和GLDAS/CLDAS的全天候1 km LST产品对本文1 km 融合LST评估表明,基于FY-3D的融合LST的空间决定系数R2为0.457～0.914,RMSE为3.6～5.8 K,其中晴空2.6～4.9 K,云下4.1～6.1 K,接近或稍差于AMSR-E/2和MODIS/Aqua LST的融合产品精度,表明基于GWR法,可以实现FY-3D/MWRI与MERSI LST的有效融合。

4.2 讨 论

本文基于GWR所获得的融合LST产品最高有值率仅为80%左右,这远未达到100%的全天候LST要求。从前面分析可知,FY-3D 25 km MWRI LST在青藏高原地区和低温地区缺值率较高,而FY-3D/MERSI LST在四季均存在缺值偏高情况,尤其是在冬季。因此,需要一方面改进官网产品FY-3D 1 km MERSI LST的云检测算法;另一方面还需大力改进官网产品FY-3 LST在青藏高原地区和低温地区缺值问题,这是由于这些地区可能判识为冰雪,而FY-3 MWRI LST和MERSI LST目前的算法均不支持对冰雪地区的LST反演,因此开展冰雪地区LST反演是未来提高FY-3 LST有值率的重要发展方向。

另外,基于FY-3D 的LST融合产品误差较大的原因,主要有:

(1)FY-3D/MWRI LST误差:从FY-3气象卫星数据服务官网获取的FY-3D/MWRI LST误差较大。虽然目前基于微波反演得到LST误差较大,一般在3～6 K(Fily et al,2003;Holmes et al,2009;Zhou et al,2015;Shwetha and Kumar,2016),但本文的FY-3D/MWRI LST误差一般在5 K以上,虽然可以利用FY-3D/MERSI LST对其进行偏差订正从而降低误差,但如果MWRI LST与MERSI LST空间相关性并不好时,基于线性回归模型对25 km MWRI LST进行订正仍会造成较大误差,从而造成融合后LST云下误差较大,因此,还需改进FY-3D/MWRI LST反演算法,使其平均误差降至5 K 以下。

(2)FY-3D/MERSI LST误差:从FY-3气象卫星数据服务官网获取的FY-3D/MERSI LST误差较大。从图12晴空天气下的分析可知,FY-3D/MERSI LST与MODIS/Aqua LST(全天候TPDC的晴空像元即为MODIS/Aqua LST)之间的R2为0.717～0.914,RMSE为2.6～4.9 K,这个产品精度均明显低于Du et al(2021)基于改进的分裂窗算法反演的FY-3D/MERSI LST 精度(R2为0.84～0.96,RMSE为1.57～2.52 K)以及Aveni and Blackett(2022)反演的FY-3D/MERSI LST精度(R2为0.92,RMSE为0.75 K)。因此,还需改进FY-3气象卫星数据服务官网的FY-3D/MERSI LST反演算法,使其接近AQUA LST产品精度。

(3)融合算法误差:本文基于GWR建立的局地回归模型一个前提假设是MWRI LST与NDVI、NDBI、DEM、Lat、Lon存在明显线性关系,但受其他因素影响,可能这种关系并不显著,例如图7中建立的局地回归模型平均R2不到0.60,因此势必会存在许多像元LST与回归变量之间的线性相关性比较低,从而会造成LST预测以及降尺度产生明显误差。因此,还需不断改进融合算法来减小LST预测误差。

致谢：感谢国家卫星气象中心董立新正研级高工给予的技术指导。