基于小波降噪的配电网蓄电池系统短路故障检测

徐雄军,路兴帅,夏 翔,吴 优

(国网湖北省电力有限公司孝感供电公司,湖北 孝感 432003)

配电网是整个电力系统中用于实现电能分配的网络系统,随着电能存储技术不断发展,其可为配电网的电能分配提供极大支撑[1]。蓄电池是配电网中一种主要的储能系统,通常情况下蓄电池系统安装在配电网一侧,为配电网的运行提供电能[2]。蓄电池是一种能量转换装置,在充电和放电两种情况下,实现两种能源之间的转换,即化学能和电能的转换。由于蓄电池系统使用寿命较长,对应用环境的要求较低,因此成为配电网运行中的主要储能系统。但蓄电池系统在使用过程中,随着使用时间的增加,电池内部的水分会逐渐流失[3],导致电解液密度上升,蓄电池发生短路故障。蓄电池系统发生短路故障后,会引起开路电压降低,端电压呈线性下降,并在极短时间内降为零,甚至在低温环境中会发生电解液冷凝等一系列现象,影响整个配电网的正常运行。因此,需对配电网中蓄电池系统的短路故障进行检测,对蓄电池出现的故障及时诊断,以便及时维修或者更换蓄电池,保证配电网的运行。小波降噪是一种噪声处理方法,其能够将原始信号与噪声分离,保留原始信号[4]。文献[5]和文献[6]分别研究了基于灰色关联度和基于同步相量的故障定位方法,实现了故障检测。上述方法在检测过程中,会由于噪声的影响而出现误检的问题,并且对于时间序列数据的不平衡处理仍需进一步研究。

本文提出基于小波降噪的配电网蓄电池系统短路故障检测方法,以蓄电池系统电压信号的变化为依据,利用多分辨率小波良好的降噪优势,对蓄电池充电时的电压信号进行降噪。为进一步保证故障检测效果,对电压信号进行降噪处理,为电路故障检测提供可靠的依据。

1 配电网蓄电池系统短路故障检测

1.1 蓄电池系统电压信号降噪

蓄电池系统在充电过程中,其电压信号存在多尺度特征,且存在高、低两种频率的信号[7],因此采用多分辨率小波分析方法对蓄电池电压信号进行降噪。该方法能够完成给定函数的分解,使其形成高、低频率信号,并且该方法具备正交性,能够较好地完成蓄电池系统电压信号的分解和降噪。

设蓄电池系统充电时的电压为Vi(t):

Vi(t)=fi(t)+εi(t)

(1)

式中:fi(t)为没有噪声干扰的电压信号,εi(t)为含噪信号。

(2)

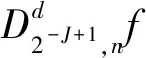
通过上述步骤完成蓄电池系统电压信号降噪后,为避免有效信号的损失,采取消噪方式对其进行处理。消噪的主要目的是降低实际电压信号和降噪后信号之间的误差M(λ)[8]。计算公式为:

(3)

式中:λ为阈值。

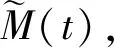
(4)

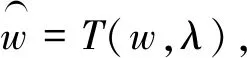
(5)

3)依据n/2个数据获取阈值估计结果,依据该结果可得n个点的阈值估计结果:

(6)

式中:tn/2为估计结果中的n/2个数据。

通过上述步骤即可完成信号的降噪处理,保证了实际电压信号和降噪后信号之间的误差最小。

1.2 基于动态时间规整的短路故障检测

本文采用动态时间规整(dynamic time warping, DTW)方法完成蓄电池系统短路故障检测,该方法能够完成相似度的计算,并且当序列之间的长度存在差异时,依旧具备良好的计算效果。因此,该方法可理解为通过非线性变换对时间序列曲线进行处理,体现样本之间的相似度,且样本位于不同的相位上。

定义Q和C分别表示两个时间序列,前者为待检测序列,由处理后的电压信号组成,后者为参考序列。Q={q(1),q(2),…,q(n)},q(n)为第n个采样点的时间序列;C={c(1),c(2),…,c(m)},c(m)为第m个电压信号。

由于电压信号数据在采集过程中,会存在不平衡数据,导致Q成为不平衡时间序列,为保证短路故障检测结果的精度[9],采用模糊聚类算法对Q中的不平衡数据进行模糊聚类处理。

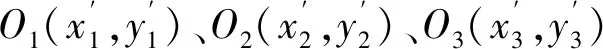
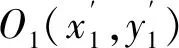
(7)

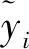
(8)

式中:rand(0,1)表示随机数,取值范围为(0,1)。

(9)

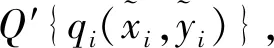
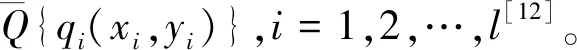
(10)

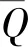
γ(i,j)=D(qi,cj)+min[γ(i,j-1),γ(i-1,j-1)]

(11)

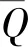
基于动态时间规整的短路故障检测流程如图1所示。

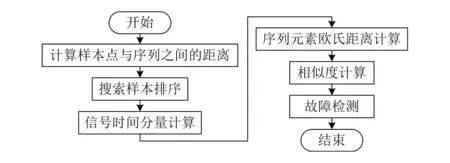
图1 基于动态时间规整的短路故障检测流程

2 验证分析

为验证本文方法在配电网蓄电池系统短路故障方面的应用性能和效果,采用MATLAB软件模拟该短路故障,进行仿真测试。为了模拟蓄电池组不同程度的短路状态,采用6个不同阻值的电阻进行模拟,每一个电阻值均对应一个蓄电池自放电电流,详情见表1。

表1 放电电流详情

模拟配电网的电压为220 V,蓄电池系统由2组108节的蓄电池组成,每节蓄电池的电压为2 V。在模拟过程中,为获取蓄电池的电压信号,反复对配电网蓄电池系统实行充放电,循环次数为30次,充电方式为浮充。在表1中,电阻值越大,表示短路故障程度越小。为了模拟短路故障,在进行充电的前9次循环中不使用并联电阻。而在第12次、18次、21次、27次和30次循环充电时打开开关,这表示信号中存在5次短路故障信号。通过这样的模拟,可以获取充电过程中的电压信号。

采用本文方法进行测试前,需对小波基进行取值,该取值结果与信号的降噪效果直接关联,以信号的均方误差作为参考指标,测试不同小波基取值下的均方误差结果,将最小误差值作为最终小波基。为了更准确地确定小波基的取值范围,随机在获取的电压中抽取两段局部信号进行测试,测试结果如图2所示。

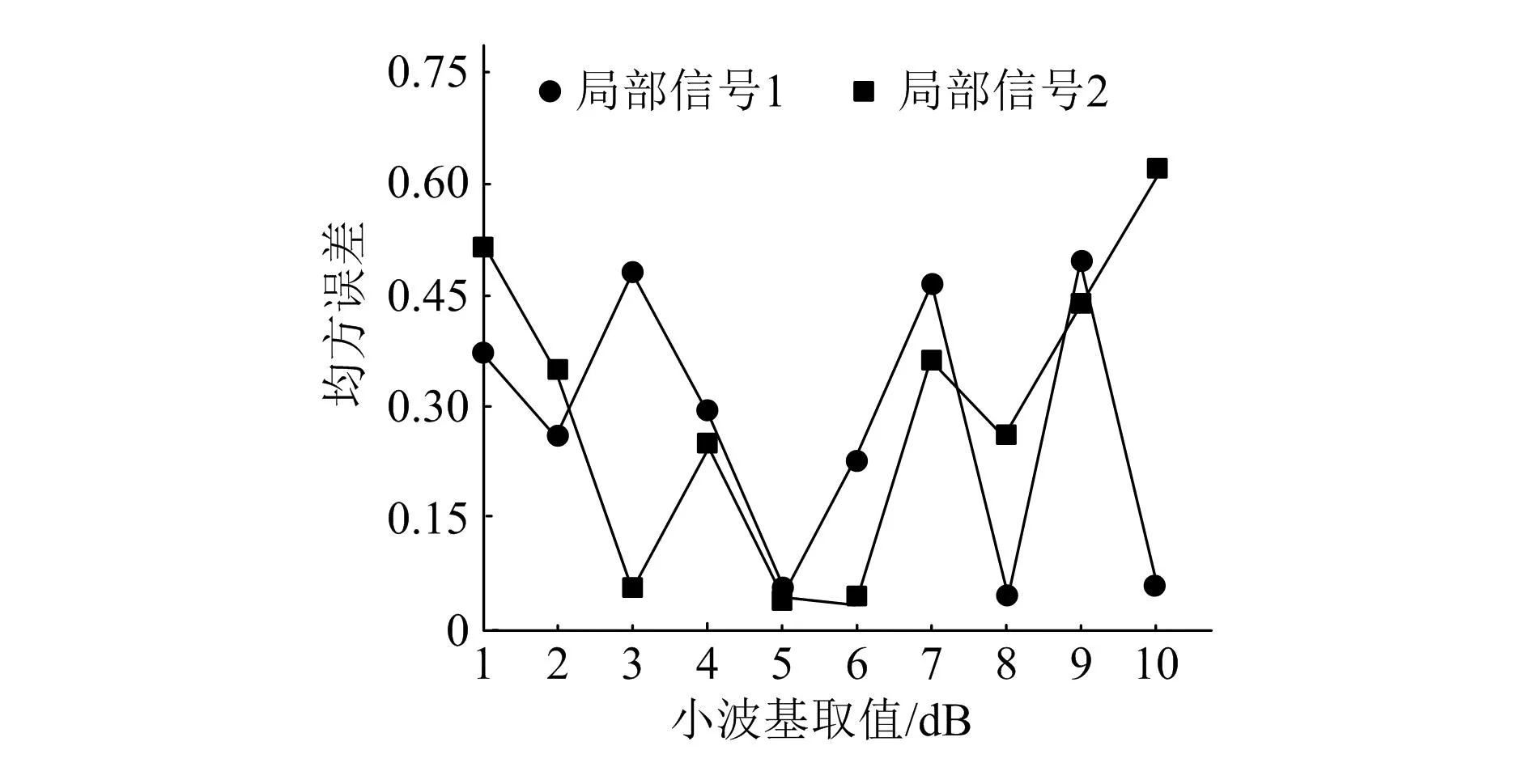
图2 小波基取值测试结果

由图可知,两段局部电压信号的均方误差结果发生不同程度的波动,当小波基取值为3、5、6 dB时,第一段局部信号的均方误差结果较低;当小波基取值为5、8、10 dB时,第二段局部信号的均方误差结果最低,综合两段信号的测试结果,最终确定小波基取值为5 dB,并用于后续测试中。

采用本文方法对电压信号进行降噪处理,获取降噪后电压信号结果,并将降噪后的信号与降噪前进行对比,以验证本文方法的降噪效果,结果如图3所示。

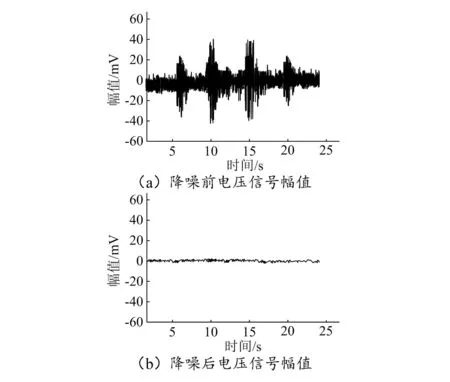
图3 降噪效果测试结果

由图可知,本文方法具备良好的降噪效果,能够完成电压信号中绝大部分噪声信号的去除,并且能够保留有效电压信号的完整性,去除噪声的电压信号没有发生信号中断和缺失现象。由此说明本文方法可以在保证电压有效信号完整性的基础上实现信号降噪。

采用本文方法对蓄电池短路故障进行检测时,需要计算序列元素之间的最短路径距离。这意味着最短路径距离的计算结果将决定故障检测结果的可靠性。为了评估本文方法在故障诊断方面的性能,获取了本文方法在第一次循环充电与其他各次循环之间路径距离的测试结果,如图4所示。

图4 路径最短距离测试结果

由图可知,随着充电循环次数增加,最短路径值也随之发生变化,前9次充电循环中,最短路径结果较低,9次之后,路径距离发生波动性变化,距离波动较大则表示在该循环充电下电压信号存在异常。因此,本文方法能够依据计算的距离判断电压的变化情况。

为了进一步评估本文方法在短路故障检测方面的效果,分别考虑了两种情况:序列长度相等和序列长度不相等。对前10次循环充电获取的信号进行检测,获取DTW的计算结果,如图5所示。

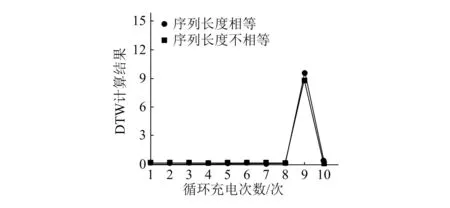
图5 短路故障检测结果

由图可知,两种序列长度下,本文方法均能够完成前10次循环充电电压信号的检测,并且在第9次时,检测出异常值。该结果表明本文方法检测性能良好,能够在序列长度存在差异的情况下完成故障的准确检测。

为直观体现本文方法的短路故障检测效果,采用本文方法对电压信号进行诊断,并获取信号序列的相似度值,以此判断本文方法的故障检测效果,测试结果如图6所示。

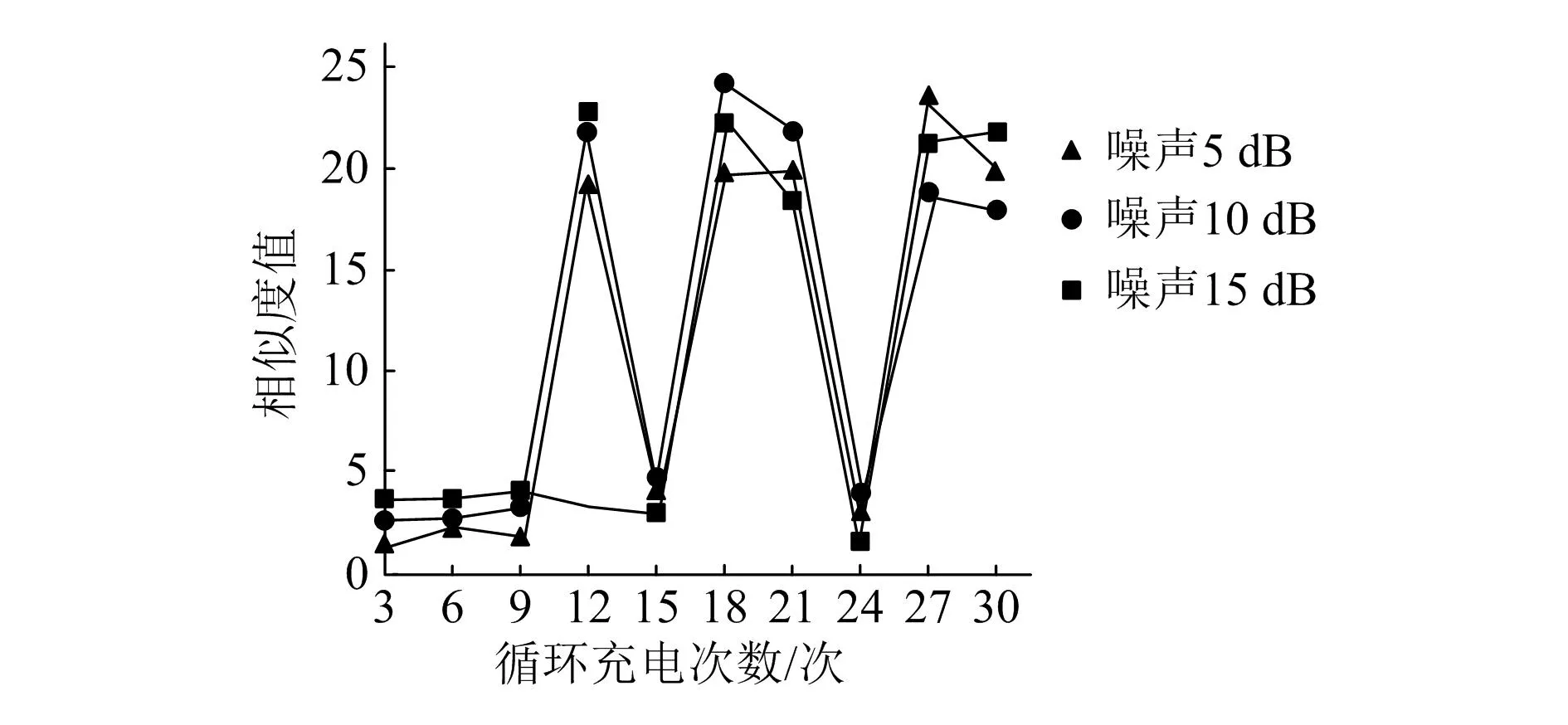
图6 相似度值测试结果

观察图6可知,使用本文方法计算出的6个相似度值之间存在较大差距,表示出现6次故障,该结果与实际结果一致。这是因为本文方法在进行短路故障检测时,综合考虑了信号降噪和不平衡时间序列处理,能够对序列数据集中的不平衡数据进行有效处理,因此能够依据蓄电池的电压信号可靠地检测出短路故障,并且不会受到噪声的影响。

3 结束语

综上所述,蓄电池若发生短路故障,可能会引发连带的电池故障,并给配电网造成严重损失。为了可靠地完成蓄电池系统的短路故障检测,本文提出了一种基于小波降噪的方法。该方法在配电网蓄电池系统短路故障检测方面进行了理论和实验验证,结果表明其具有较高的检测性能。本文方法在蓄电池系统短路故障检测时使用小波降噪技术,能够准确地检测到故障的发生。实验结果显示,在循环充电次数变化的情况下,本文方法的故障检测结果与实际结果一致,并且可以根据相似度值准确判断故障次数,这表明本文方法在实际应用中具有较强的实用性。