面向架空线路的作业机器人路径修正问题研究

毛益凉,邱 阳,郑敬禄

(浙江图盛输变电工程有限公司,浙江 温州 325025)

路径规划作为带电机器人智能控制的重要部分,其规划结果的优劣直接影响作业效率。因此,部分学者对机器人路径规划进行了大量研究,积累了大量经验,如闫冬等[1]提出层次深度强化学习的路径规划,使带电作业机器人实现了自主避障和自主导航功能;王杨等[2]为提高路径规划中坐标定位的精度,通过虚拟现实(virtual reality,VR)和增强现实(augmented reality,AR)技术对周边环境进行三维建模,以降低遮挡物对坐标定位的影响。带电机器人在架空线路检测作业中,会因为环境外力的影响使得架空线路出现一定程度的摆动,使得线路检测机器人实际运行轨迹与规划轨迹出现偏差。因此,对检测机器人运行轨迹进行偏差修正,对保证线路的正常检测尤为必要。关于轨迹偏差修正问题,谢龙光等[3]提出将模糊算法应用于路径跟踪,使预测路径的偏差矫正性能得以提高。虽然谢龙光对规划路径的偏差进行了修正,但主要侧重于路径跟踪。对于架空线路而言,小幅摆动是常见的问题。当小幅振动达到一定程度,会给检测机器人机械臂作业造成影响。由此,本文结合检测作业机器人机械臂运动学模型和路径规划算法,提出一种用于架空线路摇摆的路径补偿方法,并对该方法的可行性进行验证。

1 运动学建模

1.1 检测机械臂简图

本文选择应用于架空线路检测的三臂带电作业机器人为研究对象。该机器人在执行检测任务时,通过图1中机械臂上的X射线成像板对线路缺陷进行检测,其中机械臂包含3个转动关节和2个滑动关节,共5个自由度。通过控制这些关节的转动和滑动,即可调整末端执行器的空间位置与位姿,进而达到控制轨迹的目的。

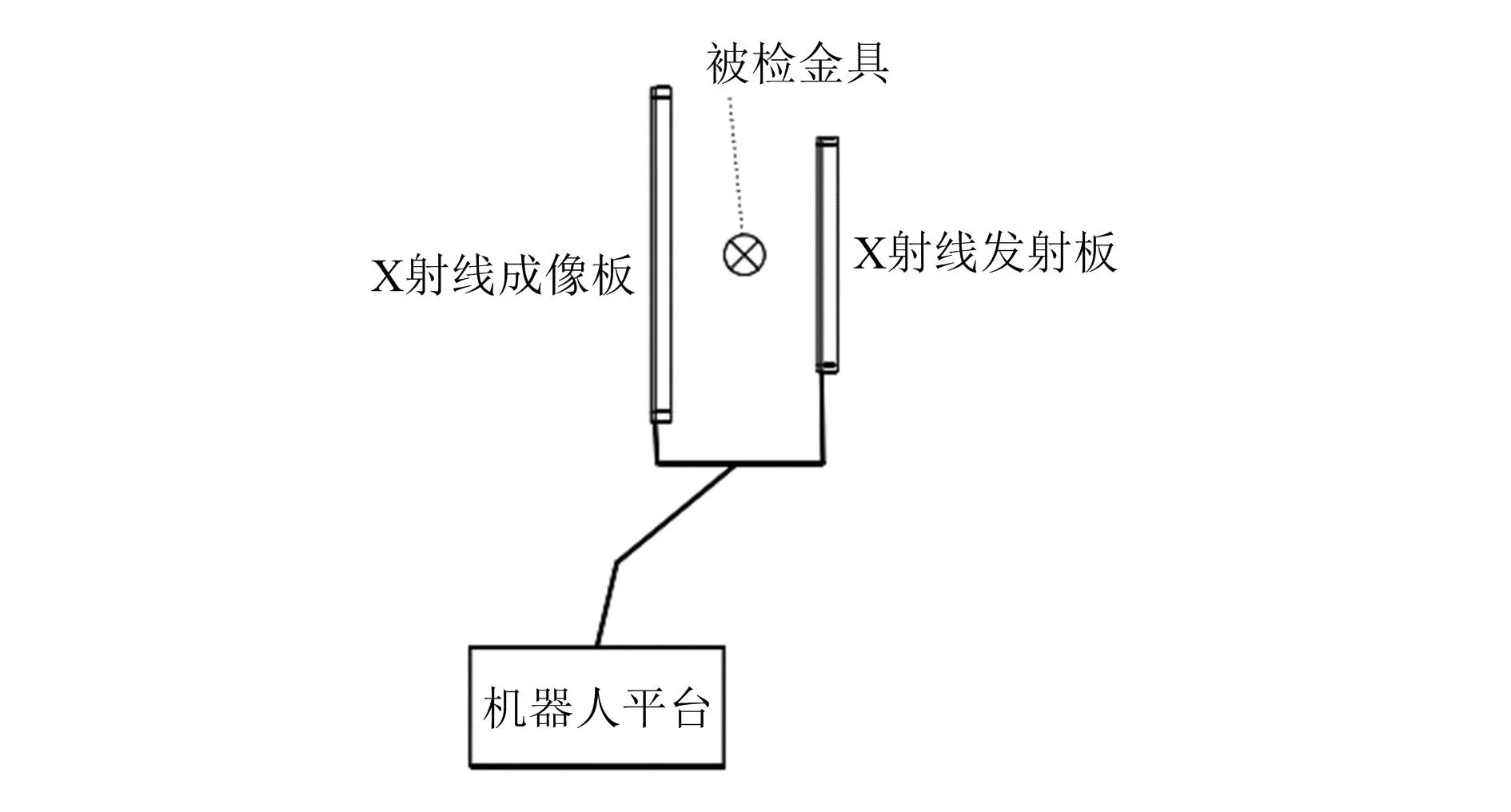
图1 检测臂示意图

1.2 运动坐标系构建

检测机械臂由连杆和关节组成,其运动学建模的本质即机械部件间的相对运动方程。为构建运动学方程,采用运动坐标系对连杆和关节在三维空间内的位置和位姿进行描述。具体通过D-H参数法构建机械臂运动坐标系,如图2所示[4-7]。

图2 检测机械臂的运动坐标系

图2中,Zi为第i个中心轴;Xi为垂直于Zi、与连杆中心线平行的坐标轴;θi为Xi轴与Xi+1轴的轴间角,也称转动关节变量;di为Xi轴、Xi+1轴在Zi+1轴上的映射距离,也称滑动关节变量。

由于D-H参数法构建的运动坐标系中滑动变量θi=0、转动惯量di=0,因此在图2中1、2、4关节的θi=0,3、5关节的di=0。

结合图2,对连杆和关节进行运动学分析,得相邻连杆的坐标转换公式为[8-9]:

(1)

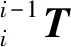
(2)

式中:M为机械臂关节总数。

联立式(1)、(2),得机械臂的正运动学方程:

(3)

其中:

(4)

关节变量的约束函数为:

(5)

通过坐标系转换法对式(3)中的各关节变量进行分离,得检测机械臂的逆运动学方程为:

(6)

式中:F(qi)表示关节i的目标位置,qi为机械臂关节变量值,ti表示qi单位变化所对应的时间。

2 路径规划

2.1 基于改进RRTstar算法的路径规划

考虑到多自由度机械臂实际作业中,每个关节和连杆的实际轨迹都会与规划轨迹出现偏差,且该偏差可以累积,因此选择基于改进RRTstar的路径规划算法对本文的机械臂进行路径规划更合适。结合改进RRTstar的基本原理,该路径规划步骤主要分为以下几步[10-11]:

1)从编号为0的节点开始,依次构建节点路径树Si,即节点能够到达的空间区域。

2)根据目标点位置,确定机械臂末端执行器(虚拟节点t+1)的位置Xt,从末端节点的路径树St中选出与Xt距离最近的点Xt-1。若Xt与Xt-1之间无障碍物,则Xt-1为规划的t节点的移动方向;若Xt与Xt-1之间存在障碍物,则将Xt-1从路径树中除去,重新选择与Xt距离最近的点,直至Xt与Xt-1之间无障碍物,记录Xt-1。

3)以Xt为圆心,以末端连杆长度at为半径,在路径树St中划分出一个圆形区域。连接Xt与Xt-2,设直线XtXt-2与圆形区域的交点为Yt-1,若XtYt-1小于XtXt-1,且XtYt-1与Xt之间无障碍物,则更新Xt-1为Yt-1。

4)根据规划出的节点位置,重复步骤2)和3),即完成对整个机械臂的路径规划。

2.2 规划轨迹的修正设计

改进RRTstar的路径规划考虑的是在没有任何外力影响的情况下,三臂机器人沿着架空线路进行运动。由于作业环境相对复杂,当机器人受到外力影响时(如风吹等),检测机器人的机身会出现摆动,如图3所示。

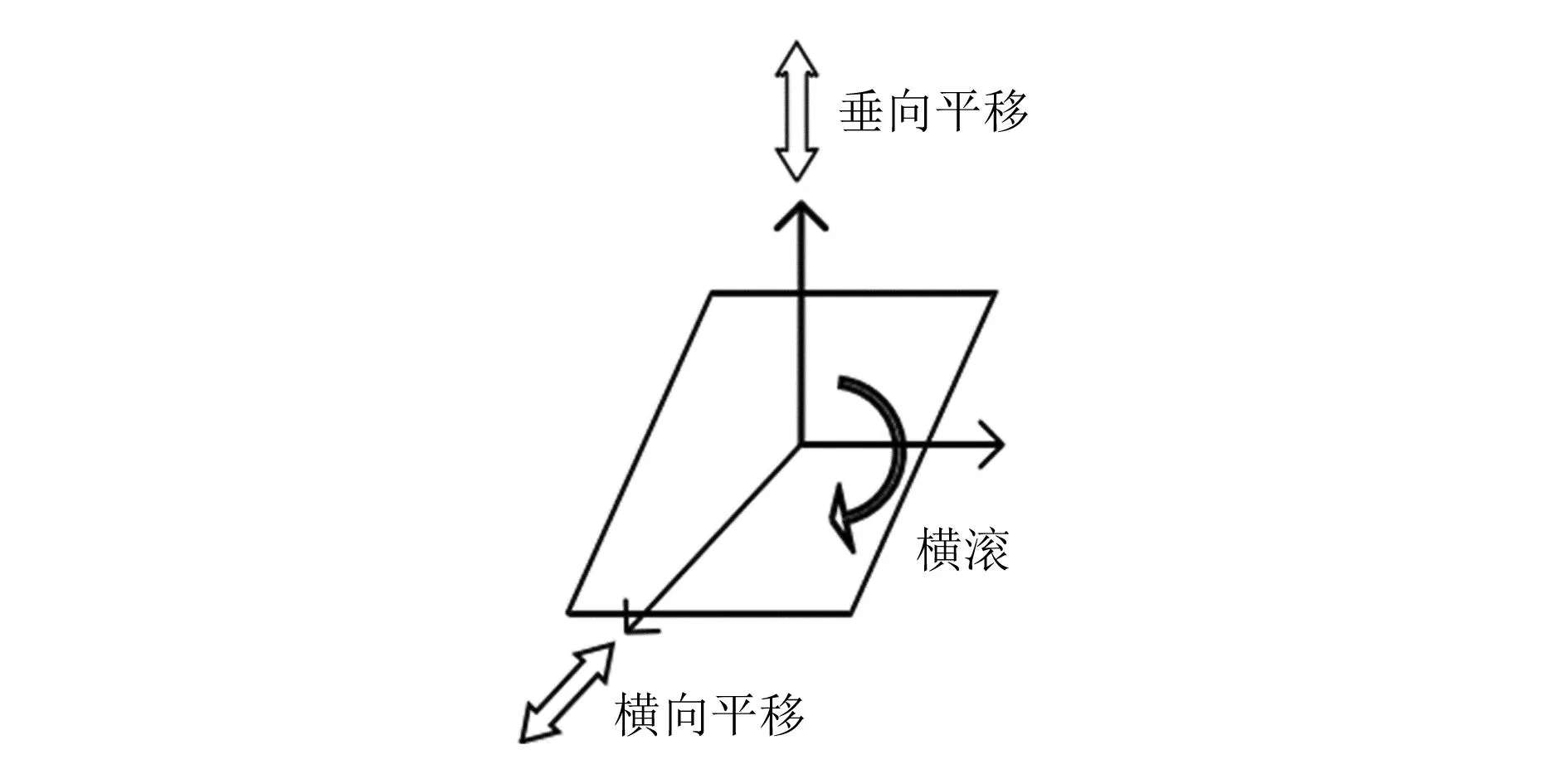
图3 机器人出现低幅摆动的简图

此时传统的改进RRTstar路径规划就不再适宜,所以需对路径进行适当修正。修正检测机器人路径的具体计算过程为:在地面建立坐标系G作为检测机器人作业的中心坐标系。在振动传感器位置建立坐标系S。当架空线路未发生摇摆时,G与S不存在相对位移。设机器人的水平移动惯量为ds,竖直移动惯量为dy,水平滚动惯量为θr。则G、S之间坐标系的转换矩阵可表示为[12]:

(7)

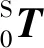
(8)

那么,G与0坐标系之间的转换矩阵可表示为:

(9)

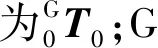
(10)

根据逆运动学方程求解式(9),可得矫正后的各个关节变量qi1,各关节变量补偿量Δqi为:

Δqi=qi1-qi0

(11)

式中:qi0为初始规划路径的关节变量,可直接调用。

通过设置阈值对求解出的qi0进行大小判断。当qi0小于阈值时,将计算出的补偿量加入路径规划算法中,对低幅摆动下的规划路径进行修正;当qi0大于阈值时,进行作业撤回的路径规划,使机械臂恢复原状。

以上路径修正的控制过程可用图4示意。

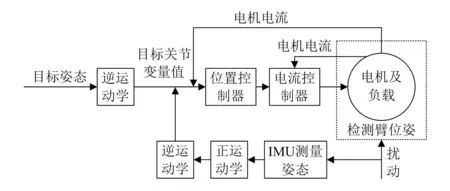
图4 路径规划修正过程示意图

3 试验验证

3.1 路径规划及修正验证

3.1.1试验环境及相关参数设定

选择在机器人操作系统(robot operating system, ROS)环境下进行三臂机器人建模。该机器人的初始位置和目标位置的三维模型如图5所示。

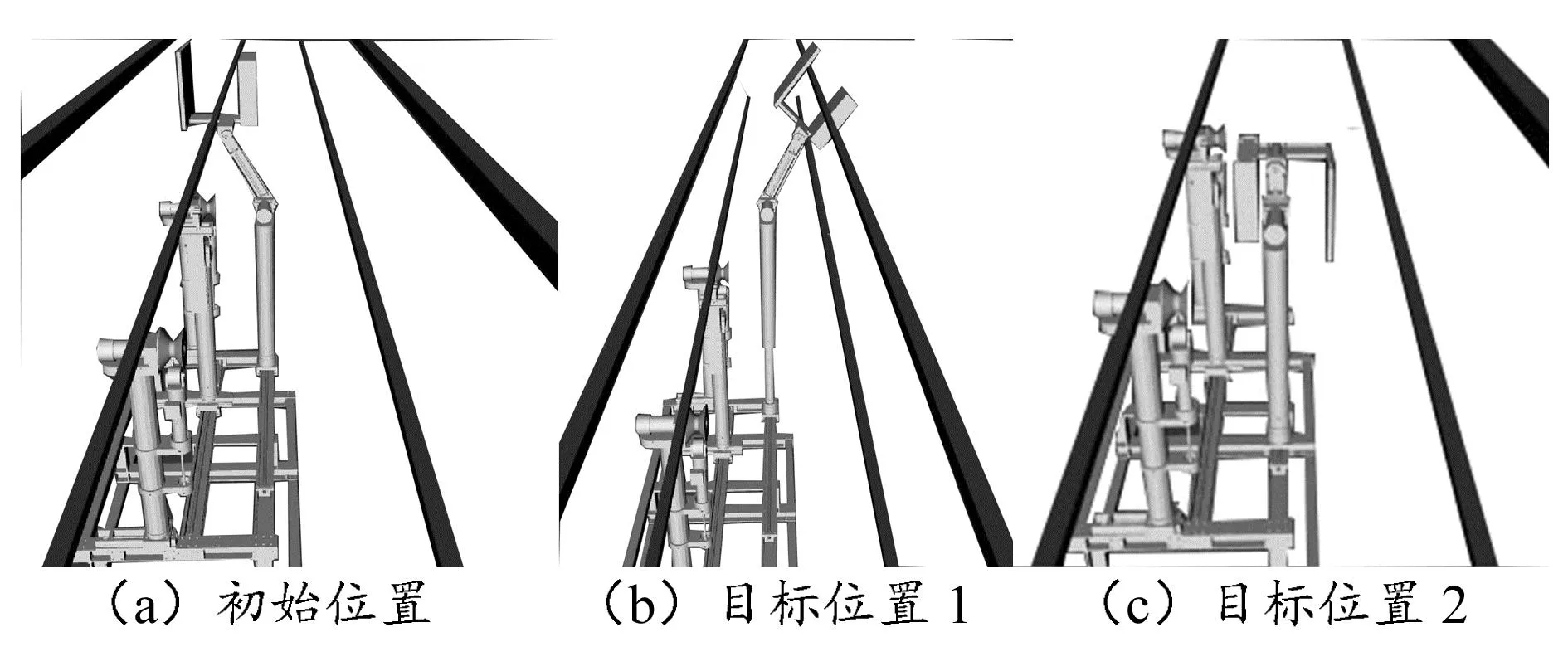
图5 机器人与架空线路的三维模型

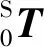
3.1.2路径规划算法性能验证

设Astar算法和改进RRTstar算法的最大迭代次数都为200次,在第1、2、3、4 s时记录执行结果。由此,得到两种算法对图5中的(a)→(b)和(b)→(c)的路径规划结果,具体见表1和表2。

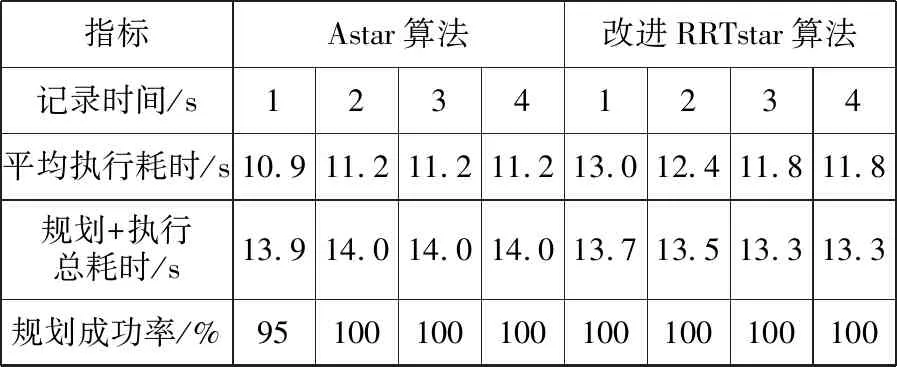
表1 (a)→(b)作业任务的路径规划结果

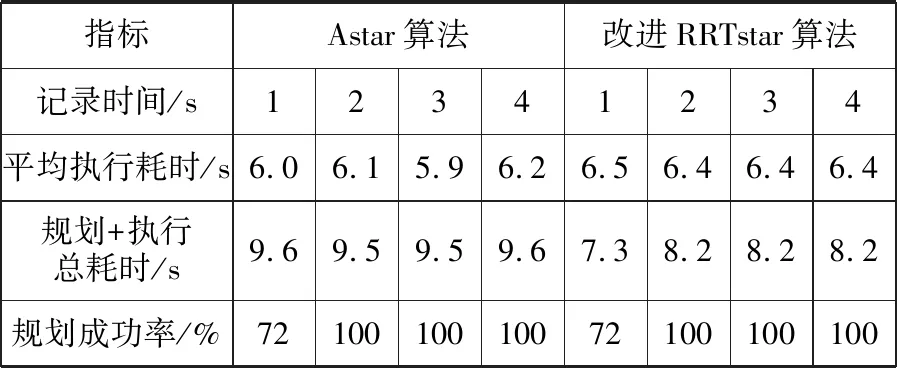
表2 (b)→(c)作业任务的路径规划结果

从表1可知,对于当前位置与目标位置间无障碍物的坐标任务,改进RRTstar算法的路径规划时间明显少于Astar算法。在1 s实现对机器人的路径规划,且规划成功率高达100%。从表2可知,对有障碍物的坐标任务,两种算法的路径规划能力有所降低。其中,Astar算法的路径规划时间超过3 s,改进RRTstar算法接近2 s;两种算法都成功躲避障碍物,且Astar算法规划的路径相比于改进RRTstar算法仍具有优势,但优势微弱;改进RRTstar算法执行有障碍物的坐标任务的作业时间较短,实时性较好。根据上述结果得出,改进RRTstar算法对机器人执行架空线路检测具有更强的路径规划能力,作业效率更高。

3.1.3路径规划修正算法验证

经试验可知,在Z轴方向上预测路径与目标路径的路径差异极小,因此可以不用修正。通过仿真,获得X轴、Y轴两个方向架空线路低幅摆动修正前后的路径规划结果,具体如图6所示。架空线路低幅摆动修正前后末端执行器连接的关节位置变化曲线如图7所示。

图6 修正前后的路径规划结果对比图

图7 修正前后末端执行器连接的关节位置变化曲线

从图6可知,导线低幅振动修正后,在X轴、Y轴方向的预测路径相较于改进前更为贴近目标路径,但仍有一部分路径与目标值存在偏差,这是因为修正计算过程存在一定误差。这类偏差对规划路径的整体影响极小,可忽略不计。

从图7可知,低幅振动修正后,规划路径距离约束边际相较于修正前更远,与架空线路产生摩擦的概率更低,机器人按照修正后的路径进行作业,安全性更高。

3.2 算法实际应用验证

3.2.1硬件搭建

为验证以上算法的实际应用效果,利用Jetson TX2平台搭建硬件平台,实现对路径的规划与修正,并通过Moveit工具实现对规划路径的插补。将插补后的规划路径通过串口通信方式发送至主控芯片,从而控制检测机器人按规划路径执行作业任务。

3.2.2路径规划总流程

结合图4和2.1节相关内容,加入修正的路径规划总流程如图8所示。其中,利用惯性测量单元IMU对姿态进行采集,利用改进RRTstar路径规划对机器人的路径轨迹进行修正补偿,实现姿态的修正。

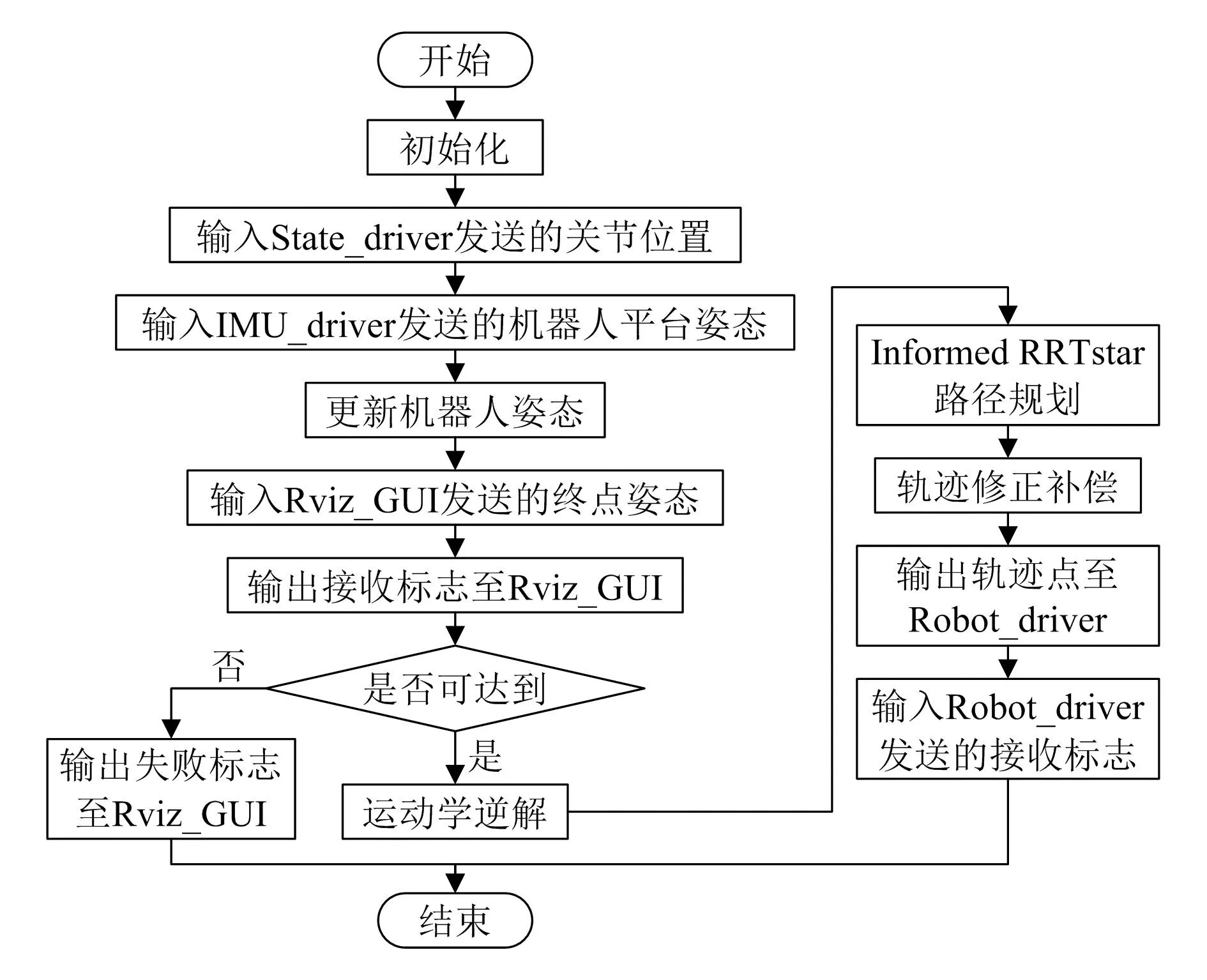
图8 路径规划总流程

3.2.3实际测试结果

机器人执行检测作业时,通过重力作用向机器人施加一定的低频振幅,从而得到路径修正前后机器人机械臂末端执行器的连接关节位置变化曲线,具体如图9所示。

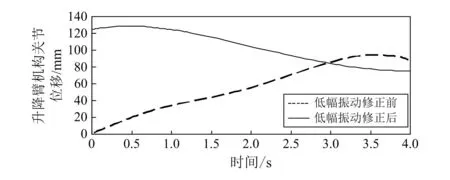
图9 修正前后末端执行器连接的关节位置实际变化曲线

从图9可知,在架空线路低幅摆动下,经过修正后的连接末端执行器的关节位置曲线更为平滑,且移动距离相对较短,说明具有更高的作业效率;修正后的路径距离约束边际相较于修正前更远,说明与架空线路产生摩擦的概率更低,安全性更高。

4 结束语

本文结合检测机器人的运动学模型和改进RRTstar算法,实现了低幅摇摆下的路径规划,证明该路径修正算法满足低幅振动的路径修正要求。但本文尚未针对大风等造成的高幅摆动提出解决方案,因此后续可从高幅摆动入手做进一步的探讨和研究。