大气湍流对高分辨率遥感卫星的成像影响研究
2024-02-05毛红敏丁致雅杨燕燕江苏奇彭建涛胡立发曹召良
毛红敏,丁致雅,杨燕燕,江苏奇,彭建涛,曹 楠,胡立发,曹召良
(1.苏州科技大学物理科学与技术学院,江苏 苏州 215009;2.江苏省微纳热流技术与能源应用重点实验室,江苏 苏州 215009;3.江南大学理学院,江苏 无锡 214122;4.中国航天科技集团公司上海卫星工程研究所,上海 201109)
1 引言
光学遥感卫星在地理探测、自然灾害预防、航空航天和军事等方面都发挥着重要作用。目前,高分辨率、甚高分辨率成为新一代光学遥感卫星的主流发展趋势[1-2]。各国都致力于研究大口径光学相机,以实现遥感卫星的高分辨率成像。但随着相机口径的增大,大气湍流对光波的干扰也随之增加[3-4],模糊、重影、畸变、光束漂移和闪烁等现象使遥感卫星的成像质量和定位精度受到影响。因此,研究大气湍流对遥感卫星成像质量的影响非常有必要。
目前,大气湍流对地基望远镜成像质量的影响已被广泛研究[5-6],并且以Kolmogorov 湍流理论为基础,建立了一套成熟的评价体系[7]。该体系可以定量分析评价大气湍流对望远镜成像质量的影响,进而用于自适应光学系统的设计和评估。但是目前关于大气湍流对空间相机成像的影响研究较少。地基望远镜观测空间目标时,目标距离地面非常远,此时目标发出的光可以近似看作平面波,其以柱状光束穿过大气湍流层进入望远镜。但是当遥感卫星对地面目标进行成像观测时,湍流层紧贴目标表面,目标发出的光则以锥状光束穿过大气湍流层,然后进入遥感光学相机。因此,针对地基望远镜的大气湍流影响规律无法直接应用到空间相机上。1966 年,Fried 首先针对此问题进行了研究[8],其以点光源发射的球面波传输模型分析了大气湍流对空间相机成像的影响,并推导出空对地观测时的位相结构函数,基于此,并结合Hufangel 和Stanley 的大气湍流折射率结构常数模型数据,假设相机口径无穷大,分析了最小地面分辨率和大气相干长度(r0)随海拔高度的变化[9]。阎吉祥等以平面波模型作为对象,通过计算到达角起伏,讨论了大气湍流对高空光学遥感系统地面图像分辨力的影响,发现在较强湍流时,高分辨力光学遥感系统需用自适应光学等方法进行湍流校正[10]。张晓芳等采用空-地观测时锥光(球面波)传输模型,针对不同的大气湍流折射率结构常数模型,对比分析了空-地和地-空观测时,大气相干长度的不同[11]。王仁礼等进一步研究了大气湍流对天基遥感系统成像分辨率的影响,其以r0=16 cm 的弱湍流为例进行分析,结果表明地面分辨率优于0.5 m 的高分辨率遥感成像需要考虑大气湍流因素[12]。陈欣欣等基于球面光波传输模型,以HV5/7 模型、合肥白天和夜间模型的大气湍流轮廓线仿真分析了大气湍流对空基成像系统分辨率的影响[13]。由于一个湍流轮廓线仅能描述一个固定的大气湍流强度,因此其仅分析了3 个固定湍流强度下空间相机的成像分辨率。
由上可知,研究者以球面波传输形式初步研究了遥感卫星对地观测时,大气湍流对卫星成像的影响。这些研究都是以几个固定的大气湍流强度为例,分析大气湍流对卫星成像分辨率的影响,没有得到任意大气湍流强度对遥感卫星成像影响的普适规律。为此,本论文针对该问题展开研究,基于空对地大气湍流传输模型,对湍流波前进行仿真,构建了大气湍流对遥感卫星成像影响的普适公式。本文研究可为高分辨率遥感卫星相机的设计和优化提供理论依据。
2 空对地大气湍流波前仿真
2.1 空对地大气湍流传输模型
大气湍流使光束在传播过程中发生波前畸变,导致光束产生漂移、闪烁和扩展等现象,对遥感卫星分辨率及探测精度产生影响。大气相干长度是表征湍流强度的参数,在地对空观测系统中其表示为[6,14]:
式中:h为大气层高度;β表示天顶角;z为海拔高度;k=2π/λ,其中λ表示光波波长;是大气湍流折射率结构常数。大气折射率结构常数用于表征湍流起伏强度,其不是常数,而是随着温度、风速、地理位置以及海拔高低的变化而变化。空对地观测模型如图1 所示。由于湍流层主要存在于距离地面30 km 以下,而卫星轨高通常大于150 km,因此卫星轨高变化时,大气湍流强度不发生变化。
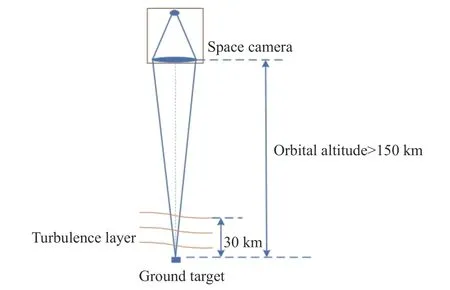
图1 卫星对地面目标探测示意图Fig.1 Schematic diagram of satellite detection to ground target
对于空对地观测系统,需建立如图1 所示的球面波模型,当受大气湍流干扰的球面波传输到遥感卫星相机入瞳处时,大气相干长度则表示为[8]:
式中H是卫星轨道高度。可以看出,是卫星轨道高度的函数,即卫星处于不同高度时,即使大气湍流强度相同,对应的值也不同,其描述的是大气湍流对遥感卫星光学相机的影响程度,而不代表大气湍流的强度。因此,对于空对地观测而言,大气湍流对卫星成像质量的影响与卫星的轨高有关。地面被测目标发出的球面波经湍流层被星载相机接收,当卫星高度增加时,相机对目标的张角减小,此时,光波经过的湍流区域减小,因此湍流的影响随之减弱。
若要利用公式(2)研究大气湍流对遥感卫星成像的影响,需要知道随海拔高度的分布情况。有多种分布模型[15],本文不考虑温度和风速的影响,重点讨论卫星处于不同轨道高度时成像质量受大气湍流的影响,故选择研究者广泛采用的Hufnagel-Valley 5/7 模型[16]:
依据HV 5/7 模型,大气折射率结构常数随海拔高度的变化规律如图2 所示。可以看出,高度低于5 km 时,数值大,湍流强;在5~30 km区间,湍流逐渐变弱;当高度超过30 km 时,湍流很弱不再考虑。因此,湍流对光波的影响主要集中于距地面高度30 km 以内。
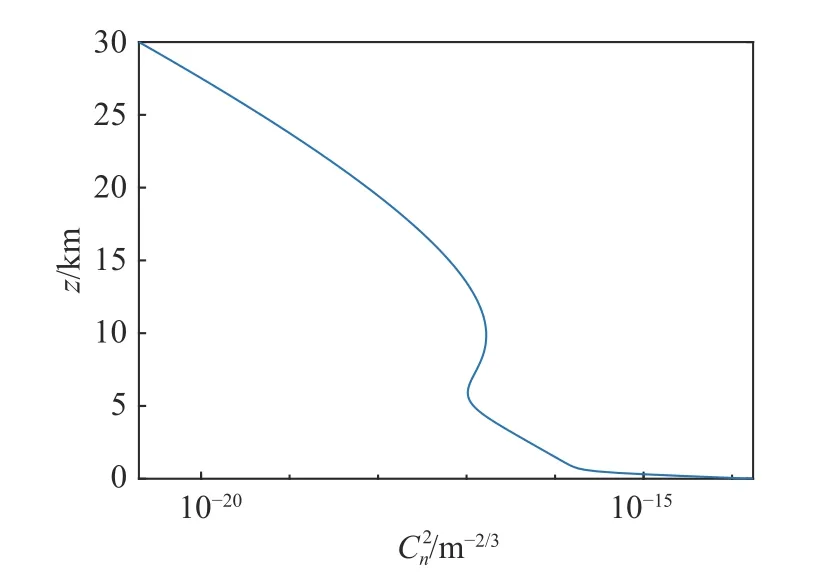
图2 折射率结构常数随高度z 的变化曲线Fig.2 Refractive index structure constant varying with height z
2.2 基于Zernike 多项式的湍流波前仿真
根据公式(3) 的大气折射率结构常数模型,可计算得到地对空大气相干长度r0和空对地大气相干长度的典型值,为讨论湍流强度变化提供参考。如轨高为150 km,计算得r0=5.56 cm,。此结果与张晓芳论文计算数据一致[11]。但是上述方法仅能够得到一个固定大气湍流强度,无法针对不同大气湍流强度进行仿真分析。为此,本文采用Noll 的基于Zernike 多项式的大气湍流仿真方法,以仿真不同湍流强度的畸变波前[17]。
湍流波前可用单位圆上正交完备的Zernike多项式来表示[17]:
其中:ai表示第i项Zernike 多项式的系数,Zi是第i项Zernike 多项式。利用Noll 描述湍流波前采用的Zernike 多项式[17]:
式中:odd 是全体奇数组成的集合;even 是全体偶数组成的集合;R表示极轴;θ为极角;n和m表示Zernike 多项式对应的径向级次和角向级次,n和m都为整数,且满足 0≤|m|≤n且 (n-|m|)为偶数。其中,可利用下式计算:
根据Kolmogorov 理论,湍流的位相结构函数可以表示为[17]:
式中r为径向变量,结合相位结构函数和Zernike 多项式,任意两项Zernike 多项式系数ai(ni,mi)和ai’(ni’,mi’)间存在时间相关性,其协方差可以表示为[18]:
由于实际空间的大气湍流是随机动态变化的,本文仿真过程中随机模拟100 幅波前,利用其统计平均值表示湍流波前。同时,本文采用惯用的工作波长λ=550 nm 进行仿真分析。图3(彩图见期刊电子版)是r0=5.56 cm、H=150 km、D=4 m时,仿真的湍流波前,其波面的 PV 值为1.28λ。

图3 仿真湍流波前Fig.3 Simulated turbulence wavefront
3 大气湍流对成像分辨率的影响
大气湍流产生的动态像差会严重影响遥感卫星的成像质量,且湍流波前的均方根(RMS)决定着大气湍流对遥感卫星的成像分辨率。为此,首先分析大气湍流对波前RMS 的影响规律,然后推导出其对卫星成像分辨率的影响公式。
3.1 大气湍流对波前RMS 的影响规律
依据空对地大气湍流仿真模型,可以得到不同大气湍流强度下的湍流波前,其RMS 值可由下式求出:
式中 φRMSi是一幅仿真湍流波前的RMS 值。本文中,N=100。同时,影响遥感卫星成像分辨率的参数有相机口径、卫星轨道高度和大气湍流相干长度,下面分别分析其对湍流波前RMS 的影响。
3.1.1 相机口径
为了分析相机口径和湍流波前RMS 的关系,选取r0=5.56 cm,卫星轨高H分别为150 km、350 km、550 km,仿真分析湍流波前随相机口径的变化情况,结果如图4 所示,其中离散点为仿真计算数据。可以看出,随着相机口径的增加,波前RMS 呈增大趋势。为了定量分析其变化规律,对仿真数据进行曲线拟合,连续线为拟合曲线。拟合结果显示,WRMS和D满足如下关系:
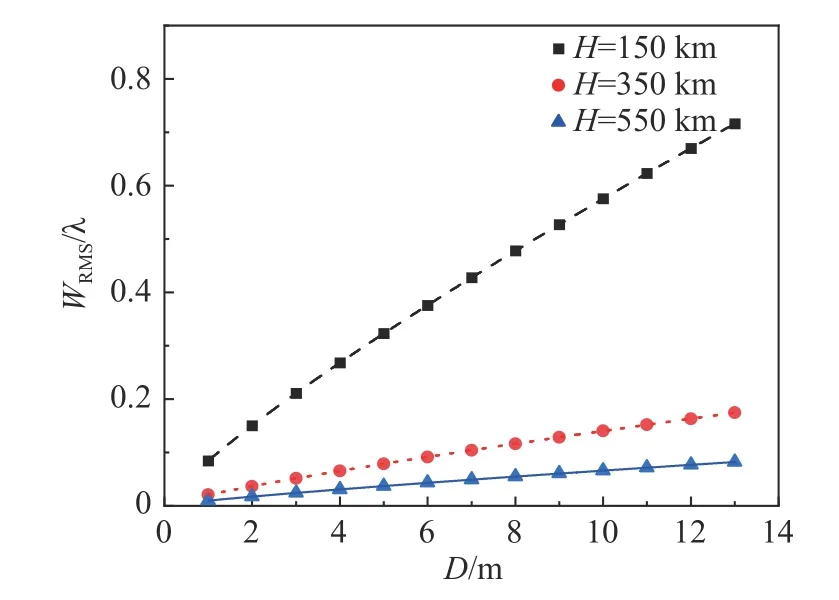
图4 相机口径D 对WRMS 的影响Fig.4 Influence of camera aperture D on WRMS
式中D的单位是m。卫星处于不同轨道高度时,系数a1具有不同的数值,H分别为150 km、350 km、550 km 时,有:a150km=0.08,a350km=0.02,a550km=0.01。公式(10)表明WRMS与D的5/6 次方呈线性变化。
3.1.2 卫星轨道高度
同样选取r0=5.56 cm 进行湍流波前的仿真分析。同时,设置D分别为4 m、6 m、8 m,仿真分析卫星轨高对湍流波前RMS 的影响规律,结果如图5 所示。
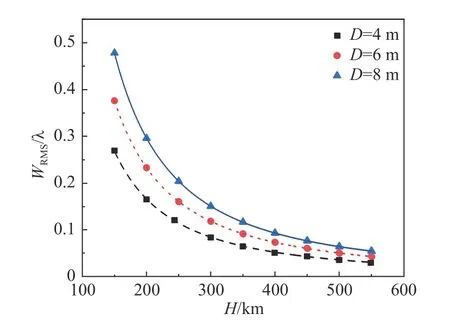
图5 卫星轨道高度H 对WRMS 的影响Fig.5 Influence of satellite orbital height H on WRMS
可以看出,随着轨道高度的增大,湍流的影响急剧减弱。采取和上节类似的方法,对仿真的离散点进行曲线拟合,获得湍流波前随卫星轨高的变化规律如式(11)所示:
式中H的单位是km。对于不同相机口径,系数a2也不同,对于D分别为4 m、6 m、8 m 时,其值分别为:a4m=1132.6,a6m=1592.1,a8m=2023.8,可以看出,WRMS与H的-5/3 次方呈线性变化规律,对于不同相机口径,仅系数不同。
3.1.3 大气相干长度
为了研究大气相干长度对湍流波前的影响,选取卫星轨高H=150 km,在D分别为8 m、6 m和4 m 时,仿真分析湍流波前随r0的变化规律,结果如图6 所示。可以看出,在不同相机口径下,湍流波前RMS 均随湍流的减弱而快速减小。同样对离散点进行曲线拟合,得到WRMS和r0的变化关系为:
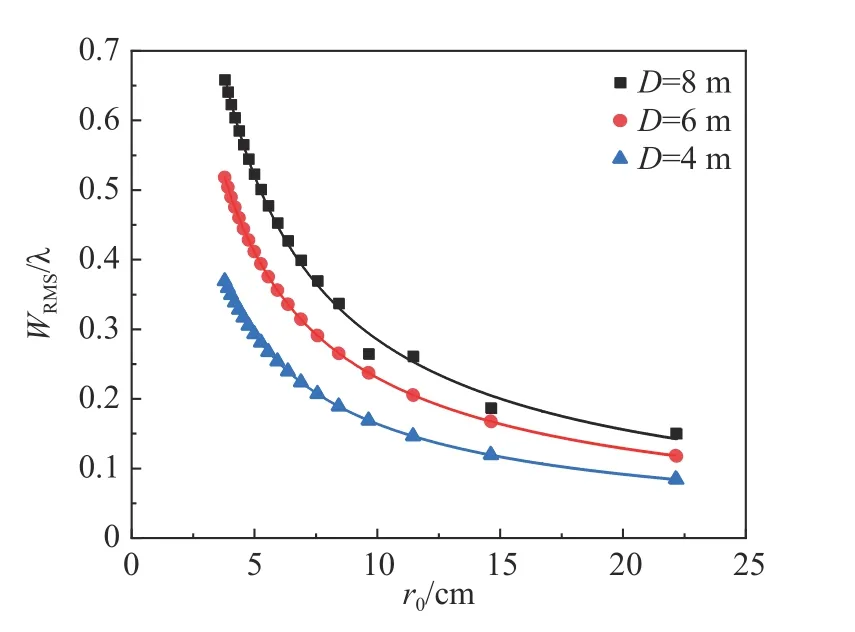
图6 大气相干长度r0 对WRMS 的影响Fig.6 Influence of atmospheric coherence length r0 on WRMS
式中r0的单位是m。可以看出,WRMS与r0的-5/6次方呈线性变化。对于不同相机口径,仅仅是系数a3的值不同。对于D分别为8 m、6 m 和4 m时,a3的值分别为:a8m=0.043,a6m=0.034,a4m=0.024。
3.1.4 规律归纳
式(10)~式(12)分别给出了湍流波前RMS随D、H、r0的变化规律。为了得到湍流波前随D、H、r0变化的统一规律,须对式(10)~式(12)进行进一步分析归纳。其可以统一写成如下形式:
式中A是系数,如果能够求解出A,便可以得到湍流波前的RMS 随D、H、r0的统一变化规律。为此,根据公式(13),可以把式(10)~式(12)进行重写。对于r0=5.56 cm、H=150 km,公式(10)可重写为:
对于r0=5.56 cm、D=8 m,公式(11)可重写为:
对于H=150 km、D=8 m,公式(12)可重写为:
再结合曲线拟合时得到的系数a1,a2,a3,可求出系数A1=31.86、A2=32.36、A3=32.18。可以看出,3 个值都接近32,因此取A=32。此时,湍流波前随D、H、r0的变化规律可以表示为:
式中,D和r0的单位是m,H的单位是km,WRMS的单位是波长λ。
为了验证公式(17)的有效性,令公式(17)中的3 个变量D、r0、H随机选取不同值,然后利用式(17)计算出理论波前RMS 值;再依据选取的参数进行湍流波前仿真,获得波前RMS 的仿真值;将二者进行比较,以确认该公式是否有效。
随机选取3 个变量的8 组数值,如表1 所示。仿真和理论计算结果如图7 所示。从图7(a)可以看出,理论值和仿真值非常接近。为了定量分析理论公式的有效性,计算了仿真值和理论值的相对误差,结果如图7(b) 所示。其平均相对偏差为0.6%,最大相对偏差为0.7%,说明公式(17)可用于计算任意条件下湍流波前的RMS 值,因此具备普适性。
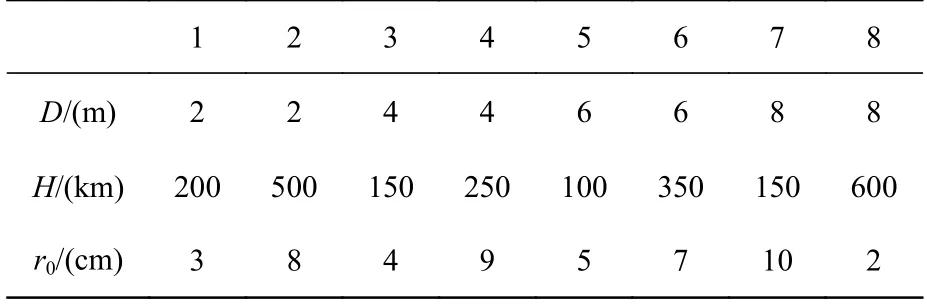
表1 随机选取的变量Tab.1 Randomly selected variables
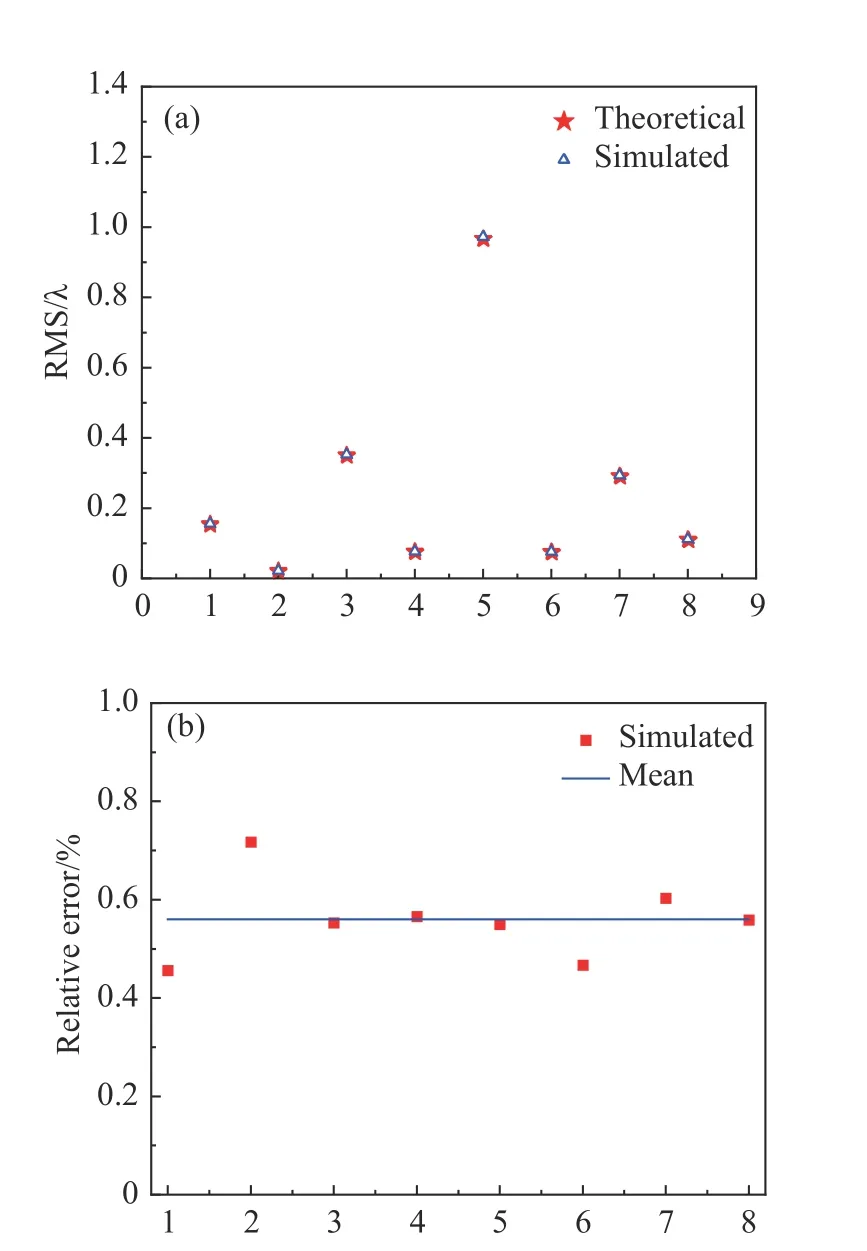
图7 (a) 不同参量值下的仿真值与理论值及(b)仿真值与理论值的相对误差Fig.7 (a) Simulated and theoretical values under different parameters;(b) relative error for simulated and theoretical values
由公式(17)便可以求解出任意条件下,大气湍流对空间相机波前RMS 的影响,结果如图8(彩图见期刊电子版)所示。
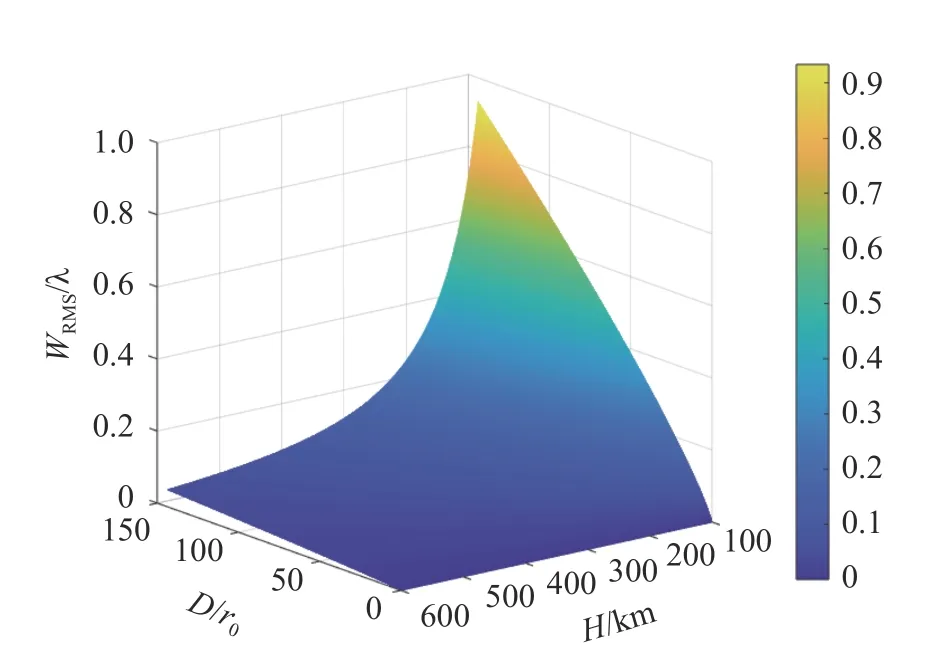
图8 波前均方根随大气湍流强度和卫星高度的变化规律Fig.8 Variation of root mean square of wavefront with atmospheric turbulence intensity and satellite altitude
通常也可以用D/r0来表示湍流的强度,可以看出,湍流强度越强、轨高越低,湍流波前的RMS 值越大。因此,可以利用式(17)的湍流变化普适规律,来评估湍流对空间相机波前的影响,从而为分析其成像分辨率提供依据。
3.2 大气湍流对成像分辨率的影响
为了分析大气湍流对空间相机成像分辨率的影响,需要建立湍流波前RMS 值和成像分辨率的关系。而湍流波前和斯特列尔比S之间的关系可以表示为[19]:
由湍流波前可以求出系统的斯特列尔比。而光学系统的角分辨率θ和S有如下关系[20]:
因此,利用式(17)~式(19),便可以求出大气湍流对空间相机成像分辨率的影响。此外,其线分辨率可由下式求出:
为此,由式(17)~式(19),即可得到空间相机的成像分辨率公式:
该公式是评估大气湍流对空间相机角分辨率影响的普适公式,利用其可以求出任意条件下空间相机的角分辨率。图9(彩图见期刊电子版)是在r0=5.56 cm、λ=550 nm 时,角分辨率随轨道高度和相机口径的三维空间分布。可以看出,卫星轨高越低、口径越小时,角分辨率 θ越大,表明分辨能力越差。
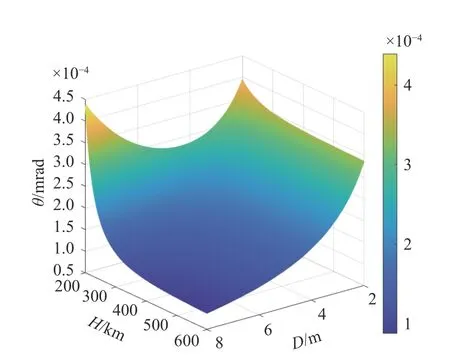
图9 角分辨率随卫星高度和相机口径的变化规律Fig.9 Variation of angular resolution with satellite altitude and camera aperture
根据公式(20),线分辨率可以表示为:
当λ=550 nm,D=4 m,r0=5.56 cm 时,遥感相机的线分辨率随卫星轨高的变化规律如图10 所示。同时,为了对比分析大气湍流的影响,也给出了理想情况下线分辨率随卫星轨高的变化曲线,如图中实线所示。可以看出:当没有大气湍流时,线分辨率随卫星轨高呈线性变化趋势;当存在大气湍流时,线分辨率随卫星轨高先逐渐减小,然后又逐渐增大,在轨高为240 km 处最小,即线分辨能力最强。同时,当卫星轨高在大约600 km时,两条曲线近似重合,说明此时大气湍流对遥感卫星的分辨率几乎没有影响。综上所述,大气湍流对遥感卫星成像分辨率的影响,与卫星轨高紧密相关。
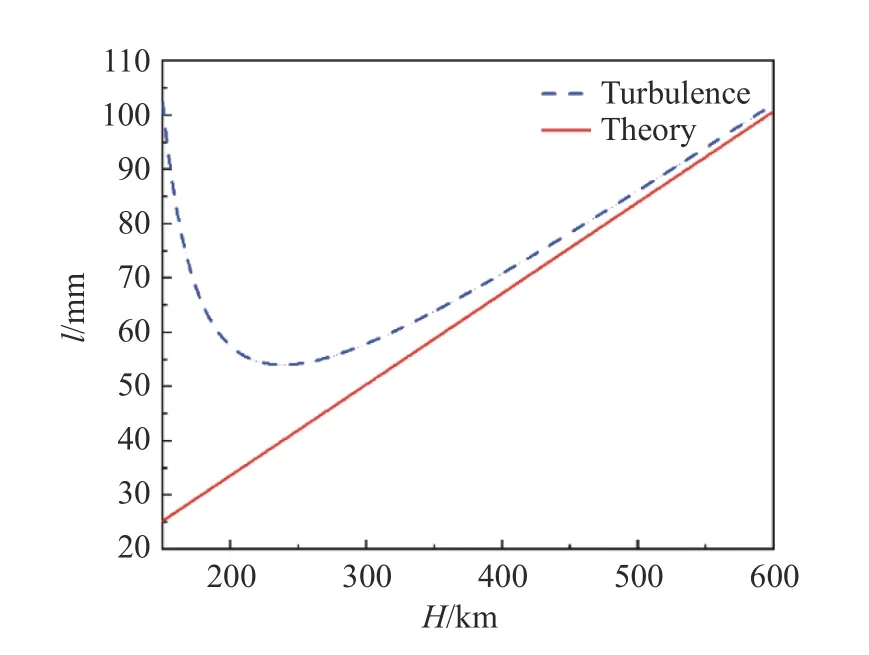
图10 线分辨率随卫星高度的变化规律Fig.10 Variation of line resolution with satellite altitude
为了验证上述线分辨率仿真的可靠性,把图10 的结果和文献[8]中的图2 和图3 结果进行对比分析。文献[8]的图3 给出了大气相干长度随卫星轨高的变化规律,结合该文献中的计算公式可以得出,当卫星轨高为680 km 时,其r0=4 m。本文图10 显示,当卫星轨高为600 km时,两条曲线重合,此时,大气湍流对4 m 口径光学相机的成像分辨率无影响。这说明,此时大气相干长度等于相机的光学口径,即r0=4 m。因此,本文的结果和文献[8]中的图3 结果都表明:当卫星轨高为680 km 时,r0=4 m。两者相互印证。
文献[8]中的图2 给出了最小线分辨率随卫星轨高的变化情况。该结果的前提条件是,在不同海拔高度处,空间相机的口径都大于等于大气相干长度,或者说空间相机的口径为无穷大。在此前提条件下,当空间相机的高度大于大气层高度时,最小分辨率为定值,不再随卫星轨高的变化而变化。因此,对于4 m 口径的空间相机,为了和文献[8]的图2 进行对比,需要满足r0≤D。取r0=D=4 m,其对应的卫星轨高H=600 km。由图10 可知,在H=600 km 时,其线分辨率约为10 cm。文献[8]在其讨论部分给出的最小线分辨率δl0也是10 cm。因此,该结果也说明本文图10 的仿真结果有效。
4 大气湍流对空间相机调制传递函数的影响
光瞳函数可表示为:
式中φ(x,y)是波前相位分布,A(x,y)是孔径函数:
光学传递函数(OTF)是光瞳函数的自相关:
利用OTF 的振幅部分即可得到调制传递函数MTF 。因此,如果已知光瞳函数便可以得到系统的MTF。在光瞳函数中,孔径函数和相机的口径相关,相机一旦确定,其便是已知量。由此可知,如果能够获得波前相位分布φ,便可以求出相机的MTF。而大气湍流产生的畸变波前φ可以利用文中的湍流仿真方法获得,因而可以进行大气湍流对相机MTF 的影响分析。
为分析大气湍流对MTF 的影响,也同样随机产生100 幅湍流波前,并利用式(23)~式(25)获得100 组MTF 曲线,同时进行统计平均,获得平均MTF 曲线。例如,对于r0=5.56 cm、H=150 km、D=6 m,其x方向MTF 曲线如图11 所示,实线为100 幅随机湍流对应的MTF 曲线,虚线为系统的理论MTF0曲线,■代表MTF 的统计平均值。
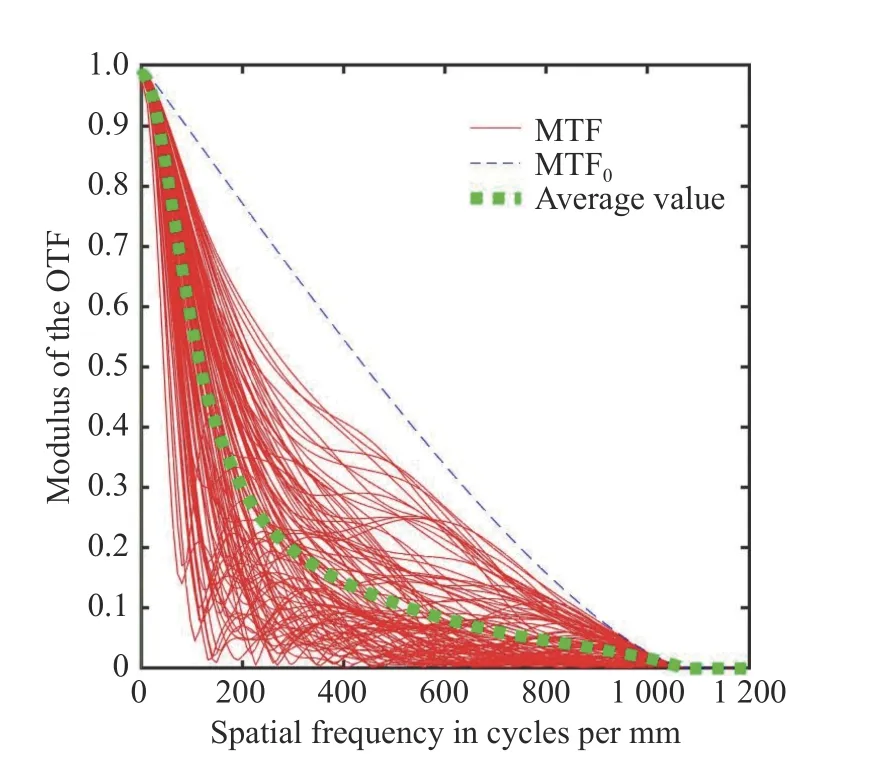
图11 100 组湍流波前在x 方向的MTF 曲线Fig.11 MTF curves of 100 sets of turbulent wavefronts in the x-direction
利用上述方法,分别仿真分析了卫星轨高、相机口径和大气相干长度对相机MTF 的影响,结果如图12 所示。图12(a)中,r0=5.56 cm、D=6 m,对应的虚线、点线和实线分别表示H=150 km、350 km、550 km 时的MTF 曲线。可以看出,随着卫星轨高的增大,相机的传函明显变好,并逐渐接近理想传函。图12(b)中,r0=5.56 cm、H=350 km,对应的实线、点线和虚线分别表示D=4 m、6 m和8 m 时的MTF 曲线。可以看出,随着相机口径的增加,曲线下方的面积有所减小,但变化不明显,表明在大气湍流影响下,光学口径已经不是影响MTF 的主要因素。图12(c)中,D=8 m、H=150 km,对应的虚线、点线和实线点线分别表示r0=3.91 cm、6.36 cm 和14.61 cm 时的MTF 曲线。可以看出大气相干长度越小,即湍流越强,则曲线下所包围的面积越小,系统传函明显变差。
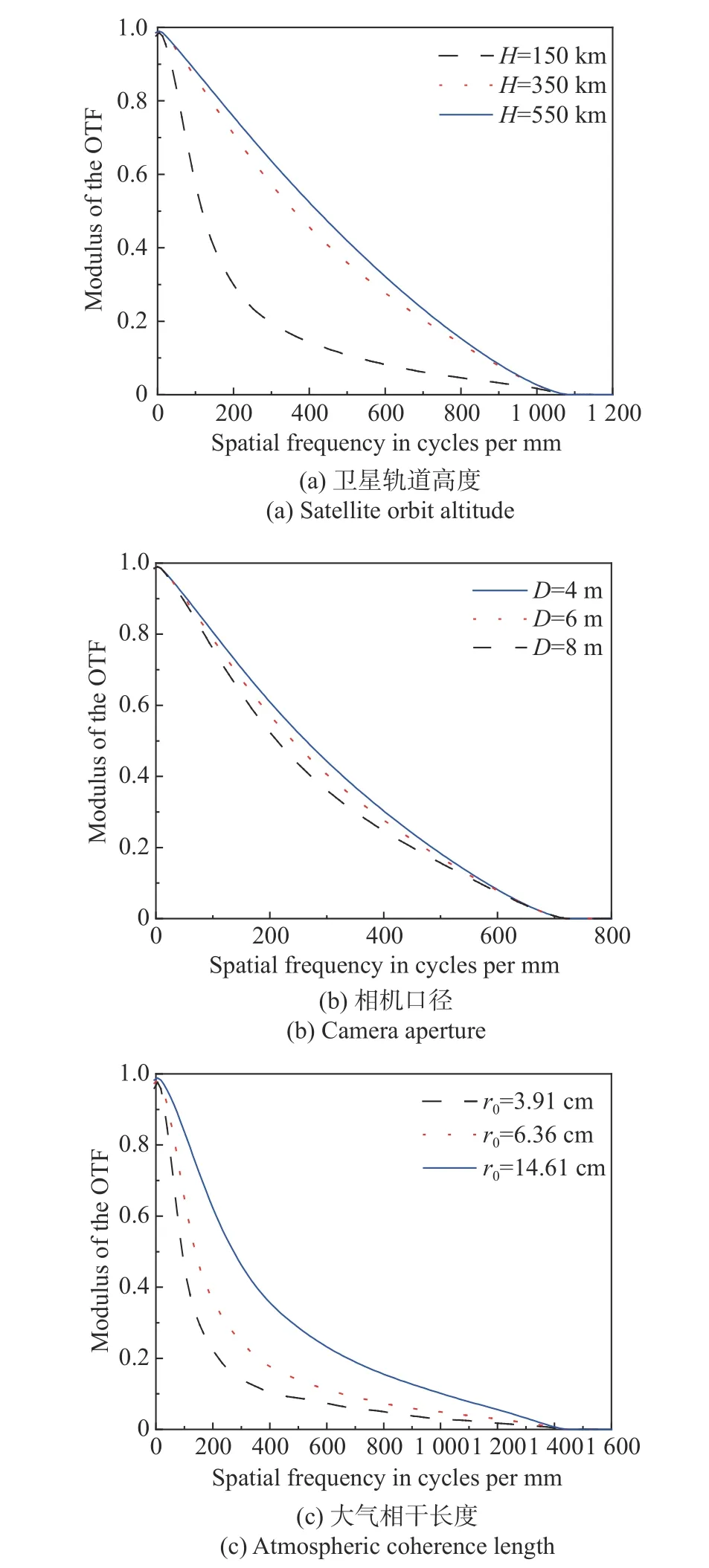
图12 调制传递函数随不同参数的变化曲线Fig.12 Curve of modulation transfer function varying with different parameters
在设计遥感相机时,通常以MTF 值等于0.15时对应的空间频率作为相机的最高分辨率。为了分析大气湍流对MTF 的影响程度,引入MTF 相对误差 Δ:
式中f0为理想情况下系统MTF 等于0.15 时对应的空间频率,f为受大气湍流影响时MTF 等于0.15对应的空间频率。Δ 越小,表明光学系统受湍流的影响越弱,成像质量越高。利用该评价指标仿真分析MTF 的相对误差Δ 随相机口径、卫星轨高和大气相干长度的变化规律,结果如图13 所示。
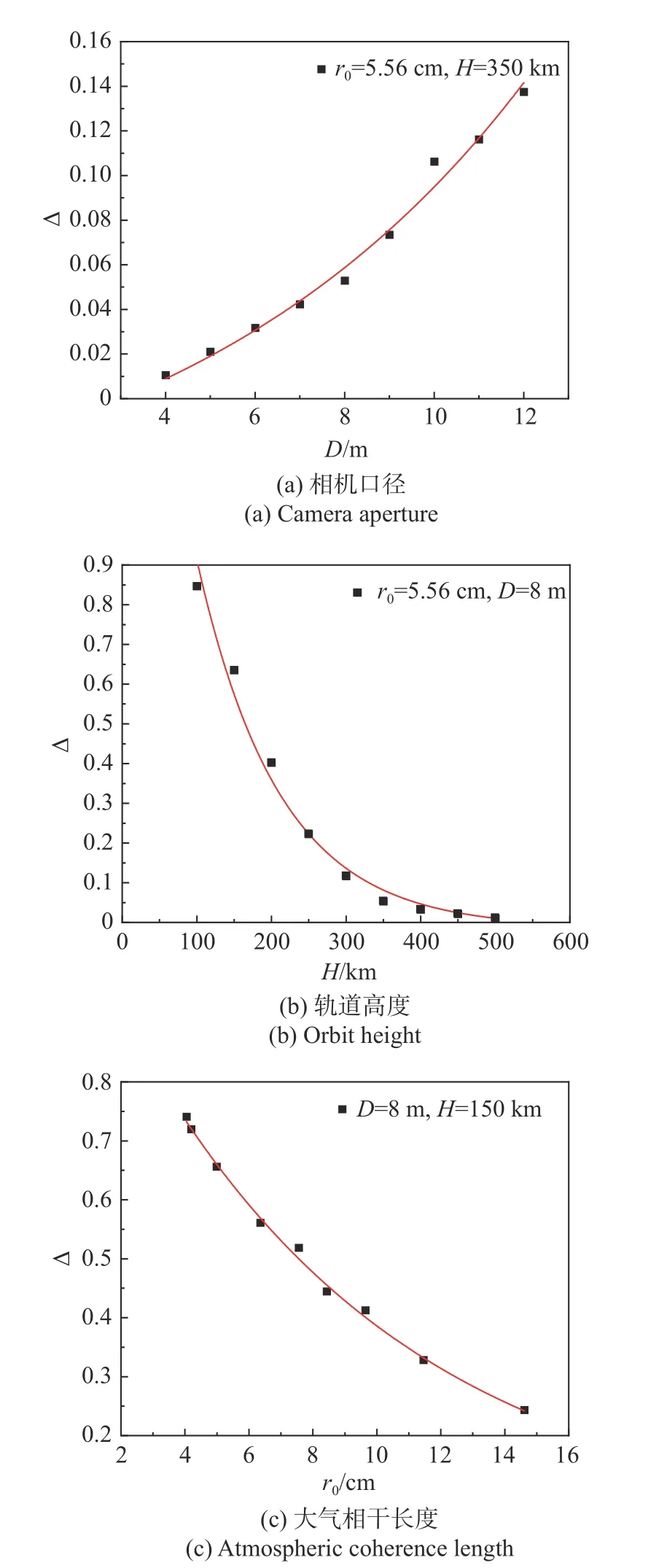
图13 MTF 相对误差随不同参数的变化规律Fig.13 Variation of relative deviation of MTF with different parameters
图13(a)为r0=5.56 cm、H=350 km 时,相对误差随相机口径的变化曲线,离散值为仿真结果,实线为拟合曲线。结果显示,随着相机口径的增大,MTF 的相对误差也增大。但是其相对误差较小,当口径在10 m 以内时,相对误差都小于10%。说明在该湍流强度下,当卫星轨高为350 km 时,相机口径对MTF 的影响较小。根据拟合结果,MTF 的相对偏差可以表示为:
说明MTF 的相对误差Δ 随相机口径D呈e 指数变化。
图13(b)是在r0=5.56 cm、D=8 m 时,MTF 相对误差随卫星轨高的变化情况。可以看出,随着卫星轨高的变大,大气湍流对相机传函的影响减弱。但是在轨道较低时,湍流对MTF 的影响较大。曲线拟合结果显示,MTF 的相对误差随卫星轨高的变化情况可表示为:
可以看出,MTF 的相对误差Δ随卫星轨高H呈e 负指数变化。
图13(c)为D=8 m、H=150 km 时,MTF 相对误差随大气相干长度变化的结果。仿真结果显示,随着大气相干长度的增大,即大气湍流的减弱,MTF 的相对误差也逐渐减小。但是,即使在弱湍流下,当卫星轨高较低时,湍流对相机MTF 的影响依然较大。曲线拟合得到MTF 的相对误差与大气相干长度的关系为:
可以看出,MTF 的相对误差Δ 随大气相干长度r0也呈e 负指数变化。
从上述仿真结果可以看出,MTF 的相对误差Δ 随相机口径D呈e 指数变化,随卫星轨高H、大气相干长度r0则呈e 负指数变化。实际空间相机设计中,可依据这些变化规律评估遥感卫星的成像质量。
5 结论
本文研究了遥感卫星对地观测时,大气湍流对其成像质量的影响。首先,基于Kolmogorov 大气湍流理论,以球面波传输方式建立遥感卫星的空对地大气湍流仿真模型,以实现大气湍流畸变波前的模拟仿真。然后,利用空对地大气湍流仿真模型,仿真分析卫星轨高、相机口径和大气相干长度对湍流波前RMS 的影响,并归纳建立了三个变量随机变化时湍流波前RMS 值的普适公式。接着,基于该普适公式给出了大气湍流对空间相机分辨率的普适影响规律。结果显示,成像分辨率随卫星轨高的增加先逐渐减小,然后又逐渐增大,并在拐点处(240 km)达到最高线分辨能力。同时在卫星轨高大于600 km 时,理想曲线和湍流影响曲线近似重合,说明此时大气湍流对遥感卫星的分辨率几乎没有影响。最后,研究了大气湍流对空间相机MTF 的影响,建立了MTF 相对误差的评价方法。仿真结果显示,MTF 的相对误差随相机口径呈e 指数变化,随卫星轨高、大气相干长度则呈e 负指数变化。
本文得到的大气湍流对遥感卫星成像分辨率影响的普适规律和公式,可为高分辨率遥感卫星的设计、分析和应用提供理论依据,进一步推动大口径空间相机在遥感卫星上的应用。
