基于虚拟坐标的矢量地图差值扩展可逆水印方法

戴 千 一,吴 柏 燕

(湖南科技大学地理空间信息技术国家地方联合工程实验室,湖南 湘潭 411201;湖南科技大学测绘遥感信息工程湖南省重点实验室,湖南 湘潭 411201;湖南科技大学地球科学与空间信息工程学院,湖南 湘潭 411201)

0 引言

数据安全是城市数字治理的重要前提,数字成果的应用与共享应以数据安全为基础。数字水印技术能弥补传统加密技术限制共享的局限性,在嵌入水印的同时保留原始载体的使用价值[1-3],而在医学诊断、军事地图和遥感测绘等特殊场合需要使用无损的高精度数据,可逆数字水印应运而生。可逆水印技术可在正确提取水印的同时无损恢复原始载体数据,避免数据永久失真[4]。目前栅格图像的可逆水印算法较成熟,主要包括基于无损压缩[5]、直方图平移[6,7]和差值扩展[8,9]3种算法,而矢量数据高精度和低冗余的特性使得水印嵌入条件更严格,故栅格图像的水印算法不完全适用于矢量数据[10]。

国内外针对矢量数据可逆水印的研究大多借鉴图像水印算法。基于无损压缩,Celik等[5]提出一种高容量低失真的广义无损LSB水印嵌入算法,比传统 LSB 方法具有更大的灵活性和更精细的容量失真粒度。基于直方图平移,Chen等[7]整合3类直方图(像素灰度直方图、差值直方图和预测误差直方图)平移的优势,采用基于块的多轮预测提高了图像质量和水印容量。相比无损压缩和直方图平移技术,差值扩展技术具有计算复杂度低和易获得高水印容量的优势,如Wang等[11]首次将差值扩展技术用于矢量地图数据水印,提出基于地图坐标和曼哈顿距离的两种水印嵌入方案,但因方案水印容量低,顶点相关性低的地图在水印嵌入后失真明显。为平衡水印容量和图形质量,周璐等[12]基于相邻顶点构建坐标差值直方图,利用差值扩展嵌入水印,在相同精度容忍度下取得了更高的水印容量和图形质量,但地图水印容量最高仅为0.5 bit/点。随后,Peng等[13]改进差值扩展技术,将水印嵌入二维CAD工程图所有顶点相对坐标的比率集上,提高了水印容量和不可感知性,但若参考顶点逆序提取水印则会破坏水印数据完整性。以上研究均为差值扩展技术在矢量数据水印上的应用,嵌入水印时均重点关注水印容量和图形质量。此外,部分学者从可逆性与鲁棒性入手提升水印性能。例如:Cao等[14]从载体数据入手增强水印可逆性,使用Douglas-Peucker算法提取矢量地图特征点,将非线性加扰后的特征点和非特征点作为载体嵌入水印,算法严格可逆且对地图简化攻击鲁棒;佟德宇等[15]提出一种结合水印区间定位和区间内部定位的双重映射机制,同时对区间内部定位和水印值进行校验,将校验后的水印信息嵌入坐标的可嵌入位中,增强了算法鲁棒性;任娜等[16]基于脆弱水印技术提出通过坐标重排序重新建立空间关系,将当前要素所生成的水印信息量化嵌入其他要素中,从而有效避免了要素删除导致水印信息一同删除的问题;唐伟[17]提出一种适用于矢量瓦片数据的大容量鲁棒水印方法:在水印生成阶段,分段生成代表组编码和用户编码的水印信息,进一步提高水印检测的正确性,在水印嵌入阶段,对经典QIM水印嵌入方法进行改进,划分出更多数量区间,水印容量大幅提升;奚旭等[18]为弥补水印容量提升使水印不可见性降低的缺陷,提出量化索引调制坐标点状态值嵌入水印,采用MPR(Maximum Perturbation Regions)方法限定坐标范围以控制水印隐蔽性,该方法水印容量大且数据扰动程度可控,但算法整体计算复杂度较高。

综上可知,目前矢量数据可逆水印研究聚焦于水印容量和数据失真问题[13,19-22],水印可逆性和不可见性仍是衡量可逆水印算法性能的重要指标,如何保持水印容量、水印不可见性及数据质量的良好平衡是当前研究的重点和难点。传统差值扩展技术应用于顶点相关性低的矢量地图时,水印容量较低,数据失真明显,导致水印效果不理想。因此,本文提出一种新的矢量地图差值扩展可逆水印方法,即将虚拟坐标融入差值扩展技术,将水印嵌入差值直方图平移后的差值中,以解决传统差值扩展技术应用于矢量地图可逆水印时容量不足及数据失真问题。

1 基于虚拟坐标的改进差值扩展技术

1.1 基于虚拟坐标的差值计算

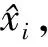
(1)

图1 虚拟坐标构建差值示意

(2)

(3)

(4)

1.2 参考坐标标识图

理论上虚拟坐标与实际顶点重合时,在提取水印时易造成参考坐标判断错误,从而导致无法正确提取水印,故仅对不与虚拟坐标重合的顶点嵌入水印。提取水印时,差值计算所基于的参考坐标与水印嵌入时应保持同步,因此在水印嵌入阶段记录每个实际顶点的参考坐标,称为参考坐标标识图,记为L={b1,b2,…,bn},n为地图顶点个数。根据式(5),bi可取值0、1、2,由差值di选取的参考坐标及是否与虚拟坐标重合两个条件确定。参考坐标标识图能为后续水印正确提取提供依据,为提高算法效率,对参考坐标标识图L采用游程压缩编码,压缩率受区间步长lt的影响。

(5)

1.3 差值直方图平移

在基于差值扩展嵌入水印时,差值越小,引入的数据失真越小。因此,需对差值直方图进行平移,进一步降低差值的大小,以减少水印嵌入引入的数据失真。差值直方图峰值所在点记为dmax,则直方图平移按式(6)进行。

d′i=di-dmax

(6)

1.4 水印的嵌入、提取和原始数据恢复

水印嵌入的对象为差值直方图平移后的差值,水印的提取为水印嵌入的逆过程。为提高算法可读性,水印的嵌入、提取以及数据恢复以x坐标为例说明,y坐标的相关方法和流程与x坐标相同。

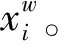
dw′i=d′i×2+w

(7)

(8)

(9)

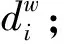
(10)

(11)

w=dw′i%2

(12)

3)数据恢复:①不含水印差值计算:依据式(13)计算不含水印的差值d′i;②差值直方图逆平移:按式(14)将所有差值d′i向右平移dmax恢复原始差值di;③原始坐标计算:结合参考坐标标识图L,按式(15)求得原始坐标。

d′i=floor(dw′i/2)

(13)

di=d′i+dmax

(14)

(15)

2 基于改进差值扩展的矢量地图水印方案

本文算法利用虚拟坐标和差值直方图对传统差值扩展技术进行改进(图2):在水印嵌入阶段,首先生成虚拟坐标,然后对基于虚拟坐标计算的差值直方图平移,差值扩展嵌入水印,形成含水印地图;水印提取阶段,在水印密钥的辅助下生成与嵌入阶段一致的虚拟坐标,获取含水印差值,提取水印验证数据来源;数据恢复基于差值扩展的逆过程,再经差值直方图平移变换求得原始差值,然后计算原始坐标,最终恢复原始地图。

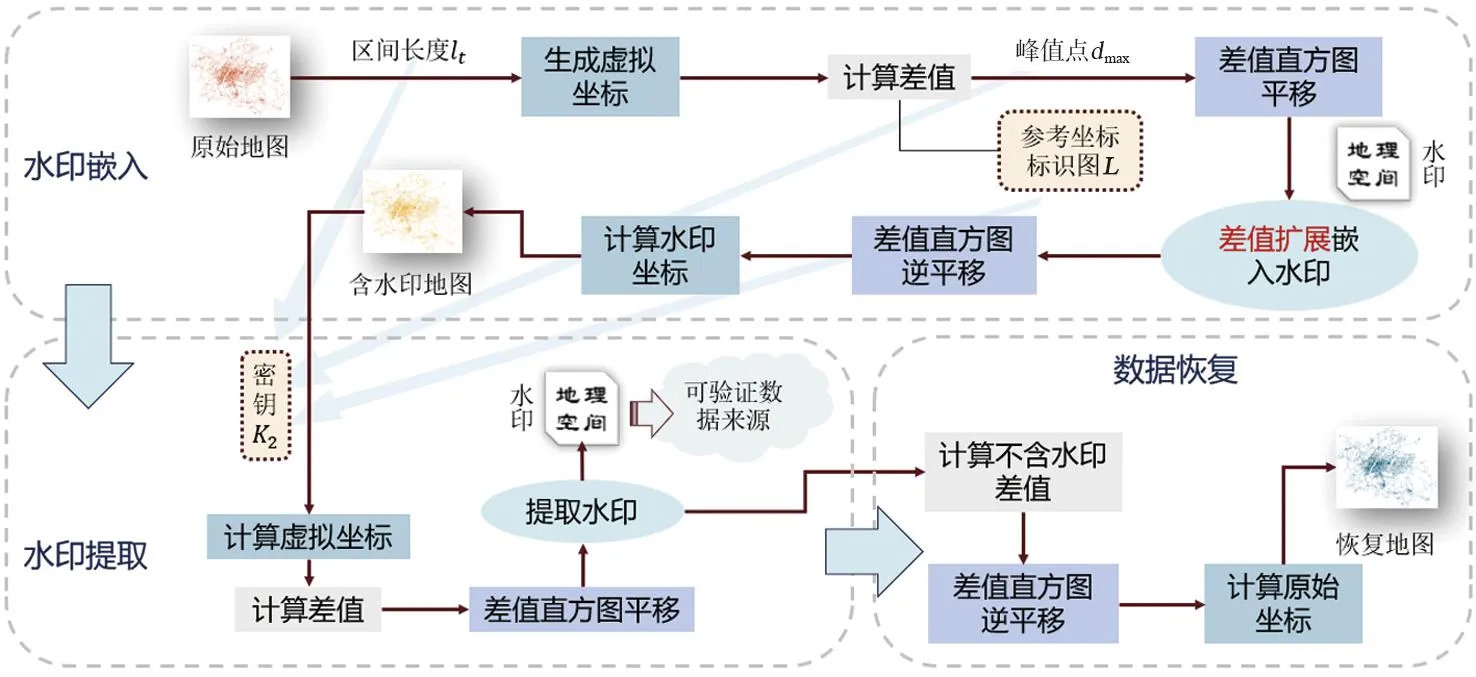
图2 本文算法框架

2.1 水印嵌入

(16)

式中:P为小数点向右移动的位数,Pmax=6。

将区间长度lt、参考坐标标识图L、差值直方图峰值点dmax、P值保存为密钥K2,用于后续水印提取与数据恢复。

2.2 水印提取和数据恢复

以x坐标为例,水印提取和数据恢复过程如下:

①遍历水印地图Mw所有顶点,按式(16)调节坐标,水印提取基于整数坐标;②读取密钥K2确定区间步长lt,参照1.1节生成虚拟坐标;③利用密钥K2中的参考坐标标识图L,按式(10)计算含水印差值;④按式(11)将含水印的差值直方图向左平移;⑤按式(12)提取水印,比较原始水印信息验证数据一致性;⑥基于式(13)求出不含水印的差值d′i;⑦按式(14)将差值直方图向右平移恢复原始差值di;⑧按式(15)得到整数化的原始坐标xi;⑨解除坐标整数化,获得原始地图M。

3 实验与分析

为验证算法的有效性,在Windows 10操作系统采用Visual Studio 2013开发平台进行实验。矢量地图数据由点、线、面要素构成,不同类型地图的数据相关性存在差异,本文选取具有代表性的风景名胜POI、等高线、路网和居民地矢量数据(图3)进行实验,数据格式为Shapefile,基本信息如表1所示。实验中原始水印图像为写有“地理空间”的二值图像,大小为125×125像素,水印嵌入强度默认为1,逻辑映射的初始值k0= 0.635 435。

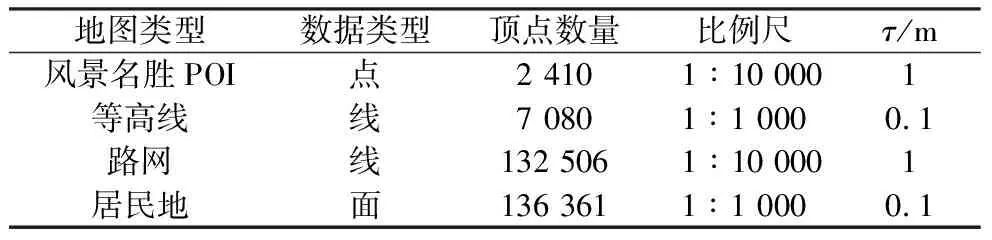
表1 原始矢量数据基本信息

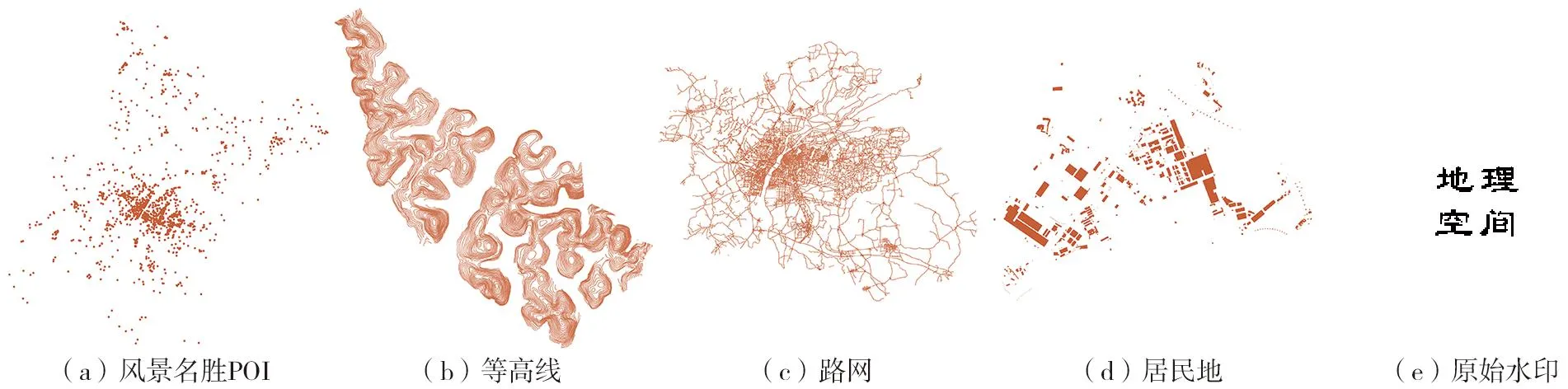
图3 原始实验数据

实验选取文献[11,17,23,24]中的算法作为本文对比算法。其中,文献[11]是传统矢量地图差值扩展可逆水印算法;文献[23]同为虚拟坐标在矢量地图水印的应用,但与本文构建虚拟坐标方法不同;文献[24]是针对文献[23]在2维 CAD工程图的改进算法;文献[17]为矢量瓦片数据鲁棒水印算法,该算法通过改进QIM方法嵌入水印,有效提升了水印容量但不可逆。

3.1 区间步长lt的讨论

本文算法中,确定区间步长lt是构建虚拟坐标的前提,不同P值下不同的区间步长所构建的虚拟坐标不同,用于水印嵌入的坐标差值也不同,区间步长lt越小,差值越小,基于差值扩展嵌入水印后的顶点扰动越小。因此,在相同水印嵌入强度下,区间步长越小越好。此外,为提升算法的水印容量,虚拟坐标与实际坐标的重合概率要尽可能小,因此要求区间步长尽可能大。综上,区间步长的选择本质上是数据精度与水印容量的平衡。

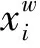
3.2 水印容量分析

水印容量即一个数据集可嵌入水印数量的上限,可用平均每个顶点所嵌入的水印比特数(bit/点)表示,即嵌入率。理论上每个顶点的水印容量为2 bit/点,本文算法中,水印嵌入在不与虚拟坐标重合的坐标中,如果部分实际顶点坐标与虚拟坐标重合,则重合坐标不嵌入水印,此时水印嵌入率小于2 bit/点。由图4可以看出,4个数据集的水印嵌入率均随lt增大而增大,最大达到2 bit/点,变化速度呈先快后慢趋势,除风景名胜POI数据外,在相同lt下,P值越大,水印容量越高;等高线数据集首次取得最大水印容量的lt大于其他3个数据集,这是由于坐标点分布越密集,在相同lt下,与虚拟坐标重合的实际坐标越多,水印嵌入率越低;风景名胜POI数据集由于顶点相关性较低,受P值变化影响小;当lt取最小值时,居民地数据集的水印容量最好。

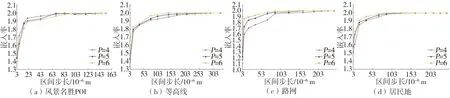
图4 水印嵌入率与区间步长lt的关系

由表2可以看出,当区间步长取合适值时,本文算法水印容量在不同数据集中稳定为2 bit/点,高出文献[11]的传统差值扩展方法6倍以上。文献[17]算法水印容量受嵌入位置影响,为便于比较,实验设定坐标可更改的精度位为6,量化区间数为2,即每个坐标嵌入一个水印位,水印容量与本文相同且点线面数据集均适用。理论上文献[24]算法迭代次数可趋近无限,故在不考虑其他水印性能的情况下,文献[24]算法的水印容量会远高于本文算法,但实验发现文献[24]算法应用于本文大比例尺地图时,迭代次数增加会不同程度地影响水印不可见性和计算复杂度,因此对比实验时迭代次数设为1。在同等水印嵌入强度下,文献[23]与文献[24]水印嵌入坐标数量相同,故水印容量相同。本文算法水印容量略高于文献[23,24],这是由于文献[23,24]算法不能将水印嵌入参考坐标中,而本文算法通过控制区间步长lt所有顶点均可参与水印嵌入。值得注意的是,虽然POI数据集的顶点相关性很低,但本文算法基于约束的区间步长lt引入虚拟坐标,以虚拟坐标为参考计算每个实际坐标的差值,水印可嵌入每个实际坐标中,故水印容量依然很好,而文献[11,24]在顶点分布稀疏的POI数据集中无法嵌入水印。综上,相对传统差值扩展方法,本文算法拥有更大的水印容量,且显著降低了顶点相关性对水印容量的影响。

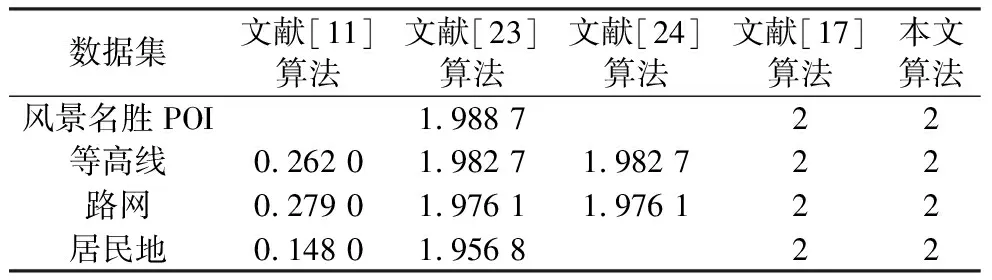
表2 不同算法水印容量比较(P=6)

3.3 水印不可见性分析

本文从主观和客观两方面评估水印数据的不可见性。①主观上,对嵌入水印后的数据与原始数据叠加比较,在ArcGIS中进行拓扑检查,未出现要素重叠等问题。观察图5发现,正常情况下水印嵌入前后地图无明显区别,局部放大发现坐标点出现微小偏移,但整体没有出现明显形变,要素拓扑关系保持良好。②客观上,依据式(17)和式(18)计算水印嵌入前后坐标点的均方根误差RMSE(ERMSE)和地图坐标最大改变量Max-R(RMax),二者数值越小,表示坐标偏移越小,水印不可见性越好。由图6和图7可知,4个数据集的RMSE和Max-R均随区间步长lt增大而增大;lt取相同值时,P值越大,同一数据集的RMSE和Max-R越小,等高线数据在4个数据集中的RMSE最小,不可见性最优;在相同P值下,4个数据集的Max-R变化曲线几乎相同,这是因为相同lt下坐标构建的最大差值相同。风景名胜POI数据集在P=5时的RMSE与P=6时相差较小,而其他3个数据集在P=5时的RMSE与P=4时更接近,P=6时不可见性显著提升。

(17)

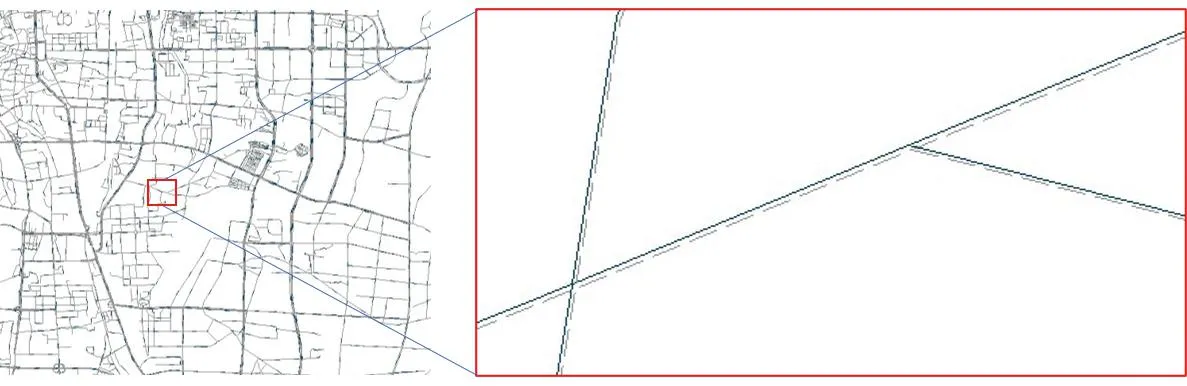
图5 水印嵌入前后细节对比(路网)

图6 Max-R与区间步长lt的关系

图7 RMSE与区间步长lt的关系

RMax=max(‖V-Vw‖)

(18)

从表3可以看出,本文算法应用于4种数据的地图坐标偏移很小,水印不可见性好。文献[17]作为不可逆水印算法,虽然拥有高水印容量,但水印坐标偏移量远高于本文算法和其他对比算法。与文献[11]相比,本文算法的RMSE和Max-R明显偏低,表明本文算法的坐标偏移量更小,图形质量更高,水印不可见性更好;与文献[23]比较,本文算法应用于风景名胜POI数据的RMSE和Max-R更小,但文献[23]应用于路网数据的不可见性与本文算法相差不大;文献[24]应用于等高线和路网数据的不可见性略差于文献[23],原因是文献[24]的水印坐标受虚拟坐标区间状态值影响;此外,本文算法在4种数据集中的RMSE相差不大,即使对顶点相关性低的POI数据集,也取得了与其他3个数据集相当的RMSE结果,这是因为虚拟坐标的构建提高了数据相关性,差值直方图平移减小了坐标扰动,整体上可嵌入水印的数据单元增加而数据失真保持在较小范围。

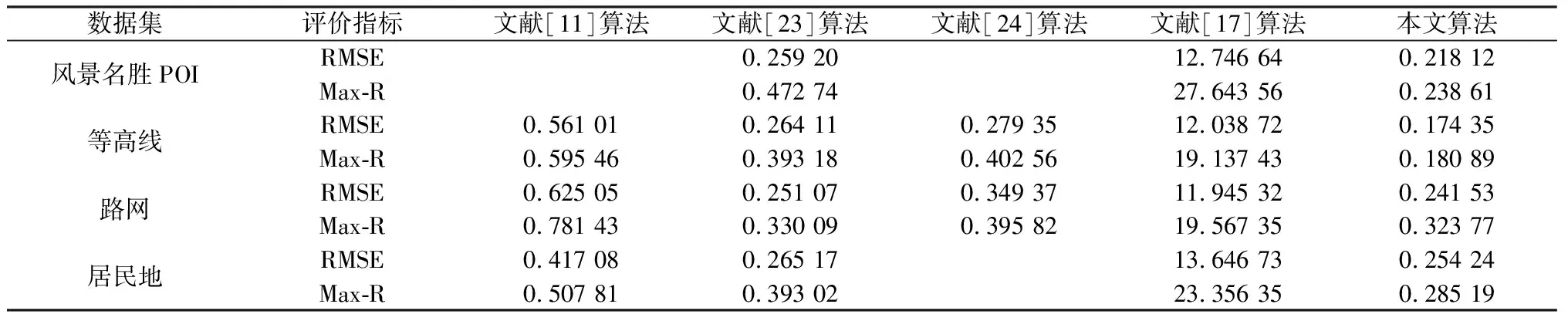
表3 不同算法水印不可见性比较(P=6)

本文算法实验中,1∶1 000的原始地图和水印地图之间的最大Max-R为 0.000 285 19<0.30 m(国标《1∶500 1∶1 000 1∶2 000外业数字测图技术规程 GB14912—2005》中的地形图精度平面误差要求),符合实际生产标准,其他4个测试数据的水印地图数据精度也均满足应用要求,因此,本文算法嵌入水印所引起的数据扰动不会影响矢量地图的可用性。

3.4 可逆性分析

为评价恢复地图客观质量,计算不同算法下原始矢量地图与恢复后矢量地图之间的RMSE和Max-R值(表4)。通常矢量地图数据存储精度约为0.1 mm,实验中原始坐标与恢复坐标之间的差异小于10-4m即认为方案可逆。理论上本文算法可以在正确提取水印的基础上无损地恢复原始地图,这是由本文算法机制决定的:本文算法和文献[11]算法是基于整数坐标进行运算,小数部分不参与水印嵌入,因此水印嵌入后的精度在运算过程中并无损失;另一方面,水印嵌入和数据恢复时差值直方图经过两次平移变换,两次变换互为逆运算,不会对地图坐标产生影响。文献[24]算法中,水印坐标含有失真参数Q,会影响水印提取恢复,文献[17]为鲁棒水印算法,无法从水印地图中恢复出可用的地图,因此算法不可逆。由表4可知,基于文献[23,24]算法的RMSE和Max-R虽然不为0,但数值极小,对地图数据质量的影响很小,因此也认为是可逆算法;从可逆性上看,文献[11]算法与本文算法最优。

4 结束语

本文基于传统差值扩展技术引入虚拟坐标计算差值,将构建的差值直方图平移,通过差值扩展将水印信息嵌入坐标,与传统差值扩展方法(文献[11])相比,有效提升了水印容量并减小数据扰动。与文献[23,24]的方法相比,本文算法虚拟坐标由区间步长lt构建,无需浪费参考坐标。同时,本文算法对于顶点相关性低的地图数据(如POI数据)同样适用,可以实现大比例尺地图的水印嵌入,在实际工程建设中具有现实意义。

本文未涉及高强度嵌入水印的情况,对于单个水印嵌入单元能否携带大量水印信息也欠考虑。因此,提升可逆水印算法的鲁棒性和探讨高水印嵌入强度的水印算法可行性是下一步的重点研究内容。