n 比特随机量子系统实时状态估计及其反馈控制

张骄阳 丛 爽 匡 森

自Huang 等[1]于20 世纪80 年代研究双线性量子系统能控性问题以来,量子控制这一交叉学科取得了快速发展,并受到了空前的关注,越来越多的专家学者开始从系统控制的角度审视量子系统控制,如早期广泛研究的量子门的制备与操作、退相干抑制等都可以归结为典型的开环控制问题[2-6].自21 世纪以来,宏观系统控制理论更深入地渗透到量子系统的操纵之中,两个突出特点是[7-12]: 1) 从建模的角度上,研究的模型从简单的低维双线性封闭量子系统,逐渐转变为更符合实际物理系统的开放量子系统,如马尔科夫(Markovian)开放量子系统、非马尔科夫(Non-Markovian)开放量子系统以及随机量子系统;2) 从控制任务的角度上,研究的问题从分析量子系统的能控性、能观性和可逆性以及针对某一特定的控制目标设计开环控制律,逐渐深化为借助宏观控制理论设计具有普适性的反馈控制律,以实现量子系统状态的转移、保持或跟踪等复杂的控制目标.与Markovian 和Non-Markovian 开放量子系统不同的是,随机量子系统在建模时还考虑了由连续弱测量(Continuous weak measurement,CWM) 引起的不可忽略的反向效应(Back-action),这给实时量子状态估计带来了挑战.作为未来量子科技中不可或缺的基础理论与关键技术,随机量子系统的实时状态估计和高精度反馈控制逐渐成为了量子系统控制领域新的热点问题.

量子状态估计(Quantum state estimation,QSE)在量子物理领域又称为量子状态层析(Quantum state tomography,QST),分为测量和状态重构两个主要步骤.传统意义上的n比特量子系统的状态层析指的是对d×d(d=2n) 密度矩阵ρ的大量全同副本进行至少d2-1 次投影测量和多次算法迭代计算出满足单位迹和半正定量子状态约束的厄米(Hermitian) 矩阵基于大量全同副本的量子状态估计只能离线完成,然而高精度量子反馈控制则要求实时估计随时间变化的量子状态,这是实现基于测量的量子反馈控制必须解决的一个难点问题.Silberfarb 等[13-14]和Ralph 等[15]提出的CWM为实时量子状态估计的物理实现提供了可能.2020 年,唐雅茹等[16]和Harraz 等[17]以CWM 为基础,基于MATLAB CVX 工具箱中的最小二乘法针对单比特随机量子系统提出了一种密度矩阵实时重构的方案,并研究了噪声幅值等系统参数对于实时量子状态估计算法性能的影响.Zhang 等[18]通过在凸优化问题中引入布雷格曼(Bregman)散度使得不存在解析解的密度矩阵恢复子问题可以被求解,并提出了一种基于在线交替方向乘子法(Online alternating direction multiplier method,OADM) 的实时量子状态层析算法QST-OADM.此外,Zhang 等[19]将实时量子状态估计描述为一个稀疏促进半定规划问题,并结合在线邻近梯度法(Online proximal gradient,OPG)和交替方向乘子法(Alternating direction method of multipliers,ADMM)设计出OPG-ADMM 算法求解该问题.

在量子系统控制领域,李雅普诺夫控制方法是一种常用的控制律设计方法,该方法的一大优势是能够得到解析形式的控制律.Kuang 等[20]于2008年总结了非退化的封闭量子系统三种本征态制备方法.Sayrin等[21]于2011 年实现了超导腔中微波场中Fock 态的全局镇定,进而逆转了退相干引发的量子跃迁效应.Qi 等[22-23]全面地比较了多种形式的量子主方程本征态反馈镇定控制方案的性能,并指出CWM 过程造成的量子状态随机塌缩不仅在一定意义上有利于反馈控制的实现,还能够完成开环控制理论上无法实现的控制任务.2019 年,Qamar等[24]针对具有马尔科夫退相干的二能级随机量子系统提出了一种基于非线性最优观测器的本征态反馈控制方案,但该方案难以推广到高维量子系统中.同年,Harraz 等[25]在其提出的实时量子状态估计方案的基础上,针对一类特殊的n比特随机量子系统设计出一种连续形式的本征态反馈控制律,不过没有严格地给出关于控制律收敛性的数学证明.目前,状态的实时获取仍然是基于李雅普诺夫控制方法的随机量子系统反馈控制中的瓶颈问题.对于一个d维的随机量子系统,在线求解其随机主方程就相当于在线求解d2-1 个随机微分方程,如此庞大的计算量易导致反馈环路中存在延迟从而导致较差的控制效果.如能通过快速高效的算法进行实时量子状态估计,则高性能的量子反馈控制就有可能实现.

本文针对CWM 过程中存在高斯噪声的n比特随机量子系统,提出一种基于OADM 的实时量子状态估计算法 (简称QSE-OADM 算法),然后基于QSE-OADM 算法设计了一种反馈控制 (Feedback control,FC)方案 (简称QSE-OADM-FC 方案),实现了基于实时状态估计的量子反馈控制.本文的贡献在于: 1) 在实时量子状态估计算法的推导过程中,将时变的密度矩阵实时重构问题和最小化高斯测量噪声问题分开求解,进行状态在线更新时无需求解一阶随机梯度信息,得到比文献[18]中的QST-OADM 算法和文献[19]中的OPG-ADMM 算法更快的收敛速度和更短的耗时;2) 借鉴文献[26]的思想,针对n比特随机量子系统,运用李雅普诺夫控制方法设计出一种新颖的反馈控制律,并对控制律的渐近收敛性进行了严格的数学证明;3) 在2比特随机量子系统本征态和叠加态的反馈控制数值实验中,通过与基于QST-OADM 算法和OPGADMM 算法的量子反馈控制方案进行性能对比,展现所提量子反馈方案的优越性.

本文的结构安排如下: 第1 节为在CWM 作用下,本文所提出的测量值序列和采样矩阵的构造方法;第2 节为用于实时量子状态估计的QSE-OADM算法的推导及其性能分析;第3 节为基于实时状态估计的n比特随机量子系统反馈控制律的设计及其性能对比分析;第4 节为结束语.

1 CWM 作用下测量值序列和采样矩阵的构造

在薛定谔(Schrödinger)绘景下,一类典型的n比特随机量子系统的主方程可以表示为[16-18,23]

其中,ℏ 为约化普朗克常量(为方便,取 ℏ=1);ρt为t时刻的密度矩阵;H(t) 为系统哈密顿量;L为测量算符,上标“†”代表共轭转置;η∈(0,1] 为测量效率;dW为标准实值维纳过程并满足E[dW]=0 和 E [(dW)2]=Δt;D(L,ρt)Δt刻画了测量过程带来的确定性的退相干作用,而H(L,ρt)dW则刻画了测量过程引起的随机的量子状态塌缩.

根据CWM 过程及其推导,可以得到作用在单比特随机量子系统状态上的 2×2 的测量算符为[16]

其中,I为 2×2 的单位矩阵,H′(t)=H0+Hc(t)=H0+u1(t)H1,L′=ξσ,ξ为被测量子系统与探测系统之间的相互作用强度,σ可在Pauli 矩阵σx=[01;10],σ y=[0-i;i0] 和σz=[10;0-1]中选择.综合考虑测量效率及其反向效应的影响,可得 2×2 密度矩阵的演化算符为[16-18,23]

更一般地,对于n比特随机量子系统,其2n×2n的测量算符、密度矩阵演化算符可以在单比特量子系统的基础上借助Kronecker 积“⊗”构造为

令t=k·Δt,k=1,2,···,N,可以得到与式(1) 等价的离散型n比特随机量子系统的密度矩阵和测量算符的演化方程为

本文将k时刻及其之前的测量值共同组成一个测量值序列b k=[y1,···,yi,···,yk]T.测量值序列的具体构造方法如表1 所示.

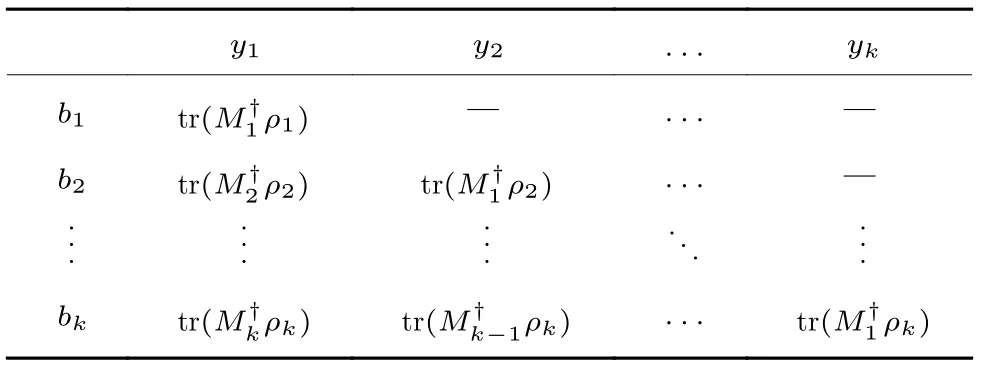
表1 测量值序列的构造方法Table 1 Construction approach of the measurement record sequence

容易看出,随着k取值的增大会加重实时量子状态估计算法的计算负担,进而导致较长的迭代时间.因此,本文借鉴递推限定记忆最小二乘法的思想引入滑窗以便保证在充分利用测量值的历史信息的同时,不至于使得计算负担过重.滑窗中的数据按照“先入先出”的策略进行更新,即数据量达到滑窗长度l之后,每增加一个新数据信息的同时,删除一个老数据的信息,数据的长度维持不变.带有滑窗的测量值序列为

与文献[13-15]中在海森堡(Heisenberg)绘景下借助量子系统动态演化的模型获取k时刻量子状态的方法不同,本文提出的测量值序列构造方法能够实时估计出k时刻的量子状态.

根据测量值与密度矩阵之间的关系式(6),可以得到与bk对应的采样矩阵Ak为

当采样次数大于等于l时,Ak保持不变.考虑到CWM 过程额外引入的高斯噪声,式(6)应修正为

其中,e i∈R为高斯白噪声.此时,n比特随机量子系统在CWM 作用下,bk与Ak的关系为

2 QSE-OADM 算法的推导及其性能分析

本节将推导一种基于OADM 的n比特随机量子系统状态实时估计的算法QSE-OADM,并以2比特量子系统为例进行数值仿真实验,研究相互作用强度ξ、测量算符的初始值M1及其与系统哈密顿量H′形成的夹角对所提算法性能的影响.

2.1 QSE-OADM 算法的推导

本文采用OADM 算法进行实时量子状态估计.对于式(10)所示的可分离的双目标在线约束凸优化问题,OADM 算法的基本思想是将其分解为两个子问题并交替求解,其框架是依次最小化两个原始变量对应的增广拉格朗日(Lagrangian)函数,最后通过对偶梯度上升来更新拉格朗日乘子.此外,在每个采样时刻k过后,该算法只需进行一次更新即可计算原始变量和拉格朗日乘子.式(10)对应的增广拉格朗日函数为

其中,λ为拉格朗日乘子,α＞0 是惩罚参数.

2.1.1 求解相关子问题

根据矩阵求逆引理[28],得到

因此,式(14)可以重写为

式(21)对应的拉格朗日函数为

2.1.2 求解相关子问题

所提出的QSE-OADM 算法的具体步骤如算法1 所示.

算法1.QSE-OADM 算法

下面讨论QSE-OADM 算法的计算复杂度.对于QSE-OADM算法而言,其密度矩阵依据式(17)更新时,的计算复杂度为由于采样矩阵Ak在采样次数达到l之后保持不变,因此这一部分总的计算复杂度为l×O(l2d2).另外,奇异值分解的计算复杂度为 O (d3),由于计算过程中待估计的密度矩阵始终严格满足量子状态约束,因此采样次数为N时这一部分总的计算复杂度为N×O(d3).综上可知,QSE-OADM 算法总的计算复杂度为l×O(l2d2)+N×O(d3).

2.2 QSE-OADM 算法的性能分析

采用保真度 (Fidelity) 来衡量量子状态估计的精度,其定义为

2.2.1 不同外部控制场的作用对实时量子状态估计性能的影响

外部控制量和控制哈密顿量的乘积u1H1分别选取为0,σx,σy和 10σx,固定H0=σz,M1=σz⊗σz,L′=0.7σz.不同方向的外部控制场对QSEOADM 算法实时状态估计的实验结果如图1 所示,从中可以看出: 当初始测量算符M1与H0平行时,QSE-OADM 算法无法有效获取到随机量子系统状态演化的信息,此时该算法失效.解决该问题的一种可行的方案是通过施加外部控制场来使M1与系统哈密顿量H′=H0+u1H1之间存在一定的夹角.

图1 不同外部控制场的作用下的实时状态估计性能Fig.1 Real-time state estimation performance under various external control fields

需要注意的是,外部控制场并非越强越好,过大的控制量(如图1 中带圆圈的曲线所示的情况)可能导致M1与H′之间的夹角接近 90°而呈现出二者近似正交的情况,此时CWM 同样难以获取到系统演化的信息而导致QSE-OADM 算法估计精度下降.

2.2.2 不同初始测量算符 M1 对实时量子状态估计性能的影响

初始测量算符M1分别选取为σ x ⊗σx、σy ⊗σy和σ z ⊗σz三种情况,固定H′=H0+1·σx,L′=0.7σz.不同初始测量算符对QSE-OADM 算法估计状态的实验结果如图2 所示.从图2 中可以看出只要M1与系统哈密顿量H′不平行且不正交,三种情况均能实现有效的实时量子状态估计,不过每一种情况下QSE-OADM 算法的收敛速率不同.实验结果表明: 当M1=σz ⊗σz时QSE-OADM 算法的实时状态估计性能最好.

图2 不同初始测量算符作用下的实时状态估计性能Fig.2 Real-time state estimation performance under various initial measurement operators

2.2.3 不同相互作用强度 ξ 对实时量子状态估计性能的影响

相互作用强度ξ分别取0.3,0.5,0.7,0.9,固定H′=H0+1·σx,M1=σz ⊗σz,测量算符选取σz.被测量子系统与探测系统之间不同的相互作用强度对于QSE-OADM 算法性能影响的实验结果如图3所示,从中可以看出:ξ与保真度成正相关,即ξ越大QSE-OADM 算法的收敛性越好.

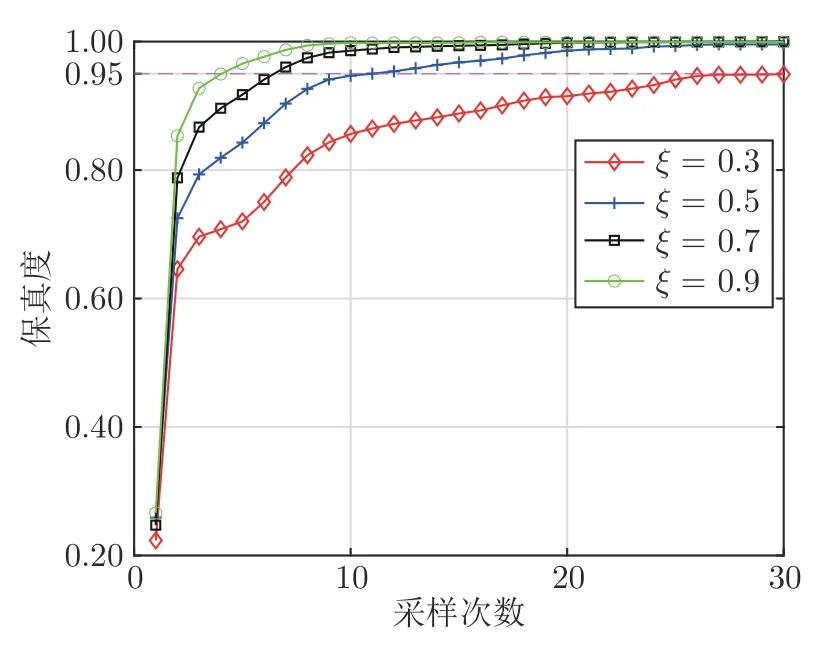
图3 不同的相互作用强度作用下的实时状态估计性能Fig.3 Real-time state estimation performance under various interaction strengths

当ξ ≥0.7 时,QSE-OADM 算法已经具有良好的实时量子状态估计性能,第7 次采样过后保真度高于95%,第30 次采样时保真度高于99.95%.第30 次采样时的估计状态和真实状态如图4 所示,其中,x轴和y轴分别代表密度矩阵的行和列,z轴代表密度矩阵元素的实部数值.

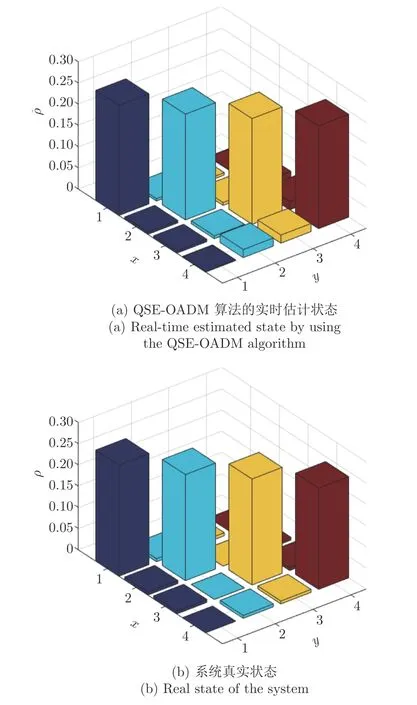
图4 第30 次采样时2 比特量子系统估计状态与真实状态比较 (H′=H0+1·σx,M1=σz ⊗σz,L′=0.7σz)Fig.4 Comparison between the estimated state and the real state of a 2-qubit system at the 30th sampling time(H′=H0+1·σx,M1=σz ⊗σz,L′=0.7σz)

3 基于实时状态估计的量子反馈控制律的设计及其性能对比分析

本节将采用基于李雅普诺夫稳定性定理的控制方法设计反馈控制律,结合所提出的实时量子状态估计算法实现n比特随机量子系统的反馈控制,并以2 比特随机量子系统为例针对目标态为本征态和叠加态的情况分别进行数值仿真实验及其性能对比分析.

3.1 反馈控制律的设计及其收敛性的证明

第2 节基于QSE-OADM 算法实现了n比特随机量子系统的实时状态估计,因此可将式(1)改写为包含估计状态的随机主方程,即

其中,系统哈密顿量为H(t)=H0+Hc(t),内部哈密顿量为H0,相互作用哈密顿量为Hc(t)=其中控制哈密顿量的个数r≥2,ui(t)表示控制场的第i个分量.

基于实时状态估计的n比特随机量子系统反馈控制系统的框图如图5 所示,其中,S,P,S ⊗P分别代表被测量子系统、探测系统和联合系统,|ψ(Δt)〉代表联合系统的状态矢量,|o〉 代表系统P在投影测量后随机塌缩到的某个本征态,M代表测量算符,它们一起组成CWM 过程.联合系统y的输出中包含测量过程引入的高斯噪声,分别为在k时刻的密度矩阵ρ k和测量噪声ek的估计值,u(k)为k时刻的控制场,q-1为单位延迟算子,ρf为目标态.

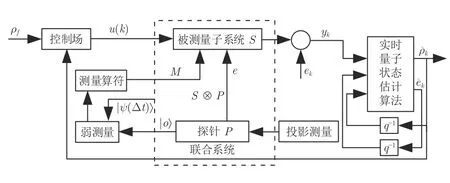
图5 基于实时状态估计的n 比特随机量子系统反馈控制方案的框图Fig.5 Real-time state estimation-based feedback control scheme for n-qubit stochastic quantum systems

定理 1.对于n比特随机量子系统(28),当满足能控性条件L=L†和[H0,L]=0[29]时,在式(29)和式(30)所示的反馈控制律的作用下,量子系统的状态可以从任意初态ρ0以概率1 收敛到任意期望的目标态ρf.控制律的表达式为

1) 当采样时刻k=1 时

2)当采样时刻k ≥2 时

1) 系统(28)存在多个平衡点,如ρs1=diag{1,0}⊗n和ρ s2=diag{0,1}⊗n.当初始估计状态与目标态ρf选取为同一个平衡点时,有意味着式(30) 所示的控制律无法施加到该量子系统中.因此在k=1 时,首先施加微扰形式的控制律驱动系统离开平衡点;即便是系统初始状态不是平衡点,该微扰形式的控制律也不会对系统动力学产生较大的影响.

将式(33)和式(35) 代入式(31),可得

将式(30)所示控制律代入式(36),可得

基于QSE-OADM 算法进行实时量子状态估计的反馈控制方案QSE-OADM-FC 的具体步骤如算法2 所示.

算法2.QSE-OADM-FC 方案

3.2 量子反馈控制的数值仿真实验及其性能对比分析

本节仍以2 比特随机量子系统为例进行数值仿真实验.仿真实验中,H0=σz ⊗I+I ⊗σz,4 个控制哈密顿量分别为H1=σx ⊗I+I ⊗σx;H2=σy ⊗I+I ⊗σy;H3=(σy+σz)⊗I+I ⊗(σy+σz);H4=(σx+σz)⊗I+I ⊗(σx+σz).除滑窗长度改为l=30 外,其他系统参数以及QSE-OADM 算法的参数均与第2 节相同.

为了验证本文所提方案性能的优越性,将所提出的QSE-OADM-FC 方案与QST-OADM-FC 方案以及OPG-ADMM-FC 方案进行比较,其中QSTOADM 算法和OPG-ADMM 算法的参数已分别依据文献[18]和文献[19]调整至最佳.除李雅普诺夫函数数值之外,本文还借助控制场能量这一指标来衡量反馈控制方案的优越性,其定义为

3.2.1 本征态的反馈控制

2 比特量子系统的初态为本征态ρ0=ρ00⊗ρ00,其中ρ00=[1 0;0 0];目标态为本征态ρ f=ρf0⊗ρf0,其中ρ f0=[0 0;0 1],设计参数为g2=6,g3=1,g4=1.本征态反馈控制的仿真结果如图6 所示,其中,图6(a)和图6(b)中的实线、虚线和点线分别代表QSE-OADM-FC、QST-OADM-FC 和OPGADMM-FC 方案中保真度和李雅普诺夫函数的变化曲线,图6(c)中的实线、虚线、点划线和带“+”的曲线分别代表3 种方案中控制场分量u1,u2,u3和u4的变化曲线,图6(d)中的实线、虚线、点划线和带“+”的曲线分别代表3 种方案中密度矩阵对角线元素ρ11,ρ22,ρ33和ρ44的变化曲线.

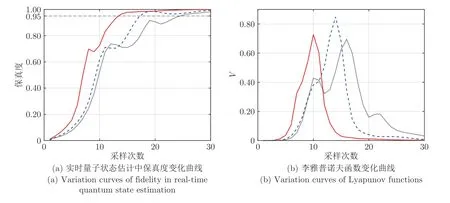
图6 本征态反馈控制的仿真结果Fig.6 Simulation results on feedback control of an eigenstate

在QSE-OADM-FC 方案中,第14 次采样过后即可保证实时量子状态估计的保真度高于95%;第15 次采样过后即可保证李雅普诺夫函数数值小于0.01;第30 次采样时保真度为99.84%,李雅普诺夫函数数值为 5.399×10-4.如采用QST-OADM-FC方案,则第18 次采样过后才能保证实时量子状态估计的保真度高于95%,李雅普诺夫函数数值小于0.01;第30 次采样时保真度为99.40%,李雅普诺夫函数数值为 1.484×10-3.如采用OPG-ADMM-FC方案,则第25 次采样过后才能保证实时量子状态估计的保真度高于95%;第28 次采样过后才能保证李雅普诺夫函数数值小于0.01;第30 次采样时保真度为98.29%,李雅普诺夫函数数值为 6.312×10-3.此外,采用QSE-OADM-FC 方案在达到更好的本征态反馈控制效果的同时所需要的控制场能量更小,仅为QST-OADM-FC 方案的60%左右,为OPGADMM-FC 方案的35%左右.

3 种方案下,本征态反馈控制性能指标的对比如表2 所示.其中,方案1 代表QSE-OADM-FC 方案;方案2 代表QST-OADM-FC 方案;方案3 代表OPG-ADMM-FC 方案.k s1代表使得保真度持续稳定在95%以上的首个采样时刻;k s2代表使得李雅普诺夫函数数值持续低于0.01 的首个采样时刻.

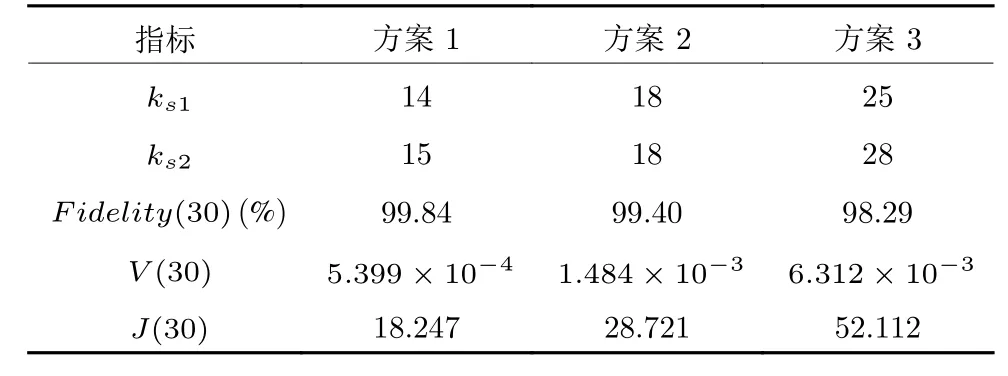
表2 本征态反馈控制性能指标的对比Table 2 Comparison of performance indicators of feedback control of an eigenstate

3.2.2 叠加态的反馈控制

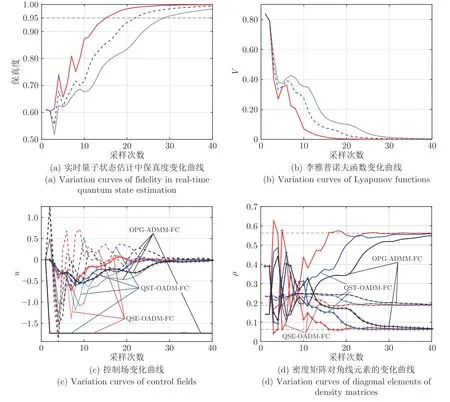
图7 叠加态反馈控制的仿真结果Fig.7 Simulation results on feedback control of a superposition state

3 种方案下,叠加态反馈控制性能指标的对比如表3 所示,其中k s1和k s2的含义与表2 相同.与本征态的反馈控制相比,叠加态的反馈控制实现起来难度更大,具体表现在其调节时间更长且所需的控制场能量更大上.

表3 叠加态反馈控制性能指标的对比Table 3 Comparison of performance indicators of feedback control of a superposition state

4 结束语

本文解决了n比特随机量子系统的实时状态估计及其反馈控制的问题.针对 CWM 过程中存在高斯噪声的n比特随机量子系统,通过测量序列和采样矩阵的构造、基于在线交替方向乘子法的实时量子状态估计算法的设计以及借助李雅普诺夫方法的反馈控制律的设计,提出了一种基于实时状态估计的量子反馈控制方案.最后,与基于其他两种不同的实时状态估计算法的量子反馈控制方案进行性能对比,展现了本文所提方案的优越性.