一种管道强制电流阴极保护长度和电流的计算方法

刘 国

(北京凯斯托普科技有限公司, 北京 100000)

确定阴极保护的有效范围以及阴极保护电流需求是管道阴极保护设计的重要环节。单个阴极保护站的保护距离是有限的,这是因为管道防腐蚀层有诸多破损或缺陷,且沿线存在接地、外部搭接等因素,导致距离阴极保护站较远的管段无法得到足够的保护电流。这种保护效果逐渐减弱的现象是一种衰减效应。

《阴极保护手册》是较早的基于衰减公式推导得到管道阴极保护距离公式的书籍[1]。其后国内一些书籍、标准[2-3]中提出的管道阴极保护距离计算方法与《阴极保护手册》中的方法是一致的。其中管道保护长度的计算公式见式(1):

(1)

(2)

式中:LP为单侧保护管道长度(m);ΔV为极限保护电位与保护电位之差(V);DP为管道外径(m);JS为保护电流密度(A/m2);RS为管道线电阻(Ω/m);ρ为钢管电阻率(Ω·mm2/m);δ为管道壁厚(mm)。

保护电流的计算公式见式(3):

2I0=2π×DP×JP×LP

(3)

式中:I0为单侧管道保护电流(A);DP为管道外径(m);JP为保护电流密度(A/m2);LP为单侧保护长度(m)。

上述公式在管道阴极保护领域有着广泛应用。但长期以来,业界对公式中存在的问题及准确性没有深入研究。为提升管道阴极保护距离计算的准确性,对计算公式中的一些有误释义进行修正,笔者基于传输线原理对管道阴极保护范围和保护电流的计算过程进行了推导,根据推导结果提出了基于衰减效应的准确的保护距离计算公式,并对以往计算公式的误差进行了分析。

1 电位偏移与保护电流密度

埋地钢质管道的防腐(蚀)层电阻率rC(Ω·m2)是评价防腐层绝缘性能的重要指标,也是管道阴极保护设计的重要参数。GB/T 21246-2007《埋地钢质管道阴极保护参数测量方法》对防腐层电阻率的定义为防腐层电阻和防腐层表面积的乘积。

电位偏移指管道阴极保护通电的瞬间,管道与远地之间的路径上产生的电压降,它不考虑极化。阴极保护汇流点处的电位偏移是最大的,保护的末端,电位偏移是最小的。电位偏移不是阴极保护评价准则,但电位偏移与阴极保护电流密度是相关的,因此可以利用电位偏移来估算实现有效保护所需的电流。

管道业界早期大量实践经验表明,对埋地管道施加阴极保护电流后,如果管道对地电位偏移能达到300 mV,就足以实现有效的阴极保护。时至今日,利用电位偏移和防腐层电阻率计算阴极保护电流密度的方法仍然广泛应用。若令管道的电位偏移达到300 mV,在防腐层电阻率已知的情况下,阴极保护电流密度(JCP)的取值为:

(4)

2 衰减原理

传输线理论是非常成熟的电学理论,用于计算传输线上传输波的电压及电流变化。在理论计算中可将传输线作为分布参数来处理,得到传输线的等效电路,然后由等效电路根据基尔霍夫定律导出传输线方程,求解传输线方程得到电压和电流随时间和空间的变化规律。

如果传输线上的分布参数是均匀的,可以将均匀传输线分割成许多微元段dz,每个微元段可看作集中参数电路,用一个Γ型网络来等效。整个传输线的等效电路是无限多个Γ型网络的级联,如图1所示。

图1 传输线理论模型(左:单个微元段;右:无限多个Γ型网络的级联)Fig.1 Theoretical model of transmission lines (left: single element segment; right: cascaded infinite multiple type networks)

阴极保护中涉及的衰减问题的研究方法起源于传输线理论。对埋地钢质管道沿线的电位和电流衰减起决定性作用的是管道的纵向电阻和防腐层的对地泄漏电阻。在以下推导中使用rS(Ω/m)代表单位长度管道的纵向电阻,使用rL(Ω/m)代表单位长度管道的对地泄漏电阻。

管道对地泄漏电阻用于表征管道与大地之间的电阻。管道外带有防腐层,它起到对地绝缘的作用。然而,完美的防腐层是不存在的,阴极保护电流将通过管道防腐层缺陷进入管道。管道对地泄漏电阻的数值主要取决于管道防腐层的状况和土壤电阻率。单位长度管道对地泄漏电阻rL的计算方法见式(5)。

(5)

式中:rC为管道防腐层电阻率(Ω·m2);D为管道外径(m)。

假定某管道长为L,管道防腐层绝缘性能均匀一致,管道沿线土壤电阻率也是一致的。在管道左端安装强制电流阴极保护设备,汇流点见图2。在距离汇流点x处的管道上取一微元段dx。在施加阴极保护电流的瞬间,dx段管地电位发生负向偏移,偏移为E。

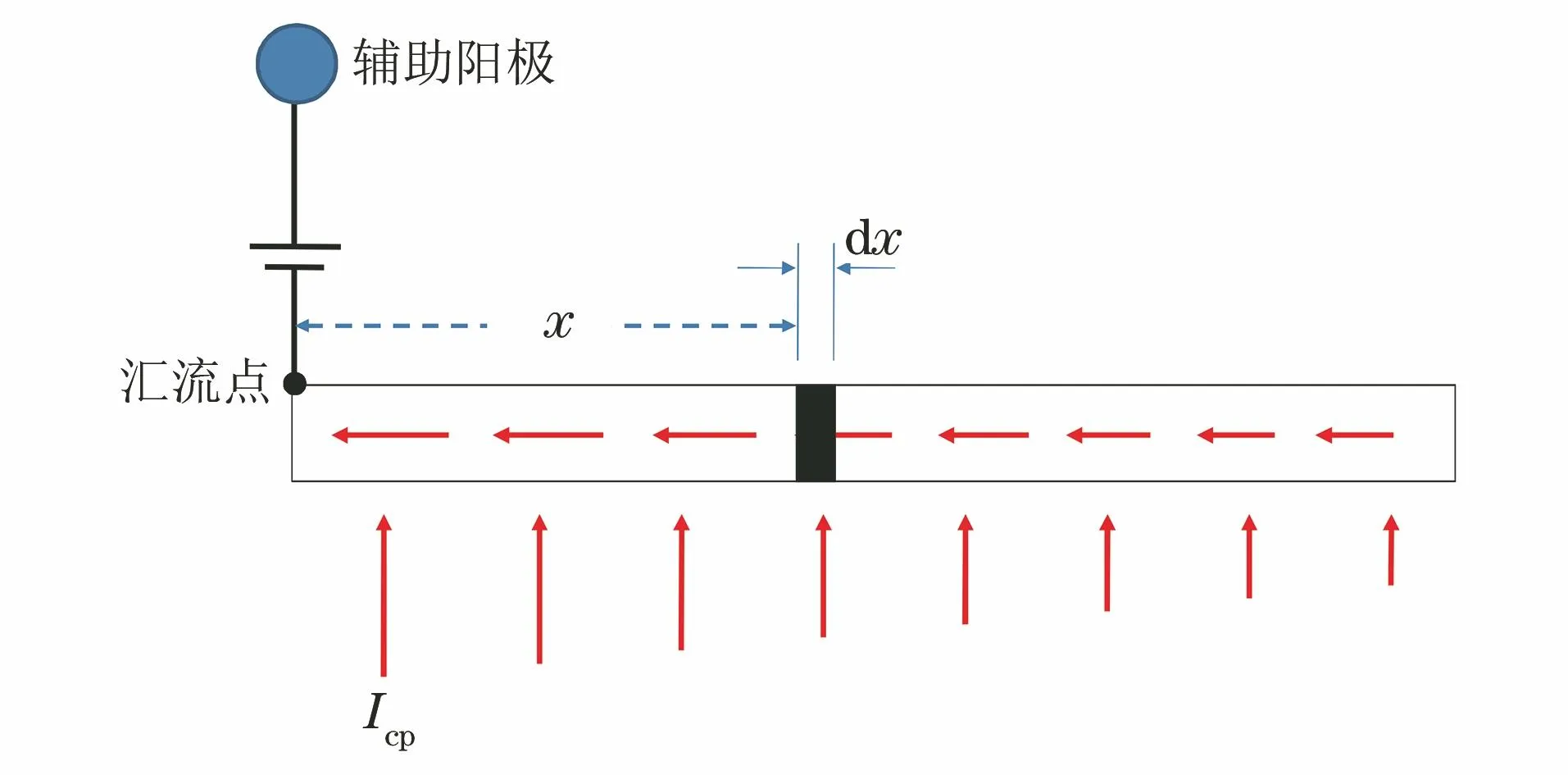
图2 有阴极保护管道上微元段示意Fig.2 Schematic of micro element segments onpipelines with cathodic protection

由于阴极保护设施安装在管道的左端部,因此管中电流自右向左汇入汇流点。dx段的电流增量dI就是从外部电解质进入该微元段的保护电流,存在以下的关系:

(6)

式(6)中负号表示电流的流动方向与x的增量方向相反。

此外,管中电流I沿管道流动时,由微元本身的电阻所产生的压降在数值上等于dE,存在以下关系:

(7)

(8)

(9)

式(8)和(9)为二阶常系数线性微分方程,它的解可以分为两种情况。第一种情况是无限长管段,即全线只有一个阴极保护站,线路上没有绝缘装置;第二种情况是有限长管段,即管道长度有限或在保护段终点有绝缘装置。

对于管道长度无限的情况,上述微分方程的解为:

E=ES×e-αx

(10)

I=IS×e-αx

(11)

式中:E为距汇流点x处位置管道对地的电位偏移(V);I为距汇流点x处位置的管中电流(A);ES为汇流点处管道对地的电位偏移(V);IS为汇流点处的管中电流,即阴极保护电流(A)。

对于管道长度有限或者末端施加了绝缘装置的情况(见图3),令管道长度为L,上述微分方程的解为:

图3 管道沿线电压和电流计算方法示意Fig.3 Schematic diagram of voltage and current calculationmethods along pipelines

E=ELcosh(ay)+RGILsinh(ay)

(12)

I=ILcosh(ay)+(EL/RG) sinh(ay)

(13)

E=EScosh(ax)-RGISsinh(ax)

(14)

I=IScosh(ax)-(ES/RG)sinh(ax)

(15)

式(12)和式(13)使用管道阴极保护末端的电位偏移和管中电流计算了考察位置的E和I;式(14)和(15)使用管道阴极保护始端的电位偏移和管中电流计算了考察位置的E和I。

上述公式推导过程中用到的α也称为管道的衰减系数,它取决于管道的纵向电阻和对地泄漏电阻。管道纵向电阻越小、管道对地泄漏电阻越大,则衰减系数越小,阴极保护电流沿管道的分布越均匀。

3 阴极保护范围与保护电流

在目前的管道阴极保护设计案例中,管道的长度都有限或者安装了绝缘装置,故仅根据管道长度有限时的衰减公式讨论阴极保护的范围。

以图3所示管道为例,阴极保护的汇流点安装在管道左侧端部,管道长度为L,汇流点处的电位偏移为ES,阴极保护末端的电位偏移为EL,末端管中电流IL为0。则根据式(12)可以得到:

ES=ELcosh(aL)

(16)

进而得到:

(17)

一般来说,阴极保护末端的电流密度取值应令此处的电位偏移达到300 mV。而在阴极保护的汇流点处,为了避免过度保护,电位偏移要控制在600 mV左右(有时也取650 mV)。即ES/EL=2,可以进一步简化式(17)得到单侧保护距离L:

(18)

也可以用级数展开的方式对L进行简化求解。先定义管道两端的电位偏移差为ΔE,根据式(12)可以得到:

ΔE=EL×[cosh(αL)-1]

(19)

cosh(αL)的级数展开公式为:

(20)

忽略掉级数展开中的高阶分量后,式(19)可以简化为:

(21)

计算得到单侧保护长度L为:

(22)

式中:JCP为阴极保护末端的保护电流密度,A/m2。

该公式与相关阴极保护标准[3]中提出的计算公式[见式(1)]的形式是一致的。但该公式中ΔE为管道两端的电位偏移差,若阴极保护末端的电位偏移取300 mV,汇流点处的电位偏移取600 mV,则ΔE为300 mV。

式(22)中的阴极保护电流密度JCP是阴极保护末端的电流密度,由于管道沿线电流密度不一致,存在衰减情况,所以不能用JCP来计算管道总的阴极保护电流。对于图3中长度为L的管道,根据式(15),其所需保护电流为:

(23)

此处ES取600 mV。

整条管道的平均电流密度JCP,avg为:

(24)

公式(18)和(22)都可以计算管道阴极保护距离。在公式(22)中对cosh(αL)的级数展开进行了高阶分量的省略,它的保护距离计算结果大于公式(18)。

在公式(3)中,如果保护电流密度取阴极保护末端管道的保护电流密度,计算得到的总保护电流值是偏非保守的。事实上在防腐层电阻率均匀一致且土壤电阻率均匀的情况下,末端的保护电流密度是最低的,阴极保护始端的保护电流密度是最高的。应使用式(23)计算管道所需阴极保护电流。

假定管道外径1 016 mm,壁厚18 mm,钢的电阻率0.166 Ω·mm2/m,防腐层电阻率为105Ω·m2。计算得到衰减系数为9.689 46×10-6。假定当管道对远地的电位偏移达到300 mV时能实现有效阴极保护,汇流点处电位偏移取600 mV,计算比较结果见表1。

表1 单侧阴极保护距离与阴极保护电流的计算结果

在该案例中,末端保护电流密度为3 μA/m2,始端保护电流密度为6 μA/m2,而利用式(24)计算得到平均电流密度为3.95 μA/m2。

4 关于公式的讨论

(1) 在目前常用的阴极保护长度计算公式[式(1)]中,ΔV的释义是“极限保护电位与保护电位之差”。比如,保护末端的极化电位达到-850 mV(相对于铜硫酸铜参比电极,下同),而保护始端的极化电位不超过-1 200 mV,以避免始端出现过保护。这样末端与始端的电位差ΔV为350 mV。该释义有待修正。

阴极保护范围的计算公式源自基于传输线理论的衰减公式。从衰减公式的原理来看,它可以计算管道对地的电位偏移,但无法计算管道的极化。极化取决于多个因素,比如电流密度、温度、氧含量、pH等,而衰减公式中无法考虑这些因素。

阴极保护范围计算公式的预设前提条件是阴极保护末端所选取的保护电流密度能使末端出现300 mV的电位偏移;为了避免过保护,阴极保护始端的电位偏移不超过600 mV(有时也取650 mV)。这样,始端和末端电位偏移的差就是300 mV或350 mV。虽然贝克曼的《阴极保护手册》以及相关标准[3]中,管道阴极保护范围计算公式(1)是正确的,但它对ΔV的释义是有误的。

(2) 衰减公式是在不考虑极化的状态下计算管道电位偏移和电流衰减的。在施加阴极保护的初期,极化效应不明显,阴极保护电流分布取决于电流路径的相对电阻;随着管道防腐层缺陷处阴极反应产物的积聚以及极化电位逐渐变负,衰减现象将得到缓解,阴极保护电流的分布将更均匀。

(3) 公式(1)和(22)的推导过程省略了高阶量,造成计算结果存在误差。公式(18)和公式(23)用于阴极保护范围和保护电流的计算时,比现行标准中提出的公式(1)、(22)和(3)具有更高的准确性。建议在相关标准中使用公式(18)和(23)替代公式(1)和(3)。

(4) 阴极保护范围和电流计算公式的准确性建立在多个前提假设之上:管道的防腐层绝缘性能是一致的,沿途土壤电阻率是均匀一致的,以及管道位于阴极保护辅助阳极的远地位置。如果管道处于辅助阳极的电场影响范围之内,则阴极保护的范围将缩短。

(5) 管道保护范围和阴极保护电流的计算准确性很大程度上取决于防腐层电阻率rC或阴极保护电流密度JCP的取值。在实际工程设计中,通常公式(1)中JCP的选值都较保守,高于管道末端出现300 mV电位偏移所对应的JCP,计算得到的保护范围偏保守。

此外,设计选取的阴极保护电源的输出有较大的调整余地,在一定程度上降低了对保护范围计算结果准确性的要求。

5 结 论

(1) 在目前常用的阴极保护长度计算公式[见式(1)]中,ΔV的释义有待修正。

(2) 公式(18)和公式(23)用于阴极保护范围和保护电流的计算时,比现行标准中提出的公式(1)/(22)和(3)具有更高的准确性。建议在相关标准中使用公式(18)和(23)替代公式(1)和(3)。

(3) 管道保护范围和阴极保护电流的计算准确性很大程度上取决于防腐蚀层电阻率rC或阴极保护电流密度JCP的取值。在实际工程设计中,通常公式(1)中保护电流密度的选值都较保守,计算得到的保护范围偏保守。