基于全变分加权差正则的高光谱图像去噪算法

钱 妍, 张 莉

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

随着遥感工作的不断深入,高光谱图像应用成为遥感领域研究热点之一。然而,受各种现实因素的影响,高光谱图像往往会受到各种噪声的污染[1],这不仅降低了图像的视觉效果,同时对后续应用,如目标检测、图像分类和场景识别等产生不良影响。因此高光谱图像去噪问题受到了众多学者的关注和研究。

近年来,针对含噪声的高光谱图像,学者们提出了很多高光谱图像去噪算法,并取得了较好的研究效果[2-15]。文献[2-3]使用传统的二维去噪方法对高光谱图像进行去噪,然而这种逐波段去噪方式往往会忽略相邻波段之间的相关性和一致性,导致去噪结果不理想。

为充分表征图像内部结构信息,适应更复杂的噪声环境,基于l1范数的全变分正则化(l1-spatial-spectral total variation,l1-SSTV)模型在去噪任务中受到广泛应用。文献[4]利用l1范数对图像梯度映射的基矩阵添加稀疏性约束,提出了增强型三维全变分(enhanced 3-D total variation,E-3DTV)模型;文献[5]将l1-SSTV模型与低秩先验相结合,提出低秩全变分(low-rank total variation,LRTV)模型;文献[6]利用l1-SSTV正则项模型恢复去噪的低秩图片块,形成低秩空谱全变分(spatial-spectral total variation regularized local low-rank matrix recovery,LLRSSTV)模型。然而,文献[7]发现l1-SSTV模型在去噪过程中会受到l1范数自身局限性的影响,在实际去噪过程中往往会产生伪影现象。

上述去噪算法主要存在以下3个缺陷：① 在复杂噪声环境下去噪效果不佳;② 恢复后的图像会产生一定的伪影;③ 优化低秩模型涉及奇异值分解,计算量大。本文针对上述去噪算法存在问题,提出了一种基于增强型三维全变分加权差(enhanced 3-D-l1-2total variation,E-3Dl1-2TV)正则模型的去噪算法。首先,利用l1范数与l2范数的全变分加权差(简记为l1-2)模型代替l1范数对图像稀疏性加以约束,避免由l1范数产生的伪影现象;同时,直接对梯度映射的基矩阵添加稀疏性约束,使得图像内部结构得到充分表征,适应复杂噪声环境。此外,本文算法在保证去噪效果较好的同时,在运算时间比上述方法具有明显优势。

1 预备知识

对于一个给定的高光谱图像χ∈Rh×w×s,其中,h、w、s分别表示高光谱图像空间高度、宽度以及光谱数量的大小。将χ沿着光谱方向展开得到矩阵形式的高光谱图像X∈Rhw×s。进一步地,将高光谱图像χ上沿第n个模方向计算的差分算子表示为Dn(n=1,2,3),分别对应于空间高度、宽度和光谱模方向。于是有：

gn=Dn(χ)

(1)

其中：gn∈Rh×w×s是沿3个张量模计算得到的梯度映射张量。将这些梯度映射张量沿着光谱模展开为矩阵形式：

Gn=unfold(gn), ∀n=1,2,3

(2)

易知χ上的差分算子D1和D2等价于X中行之间的减法运算,χ上的差分算子D3等价于在X中列之间的减法运算。上述3个线性运算可表示为：

nX=unfold(Dn(fold(X)))=Gn,

∀n=1,2,3

(3)

式(3)将高光谱图像X与其梯度影射Gn之间的关系进行编码,构建了关于梯度映射先验模型的高光谱图像处理方法。l1范数稀疏度量是最常用于计算梯度映射稀疏度的度量之一,即

S(Gn)=‖Gn‖1

(4)

在高光谱图像处理任务中,采用l1范数约束梯度稀疏性的三维全变分(3DTV)正则化模型通常表示为：

(5)

2 本文算法

2.1 增强型全变分正则模型

对于给定的高光谱图像X∈Rhw×s,沿着其梯度映射施加稀疏度度量可表示为STV(Gn),其中,Gn=nX,∀n=1,2,3。基于展开的高光谱图像具有低秩性质这一前提,Gn可表示为：

(6)

其中：Un∈Rhw×r;Wn∈Rs×r;r为高光谱图像矩阵的秩。Un中的列构成梯度映射Gn的一组基。同样,式(6)中Un也可以看作为Gn经过变换得到的结果,即

(7)

与沿图像梯度映射施加稀疏约束不同,本文对Gn的线性变换结果,即GnVn,采用l1范数稀疏度量约束,构建增强型全变分模型,表示为：

(8)

式(8)对Vn采用2个必要的约束：① 对变换结果GnVn施加Frobenius范数约束,避免变换引起的信息丢失;② 对Vn施加正交约束,保证变换结果GnVn更充分地保留其原始梯度映射Gn的内部结构信息并且获得封闭解。直接求解式(8)并不容易,因此将其改写为：

(9)

2.2 增强型三维全变分加权差正则模型

与式(5)中3DTV正则化模型类似,本文通过沿不同模的梯度映射稀疏度量值求和,对增强型三维全变分正则化进行建模：

(10)

式(10)等价于：

(11)

由于l1范数自身的局限性,基于3DTV正则模型的去噪算法往往会产生伪影。考虑到全变分加权差正则化(l1-2TV)模型在自然图像去噪中的优越表现,将式(11)中‖Un‖1替换为f1-2(Un),其中f1-2(Un)=‖Un‖1-α‖Un‖2。于是增强型全变分加权差(E-3Dl1-2TV)正则模型可表示为：

(12)

2.3 基于E-3Dl1-2TV正则模型去噪算法

基于E-3Dl1-2TV正则模型的高光谱图像算法表示为：

s.t.Y=X+E

(13)

其中：Y、X、E∈Rhw×r分别为输入的噪声图像、待恢复的图像以及稀疏噪声;τ为正则项与噪声稀疏项之间的平衡系数。由式(12)可得,目标函数式(13)的等价形式可写为：

(14)

其中：Vn∈Rs×r;Un∈Rhw×r;n=1,2,3。

3 模型求解

模型式(14)利用交替方向乘子(alternating direction method of multipliers,ADMM)算法[16]求解。引入拉格朗日乘子Mn(n=1,2,3)、Γ以及参数μ,对应的增广拉格朗日方程为：

L(X,E,Un,Vn,Mn,Γ)=

(15)

保持其他变量固定不变,交替优化式(15)中每个变量,下面讨论解决相关变量的子问题。

3.1 更新变量X

关于式(15)中的X变量,可得到如下线性等式：

(16)

采用快速傅里叶变换求解方程,得到X的闭式解如下：

(17)

其中：1表示元素全为1的张量;⊗为逐元素相乘运算;F(·)表示傅里叶变换;|·|2表示逐元素平方运算。

3.2 更新变量Un

从式(15)中提取所有含Un的项可得：

(18)

求解式(18)前需要利用DCA算法[17]对其线性化处理,令

E(Un)=G(Un)-H(Un)

(19)

其中

G(Un)=‖Un‖1+

(20)

H(Un)=α‖Un‖2

(21)

于是,式(18)可重写为：

(22)

由软阈值算法[18]求解得：

(23)

3.3 更新变量Vn

从式(15)中提取所有含有Vn的项可得：

(24)

计算出封闭解：

(25)

3.4 更新变量E

从式(15)中提取所有含有E的项可得：

(26)

软阈值算法求解：

(27)

基于一般的ADMM算法原理,拉格朗日乘子更新可得：

(28)

综上,基于E-3Dl1-2TV的去噪模型优化过程全部完成。

4 实验结果与分析

为验证E-3Dl1-2TV算法的去噪性能,设计了仿真实验和模拟实验2类实验。选取现有4种去噪算法(文献[4]、文献[5]、文献[8]、文献[9])作比较。仿真实验中Indian-s数据集的大小为145×145×175,真实实验中HYDICE Urban数据集大小为207×207×210。

在仿真实验过程中,本文设计4种加噪方案模拟噪声环境,具体如下：

方案1 高斯噪声(SNR=10～20 dB)被添加到每个波段。

方案2 在方案1基础上,在每个波段添加10%的脉冲噪声,并在4个随机波段中分别添加4条水平和垂直的死线噪声,宽度在1～3个单位宽度中生成。

方案3 方差范围在0.1～0.2随机选择的零均值高斯噪声添加到每个波段。

方案4 在方案2基础上,在每个波段添加10%的脉冲噪声,在波段61～71中分别随机添加1～10条死线噪声,宽度在1～3个单位中随机生成。

Indian-s数据集中所有算法的客观评价结果见表1所列。表1中：MPSNR (mean peak signal-to-noise ratio)为平均峰值信噪比;MSSIM (mean structural similarity)为平均结构相似性;ERGAS (erreur relative globale adimensionnelle de synthèse)为相对维度综合误差;MSA (mean spectral angle) 为平均光谱角度。从表1可以看出,本文算法E-3Dl1-2TV的定量结果均优于其他去噪算法。

表1 Indian-s数据集的定量对比结果

方案1与方案2下每个波段对应的PSNR值如图1所示。从图1可以看出,与E-3DTV相比,E-3Dl1-2TV指标分数更高,表明了全变分加权差模型在图像恢复中的有效性,这也是本文所提出算法的核心思想。

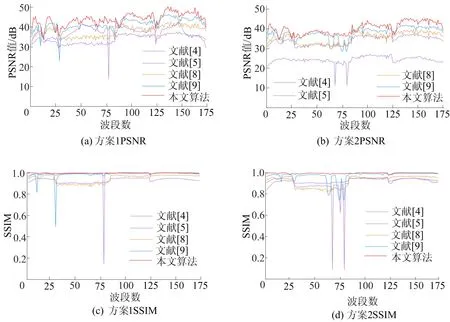
图1 加噪方案1和方案2下5种算法去噪各波段PSNR与SSIM结果

加噪方案2下Indian-s数据集第70波段在5种去噪算法下的去噪结果如图2所示。由图2可知,通过局部放大细节可以看出,E-3Dl1-2TV获得最佳视觉效果,有效去除了噪声并完全保留了原本图像中的边缘结构,而其他算法均有不同程度的丢失。

图2 加噪方案2下第70波段对应的5种算法的恢复结果

为了更加直观地验证E-3Dl1-2TV混合噪声消除的能力,第70波段的噪声图像去噪前后的垂直平均轮廓曲线如图3所示。从图3可以看出,E-3Dl1-2TV的轮廓曲线最接近干净图像曲线,与图2所示的视觉对比度一致。总体而言,与其他算法相比,E-3Dl1-2TV不仅有效去除了混合噪声,还完整保留了图像结构。

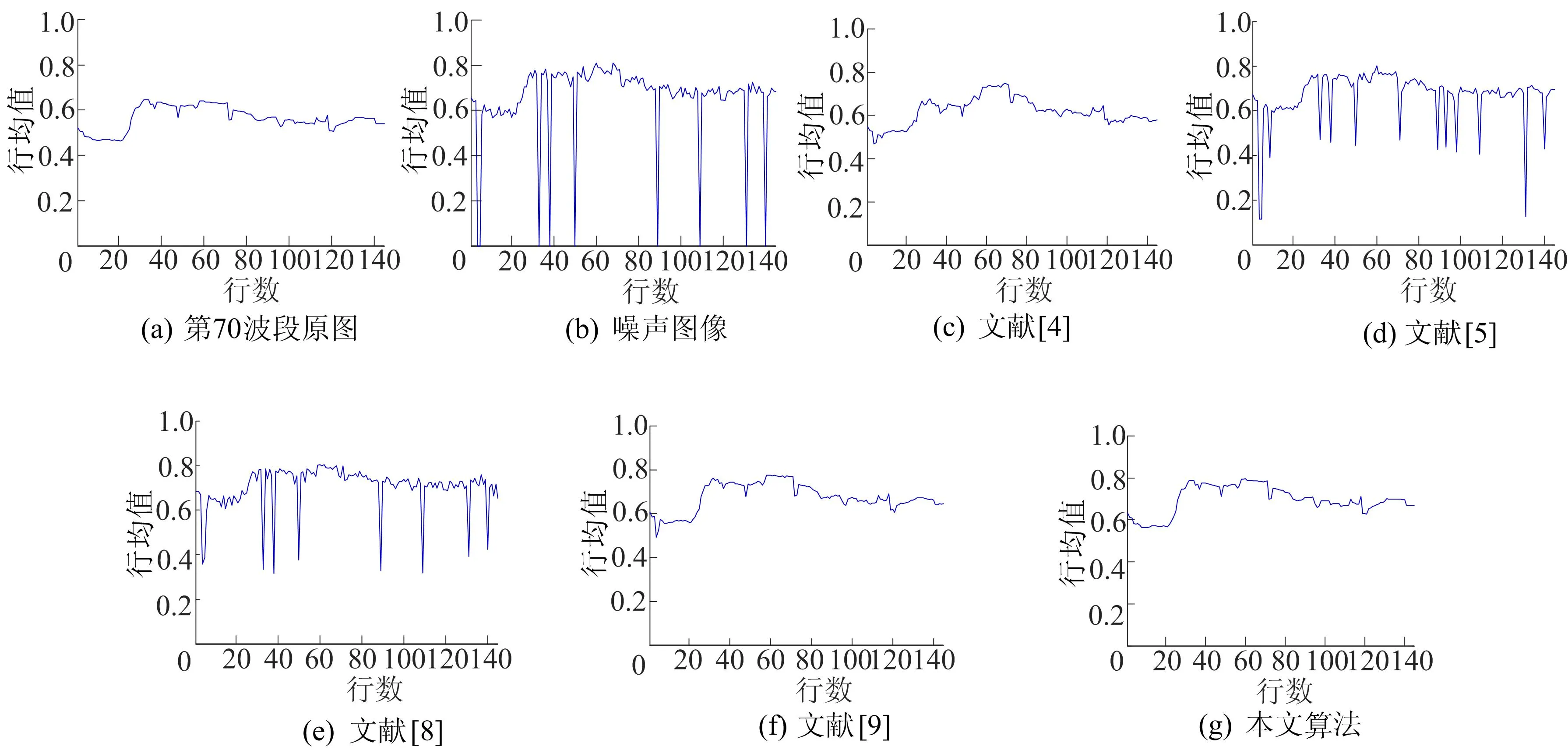
图3 加噪方案2下第70波段对应的5种去噪算法的垂直平均轮廓曲线

在真实数据集实验中,一方面通过对比真实数据集Urban恢复图像的视觉效果评价各方法的去噪性能;另一方面对真实数据集Indian-Pines的恢复图像进一步施加分类实验,通过分类视觉效果和量化指标结果进一步对比恢复图像的质量。

Urban数据集第139波段的原始噪声图像和不同算法的去噪结果如图4所示。观察局部放大部分,E-3Dl1-2TV得到的恢复图像具有更加清晰的边缘,条纹噪声的去除更加彻底,保留了更多空间细节。其他算法的恢复结果要么显得过于平滑,要么条纹噪声仍然存在。第139波段的原始图像及其不同去噪图像的垂直平均轮廓曲线如图5所示。

图4 Urban数据集第139波段在5种去噪算法下的恢复结果

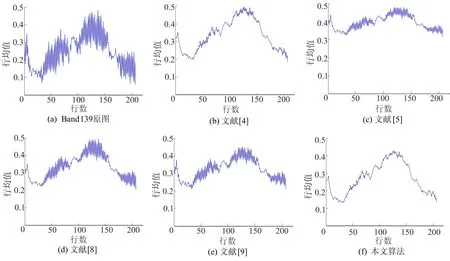
图5 Urban数据集第139波段在5种去噪算法下的垂直平均剖面

尽管均值曲线在恢复后出现不同程度平滑,但BM4D、LRTDTV和TLR-l1-2SSTV算法对应的曲线仍存在较大的波动,表明噪声未完全消除。相反,E-3Dl1-2TV获得更平滑的曲线,表明其降噪能力优于其他算法。

对Indian Pines采用不同方法进行去噪,并将所得的恢复图像进一步施加分类实验,分类结果如图6所示。实验结果表明,去噪算法对图像后续应用具有一定提升效果,并且E-3Dl1-2TV得到最清晰的分类结果。各算法分类实验的客观评价结果见表2所列。表2中：OA (overall accuracy) 指标代表整体精度;kappa系数用来衡量2个变量一致性。

图6 IndianPines 数据集在五种方法去噪后的分类实验结果

表2 Indian-Pines数据集分类实验评价指标

对比结果表明,E-3Dl1-2TV取得了最高指标分数,进一步说明了E-3Dl1-2TV在去噪性能上的优越性。

5 结 论

针对现有基于全变分正则模型的高光谱图像去噪算法中出现的伪影、边缘细节丢失等问题,本文改变了传统全变分模型约束对象,并使用一种新的约束度量,提出增强型的三维全变分加权差正则化(E-3Dl1-2TV)模型。该模型对梯度映射的基矩阵添加稀疏性约束,并使用加权差模型作为稀疏性度量,有效抑制了去噪过程中伪影的产生。实验结果表明,相比一些主流的去噪算法,本文算法所得到的图像能保留更多的图像细节。