基于深度复数神经网络的雷达目标DOA估计算法
2024-02-03朱安琪项厚宏齐美彬
朱安琪, 项厚宏, 齐美彬
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.合肥工业大学 计算机与信息学院,安徽 合肥 230601)
波达方向(direction of arrival,DOA)估计在雷达、通信、宇航等领域有着广泛的应用,且是阵列信号处理的重要研究方向[1]。在雷达阵列信号处理领域中,经典有效的物理模型驱动算法包括多重信号分类算法(multiple signal classification,MUSIC)[2]、最大似然估计算法(maximum likelihood,ML)[3]、旋转不变子空间算法(estimation of signal parameter via rotational invariance techniques,ESPRIT)[4]和以贝叶斯学习的稀疏感知算法[5-6]等。物理模型均是在一定先验条件下得到,如入射信号满足远场、近场或混合场等物理条件[7-8],在不同的条件下,各算法的估计表达式又存在较大不同,而且当阵列存在多种非理想因素(如阵列误差等)时,物理驱动的算法估计性能会急剧下降,甚至无法准确估计。
随着深度学习技术在信号处理领域的广泛应用,基于深度神经网络的数据驱动的DOA估计算法也在持续推进。目前数据驱动的DOA估计算法主要分为3大类:第1类是端到端的DOA估计算法[9-11],将DOA估计问题建模成高维非线性映射模型,直接学习阵列接收数据与DOA的映射关系,进而实现DOA估计,此类学习模型简单,直接从阵列接收数据中挖掘DOA信息,但缺少应用阵列先验信息(如方位、地形等),阵地适应性一般;第2类是将DOA估计问题建模成分类问题[12-13],由于DOA信息具有空域稀疏性,将DOA信息构造成独热编码形式,通过学习阵列接收数据到DOA的分类网络,从而实现DOA估计,虽然分类模型比较成熟,但是DOA估计问题本质上是回归问题,若以一定的角度将整个空域划分成多个标签,则必然会存在细微的模型误差,测角性能受限于划分角度;第3类是重点考虑阵列接收数据中的相位特征[14-16],通过增强期望信号的相位特征,实现期望信号增强,非期望信号抑制的效果,进而提高DOA估计精度。这3类深度学习的DOA估计算法均训练阵列接收的复数据的部分实数特征或者实数化,对于复数域的线性映射模型来说[17-18],学习部分实数特征或者实数化处理复数据显然不能有效学习全域特征或者增大学习复杂度。
本文构建复数域的深度神经网络模型,学习阵列接收带噪复数据与理想无噪的标签数据的映射关系,实现期望信号特征增强和非期望信号削弱的效果,最后利用经典的物理驱动算法数字波束形成(digital beam forming,DBF)和多重信号分类算法(multiple signal classification,MUSIC)算法进行DOA估计。
1 信号模型
假设阵列结构为M阵元的均匀线阵,阵元间距为d,K个相互独立的远场窄带入射信号s(t)=[s1(t)s2(t) …sK(t)]T,其方向向量θ=[θ1θ2…θK]T,信号波长λ,则阵列在t时刻的数据y(t)=[y1(t)y2(t) …yM(t)]T可表示为:
(1)

E(n(ti),n(tj))=σ2Iδti,tj
(2)
其中:I表示单位矩阵;δti,tj表示冲激函数。且信号源与噪声互不相关,即
E(n(ti),s(tj))=0
(3)
假设信号源之间互不相关,则有:
E(s(ti)sH(tj))=diag(p)δti,tj
(4)
其中:p=[p1p2…pK]T为K个信号源的功率矢量。当阵列接收到L个快拍数据时,阵列接收数据记为Y=[y(t1)y(t2) …y(tL)]∈CM×L,信源数据记为S=[s(t1)s(t2) …s(tL)]∈CK×L,噪声数据记为N=[n(t1)n(t2) …n(tL)]∈CM×L多快拍条件下,阵列接收数据模型可以表示为:
Y=AS+N
(5)
阵列接收数据协方差矩阵为:
(6)
在实际工程中,数据协方差矩阵以采样协方差矩阵代替,即
(7)

(8)
已有的物理驱动的超分辨DOA估计算法有DBF算法、MUSIC算法和ML算法,其估计表达式可总结为:
(9)
(10)
(11)
其中:UN为噪声子空间;PA(θ)为投影到阵列流型矩阵A(θ)张成的信号空间的投影算子。通过搜索,实现对目标角度的估计。根据3个算法的估计表达式,消除协方差矩阵误差和噪声数据协方差矩阵,才能有效提高期望信号的信噪比,提高DOA估计算法精度。观察阵列接收数据模型,阵列接收数据y(t)为K个阵列导向向量的线性组合,目标角度θ或a(θ)与阵列输出数据y(t)为线性映射关系。
若采用复数神经网络(complex-valued neural networks,CVNN),则能极大减小学习难度且更有效,因此本文提出一种基于复数神经网络的DOA估计算法,通过构建复数神经网络,增强期望信号数据,削弱噪声等非期望信号,最后采用经典的超分辨算法实现DOA估计。
2 复数神经网络的DOA估计算法
本文提出的复数神经网络的DOA估计算法系统框图如图1所示。在训练部分,对阵列接收数据进行归一化预处理,并构建复数神经网络,通过大量多快拍数据,学习阵列接收到的单个快拍数据与理想无噪数据的映射关系。在增强部分,首先结合训练部分的归一化参数对测试数据进行归一化预处理;然后输入训练好的复数神经网络,并用归一化参数对输出数据进行反归一化预处理,得到增强后的阵列数据;最后采用已有的物理驱动算法进行DOA估计。

图1 基于复数神经网络特征增强的DOA估计算法框图
2.1 复归一化预处理
实际阵列采集数据的信噪比随着目标的空间状态、位置的改变而存在较大起伏,其直接表现在脉压后数据的实虚部值变化较大,因此在特征提出过程中,输入特征变化较大会导致协变量偏移现象。复归一化预处理是输入复数神经网络前的一次预处理,利用优化改变方差大小和均值位置,使得新的分布更契合数据的真实分布,保证模型的非线性表达能力。复归一化预处理算法将实部和虚部分开,分别看成2个不同维度,具体计算公式为:
(12)
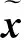
(13)
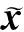
(14)
crr+cii+j(cir-cri)
(15)
crr-cii+j(cir+cri)
(16)
2.2 复前向传播
对于复归一化预处理后的输入数据,采用栈式神经网络模型,即每个隐含层均与前一层的所有神经元相连接,做线性处理和非线性激活后输出。对于第q层复数神经网络,其网络的输出可以表示为:
(17)
其中:oq和oq-1分别表示第q层的输出和输入数据,且o0为复数神经网络的输入;Wq和bq分别表示第q层的复权值矩阵和复偏置矢量;f(x)表示复激活函数,直接决定反向传播(backpropagation,BP)算法的非线性拟合性能和收敛性。
通常,复激活函数是可解析和有界,即需要满足柯西-黎曼方程。现有研究中常用的复激活函数有Csigmoid、Ctanh、modReLU、zReLU和CReLU等,已有文献验证了CReLU不仅满足柯西-黎曼方程,而且非线性映射性能更优,在网络层数较多的情况下,能够尽可能地保留更多的有用信息。因此,本文采用CReLU复激活函数,其等价于采用ReLU激活函数分别处理实部和虚部,其计算表达式为:
CReLU(x)=ReLU(Re(x))+jReLU(Im(x))
(18)
2.3 CVNN的复反向传播与参数更新
CVNN的监督训练时优化复权矩阵和复偏置矢量,使得网络输出与标签值相匹配,本文采用复均方误差(complex mean square error,CMSE)为损失函数,其定义方式为:
(19)

通过最小化CMSE,优化、更新复数神经网络的复权矩阵和复偏置矢量,即
(20)
本文采用随机梯度下降算法更新网络的复权值矩阵和复偏置矢量,其迭代过程可以表示为:
(21)
(22)
其中:vWt+1和vWt分别表示t+1次和t次的复值权重的速度矢量,初始状态为0;vbt+1和vbt分别表示t+1次和t次的复值偏置矢量的速度矢量,初始状态为0;μ∈[0,1]表示动量常数;η表示学习率;dW和db分别表示复权矩阵和复偏置矢量的梯度。
3 实验仿真和分析
本节通过计算机仿真实验,分析不同信噪比和快拍数下所提算法的估计精度及泛化性。假设阵列接收为15阵元的均匀线阵,阵元间距半波长,批大小为100,学习率为10-5,动量常数为0.9。假设存在2个相干源,θ1∈[-3°,0°],θ2∈[5°,8°],此时1个波束宽度以内和1个波束以外均存在样本,保证样本的多样性。本文对比CVNN增强前后各算法的测角均方根误差(root mean square error,RMSE),展示增强前后的空间谱,分析所提算法的有效性和可靠性。测角均方根误差定义公式为:
(23)

3.1 信噪比对估计精度的影响
设快拍数为10,训练集样本的信噪比为0~10 dB,信噪比间隔为2 dB;测试集样本的信噪比与训练集样本完全匹配。以蒙特卡洛方法生成样本,训练集的蒙特卡洛次数为105,测试集的蒙特卡洛次数为2×103。DBF、MUSIC和ML算法在CVNN增强前、后的测角均方根误差与信噪比的关系曲线如图2所示。
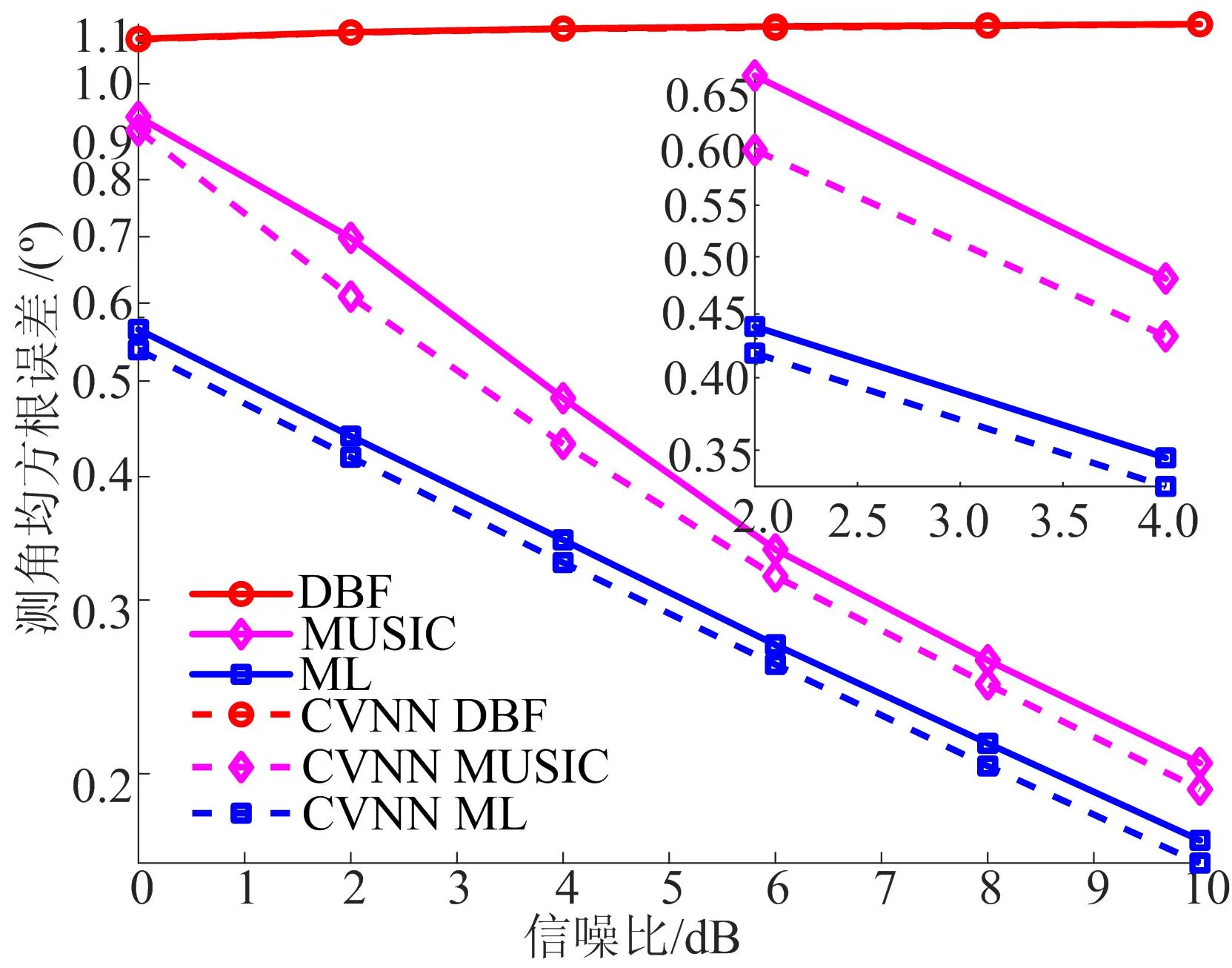
图2 测角均方根误差与信噪比关系曲线
从图2可以看出:DBF算法在增强前、后性能均较差,不能准确测角,这是由于θ1和θ2在一个波束宽度内,而DBF不能突破瑞利线;而增强后的MUSIC算法和ML算法的效果更优,误差更小。
以ML算法为分析对象,若以信噪比为参考指标,经过CVNN增强后,随着信噪比的增大,测角均方根误差由0.53°下降至0.16°,其接收数据的等效信噪比约提高了1 dB。随机抽取一个样本,信噪比在0~10 dB时的MUSIC空间谱分析结果如图3所示。
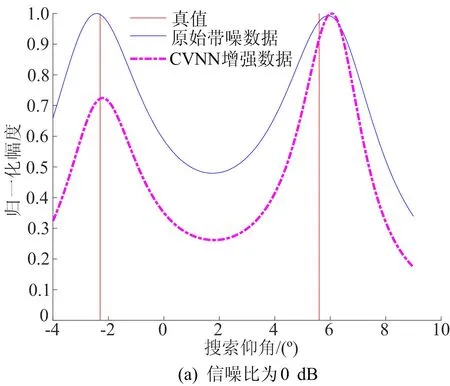
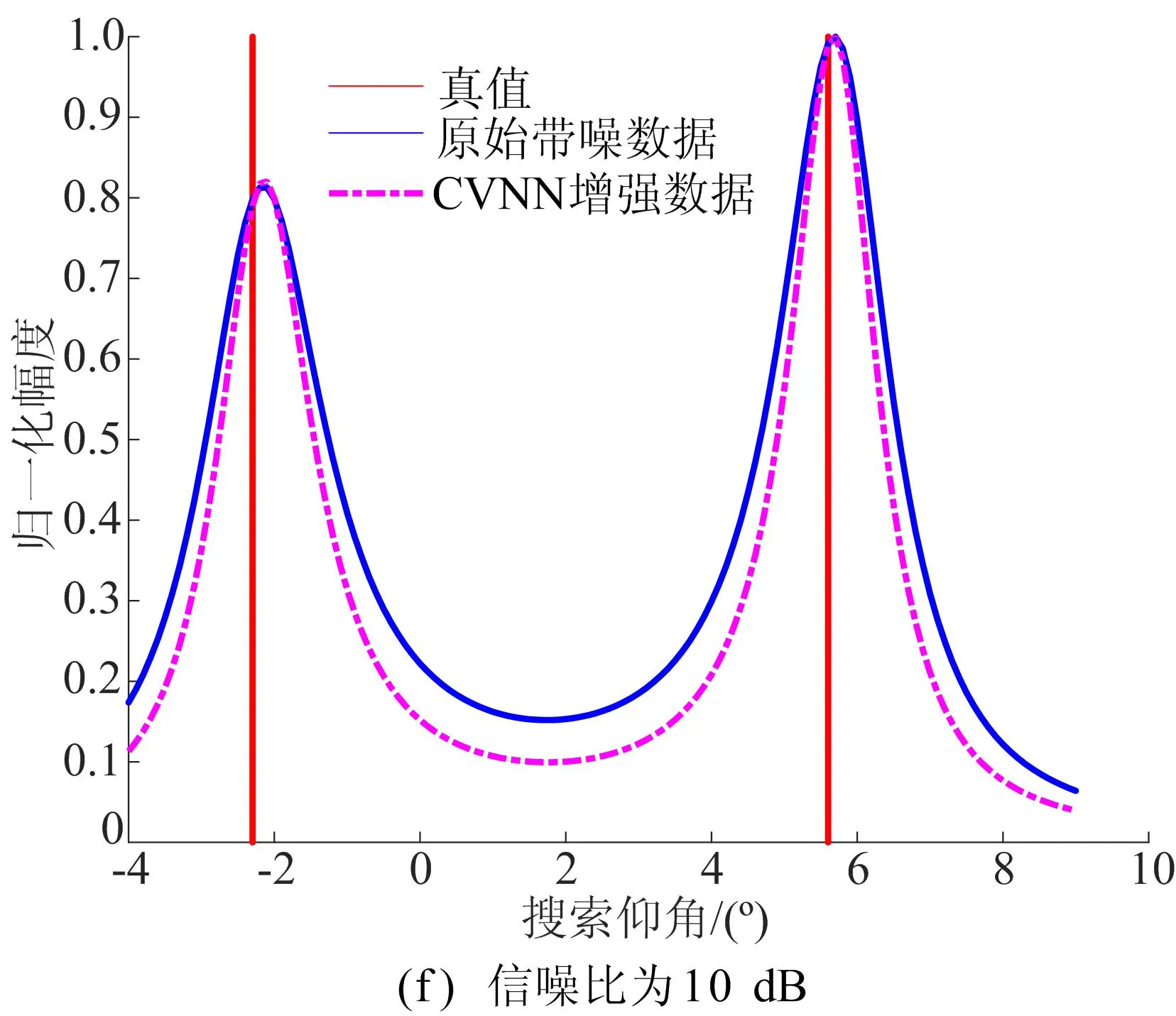
图3 MUSIC算法空间谱分析
从图3可以看出,信噪比越大,MUSIC算法空间谱的谱峰越尖锐,测角误差越小,且经过CVNN增强后,MUSIC算法的谱峰更尖锐,且测角误差更小。因此,本文算法在匹配信噪比条件下测角性能更佳,且具有良好的噪声抑制能力。
3.2 算法对信噪比的泛化性
本节分析算法对信噪比参数的泛化性,即训练集和测试集样本的信噪比不完全匹配时,所提算法的测角精度。本节的仿真参数与3.1节保持一致,但测试集的信噪比范围为-1~13 dB,与训练集样本的信噪比差异始终存在1 dB以上的差异。不同信噪比条件下所提算法的估计精度如图4所示。
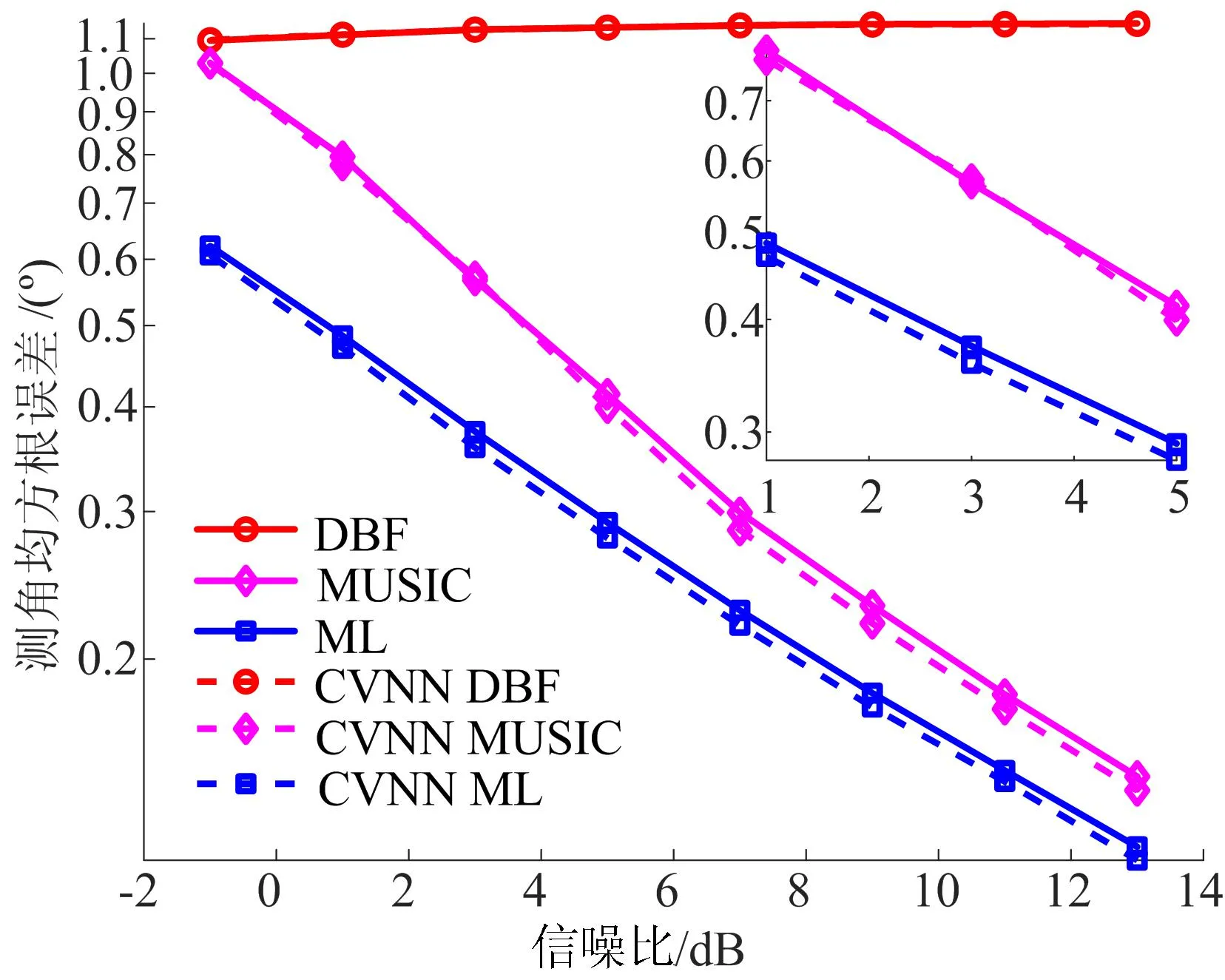
图4 所提算法对信噪比的泛化性分析
由图4可知,即使训练集和测试集信噪比参数不完全匹配,所提算法仍然可以有效测角,且测角性能较已有算法有所提升。以ML算法作为分析对象,随着信噪比的增大,测角均方根误差由0.6°下降至0.11°。综合分析结果可知,所提算法具有良好的估计性能和泛化性。
3.3 快拍数对估计精度的影响
本节分析快拍数对所提算法性能的影响。阵列结构参数与上述各节一致,训练集和测试集的信噪比均为0 dB,测试集的快拍数为10~25,不同快拍数的测角均方根误差如图5所示。

图5 测角均方根误差与快拍数的关系
由图5可知:经过CVNN增强后,ML算法的测角误差由0.54°下降至0.34°;MUSIC算法的测角误差由0.91°下降至0.51°。算法性能均优于增强前的各类算法。若以快拍数作为评价指标,经过CVNN增强后,数据的等效快拍数提高了3。因此,所提算法适用于多快拍场景,且性能较优。
4 结 论
本文提出了一种基于CVNN的目标DOA估计算法,通过构建复数神经网络,直接训练阵列接收复数据,实现期望信号增强和非期望信号抑制的效果,进而提高DOA估计精度。大量仿真实验表明,经过CVNN增强后,传统算法的估计效果有一定的提升,模型可解释性更强。
