滑坡易发性预测建模的不确定性:不同“非滑坡样本”选择方式的影响
2024-02-02黄发明曾诗怡熊浩文范宣梅黄劲松
黄发明,曾诗怡,姚 池*,熊浩文,范宣梅,黄劲松
(1.南昌大学工程建设学院,江西南昌 330031;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川成都 610059;3.纽卡斯尔大学岩土科学与工程卓越研究中心,纽卡斯尔 2287)
滑坡对生命和财产造成的破坏十分严重且影响范围较大[1–2]。滑坡易发性预测作为滑坡风险评估的基础非常重要,在GIS和机器学习等技术快速发展的背景下,利用多学科交叉融合方式开展滑坡易发性建模已成为滑坡风险评估的有效工具之一[1,3–4]。
当前,滑坡易发性建模(LSP)过程主要包括获取滑坡编录与环境因子、划分模型训练/测试集、确定合适的机器学习模型、分析预测结果的不确定性等步骤[5]。其中,存在各种影响建模结果的不确定性,例如数据测量、不同联接方法、不同数据驱动模型的不确定性等等,已有研究分析了部分因素的不确定性[6–8]。根据机器学习建模原理可知,由滑坡和非滑坡样本共同组成的训练/测试集作为机器学习的核心在整个建模过程中至关重要。其中滑坡样本通常根据历史滑坡编录或遥感影像及航片进行选取,其存在的不确定性较小[9–10]。而非滑坡样本通常无法直接获取,文献显示大多通过采集“伪”负样本来代替非滑坡样本且目前没有统一的选择方式[11–13]。因此,非滑坡的选择相对于滑坡样本而言不确定性更大,是影响模型训练/测试集质量的关键因素之一,合理地选择可信度高的非滑坡样本有利于降低建模不确定性[11]。
现有研究大多在整个研究区内未发生滑坡的区域中随机选择非滑坡样本[14–15]。一般而言,滑坡在河道、沟谷等低坡度区域内发生的概率较小,因此,可利用高分辨影像解译低坡度属性区并从中随机选择非滑坡[16–17]。此外,缓冲区控制采样法也常应用于滑坡易发性预测,即从滑坡面缓冲区以外的区域选择非滑坡样本[11,13,18]。对于上述非滑坡选择方式,全区随机选择虽然避开了已知滑坡点,但是难以保证非滑坡样本的可靠性,导致样本误差较大,进而将误差传递给了易发性建模。从低坡度属性区中选择虽然改善了非滑坡的稳定性,但使采样工作被坡度因子主导。另外缓冲区外选择非滑坡对缓冲半径的确定并无统一标准,缓冲区过大或过小均会造成建模的不确定性,且采集的滑坡点不同将影响缓冲区的位置从而改变选择范围[11]。
信息量(IV)法和半监督法选择非滑坡样本的原理类似,即极低和低易发区内发生滑坡概率较小,在此范围内选择非滑坡样本的可靠性更高[9,19]。信息量法不需要非滑坡样本也能得到初始滑坡易发性分区[20]。半监督法结合了全监督和无监督的优点,在仅有少量已标记样本的情况下能够利用隐藏在大量无标签样本中的数据分布信息来提升学习性能[21]。
综上所述,由于上述各类选择方式的主观性和随机性较强,导致获取的非滑坡样本不具有足够的代表性,降低测试集的质量,从而影响后续建模性能。本文以江西省南康区为例,采用5种非滑坡样本选择方式,即全区随机选择[14]、坡度小于5°的特定属性区内随机选择[16]、滑坡面缓冲300m外随机选择[11]、信息量法[20]以及半监督法[21];将得到的非滑坡样本与机器学习耦合构建模型预测易发性;对比5种方式的易发性结果,进而探究不同非滑坡选择方式对建模不确定性的影响规律;比较不同机器学习的应用效果,发现随机森林(RF)所需输入参数和调整较少,且预测精度较高[8,22–23];故最终构建随机RF、低坡度RF、缓冲区RF、IV–RF和半监督RF模型进行易发性预测。
1 滑坡易发性预测建模方法
1.1 研究思路
本文构建随机RF、低坡度RF、缓冲区RF、IV–RF和半监督RF模型开展易发性建模并对比分析。具体流程如图1所示:1)获取研究区滑坡编录信息并采集19种基础环境因子数据,利用频率比相关性分析得到各因子的值;2)基于环境因子相关数据,利用IV模型、随机RF模型进行初始易发性分区,将极低和低易发区作为选择范围获取高可靠性的非滑坡样本;3)合并获得的非滑坡样本与历史滑坡样本,耦合构建随机RF、低坡度RF、缓冲区RF、IV–RF和半监督RF模型进行易发性预测;4)对比5种选择方式耦合的RF模型的预测结果,采用ROC(receiver operation characteristic curves)曲线和易发性指数分布规律分析建模不确定性,并探讨半监督RF模型中样本非对称的情况。
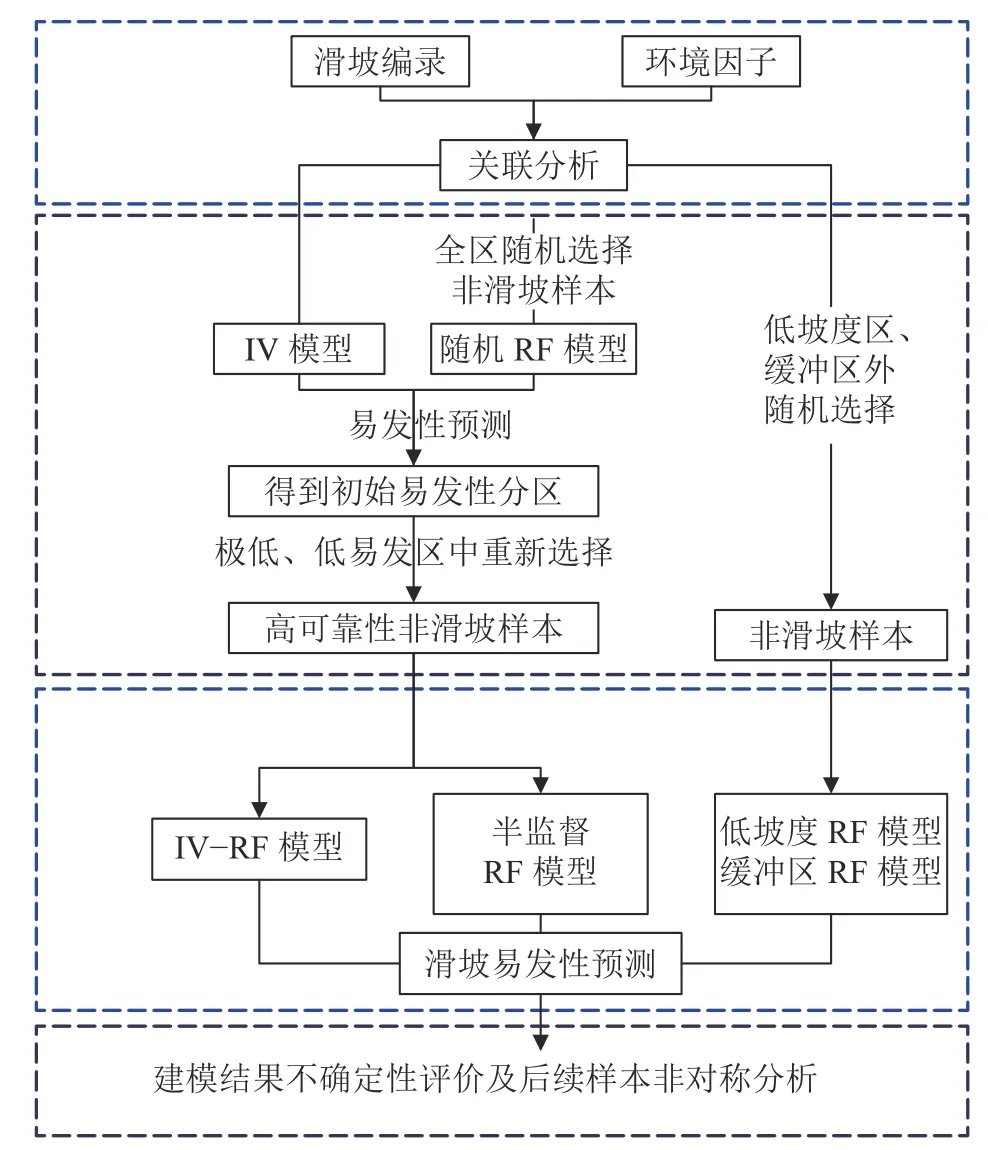
图1 不同非滑坡样本选择方式的滑坡易发性预测建模流程Fig. 1 Flow chart of LSP modeling under different non–landslide sample selection methods
1.2 非滑坡样本选择
全区随机选择时先剔除整个研究区内的已知滑坡区域,从得到的无滑坡区中随机选择非滑坡样本[14]。从低坡度区域选择时根据研究区的坡度特征设置合理的坡度值,筛选出坡度小于该值的区域后从中随机选择单元作为非滑坡样本[16]。结合研究区地理环境以及历史滑坡信息确定缓冲距离的大小后基于历史滑坡面数据利用ArcGIS 10.2创建滑坡缓冲区,选择整个研究区缓冲区以外的区域作为非滑坡样本的选择范围[11]。
信息量法选择非滑坡首先利用信息量模型计算获得各环境因子的信息量值,对其进行叠加后得到总信息量值[20]。在A rcGIS 10.2中运用自然断点法对全区总信息量值进行初始分区。由于信息量值越高表明发生滑坡的概率越大,在极低、低易发区内进行非滑坡样本的选择。
在全区随机选择非滑坡进行易发性建模的基础上建立半监督法。由于初始预测得到的极低、低易发区内的栅格单元发生滑坡易发性小,在此区域内进行非滑坡样本的采集更加合理,提高了非滑坡样本的可信度。
1.3 随机森林(RF)模型
RF模型基于决策树算法通过独立采样和随机选择特征变量构建多个决策树模型进行预测和分类得到综合分析结果[22]:1)从原始训练集样本中进行有放回的重复采样以获得与原始样本特征数目相同的样本,作为决策树根节点处训练集;2)从N个特征中随机选取n个(n≪N)为决策树节点的分裂建立特征集并择取其中一个作为某节点的分裂属性;3)决策树上每一节点按2)中进行分裂并建立此类大量决策树形成随机森林[8]。由于建立一组决策树进行预测会产生泛化误差的限制值,使用RF模型能有效避免模型过拟合问题的出现,显著提高模型的有效性和优越性[20]。
1.4 滑坡易发性建模不确定性评价
1.4.1基于ROC曲线的精度分析
采用ROC曲线分析易发性建模精度,能有效降低因测试集差异而产生的干扰,使模型性能评估工作更客观[24]。由式(1)~(2)计算的真阳性率(RTPR)和假阳率(RFPR),分别代表分类器识别滑坡的准确程度[22]:
式中,nTP、nFN分别为被正确识别为滑坡的滑坡点个数和被错误识别为非滑坡的滑坡点个数,nFP、nTN分别为被错误识别为滑坡的非滑坡点个数和被正确识别为非滑坡的滑坡点个数。结合ROC曲线下面积SAUC对模型进行量化分析,反映出随机挑选的结果中滑坡样本排名高于非滑坡样本的概率[8]。SAUC值一般在0.5~1.0范围内,越接近1.0,说明该模型的预测性能更优越。利用式(3)计算SAUC:
式中,n0、n1分别为非滑坡与滑坡样本个数,ri为第i个非滑坡样本在整个测试样本中的排序。
1.4.2基于混淆矩阵的精度评价
基于混淆矩阵衍生得到的Kappa系数(KC)和总体分类精度(OA)是滑坡易发性模型精度评价的重要指标。Kappa系数通常用于一致性检验,而总体分类精度能够直接反映模型分类正确的比例,由式(4)~(5)计算得到:
式(5)中,KC系数值通常在0~1.0范围内。当KC在0.6~1.0时,则说明模型具有高可靠性;当KC大于0.8时,说明预测结果与实际较一致[20]。Pe为期望一致率,即两次检验结果由于偶然机会所造成的一致率:
1.4.3滑坡易发性指数分布
滑坡易发性指数分布特征主要通过均值和标准值两个指标进行分析,二者分别反映了易发性指数分布的平均水平和离散趋势[20]。均值较小,表明极低和低易发区包含了大部分易发性指数,结合高SAUC精度,进一步表明此时建模的不确定性更小;标准差大,说明整体易发性指数的分散程度高,结合高SAUC精度,进一步表明滑坡易发性指数的可识别性强,且与野外滑坡实际分布情况更契合[25]。
2 研究区概况及环境因子选取
2.1 南康区概况及其滑坡编录
如图2所示,南康区地处江西省赣州市西部,属中亚热带季风湿润气候。年均降雨约1443.2mm,雨量充沛但分布不均,境内水资源丰富。地处山脉区间高度范围为96~995m,呈纵长横狭之势,总面积约1844.96km2。地形地貌以丘陵、山地为主,且章江、上犹江两岸分布有较平整的河谷平原。根据南康区自然资源部门所知,1970—2010年累计发生约233处滑坡。当地滑坡以中小型规模为主,大部分为牵引式滑坡,滑体主要是第四纪堆积层。滑坡空间分布较均匀,北部和南部的低山、高丘陵山区、中部低丘陵区(红层盆地)为滑坡多发区,其中地层界线交界处、道路两侧及植被分布较少的区域分布有较多滑坡。而在受人类活动影响较小的植被丰富地区滑坡数量更少,如镜坝—三江—龙华河谷阶地。为避免原始滑坡点的空间位置误差引起建模不确定性,在绘制滑坡样本的边界时将边界向外合理且尽可能准确地扩展。相关文献综述表明南康区内诱导滑坡发生的主要原因是强降雨,其次人类活动也对滑坡的发生具有一定的影响[21]。
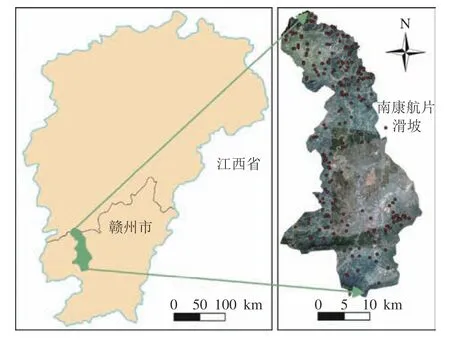
图2 南康区概况及滑坡编录Fig. 2 Overview of Nankang District and landslide inventory
2.2 数据源
研究采用的数据源主要包括:1)南康区自然资源局历史滑坡编录资料及地质勘察报告;2)30m分辨率的数字高程模型(DEM)用于获取地形地貌和水文环境等环境因子;3)采用1∶105比例尺的地质图提取岩性因子;4)采用30m分辨率的La n d s a t TM 8遥感影像1景(2013.07.03,轨道号119/041)提取地表覆被因子;5)从中国科学院地理数据贡献平台获取研究区的年均降雨量、人口密度、GDP等数据用于提取相关环境因子。本文采用30m的分辨率表达DEM和遥感影像,符合国家基础空间数据库的建库标准且能有效反映地形地貌特征,同时能够避免出现因栅格数过多造成模型计算困难的问题[26]。最终将233个滑坡编录划分成2 598个滑坡栅格单元,即易发性建模时共有2 598个滑坡样本。
2.3 环境因子频率比分析
滑坡的发生是由多种内部因素和外部因素共同作用的结果[27–28]。参考江西省内其他与南康类似的研究区相关文献资料,考虑相关环境因子的客观实在性、统计继承性等原则,从数据源中获取地形地貌、基础地质、气象水文、地表覆被4个方面的19个环境因子数据用于易发性建模[29]。选择频率比(FR)模型处理滑坡与环境因子间的非线性响应关系来反映环境因子对滑坡易发性的影响程度[27]。当FR>1时,说明该因子所属区间有利于滑坡孕育;当FR<1,则说明不利于滑坡孕育。利用ArcGIS 10.2的自然断点法,将连续型的环境因子划分为8个子区间见表1[8],具体分布如图3所示。
2.3.1地形地貌因子
基于DEM利用ArcGIS 10.2获取其他地形地貌因子。由表1和图3(a)、(b)可知,高程在163.4~360.9m、坡度在6.2°~21.2°内,FR>1,表明中等程度海拔和坡度的区域是南康区滑坡的主要发生地。剖面曲率和平面曲率分别体现垂直方向、水平方向的地形复杂程度[23]。当剖面曲率介于1.3~10.4、平面曲率小于28.7时,FR>1,易造成滑坡的发生。地形起伏度从宏观角度反映研究区的地貌特征,其在20.0~100.1m内滑坡发生的概率较大。
2.3.2基础地质因子
岩性通过直接影响基岩和堆积体的力学性质来干扰滑坡的孕育[16,26]。地质调查显示,研究区内主要出露有变质岩、碳酸盐岩、碎屑岩,其中变质岩和碎屑岩的FR均>1。滑坡密度表示一定范围内所包含的滑坡点数量[27],滑坡密度大的区域是滑坡的高易发区。斜坡形态包括凹形坡、直线形坡、复合形坡和凸形坡4类。由表1可知,研究区内凹形坡和复合形坡有利于滑坡的发育。土壤黏/砂粒含量与水的渗透、侵蚀联系密切[30]。当土壤表层结构中黏粒比砂粒含量更低,底层黏粒比砂粒含量更高时土壤中水分的渗透作用增强,加重了斜坡体重量,从而促进滑坡面的形成[31]。
2.3.3气象水文因子
边坡受降雨冲刷易发生软化,且雨水下渗会改变坡体内部的力学性质[32]。由表1可知,降雨量高的区域滑坡发生的概率也更高。采用沟壑密度和改进的归一化差异水体指数(MNDW I)因子反映水文环境对滑坡的影响。沟壑密度定义为单位面积内沟壑河道的长度之和[33]。沟壑越密集的区域,受降雨、水系的侵蚀作用更加严重,滑坡发生的概率更高。MNDWI则能有效突显影像中的水体信息,揭示水体微细特征。
2.3.4地表覆被因子
归一化建筑指数(NDBI)能有效表示出研究区内建筑用地的信息,当NDBI在0.56~0.75范围内时有利于滑坡发生[25]。归一化植被指数(NDVI)反映区域内植被生长情况和覆盖程度,覆盖度高的区域通常滑坡发生的可能性较小[21]。总辐射包括水平地表所接受太阳的直接辐射与漫射辐射,通过影响植被生长和土壤湿度间接作用于滑坡的发生[8]。人口密度和GDP密度分别表示单位面积内人口数量和经济的分布特征。公路密度体现了研究区内公路修建的密集程度,道路修建过程中的开挖切坡行为会改变坡体的自然结构,破坏边坡坡脚的稳定从而促进滑坡的发生[16]。
3 不同非滑坡选择下的易发性结果
全区随机选择的方式从无滑坡区内随机选择与滑坡样本等量的2 598个非滑坡样本。根据南康区历史滑坡的地理特征和相关文献[16–17],认为坡度小于5°的属性区发生滑坡的概率较小,故筛选研究区坡度低于5°的栅格从中选择2 598个单元作为非滑坡。从缓冲区外选择时基于2 233个历史滑坡面创建距离大小为300m的滑坡缓冲区,在该范围以外随机选择2 598个非滑坡样本。
信息量法加权处理环境因子信息量值后,得到总信息量值的范围为–21.15~8.83。分区后在极低、低易发区中随机选择2 598个栅格单元作为非滑坡样本。
采用半监督法选择时从随机RF模型易发性分区的极低、低易发区中随机选择2 598个栅格作为可靠性更高的非滑坡样本。另外在进行样本非对称分析时,为构建滑坡与非滑坡比例为1∶2的样本集,将非滑坡样本个数增加至5 196个栅格。

表1 部分基础环境因子 F R 值Tab.1 Frequency ratios of some environmental factors
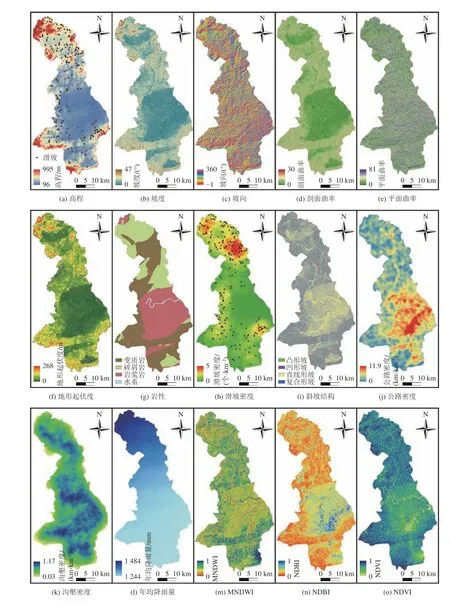
图3 滑坡基础环境因子Fig. 3 Basic environmental factors of landslide
3.1 RF的易发性建模
整个研究区采用30m的分辨率划分为2 0 6 3 002个栅格单元,将所有环境因子频率比分析后重新赋值的结果作为RF模型的输入变量。利用ArcGIS 10.2转换得到的2 598个滑坡栅格单元易发性并将其赋值为1,各方式选择的非滑坡样本易发性赋值为0,二者共同组成预测模型的输出变量[8]。联接滑坡与非滑坡样本及环境因子的FR值后合并构成等比例样本集作为训练/测试集,按7∶3随机划分为两部分,其中70%用于模型训练,30%用于模型测试[21]。
利用Python 3.8.8的Pandas、NumPy、Scipy等库对数据进行读取、计算和预处理,以及Scikit–learn库实现RF模型的机器学习过程[34]。由于构建RF模型时决策树的数量将对模型的整体精度造成影响,根据重复实验验证得最优的RF决策树数目并在模型中应用该参数进行预测[20]。
3.2 滑坡易发性预测结果
基于5种选择方式得到的非滑坡样本,利用Python 3.8.8对整个南康区栅格单元进行易发性预测,将易发性指数导入A rcGIS 10.2中制图。为方便对比不同选择方式的预测结果,结合易发性指数分布规律和自然间断点法将预测的易发性指数均按10%、10%、20%、30%和30%的比例划分为极低、低、中等、高和极高5个级别[12]。不同非滑坡样本选择方式的建模结果如图4和表2。
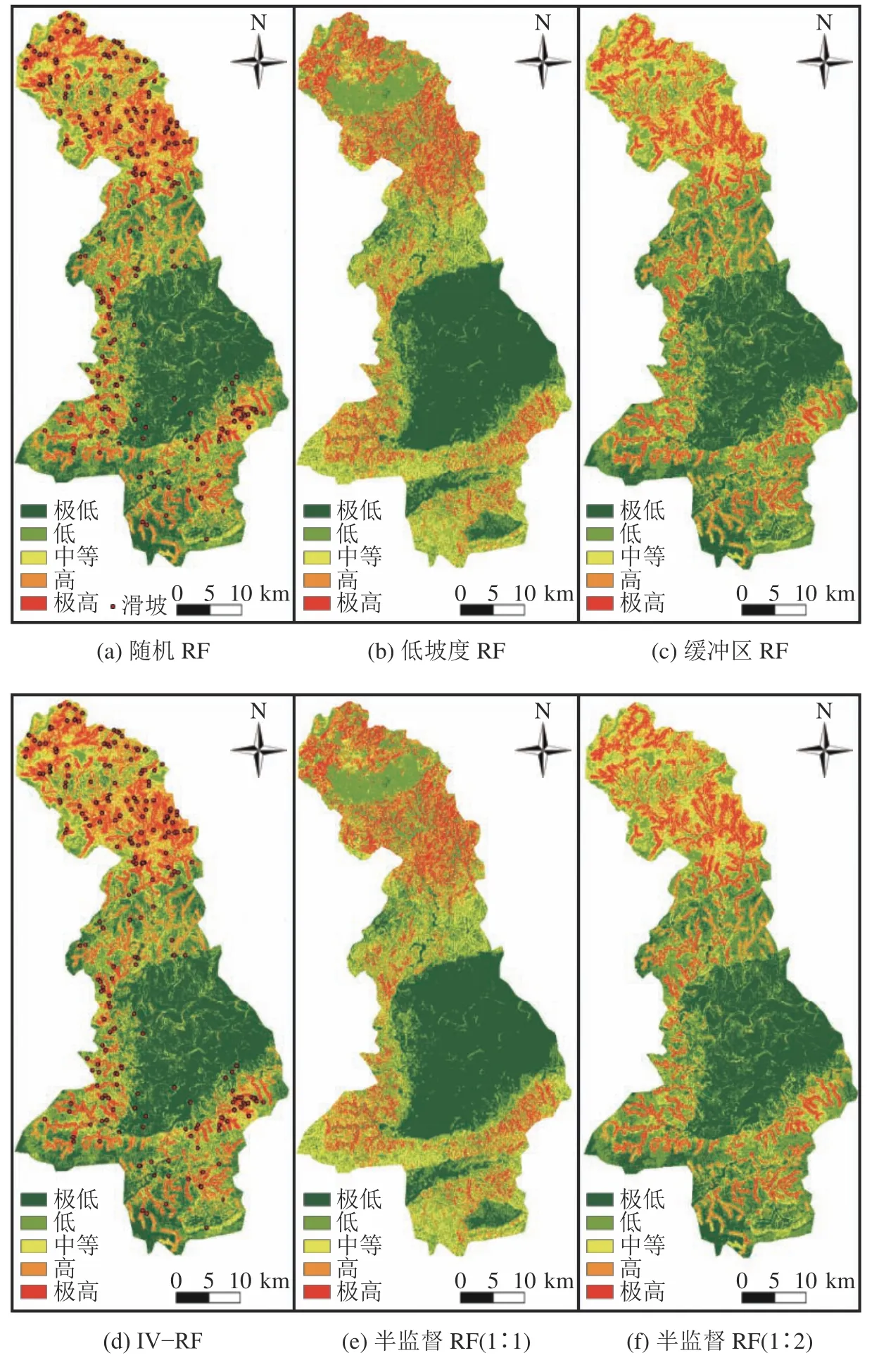
图4 基于不同非滑坡样本选取方法的滑坡易发性Fig. 4 Landslide susceptibility maps under different non–landslide selection methods
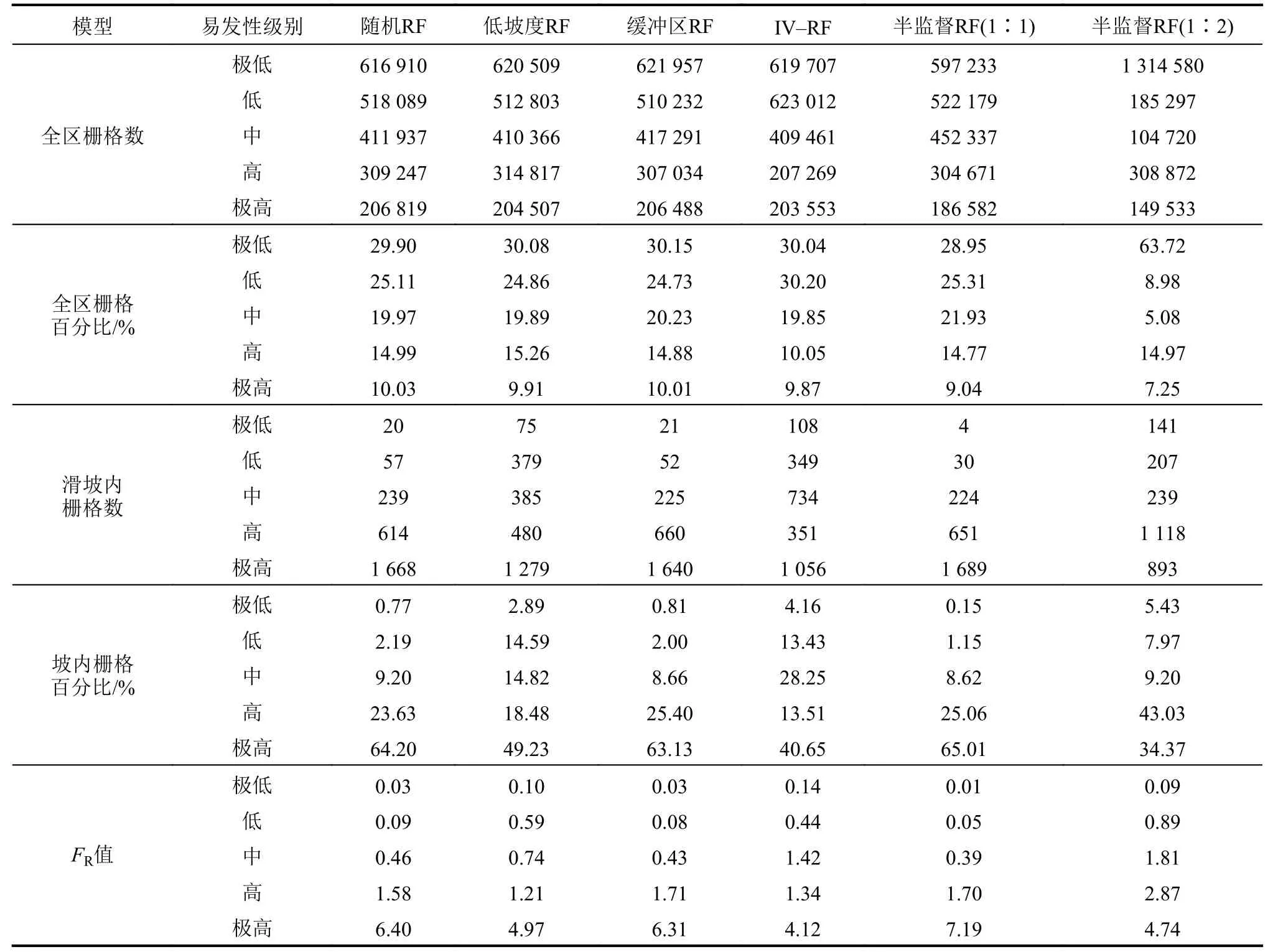
表2 基于5种非滑坡样本选择方式的易发性评价等级的统计结果Tab.2 Statistical results of susceptibility classification based on five non–landslide sample selection methods
由图4和表2可知,随着滑坡易发性级别的提高,其对应的FR值也逐渐增大,各方式预测的极高和高易发区内均包含了大部分的滑坡栅格单元。由此可见,5种选择方式预测的易发性图整体上相似,但对比细节发现预测结果间仍存在差异。使用等比例样本集(滑坡∶非滑坡=1∶1)的情况下,随机RF、低坡度RF、缓冲区RF、IV–RF和半监督RF模型中极高和高易发区的历史滑坡占比分别为87.83%、67.71%、88.53%、54.16%和90.07%。其中,半监督RF预测的极高和高易发区中包含的历史滑坡数量最多,表明半监督RF的易发性结果与已知滑坡的分布特征更加吻合,具有更优的建模性能。
4 滑坡易发性预测结果不确定性分析
4.1 模型精度评价
4.1.1 ROC精度评价
上述6种模型的ROC曲线及SAUC如图5所示。由图5可见:随机RF和缓冲区RF模型的ROC曲线相近且凸出程度较低,SAUC分别为0.895、0.896;低坡度RF模型SAUC高达0.973,可见,在坡度<5°的区域内,选择非滑坡样本显著提升了模型精度;半监督RF和IV–RF模型的ROC曲线均高于上述3种方式的ROC曲线,其中IV–RF的 SAUC为0.990,滑坡与非滑坡的比例分别为1∶1和1∶2时,半监督RF的 SAUC高达0.997和0.999,可见半监督RF模型的性能更佳,同时其在滑坡:非滑坡=1∶2的比例条件下预测精度最高。
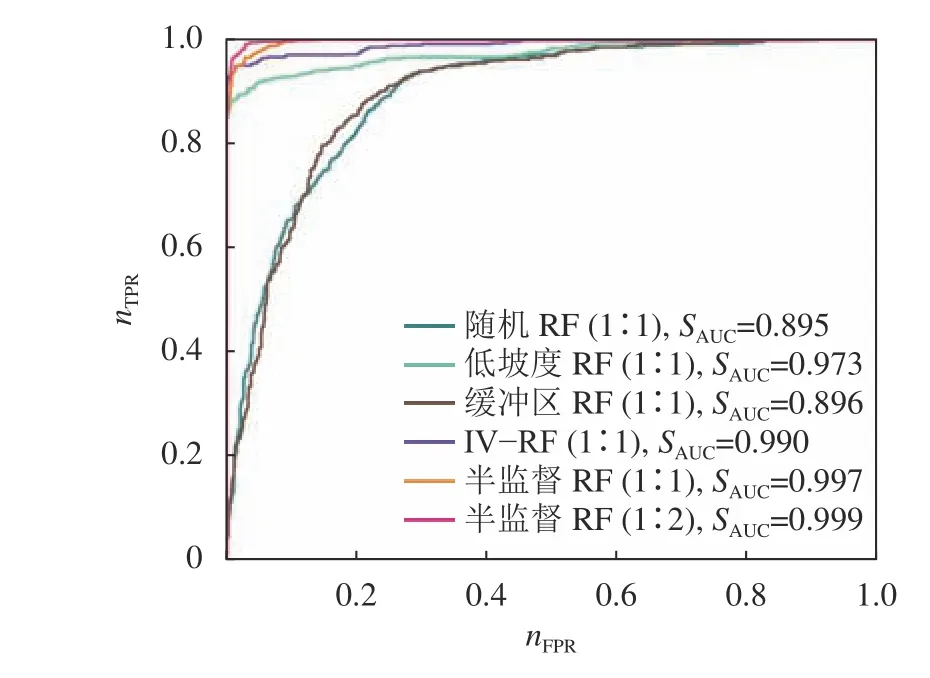
图5 不同非滑坡样本选择方式模型的ROC曲线Fig.5 ROC curves of different non–landslide sample selection models
4.1.2精度统计指标
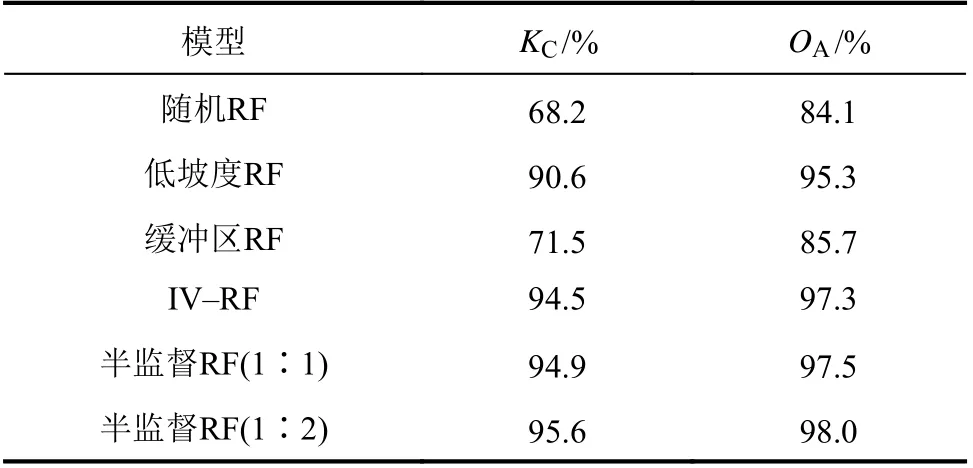
各耦合模型的精度统计指标如表3所示。由表3可知:KC和OA的大小排序均为随机RF<缓冲区RF<低坡度RF 将易发性指数在[0,1]范围内均分为100个区间进行统计分析,如图6所示。由图6可见,均值越小且标准差越大,说明建模过程中存在的不确定性越小。 表3 不同耦合模型验证指标Tab.3 Validation indicators of coupled different models 图6 不同非滑坡样本选择方式对应的易发性指数分布Fig. 6 Susceptibility indexes distribution of different non–landslide sample selection methods 1)随机RF与缓冲区RF模型的易发性指数分布规律较一致,整体上呈现随易发性指数增大而分布逐渐减小的趋势,且在极低易发区内均出现一段小幅增加。低坡度RF、IV–RF和半监督RF模型(滑坡∶非滑坡=1∶1)的易发性指数分布表现为低易发区和高易发区的分布较集中,而中间易发区分布较少。 2)各耦合模型的易发性指数按均值大小排序为:均值(IV–RF)>均值(低坡度)>均值(半监督1∶1)>均值(缓冲区)>均值(随机)>均值(半监督1∶2)。按标准差大小排序为:标准差(IV–RF)>标准差(低坡度)>标准差(半监督1∶1)>标准差(半监督1∶2)>标准差(缓冲区)>标准差(随机)。滑坡∶非滑坡=1∶1时各耦合RF模型的均值普遍较大。其中,随机RF和缓冲区RF的均值较小,分别为0.318和0.321;但二者的标准差也较小,分别为0.209和0.215,说明利用这两种方法进行预测时对易发性的区分度不高。低坡度RF和IV–RF的均值为0.518和0.625,标准差分别为0.351和0.371,相对于其他非滑坡选择方式,其均值和标准差均较大。半监督RF的均值为0.438,小于低坡度RF和IV–RF;且标准差为0.314,大于随机RF和缓冲区RF,综合而言半监督RF模型的预测性能更优。在滑坡∶非滑坡=1∶2时,半监督RF模型的均值为0.202,在6种模型中其均值最小,且易发性指数大部分位于极低和低易发区内,说明利用少量的高易发性指数能反映出尽量多的历史滑坡编录信息[8]。 环境因子的重要性是评估各因子对滑坡发生的影响程度的指标之一。将基础环境因子中具有较高重要性的因子称为滑坡易发性主控因子。在滑坡易发性预测过程中分析基础环境因子的重要性程度对易发性研究起到参考作用。本文利用Python 3.8.8对6种耦合模型中的19种环境因子进行分析,获得相应的重要性后,通过origin 2018软件处理得到各基础环境因子的重要性排序,如图7所示。 图7 不同非滑坡样本选择方式对应的环境因子重要性排名Fig. 7 Environmental factor importance ranking of different non–landslide sample selection methods 综合对比图7(a)~(f)可知,各耦合模型的环境因子重要性程度大同小异。随机RF和缓冲区RF中的环境因子重要性排序大致相同,两种模型中距离水系距离、坡度和滑坡密度等因子的重要性程度均较大。低坡度RF和IV–RF在因子重要性方面表现相似,坡度、地形起伏度、高程、岩性和滑坡密度等因子的重要性程度较大。而低坡度RF模型中坡度因子重要性占比更大,间接反映了非滑坡样本根据坡度特征进行选择。半监督RF模型中坡度因子对模型的影响程度最为显著,其次是距离水系距离、坡度、滑坡密度和年均降雨量等因子。 总体而言,坡度是南康区滑坡发生最重要的主控因子之一,在所有耦合模型中其因子重要性均较大。而MNDW I、NDBI和NDVI等环境因子对南康区滑坡事件发生的影响较小。结合南康区的滑坡成因以及地理环境条件可知半监督RF模型计算的环境因子重要性更加契合实际,可信度更高。 上述5种不同的非滑坡样本选择方式预测的滑坡易发性结果整体上类似。由于研究区内中等程度高程与坡度的地形地貌有利于边坡堆积层的形成从而促进滑坡发育,由表1可知,中等程度高程和坡度地区的FR均大于1。结合图3(a)~(b)和图4观察发现,滑坡的极高和高易发区常分布于此类地区。降雨量丰富且沟壑密度大的区域内,地表/地下水的渗流现象明显,滑带湿润情况严重会导致抗滑力显著下降[22],年均降雨量超过1322.9mm、沟壑密度在0.2~0.8的区域包含较多的极高和高易发区。当地的碎屑岩及变质岩原本的结构应力平衡易被破坏使坡体的力学强度下降[8],碎屑岩和变质岩对应的频率比分别为1.18和1.41,对比图3(g)和图4可知,这两种地层岩性区域滑坡易发性较高。观察NDVI环境因子可知,上述区域通常植被覆盖程度不高,间接加速了岩体的风化作用。南康区的滑坡极低和低易发区普遍海拔较高,且降雨作用不明显,水流下渗对斜坡体形成的影响较小,同时植被覆盖程度较高,有效降低了滑坡发生概率[21]。 随机RF模型选择非滑坡样本减少人为的干扰,其预测精度整体效果尚可且操作简便,故目前大多数研究采用随机方式选择非滑坡[15]。但由于该方法未考虑到无历史滑坡区域存在高易发性样本的可能,将影响非滑坡样本的质量和可靠性[35]。 从低坡度属性区选择非滑坡样本一定程度上提高了建模精度,目前已有部分研究应用此方式开展,例如Kavzoglu等[7]选择在坡度小于5°的地区进行采样。利用此方法时需要结合研究区地形确定合适的坡度范围以得到更可靠的非滑坡样本。对比图3(b)和图4发现,该模型预测结果中低坡度区内易发性指数均较低,而其他区域的易发性指数普遍较大,表明利用此方法选取得到的非滑坡样本进行预测一定程度的降低了模型地泛化能力,难以合理识别全区滑坡易发性。实际情况中低坡度地区与低易发区不能完全划等号,可见在低坡度区内选择非滑坡样本存在显而易见的缺陷[36]。 缓冲区RF模型能降低非滑坡样本的错误率,本研究对比不同缓冲距离的预测结果后,选择以300m作为缓冲距离展开研究。研究中最佳缓冲距离的确定与所选研究区的环境特征、数据源等有关,需要反复实验才能更好地确定[18]。不同研究区之间对缓冲距离的选择可能存在较大差异,如鲍帅[13]、Lucchese[18]等选择以1 km作为缓冲距离,而缪亚敏等[11]将200~500m范围作为最佳缓冲距离。然而由于人为局限了非滑坡样本的空间范围,易使非滑坡样本分布不够均衡。 针对上述非滑坡样本选择方式中存在的问题,现有研究中还存在基于自组织映射神经网络[12]、DBSCAN[13]的聚类分析法、目标空间外向化采样法[35]等均能获得更加可靠的非滑坡样本。本文进一步分析信息量法和半监督法以探索更高效准确地选择非滑坡样本。构建IV–RF模型进行预测时对易发性结果的可识别性效果不佳。结合精度和易发性指数分布规律可知,半监督法相比于其他4种方式具有更高的预测精度且更强的易发性指数分布规律性。 事实上,研究各类模型均是基于RF算法,差别在于不同选择方式得到的非滑坡样本可靠程度不同,从而影响滑坡易发性预测建模过程中训练测试集的质量。半监督模型的优势在于减小了模型训练和测试过程中由于非滑坡样本的质量产生的误差。半监督机器学习根据初次易发性预测结果,从极低和低易发区进行更加准确的采样工作,一定程度上提高了训练测试集的质量,从而提高了模型预测的精度且降低了建模的不确定性。 虽然各种方式构建等比例的滑坡–非滑坡样本开展易发性建模的预测精度均较高,但图6(a)~(e)显示其普遍存在易发性指数均值较大等问题。为进一步避免滑坡易发性指数分布不合理等问题,考虑采用不同的滑坡/非滑坡比例以尝试解决该问题。由于滑坡区域占少数,而非滑坡区域占多数,通过扩大非滑坡比例使模型更贴近研究区内真实的滑坡与非滑坡的数量关系[37]。对比5种非滑坡选择方式可知,半监督法的效果最好,故本文利用更具代表性的半监督法构建滑坡∶非滑坡=1∶2的样本集进行易发性建模,并与等比例样本集下的半监督RF模型对比。 由图5可知,相较于等比例样本集,利用滑坡∶非滑坡=1∶2比例的样本集进行易发性建模的不确定性最低。其表现为1∶2比例下的结果中易发性指数主要分布在低和极低易发区且均值显著降低,使滑坡易发性指数分布更合理。当然,本文仅讨论了利用滑坡∶非滑坡=1∶2时构建半监督RF模型的情况,滑坡与非滑坡比例的问题有待研究,比如滑坡∶非滑坡=1∶3、1∶4、1∶5、1∶6等比例下的建模情况仍需进一步探索。 1)利用低坡度、缓冲区、信息量法、半监督法等方式选择非滑坡样本进行滑坡易发性预测建模时,构建的耦合RF模型具有比随机RF模型更高的预测精度。可见利用其他方式选择更可靠的非滑坡样本对提升易发性建模性能具有显著作用,准确的非滑坡样本有利于降低建模不确定性。 2)5种非滑坡选择方式耦合模型中半监督RF建模结果的精度高于IV–RF模型,其次是低坡度RF、缓冲区RF、随机RF模型。半监督RF模型结果中的均值和标准差分别为0.438和0.314,均值相对较小且标准差较大,其不确定性较小。半监督RF模型计算得到的滑坡环境因子重要性结果更贴合实际,半监督RF模型的滑坡易发性预测性能更优。 3)对比滑坡与非滑坡不同比例的工况显示,滑坡∶非滑坡=1∶2的半监督RF模型预测得到的滑坡易发性的均值显著减小到0.202,且获得的预测精度和Kappa系数最高,分别达到0.999和95.6%。由此可见,采用滑坡∶非滑坡=1∶2的比例建模能获得更准确可靠的滑坡易发性指数分布规律。4.2 不同非滑坡样本选择方式的易发性指数分布
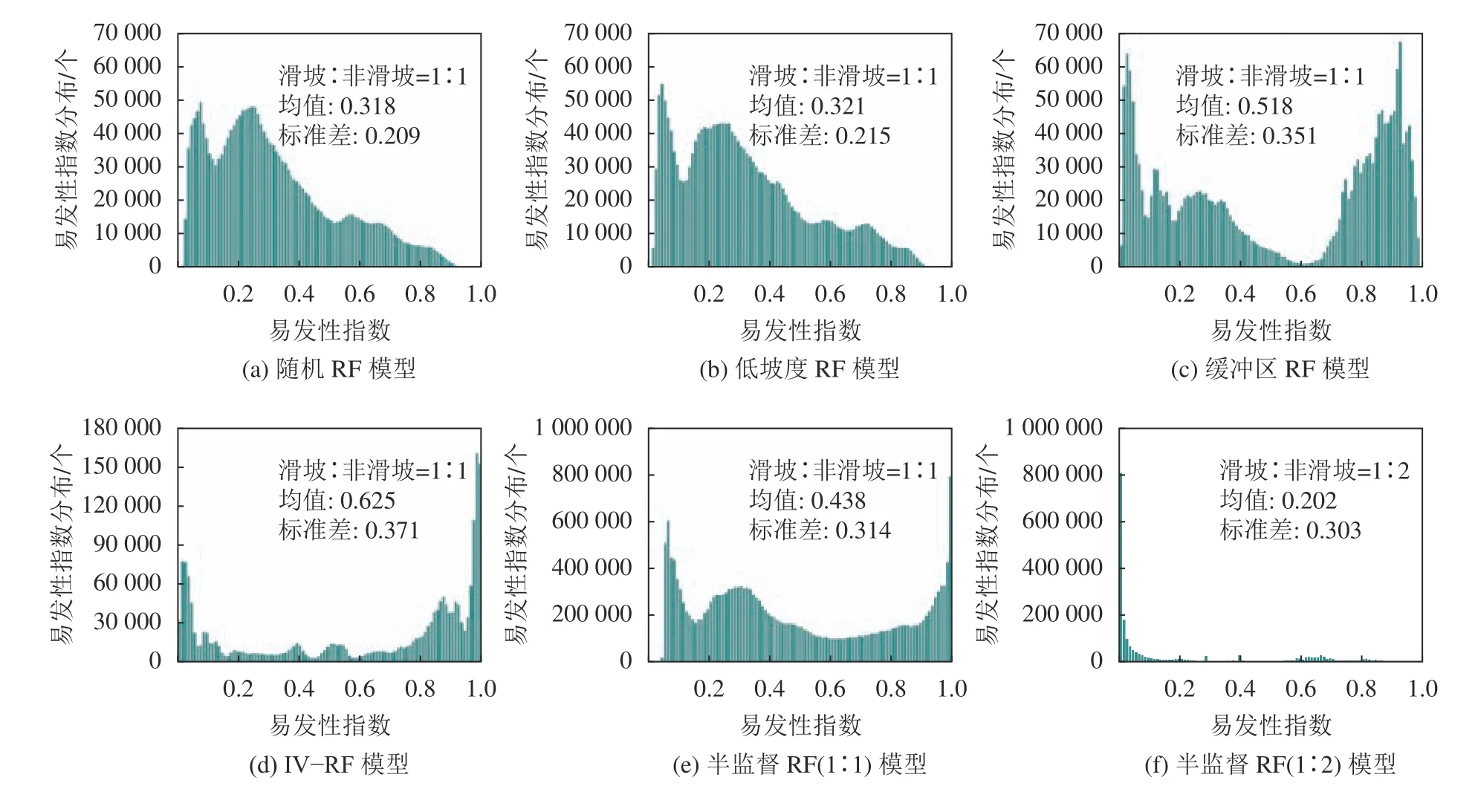
4.3 滑坡环境因子重要性分析
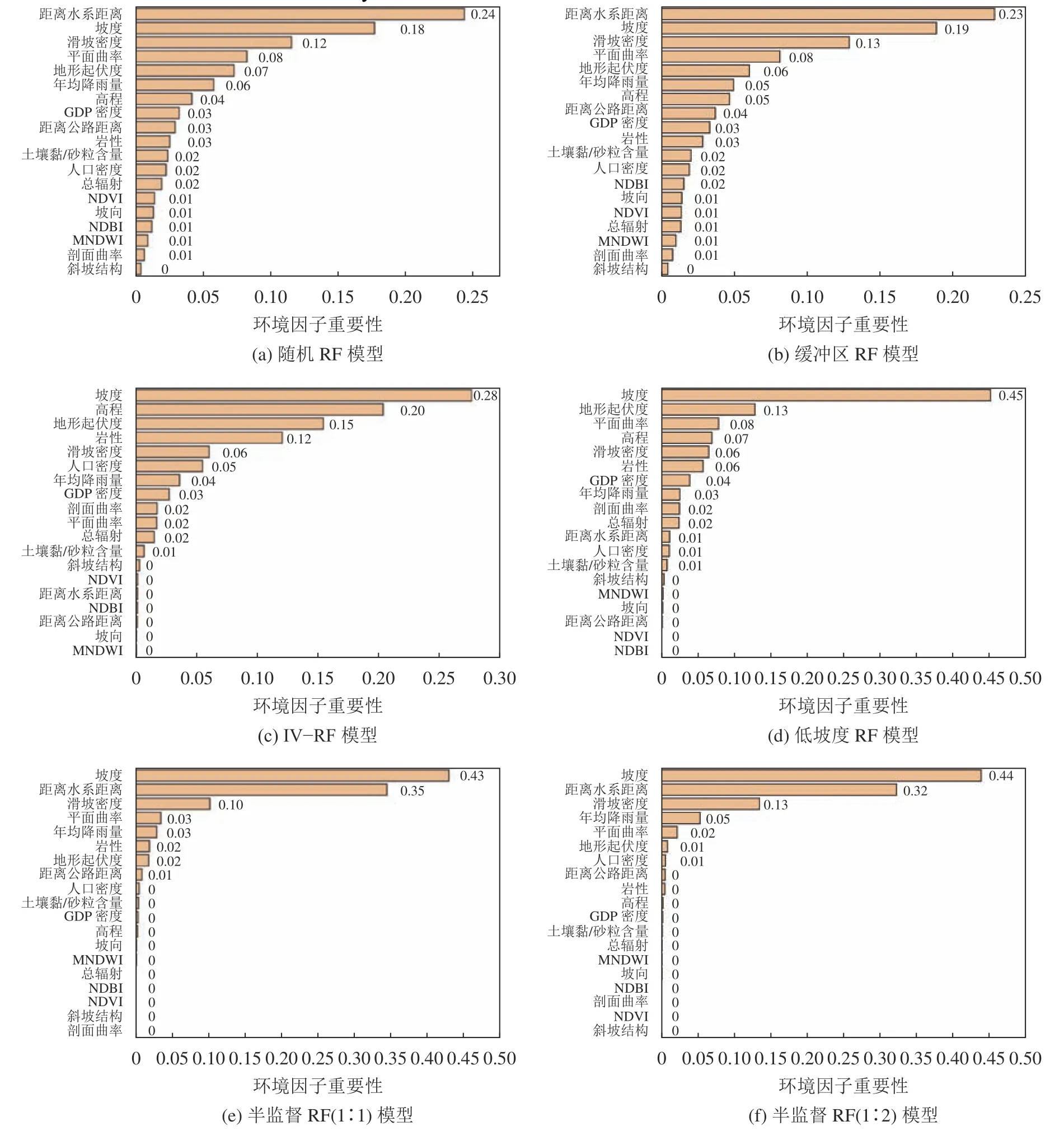
5 讨 论
5.1 滑坡易发性分区结果
5.2 不同非滑坡样本选择方式下的易发性建模
5.3 半监督机器学习中滑坡与非滑坡不同比例的预测建模
6 结 论
