渐进式滑坡锚索抗滑桩预应力张拉值计算

侯小强，王新飞*，贾洪璐，安玉科，周重任，侯云龙

(1.兰州交通大学土木工程学院，甘肃兰州 730070；2.中建路桥集团有限公司，河北石家庄 050000；3.甘肃省交通规划设计院有限公司，甘肃兰州 730030；4.甘肃省工程地质研究院，甘肃兰州 730030)

渐进式滑坡[1–2]的演化模式是一个动态发展的过程，且在一些规模较大的老滑坡中比较常见，如舟曲的立节滑坡[3]、秭归县谭家湾滑坡[4]等，其变形过程缓慢，受降雨和地震等因素影响呈现阶段性，完全失稳前一般存在较为明显的变形迹象，便于治理和避险。预应力锚索抗滑桩是近年来广泛应用于渐进式滑坡治理的支档结构形式[5]，其基本原理是在抗滑桩悬臂端设置一排或多排预应力锚索，使抗滑桩由原本的被动抗滑结构变为主动抗滑结构。由于锚索拉力的作用，可以有效改善抗滑桩工作时受力状态，优化桩身内力形式，提高抗滑能力，且能够大幅度减小桩长和桩身截面面积，从而降低工程造价，节省成本。随着铁路、公路以及水利水电工程中边坡和滑坡防治工程的日益增加[6]，研究渐进式滑坡锚索抗滑桩设计计算理论对解决此类工程问题意义重大。

目前，国内锚索抗滑桩预应力值研究主要体现在满载阶段开展锚索设计理论和桩锚协同设计计算两个方面。Jinoh[7]和Martin[8]等通过建立3维有限元模型，研究锚索桩–土耦合作用关系，结果表明桩土相对刚度对桩的破坏模式有重要影响。Ochang等[9]基于耦合欧拉–拉格朗日分析研究荷载倾斜角对不同类型螺旋锚的抗拔能力的影响，并提出一种归一化的载荷能力关系。Zhao等[10]优化了预应力锚索h型抗滑桩结构内力和位移计算方法，基于优化方法可以明显降低前后桩峰值弯矩和桩顶位移。曾德荣等[11]将锚索抗滑桩受荷段按结构静力问题计算，锚索拉力视为外荷载施加在受荷段，锚固段按W inkler弹性地基梁计算，此法可以简化锚索抗滑桩的计算过程。王化卿等[12]根据抗滑桩桩后作用的滑坡推力以及桩前滑面以上岩土体抗力，先行计算出滑面处剪力，将锚索拉力设计为滑面处剪力的1/2～4/7，所得锚索设计拉力即为锚索初始预应力。桂树强[13]根据桩锚变形协调原理，将锚索的预应力按锚索设计拉力的60%～80%考虑，建立其力学和数学模型，求得其锚索设计拉力，得到桩身内力分布的解析解，计算出的锚索拉力需根据桩顶位移控制条件进行反复校核，直到指标满足要求为止。金布格等[14]提出用控制桩顶水平位移的方法计算锚索设计拉力，将桩顶的最终位移控制作为设计标准。董建华等[15]研究地震作用下预应力锚索抗滑桩的工作机理和动力计算方法，建立了预应力锚索抗滑桩滑坡防治结构的动力计算模型进行地震响应分析。刘小丽等[16]以滑面处桩身弯矩为0为控制条件来计算锚索设计拉力，再根据桩–锚变形协调条件求得锚索预应力。王成汤等[17]开展了锚索抗滑桩加固堆积型滑坡的受力特性及其联合抗滑机制，通过室内试验和数值模拟对比分析锚索抗滑桩桩身变位、内力以及滑体深部水平位移的变化规律。

在桩锚协同设计计算方面，毛明章等[18]考虑桩锚之间协调变形作用，分析预应力锚索抗滑桩协同工作机理，将坡体内侧位移加入到方程中，建立桩锚协调变形计算模型。石海洋等[19]采用力法求解锚索抗滑桩的结构内力，并提出锚索与抗滑桩的荷载分担比初步可按照30%～40%进行设计。陈占[20]将抗滑桩受荷段采用挠曲变形理论，锚固段采用弹性地基梁理论，计算锚索抗滑桩桩锚变形协调下桩的变形与内力，通过控制滑面处变形和桩身内力形式来计算锚索初始预应力值和锚索自由段长度。王贵华等[21]基于桩–锚变形协调原理，构建了复合多层滑床条件下锚索抗滑桩计算分析模型，提出复合多层嵌固段抗滑桩内力和变形计算方法，结论表明：传统算法较为保守，改进算法可以减小桩顶位移及桩身内力。戴自航等[22]未考虑桩锚变形协调条件，将锚索拉力视为集中力作用于抗滑桩受荷段，利用有限差分法对锚索抗滑桩的桩身变形和内力进行了计算。周德培等[23]将抗滑桩受荷段视为超静定结构，考虑桩锚变形协调条件，按地基系数法确定锚索拉力及抗滑桩锚固段桩身内力。陈昌富等[24]基于加权残值法建立了考虑预应力损失的锚索抗滑桩内力与变形计算方法。上述锚索抗滑桩设计方法大多基于最大滑坡推力进行锚索拉力最终设计值的计算，对于施工阶段锚索初始张拉值设计方法研究较少，尤其是针对渐进式滑坡变形特点的锚索抗滑桩初始预应力设计理论尚无人研究。由于渐进式滑坡独特的变形特征，锚索抗滑桩的受力状态和工作机理在时空演化规律上与渐进式滑坡的动态蠕变过程具有一致性，因此，目前研究成果不适用于渐进式滑坡作用下锚索抗滑桩预应力值计算。

基于此，结合渐进式滑坡的变形特点和锚索抗滑桩的实际动态工作过程，考虑了锚索–抗滑桩–土体各阶段桩后土压力空载和满载两阶段对锚索抗滑桩工作机理的影响，构建了锚索抗滑桩不同阶段的计算模型，并优化桩锚变形协同条件，推导渐进式滑坡锚索抗滑桩初始预应力计算方法，结合具体算例进行验证该方法的合理性。

1 基本计算原理

渐进式滑坡的动态变形模式和锚索抗滑桩的动态工作过程是由“桩–锚–土”的协调变形共同完成的。抗滑桩在施工成桩后施加预应力张拉时，桩后滑坡推力尚未开始作用，坡体处于空载工作状态，随着坡体变形达到最大值时，滑坡推力全部作用于抗滑桩，此时锚索抗滑桩处于满载工作状态。为此根据锚索抗滑桩桩土相互作用工作过程，依据锚索抗滑桩内力和变形将其按照初始阶段到满载阶段开展锚索预应力初始设计拉力计算方法研究。

1.1 锚索预应力空载阶段

锚索抗滑桩的初始预应力阶段，其主要受锚索张拉产生的桩土相互作用，桩后岩土体产生一定的被动挤压，其土压力状态与所张拉的初始锚索预应力数值大小有密切关系，当所施加的锚索预应力不断增大，桩后坡体将产生向上运动的趋势，使桩后土压力先后表现为主动土压力、静止土压力及被动土压力状态。

1.2 锚索预应力满载阶段

锚索抗滑桩承受全部滑坡推力作用，抗滑桩内力和变形达到最大，锚索拉力也达到最大值，此时锚索抗滑桩承受的荷载为满载阶段。现有预应力锚索抗滑桩锚索预应力设计计算理论研究较多[10–15]，本文在现有抗滑桩的研究资料基础之上，对文献[10]锚索设计拉力计算条件进行了优化，满载阶段抗滑桩桩身弯矩的分布形式是最能直接、准确反映抗滑桩受力状态以及变形形式的力学参数，从锚索抗滑桩全桩内力均衡分布形式出发分析满载阶段抗滑桩的受力状态和稳定性。

1.3 桩–锚协调变形条件

预应力锚索抗滑桩桩–锚协同变形即考虑锚索作用点处锚索的水平伸长量与桩身水平位移相协调。初始阶段受锚索初始张拉力作用，抗滑桩桩顶产生倾向于坡体内侧的位移；满载阶段滑坡推力完全作用于抗滑桩桩身之上，锚索产生张拉变形，抗滑桩产生向远离坡体一侧的桩顶位移。

图1为初始阶段桩身位移示意图。图1中，a0为初始阶段桩顶位移， θ为锚索与水平面夹角。由图1可见，初始阶段由于锚索预应力张拉作用，抗滑桩产生趋向坡体内部方向的桩身变形。

图1 初始阶段桩身位移示意图Fig.1 Schematic diagram of the pile body displacement in the initial stage

图2为满载阶段桩身位移示意图。由图2可见，满载阶段滑坡推力增加到最大值，抗滑桩处于满载阶段，桩顶位移达到最大值，桩顶位移远离坡体。图2中：a1为满载阶段下的桩顶最终位移； ∆为满载阶段下的锚索变形量。考虑到实际工程中锚索的长度较长，同时锚索受力过程中会产生弹性伸长量，且预应力锚索抗滑桩桩顶位移一般严格控制在桩长的0.5%以内，微小的桩顶位移相较于锚索长度和桩身高度不足以使夹角 θ产生较大变化，因此，满载阶段未考虑锚索与水平面夹角θ变化。此时，桩–锚协调变形方程应为：

预应力锚索抗滑桩的桩顶位移ai、锚索变形量∆的计算方法为：

式（1）～（4）中：ai为桩顶位移；X0、ϕ0分别为抗滑桩锚固段顶端处桩的位移和转角；h1为抗滑桩滑面以上受荷段长度； ∆q、∆T分别为滑坡推力q及锚索拉力T作用下桩顶的位移； δ为锚索的柔度系数，即单位力作用下锚索的弹性伸长量；A、T分别为锚索的设计拉力和初始预应力；l、d分别为锚索自由段长度和单束锚索直径；Eg为锚索的弹性模量；N为单孔锚索的束数。

图2 满载阶段桩身位移示意图Fig.2 Schematic diagram of pile body displacement in the full-load stage

2 初始阶段锚索预应力

初始阶段滑坡推力未产生作用，锚索初始张拉力作用抗滑桩，使得桩后产生土压力，根据库伦土压力理论计算出抗滑桩桩后主动土压力、静止土压力、被动土压力大小，利用抗滑桩受荷段侧应力与土压力互等原则，得出不同土压力类型下锚索初始张拉力数值，探究不同土压力设计原则下锚索抗滑桩桩身内力特点，为满载阶段计算锚索设计拉力提供合理的初始张拉值。

将锚索抗滑桩受荷段视为悬臂梁，利用结构力学理论计算初始阶段锚索抗滑桩受荷段内力及变形，如图3所示。

图3 初始阶段抗滑桩计算示意图Fig.3 Schematic diagram of anti-skid pile calculation in the initial stage

式（5）～（9）中：i为锚索根数，i=0,1,2,3,···,n；h1为抗滑桩受荷段高度；b为桩截面宽度；y为抗滑桩桩顶至计算点距离；Ti为 初始阶段第i根 锚索的初始张拉值；θi为第i根锚索与水平面夹角；li为第i根锚索距滑面距离；I为桩截面惯性矩；为桩截面静距；Ej为桩后土压力类型，分别为主动土压力、静止土压力、被动土压力。

利用结构力学力矩分配法，即可求出不同锚索的初始张拉值，在求出锚索预应力的情况下，可以结合锚固段地层条件，依据W inkler弹性地基梁理论[25]，假设地基为连续线弹性介质，根据地基的刚度特性，设想桩与地基之间通过均匀分布具有特定刚度的弹性支座连接，基于以上假定进行初始阶段锚索抗滑桩锚索段的内力及变形计算，得出不同桩后土压力类型下预应力锚索抗滑桩全桩剪力、弯矩、变位、转角。

3 满载阶段锚索设计拉力计算

3.1 满载阶段受荷段计算

满载阶段锚索抗滑桩受荷段承担的荷载主要有滑坡推力及锚索设计拉力Ai，滑坡推力采用3种不同分布形式[26]（三角形、矩形、梯形）。因为三角形和矩形均为梯形的一种特殊形式，因此本次采用梯形计算图示，如图4所示。

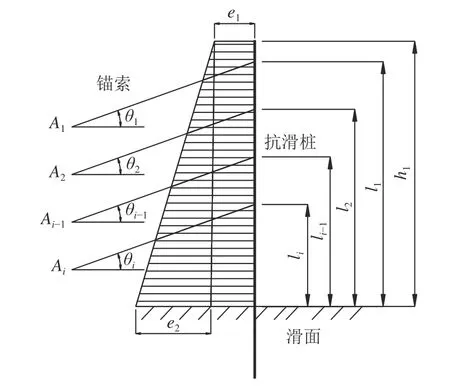
图4 满载阶段滑坡推力梯形作用抗滑桩计算示意图Fig. 4 Calculation diagram of anti-skid pile in full-load stage

利用结构力学力法和位移法可求受荷段内力及变位：

式（10）～（13）中，Ai为满载阶段第i根锚索的设计拉力，e1、e2为滑坡推力矩形分布时分量，E为弹性模量，其余同上。

3.2 满载阶段锚固段

满载阶段锚索抗滑桩内力设计基于全桩弯矩平衡设计原则，即：全桩正负弯矩面积相等原则。传统锚固段计算方法，采用查表的方式，计算步骤繁杂且误差较大，本文基于“m”法[27]解析解公式，利用MATLAB程序进行抗滑桩锚固段内力和变位计算，省去查表的繁琐步骤，同时提高计算精度，利用MATLAB积分函数对全桩弯矩积分，即可求出满载阶段正负弯矩面积相等时锚索设计拉力。

“m”法影响函数值A1-4、B1-4、C1-4、D1-4的计算方法：

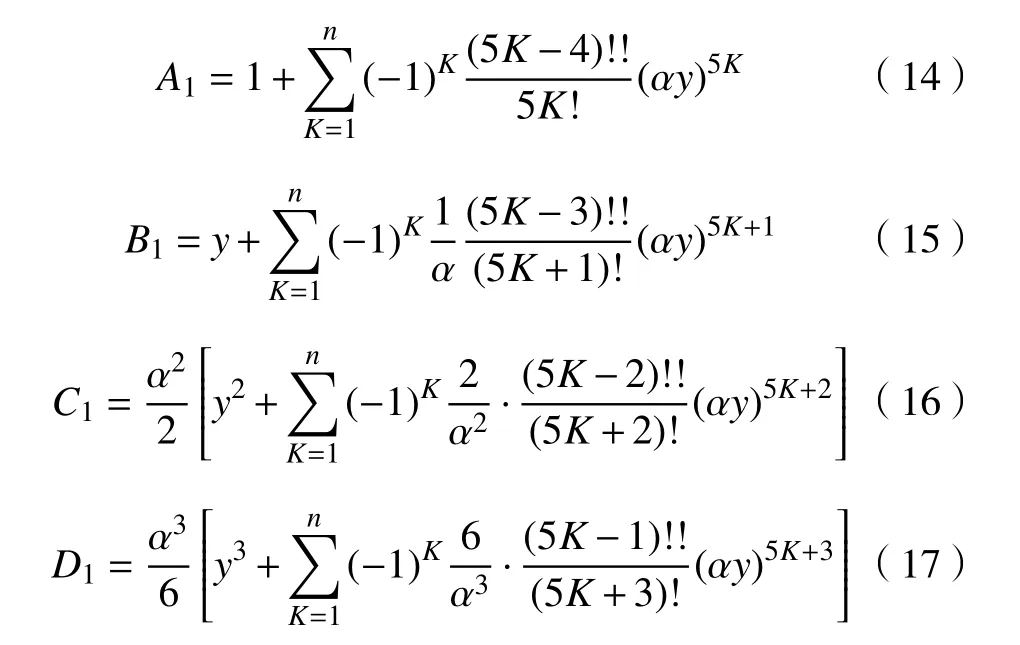
式（14）～（17）中， α为桩的变形系数，K取值为1,2,3,···,n。

其余影响函数值可分别由A1、B1、C1、D1对y微分得到：

因此，满载阶段抗滑桩锚固段内力变位计算矩阵可得：

全桩弯矩公式为：

令全桩正负弯矩面积相等，即对全桩弯矩积分，积分函数为零：

抗滑桩锚固段顶端弯矩M0和剪力Q0可由受荷段计算得到，锚固段转角 ϕ0和位移x0要根据桩底的边界条件（自由端、铰支端、固定端）来确定，对全桩弯矩积分求出满载阶段锚索设计拉力Ai后，将设计拉力Ai代入式（10）～（21），即可求得满载阶段锚索抗滑桩的剪力、弯矩、变位、转角。

3.3 施工阶段锚索预应力张拉值

根据满载阶段桩体最终位移，确定锚索抗滑桩的状态类型，结合初始阶段的桩身变位，利用桩锚协调条件，根据式（1）～（4）计算锚索预应力张拉值。桩锚协调变形条件下的锚索初始预应力张拉值：

桩锚协调变形下锚索预应力大小与初始预应力阶段计算得到的锚索预应力相接近，进行此步骤的计算可以对初始阶段锚索预应力进行验证，提高其准确和合理性。

4 算例分析

某滑坡经计算长期荷载作用的滑坡设计推力为Ep=1000kN·m–1，“桩–桩”中距为6m，抗滑桩上所受滑坡推力按梯形分布，水平分量分别为400 kN·m–1及800 kN·m–1，有限元模型如图5所示，滑坡推力分布如图6所示。滑坡体容重γ=19 kN·m–3，内摩擦角φ=26°，其治理措施采用了预应力锚索抗滑桩，桩顶位置设置一根锚索，锚索与水平面倾角为20°，抗滑桩采用C30混凝土浇筑，弹性模量Ew=3.0×107kN·m–2，桩截面为b×a=1.5m×2.0m，桩长为1 8m，滑面以上桩长为h1=10m，滑面以下桩长h 2=8m，滑动面以下的地基系数按“m”法计算，地基系数随深度变化的比例系数m=80000kN·m–4，桩底按自由端考虑。

图5 有限元模型Fig. 5 Finite element model

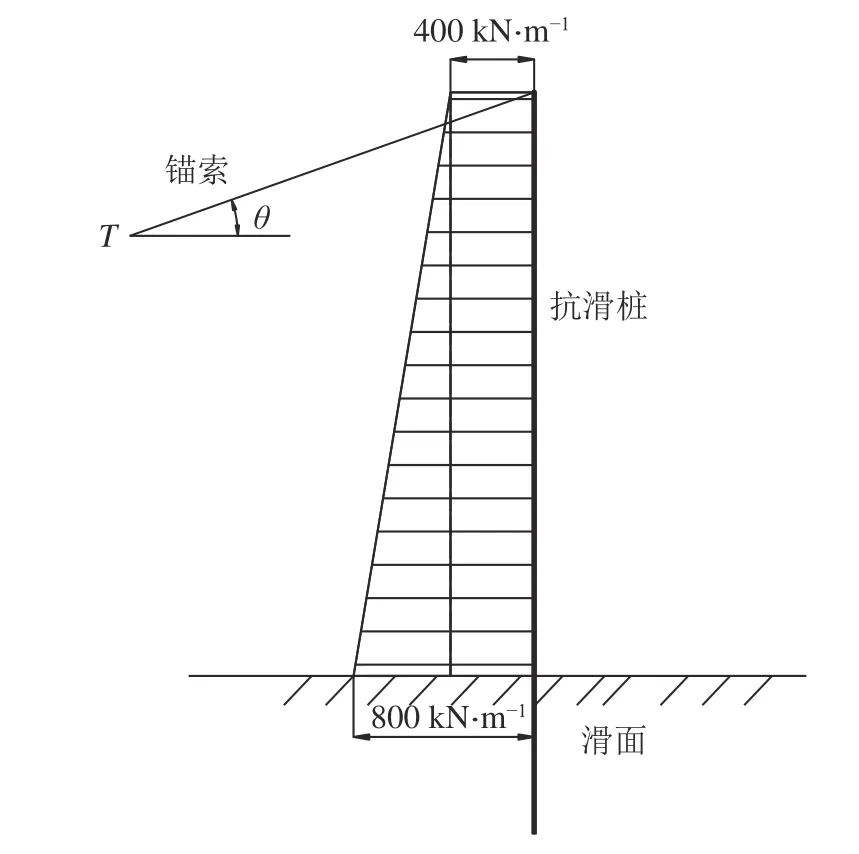
图6 滑坡推力作用示意图Fig. 6 Schematic diagram of landslide thrust action

锚索采用1860MPa、ɸ15.2mm高强度低松弛预应力钢绞线，单束截面面积140mm2，锚索自由段长度为13m，其弹性模量Eg=1.8×108kN·m-2，每孔按10束计。

1）抗滑桩的判定

依据《滑坡防治设计规范》（GB/T 38509—2020）抗滑桩变形系数计算要求，通过计算可得：

桩截面模量为：

抗滑桩基本参数见表1。

表1 抗滑桩参数Tab.1 Anti-skid pile parameters

桩的计算深度：αh2=0.384×8=3.07>2.5,因此，本设计资料下抗滑桩属于弹性抗滑桩[25]。

2）初始阶段锚索抗滑桩设计

根据式（7）～（10）可计算得初始预应力阶段桩后不同土压力类型时抗滑桩内力及变位，具体计算结果见表2，初始阶段桩身剪力、弯矩如图7所示。

表2 初始阶段抗滑桩内力变位Tab.2 Internal force shift of antiresistant pile in initial stage

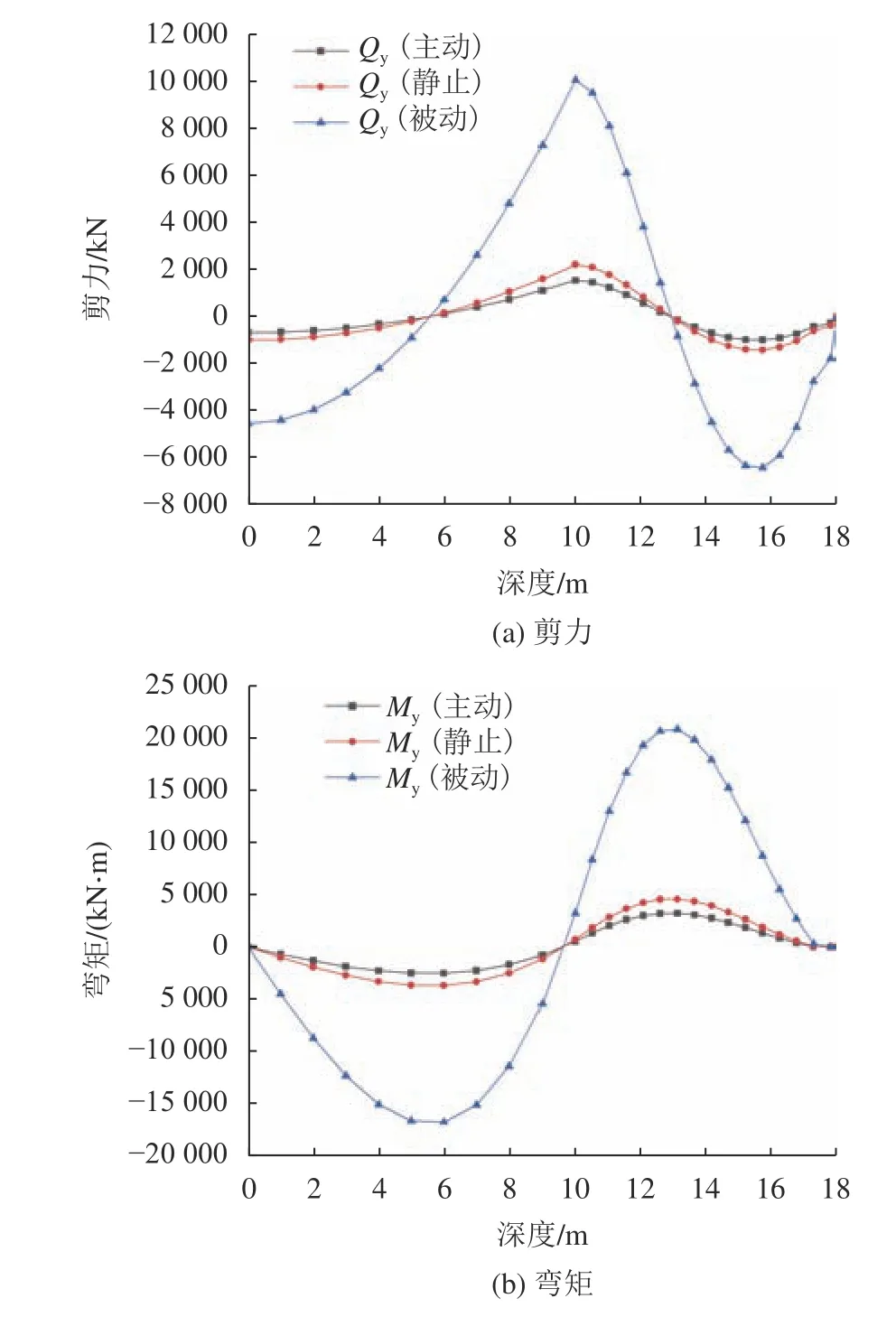
图7 初始锚索预应力阶段桩身剪力、弯矩对比Fig. 7 Comparison of pile shear and bending moment in the prestress stage of initial anchor cable

由图7可见：通过计算可得，初始锚索预应力阶段抗滑桩桩顶产生趋向于坡体内的位移，且抗滑桩桩顶位移满足《滑坡防治设计规范》（GB/T 38509—2020）要求的0.5%～1.0%；同时，不同的锚索预应力对应不同的桩后土压力状态，3种土压力临界状态时锚索抗滑桩内力可求。通过主动土压力、静止土压力以及被动土压力状态下锚索抗滑桩内力状态对比分析，确定满载阶段锚索抗滑桩锚索设计拉力的计算区间。由表2可知，静止土压力状态下抗滑桩初始预应力、滑面处剪力、弯矩极值以及桩顶位移等指标满足抗滑桩力学演化规律。由此表明，本锚索抗滑桩设计资料采用静止土压力状态作为设计标准进行锚索设计拉力计算。

3）满载阶段锚索抗滑桩设计

根据式（10）～（23），利用MATLAB程序可计算满载阶段锚索抗滑桩的内力和变位。选用现有4种不同计算方法与本文方法进行对比分析抗滑桩内力状态，同时利用ABAQUS有限元软件模拟满载工况，验证本文方法合理性。其中方法1[12]为设计拉力取滑面处剪力的1/2，方法2[12]为设计拉力取滑面取剪力的4/7，方法3[16]为使滑面处弯矩为0，方法4[13]的初始预应力是设计拉力的60%，具体计算结果见表3，满载阶段桩身剪力、弯矩如图8所示，桩身转角、位移如图9所示。

由图8、9和表3可知：方法1中满载阶段设计拉力最小，依次递增，方法4设计拉力最大；滑面处剪力均为正值，随着设计拉力的增大，滑面处剪力呈现减小的趋势；滑面处弯矩随着设计拉力的增大，同样呈现减小的趋势，但设计拉力达到一定值时滑面处弯矩变为0，甚至负值，此现象表明锚索拉力在抗滑桩满载工作阶段承担的贡献越来越大；桩身位移随着设计拉力的增加而减小，在受荷段减小幅度较为明显，在滑面以下2m之后减小幅度减慢，在滑面以下4 m之后桩身发生反方向微小位移，同时设计拉力越大，反向位移越小，表明在同样地层条件下，锚索设计拉力越大，反向位移越小，锚固力越小。

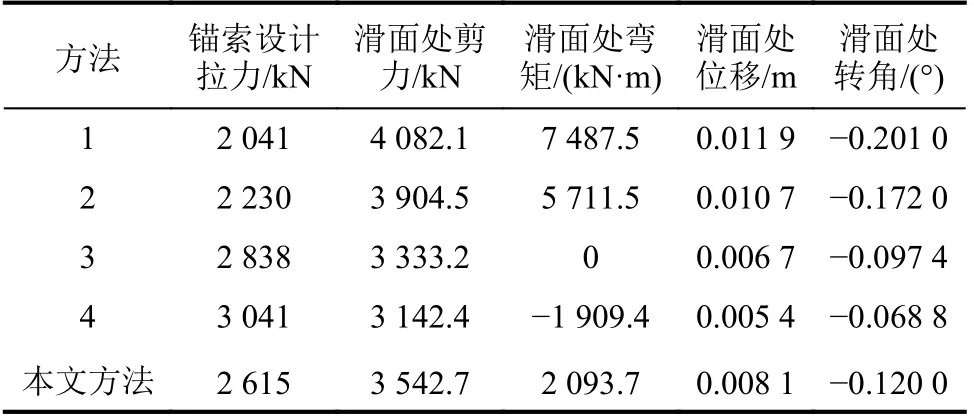
表3 不同设计拉力下抗滑桩桩身内力Tab.3 Internal force of anti-skid pile pile under different design tension

图8 满载锚索设计拉力阶段桩身剪力、弯矩对比Fig. 8 Comparison of shear force and bending moment of pile body in tensile stage of full load anchor cable design

由上述分析可知，为控制抗滑桩受荷段和锚固段弯矩平衡，将抗滑桩全桩弯矩正负面积之比作为一个新的比较参数，以此对比分析不同计算方法下抗滑桩的桩身受力情况。其中，方法1、方法2的桩身弯矩图正负面积之比分别为3.63、2.37，表明锚索设计拉力过小，导致受荷段弯矩过小，锚固段弯矩过大；本文方法中弯矩图正负弯矩面积之比为1，即其受荷段弯矩与锚固段弯矩分布基本一致，受力形式较为合理；方法3、方法4中弯矩图正负弯矩面积之比分别为0.55、0.30，表明锚索设计拉力过大，导致受荷段弯矩过大，锚固段弯矩过小；从全桩弯矩分布形式来看：方法1、2、3、4均属于受力不均的情况。

图9 满载锚索设计拉力阶段桩身转角、位移对比Fig. 9 Comparison of angle and displacement of pile body in tensile stage of full load anchor cable design

通过有限元模型模拟本算例满载工况下锚索抗滑桩的支护过程，提取桩身内力、变位等关键参数。由图8、9可知：其中数值模拟得到的桩身弯矩图正负面积之比为0.96，桩顶最大位移为4.32 cm，本文方法所得桩身弯矩图正负面积之比为1，桩顶最大位移为4.51 cm，数据证明两种方法得到的桩身内力形式基本一致，桩身变位在合理误差范围之内，能够一定程度验证本文设计方法的合理性和可靠性。

4）验证初始阶段锚索预应力

将所采用锚索的相关参数代入式（4）可得，本设计资料所选用锚索柔度δ=4.0×10–5m·kN–1，对本文方法下锚索设计拉力进行初始预应力校核。

将初始预应力阶段和满载设计拉力阶段相关数据代入式（24）可得锚索初始预应力为1 067.5 kN，初始预应力阶段桩后静止土压力状态下锚索初始预应力为1 059 kN，两者误差在0.79%，可以忽略不计，因此最终锚索初始预应力应为1 067.5 kN。

5）结果对比分析

满载设计阶段5种计算方法对比分析结果见表4。

表4 满载阶段不同计算方法对比分析Tab.4 Comparative analysis of different calculation methods in the full load stage

基于本文计算方法，预应力锚索抗滑桩具有理想的抗滑能力和锚固能力，桩身内力形式均衡合理，能够较好地发挥控制桩身变位的优势，预应力锚索起到良好锚拉加固的效果，同时不会造成锚索设计拉力的浪费，充分体现锚索抗滑桩力学机制的优点。

5 结 论

1）基于渐进式滑坡的徐变特点和锚索抗滑桩的实际工作演化过程，考虑锚索–抗滑桩–滑坡土体各阶段桩后土压力对锚索抗滑桩工作机理的影响，构建了初始空载和满载两阶段桩锚协同变形的计算模型，对比分析两个阶段的桩身位移和内力分布，直观反映渐进式滑坡支护中锚索抗滑桩的工作过程。

2）根据锚索抗滑桩动态工作过程，依据初始预应力阶段抗滑桩的受力变形特点，改进锚索抗滑桩的桩锚协调变形条件，同时考虑桩后土压力状态对锚索初始张拉力不可忽略的影响作用，避免预应力张拉值过小导致的桩顶位移、抗滑桩内力以及变形过大，预应力张拉值过大引起的桩身内力、变位过大和锚索预应力的浪费，为实现锚索预应力张拉值、桩身位移和内力介于两者之间，因此提出满载阶段全桩弯矩平衡的设计方法。

3）考虑多种工况条件下的锚索抗滑桩桩身变位形式，依据全桩弯矩平衡设计原则，通过算例对比分析不同计算方法，结合有限元数值模拟验证，结果表明：本文计算方法在桩身位移、变位控制以及桩身内力形式均优于其它算法，同时与数值模拟结果较为贴合，验证了弯矩平衡设计方法的合理性。但目前研究适用于均质地基条件下施工阶段锚索抗滑桩的设计计算，对于多层复合地基条件下施工阶段锚索抗滑桩预应力张拉值的计算准确和适用性有待进一步讨论。