高焓流动中的可压缩颗粒两相流并行求解器:数值方法及其验证

李青 余钊圣 刘朋欣 李婷婷 陈坚强 袁先旭,†

北京大学学报(自然科学版) 第60卷 第1期 2024年1月

Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 60, No. 1 (Jan. 2024)

10.13209/j.0479-8023.2023.022

国家自然科学基金(12272398)、中国博士后科学基金(2021MD703970)和国家重点研发计划(2019YFA0405200)资助

2022–12–12;

2023–01–29

高焓流动中的可压缩颗粒两相流并行求解器:数值方法及其验证

李青1,2余钊圣3刘朋欣1李婷婷4陈坚强1袁先旭1,†

1.空天飞行空气动力科学与技术全国重点实验室, 中国空气动力研究与发展中心, 绵阳 621000; 2.天目山实验室, 杭州 310000; 3.浙江大学航空航天学院, 杭州 310027; 4.西安交通大学化学工程与技术学院, 西安 710049; †通信作者, E-mail: yuanxianxu@cardc.cn

在极端力学环境下可压缩点力颗粒两相流理论方程的基础上, 提出一种基于动态链表数组的并行颗粒求解器, 使其与可压缩流体求解器耦合。与基于欧拉坐标系的携带流体相不同, 基于拉格朗日坐标系的求解器采用动态链表数组对弥散颗粒相进行内存分配, 可以解决因使用全局数组解决拉格朗日/欧拉坐标系转换带来的弥散颗粒群内存利用率低和计算效率低下问题。最后对多物理效应的可压缩颗粒两相流求解器进行验证, 并在马赫数渐进趋于零的情况下, 对两个不可压缩槽道颗粒湍流标模进行验证。

动态链表数组; 拉格朗日/欧拉坐标系转换; 可压缩点力颗粒两相流直接数值模拟求解器

有关颗粒两相流的系统研究可以追溯至航天火箭发动机燃烧室固体铝粉的燃烧问题[1]。随后, 由于化工流化床的工业需求推进, 空天和太空工程的工业需求使得可压缩颗粒两相流的相关研究得到迅速的发展。高速烧蚀飞行器、航空发动机、大推力火箭发动机和超燃冲压发动机都包含极端力学过程[2]: 特征温度为为(103)～(104)K, 特征速度∞为(103) m/s, 特征马赫数 Ma 为(10), 特征雷诺数 Re∞为(106), 飞行高度为(10)km 等。航空航天中的颗粒两相流体动力学包含燃烧[3]、固体颗粒或液滴碰撞产生电荷[4–5]、热辐射和热对流[6]以及冷热壁诱导的热泳力[7]等多个子物理过程。多物理场的各个子物理过程同时同场耦合, 使得航空航天设备的流体力学问题变得复杂。传统的单相可压缩流动的理论、计算和实验方法已经无法满足当前紧迫的工业需求。

1 研究背景

1.1 可压缩点力颗粒两相流理论方程

李青等[8]给出极端力学条件下, 考虑多物理效应的可压缩点力颗粒两相流直接数值模拟求解器的理论方程(point-particle direct numerical simulation, PP-DNS), 如式(1)～(4)所示。式(1)和(2)为多物理效应下颗粒动力学和热力学的控制方程, 式(3)和(4)为流体动力学和热力学的颗粒两相流双向耦合方程。其中, 假设颗粒为数学上无穷小的没有体积的点源, 其动力学和热力学过程可以通过不同物理过程的理论或半经验公式表示, 并进行线性叠加。

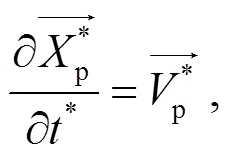
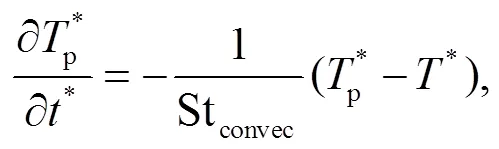
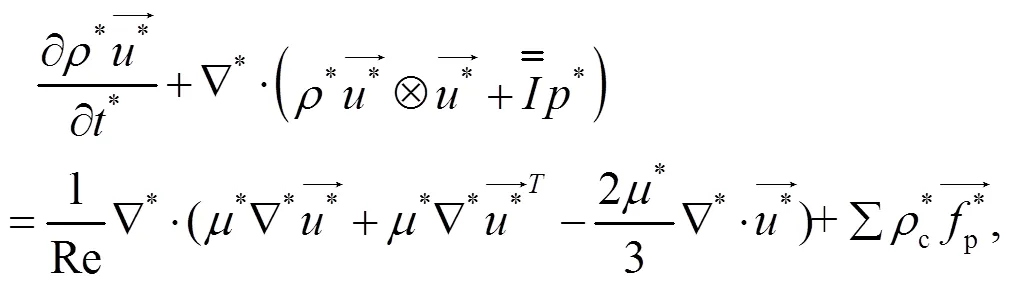
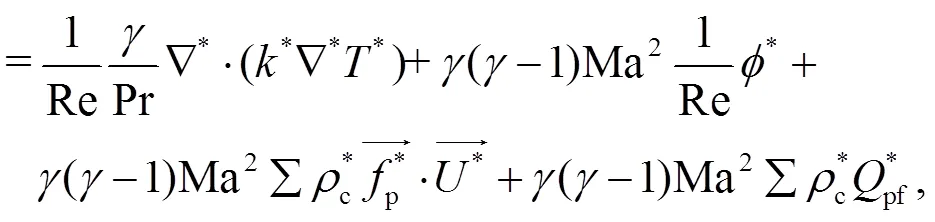
计算流体力学的核心是求解离散 Navier-Stokes偏微分方程组, 即离散相容方程组, 而不是 Navier-Stokes 方程本身, 因此 PP-DNS 数值求解器本质上是求解一个数值离散的偏微分方程组[9–10]来刻画流体力学过程, 并耦合求解一系列常微分方程组来刻画颗粒群的动力学和热力学过程。流体力学方程属于双曲守恒类偏微分方程[11–12], 如果数值离散带来的数值误差不能随时间衰减, 则会使得原本沿着特征线传播的信息不再满足双曲守恒律的影响域和依赖域关系, 最终导致数值求解器发散。颗粒动力学方程与流体力学方程的反馈耦合等效于在数值求解域的离散 Euler 点上增加了数值源项, 会增加流体力学的离散相容方程组的数值不稳定性和数值求解器的数值刚性, 使得满足数值稳定性条件的最大时间步更加苛刻。为了消除数值不稳定性, Pierce[13]采用 Runge-Kutta 三阶的多时间子步方式, 将弥散颗粒相的动力学和热力学信息分别反馈至可压缩流体力学的动量方程和能量方程。

严格地说, 求解颗粒两相流基本问题应该完全基于 Navier-Stokes 方程。以现有的不可压缩颗粒解析求解器[14]为例, 其采用比颗粒尺寸更小的数值离散网格, 获取有限体积颗粒周围所有的流体力学信息, 然后通过定义, 积分获得颗粒受力。这类方法采用 Lagrange 离散点或 Euler 离散点在颗粒体内或表面分布, 通过离散点反馈颗粒与携带流体的相间动量交换信息, 并通过积分获得有限体积的颗粒受力。这类方法属于全分辨颗粒直接数值模拟求解方法(particle-resolved direct numerical simulation, PR-DNS)。PR-DNS 的优点是不进行任何假设, 直接求解 Navier-Stokes 方程, 获得弥散颗粒与携带流体两相间的动力学信息(图 1)。缺点是需要比 PP-DNS 更小的数值离散网格, 会导致计算量陡增(图 2); 另一方面, 在相同颗粒数目的条件下, PR-DNS比 PP-DNS 带来更多的数值源项反馈, 从而带来比 PP-DNS 更强的数值不稳定性。真实工业问题的颗粒数目往往是十亿量级, 因此 PR-DNS 方法能且仅能用于简单标模研究[15–16]。李瑞元等[17]给出单个球形颗粒在可压缩均匀流中的直接数值模拟, 并验证了可压缩圆球扰流阻力表达式。值得一提的是, 当颗粒尺度比最小流动尺度小时, 流体对颗粒的作用力、颗流体对颗粒的作用力以及颗粒对流体的反馈可以近似地表示为点力模型[18–19], 即 PP-DNS 与PR-DNS 有着相似的精度。目前, 可压缩条件下的多颗粒 PR-DNS 研究尚罕有报道。

表示一般的颗粒相信息, 如颗粒受力Fp或温度Tp等

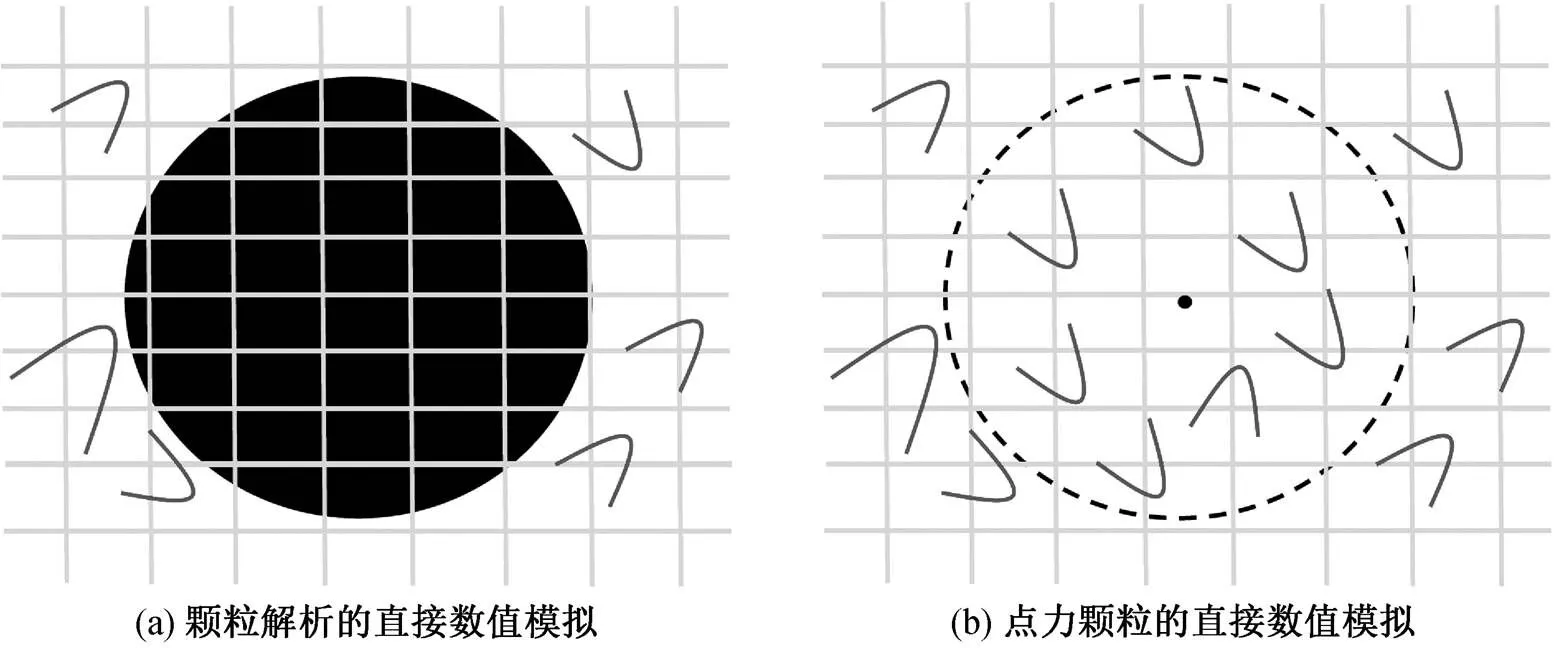
图2 颗粒解析直接数值模拟求解器与点力颗粒直接数值模拟求解器的对比

1.2 基于 PP-DNS 的颗粒湍流和颗粒两相流研究

采用 PP-DNS 作为直接数值模拟工具的颗粒两相湍流基础研究可分为两类: 一类是用 PP-DNS 方法进行颗粒湍流机理研究; 另一类是用 PP-DNS 提供直接数值模拟数据库, 用于构建工业软件模型, 如 PP-LES (point-particle large eddy simulation)。PP-LES 对携带流体相采用 LES 模型, 这类方法的核心问题是如何重构被粗网格忽略的亚格子脉动, 从而让弥散颗粒相能“感受”到原本被 LES 忽略的亚格子流体脉动, 复现弥散颗粒相的统计过程。LES-LES模型又称为 Euler-Euler 模型, 它是在 PP-LES 的基础上, 对弥散颗粒相进行连续性假设, 将弥散颗粒相的统计动力学过程模化为一个基于 Euler 坐标的偏微分方程组。连续性假设将弥散颗粒相的控制方程从一系列常微分方程组变成一个偏微分方程组, 大大减少了计算量。以 10 亿颗粒的工业流化床为例, 对 PP-DNS 而言, 弥散颗粒相至少需要求解 10亿组 6 个自由度变量的常微分方程组, 总共 60 亿个非定常变量; 同时需要考虑 10 亿个颗粒对携带流体相的插值反馈, 计算量巨大, 无法解决工业级别规模的真实航空航天问题[20–21]。对 LES-LES 而言, 基于 Euler 坐标的弥散颗粒相偏微分方程组的非定常变量不超过 10 个。因此, PP-LES和 Euler-Euler 模型往往被用于构建工业软件内核, 而两个模型的构建都需要 PP-DNS 提供参考颗粒湍流数据库。因此, PP-DNS 是开展颗粒两相流工业软件研发的直接数值模拟工具和重要手段。

Wang 等[22]和 Rosa 等[23]研究重力对各向同性均匀颗粒湍流的影响, 给出重力、颗粒惯性和湍流雷诺数三者之间的归一化表达式。Ferrante 等[24]研究微小气泡在壁湍流中的减阻机理, 发现弥散气泡相会调制减弱湍流雷诺应力, 并减小壁面摩阻。Lain 等[25]通过研究气固颗粒槽道湍流, 发现壁面粗糙度对湍流脉动统计量的影响不可忽略。Marchioli 等[26]发现湍流相干结构与颗粒涡泳现象密切相关, 并利用统计采样的颗粒湍流数据阐明湍流上扫和下掠过程与颗粒法向输运的关系。Mehrabadi 等[15]指出, 有限尺寸诱导的尾流效应只有在颗粒惯性大的时候才需要修正, 对于 St 为 1 量级的颗粒湍流, 采用 PP-DNS 就可以获得与 PR-DNS 近似的精度。Daitche[27]发现, 颗粒历史力效应会对颗粒的统计分布产生影响。Zamansky 等[28]发现, 受到太阳热辐射的黑体颗粒可以通过与携带流体相之间的相间传热, 改变颗粒湍流动力学过程。Zhao 等[29]推导了颗粒湍流能量平衡方程, 利用 PP-DNS 研究颗粒壁湍流的能量平衡, 阐明颗粒湍流相互作用的基本过程。在此基础上, Zhou 等[30]通过进一步的研究, 发现颗粒对壁湍流脉动应力的调制作用是非单调的。Pan 等[31]发现颗粒对湍流的做功过程是多尺度且各向异性的: 在平均尺度上, 颗粒在壁湍流外区吸收平均流场的动能, 且在近壁面为平均流场输入动能; 在脉动尺度上, 颗粒在流向上为湍流场输入动能, 在法向和展向上则从湍流场从吸收动能。Li 等[32]研究了惯性颗粒在不可压缩空间发展边界层中的动力学过程, 发现在其考察的参数范围内, 惯性颗粒会增加层流边界层和湍流边界层的摩阻。近年来, PP-DNS 在可压缩颗粒湍流的研究方兴未艾。Dai等[33]研究惯性颗粒在可压缩各向同性均匀湍流中的动力学, 发现颗粒减弱了可压缩性; 同时, 随着Stokes 数的变化, 惯性颗粒非单调地调制湍动能。Xiao 等[34]采用单向耦合方法, 研究低马赫数可压缩颗粒壁湍流中的颗粒运动和分布特性, 发现颗粒倾向性聚团机理与不可压情况类似, 与“上抛”、“下扫”和流动条带结构密切相关。

Wang 等[35]和 Fevrier 等[36]用 PP-DNS 研究各向同性均匀颗粒湍流, 在统计意义上给出颗粒脉动和湍流脉动的 Euler-Euler 预测模型。颗粒两相流工业软件 Neptune 的 Euler-Euler 就是基于 Fevrier 等[36]的工作开发的。随后, Yu 等[37]用 Neptune 数值预测化工管道中的磨蚀问题。Marchioli[38]指出, 由于 PP-LES 忽略了亚格子流体脉动, 使得颗粒的涡泳统计过程与 PP-DNS 有差异, 并且, 如何在 PP-LES 中重构被 LES 忽略的小尺度脉动, 并重新让颗粒“感受”到, 是构建 PP-LES 模型的关键。

2 数值方法

2.1 流体求解器

本文在极端力学环境下可压缩点力颗粒两相流理论方程的基础上, 开发一种可压缩流动条件下基于动态链表数组的 PP-DNS 求解器, 使其能够与可压缩流体求解器耦合。

Tian 等[39]开发了可压缩点力颗粒两相流直接数值模拟求解器并进行验证, 其基本理论方程考虑了颗粒相间阻力和相间阻力做功。本文开发的颗粒求解器在数值方法上与之类似, 并在其基础上考虑了多物理效应[3,8]。

本文采用任意阶 Lagrange 插值[40]来实现 Euler 坐标点到弥散相颗粒 Lagrange 点的插值转换, 如式(5)和(6)以及图 3(a)所示。

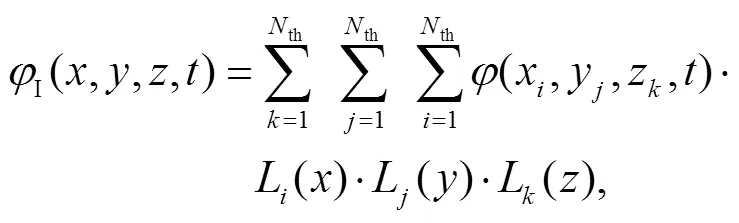
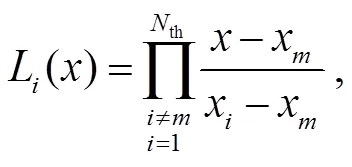
其中,I(,,,)一般地表示 3 个方向的速度分量(I(,,,),I(,,,)和I(,,,))、可压缩流体的密度I(,,,)、温度I(,,,)或动力黏度I(,,,),th表示某方向上的 Lagrange 插值阶数。

2.2 颗粒求解器

将颗粒动力学以及热力学方程写入流体求解器的 Runge Kutta 三阶时间步推进循环(式(1)和(2))中, 相间阻力、相间阻力做功以及热对流项对流体相的反馈采用与流体求解器 OpenCFD 同步的时间推进[9,41–42]:

红色点为Lagrange坐标点, 蓝色点为Euler坐标点

图3 从Euler坐标点到Lagrange坐标点(a)和从Lagrange坐标点到Euler坐标点(b)的插值示意图

Fig. 3 Illustration of interpolation from Euler point to Lagrange point (a) and from Lagrange point to Euler point (b)

红色部分是任意位置的MPI分块

其中,表示 Runge-Kutta 三阶时间步推进的子循环步, 先后取=1, 2, 3; conservation 项表示可压缩流体力学数值离散方程的守恒项; source 项表示颗粒相对流体相的反馈。

真实的航空航天可压缩颗粒两相流问题往往更复杂, 复杂的偏微分方程会导致其数值离散相容方程变得具有数值刚性。从数值稳定性的角度讲, 满足稳定性的最大时间步变得越来越小, 使得计算量剧增, 导致可以研究的参数范围受到极大的限制。针对此问题, Pierce[13]开发了时间分步推进结合压力泊松方程修正的数值算法, 得到广泛应用[43–44]。压力修正算法最早源于不可压缩单相流动的数值求解[45–46]。由于流体力学方程组本质上是一种双曲型和抛物型的偏微分方程组, 其不稳定性主要来源于双曲型偏微分方程的非线性惯性对流项[47]。数值稳定性的获得与高精度解析湍流小尺度脉动是一对矛盾体: 一方面, 如果引入过多的数值黏性获得稳定性, 会导致湍流高阶统计矩无法准确捕捉湍流特征[48]; 另一方面, 如果采用高精度算法, 数值刚性会导致最大稳定时间步太小, 使得计算没有效率[10,49–50]。本质上, 压力修正方法等效于引入质量守恒条件约束。压力修正算法的意义在于, 在数值精度和数值稳定性二者之间达到平衡。

2.3 弥散颗粒群在并行分块中的通信

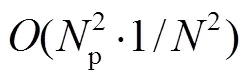
图 4 为颗粒求解器的 MPI 分块间的通信示意图。任意位置的 MPI 分块与其相邻的 26 个 MPI 分块依次发送或接收颗粒相信息, 从而依次修改或增删动态链表数组信息。动态链表数组结合MPI分块的通信技术, 提高了通信效率, 避免了 MPI 通信过程中的死锁。

3 标模验证算例

3.1 单颗粒问题

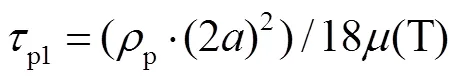
3.1.1插值精度和并行分块

表 2 给出流场参数设置, 式(8)给出惯性颗粒在Taylor-Green 涡中的控制方程, 采用单向耦合的 PP-DNS 与理论解对比。关闭 OpenCFD 的可压缩求解器, 全场定常施加一个不可压缩的 Taylor-Green 流动, 从而避免构造可压缩流场的繁琐。理论解如式(9)和(10)所示, 理论速度*采用 Taylor-Green 解析解, PP-DNS 使用的*从施加流场插值获得。图 6 表明, Lagrange 插值算法的精度误差随着阶数的增加而减小, 随着网格尺寸的减小而减小。

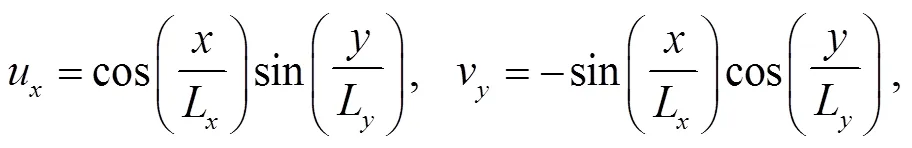
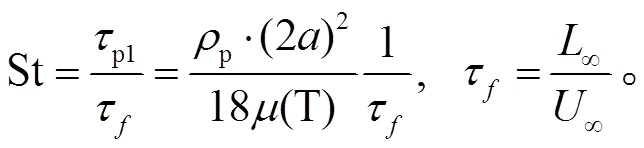
一个单向耦合惯性颗粒在 Taylor Green 涡中的运动如图 7 所示。可以看出, PP-DNS 求解器的动态链表数组通信模块调试成功, 颗粒可以在不同 MPI分块之间准确地收发通信, 不需要单独分配缓冲内存来交换弥散颗粒相的数据。

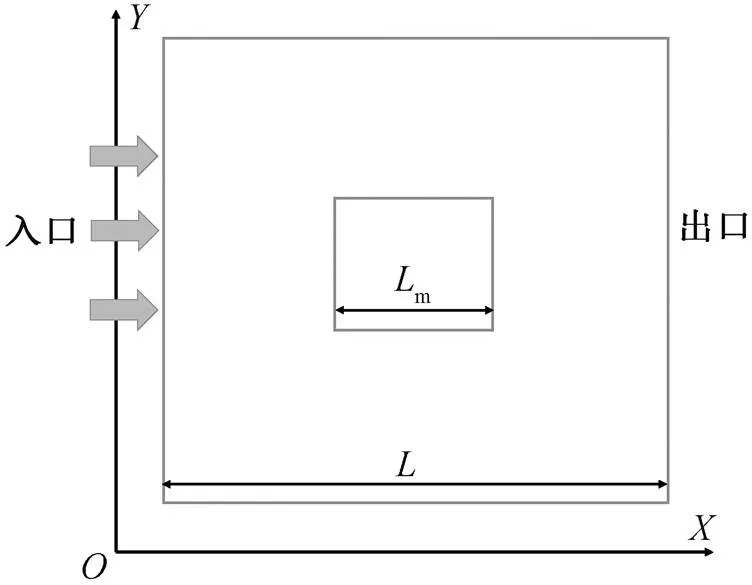
图5 可压缩均匀流的DNS数值网格示意图

表1 可压缩均匀流的DNS流场参数设置

表2 单向耦合施加的不可压缩Taylor-Green流场参数设置

图7 动态链表数组并行分块验证

3.1.2考虑可压缩效应的相间阻力

对于均匀流中的颗粒非定常速度问题采用双向耦合验证, DNS 设置见表 1, 来流速度为*=0.6。颗粒在可压缩流动中的统计定常阻力公式可以近似表示为滑移马赫数和滑移雷诺数的函数[51–52](式(11)), 理论解可以表示为式(12)[8]。图 8 表明, 本文的 PP-DNS 结果与半经验理论解(式(12))吻合。

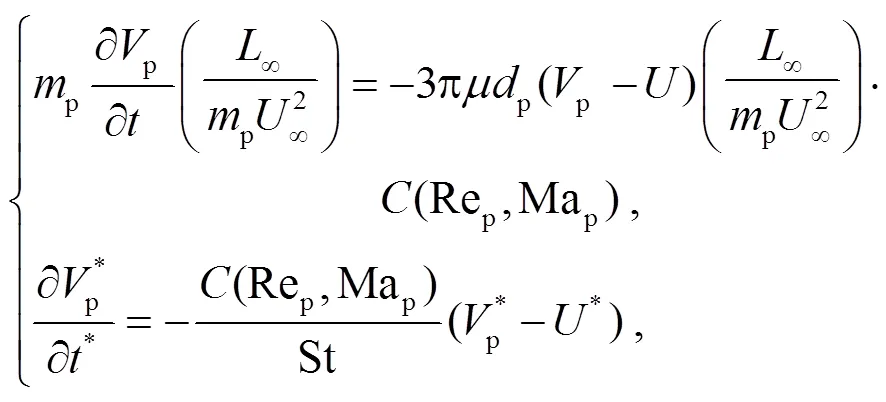
(12)

3.1.3 历史力

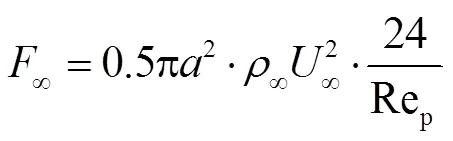
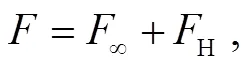
3.1.4 重力

重力作用往往在湍流脉动尺度上影响颗粒动力学[22–23], 有研究发现在槽道流中重力影响湍流统计矩[55–56]。式(14)为考虑 Stokes 阻力和一般重力场作用下的颗粒动力学方程, 式(15)为理论解[8]。图 10表明, 本文 PP-DNS 结果与半经验理论解(式(15))相吻合。

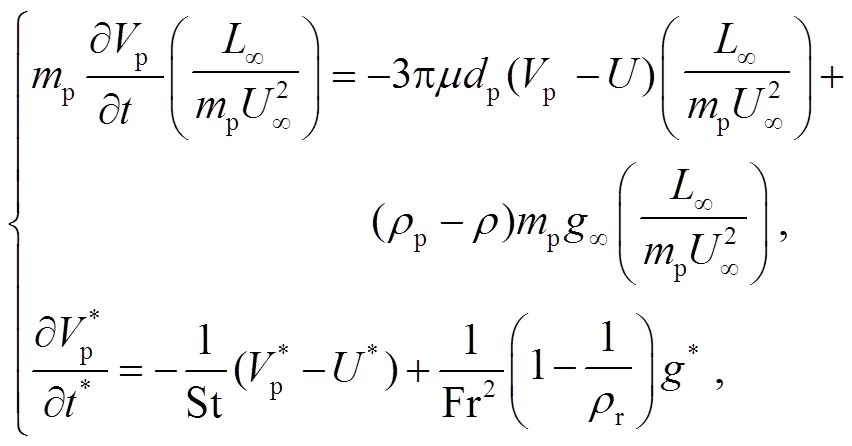
3.1.5 热泳力

由于极端力学条件下的壁流边界层存在温度梯度, 细小的颗粒会受到温度梯度诱导的热泳力[8]影响。式(16)为考虑 Stokes 阻力和热泳力的方程, 式(17)为理论解。图 11 显示, 本文 PP-DNS 结果与理论解(式(17))吻合。

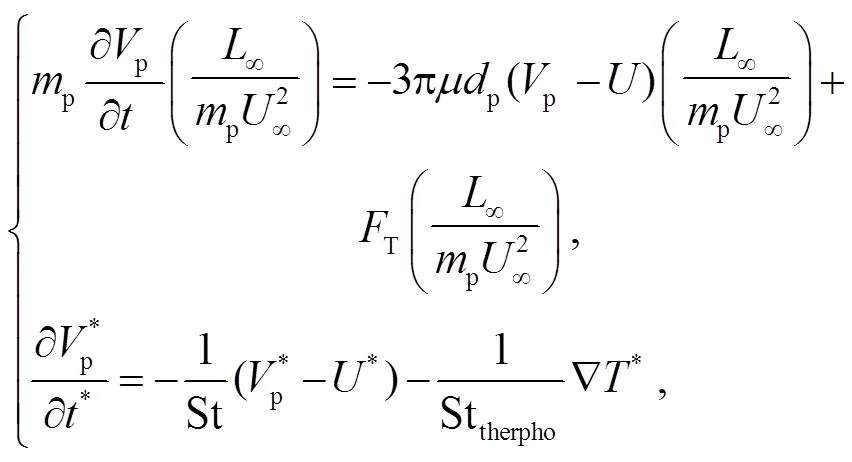
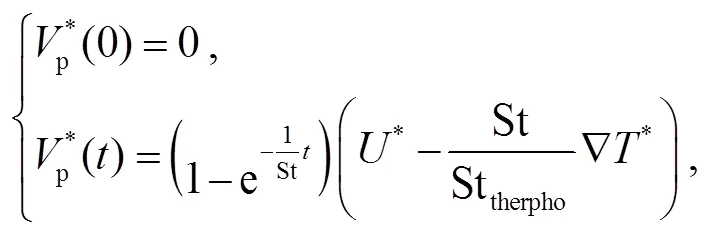
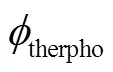
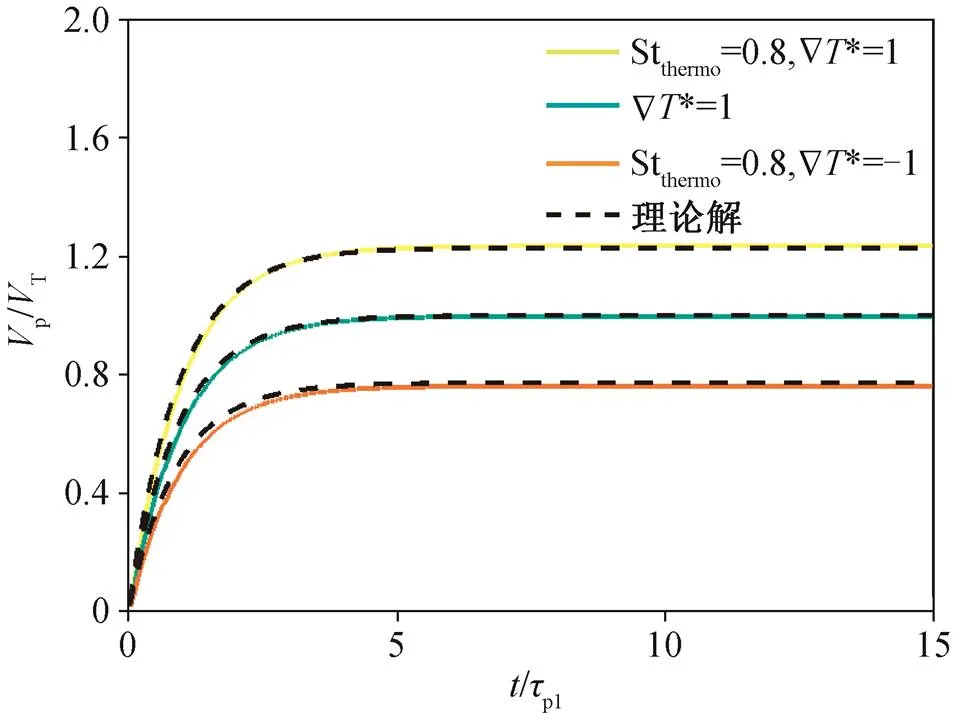
图11 受到热泳力的惯性颗粒在均匀流中的非定常速度与理论解的验证

3.1.6 电场力

在极端力学环境下, 颗粒群间的碰撞会产生局部电场[4,58], 因此带电颗粒动力学不可忽略。本文不考虑颗粒群相互碰撞产生的动态电场, 只考虑电场是常矢量的情况。式(18)为考虑 Stokes 阻力和电场力的方程, 式(19)为理论解[8]。图 12 显示, 本文PP-DNS 结果与理论解(式(19))吻合。

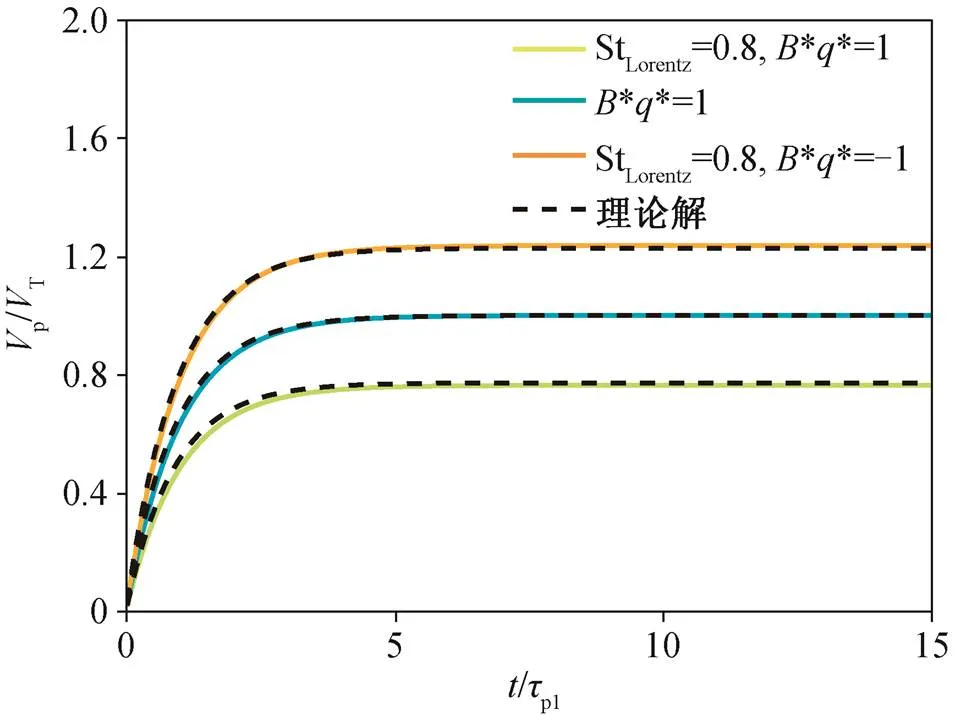
图13 受到磁场力的惯性颗粒在均匀流中的非定常速度与理论解的验证

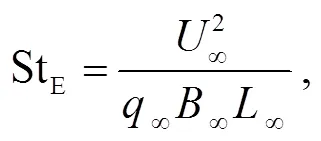
3.1.7 磁场力

根据经典电磁理论, 带电颗粒群运动会感生动态电磁场。当前暂时不考虑颗粒群相互碰撞产生的动态电磁场, 只考虑磁场是常矢量的情况。式(20)为考虑 Stokes 阻力和磁场力的方程, 式(21)为理论解[8]。图 13 显示, 本文 PP-DNS 结果与理论解(式 (21))吻合。

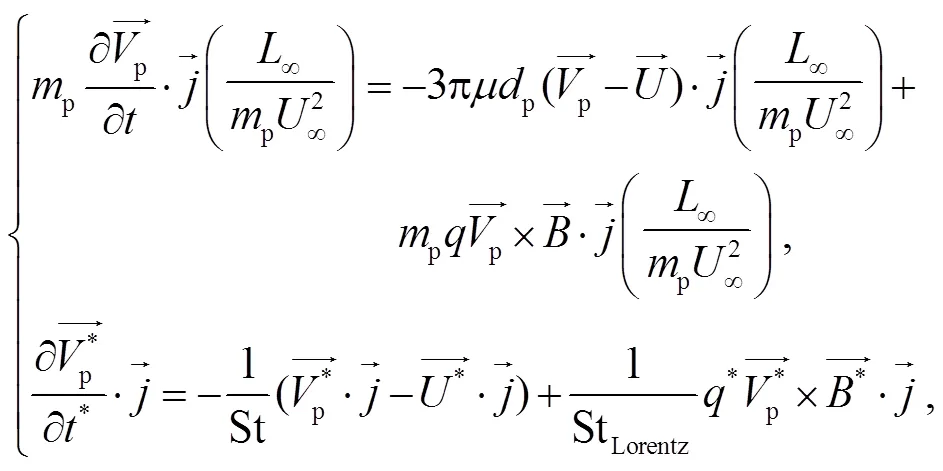
表3 可压缩槽道流的DNS流场参数设置

图15 单相可压缩槽道湍流Reτ=150的湍流一阶矩和二阶矩验证

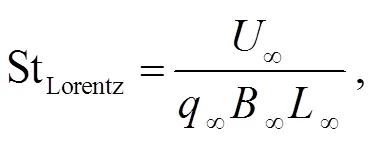
3.1.8 热对流

圆球在可压缩流动中的对流热交换系数会被可压缩效应修正[3,8,52]。式(22)为考虑热对流效应的颗粒热力学方程, 式(23)为理论解[8]。图 14 显示, 本文 PP-DNS 结果与理论解(式(23))吻合。

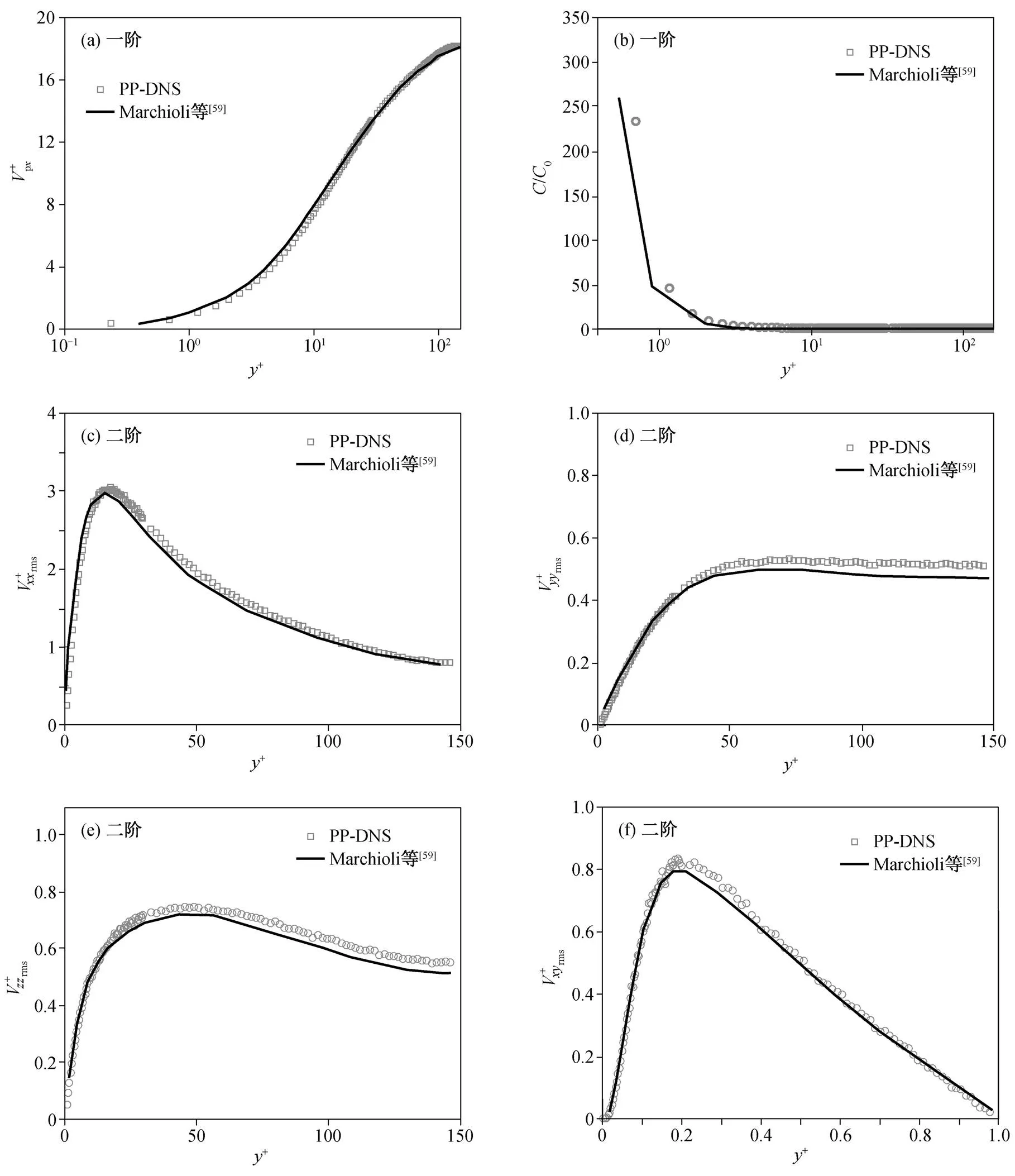
图16 弥散颗粒相St+=25的一阶和二阶统计矩验证

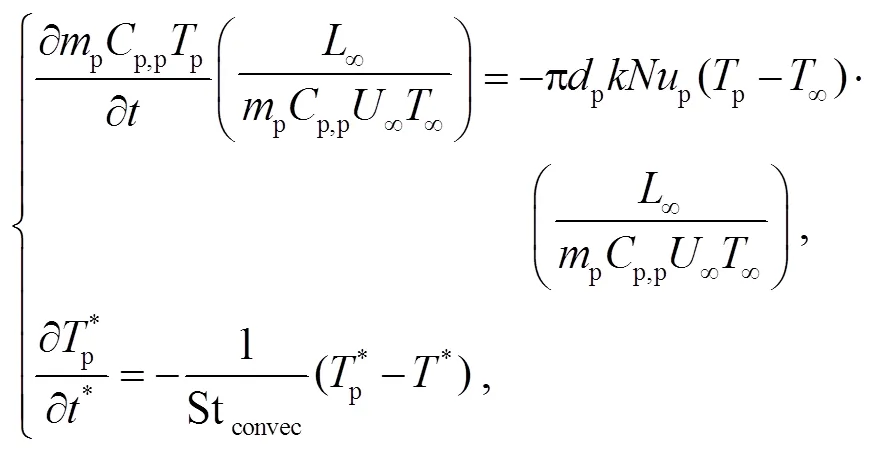
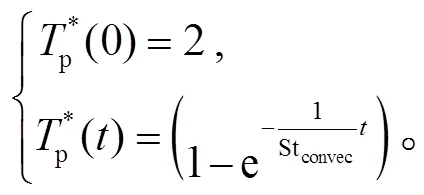
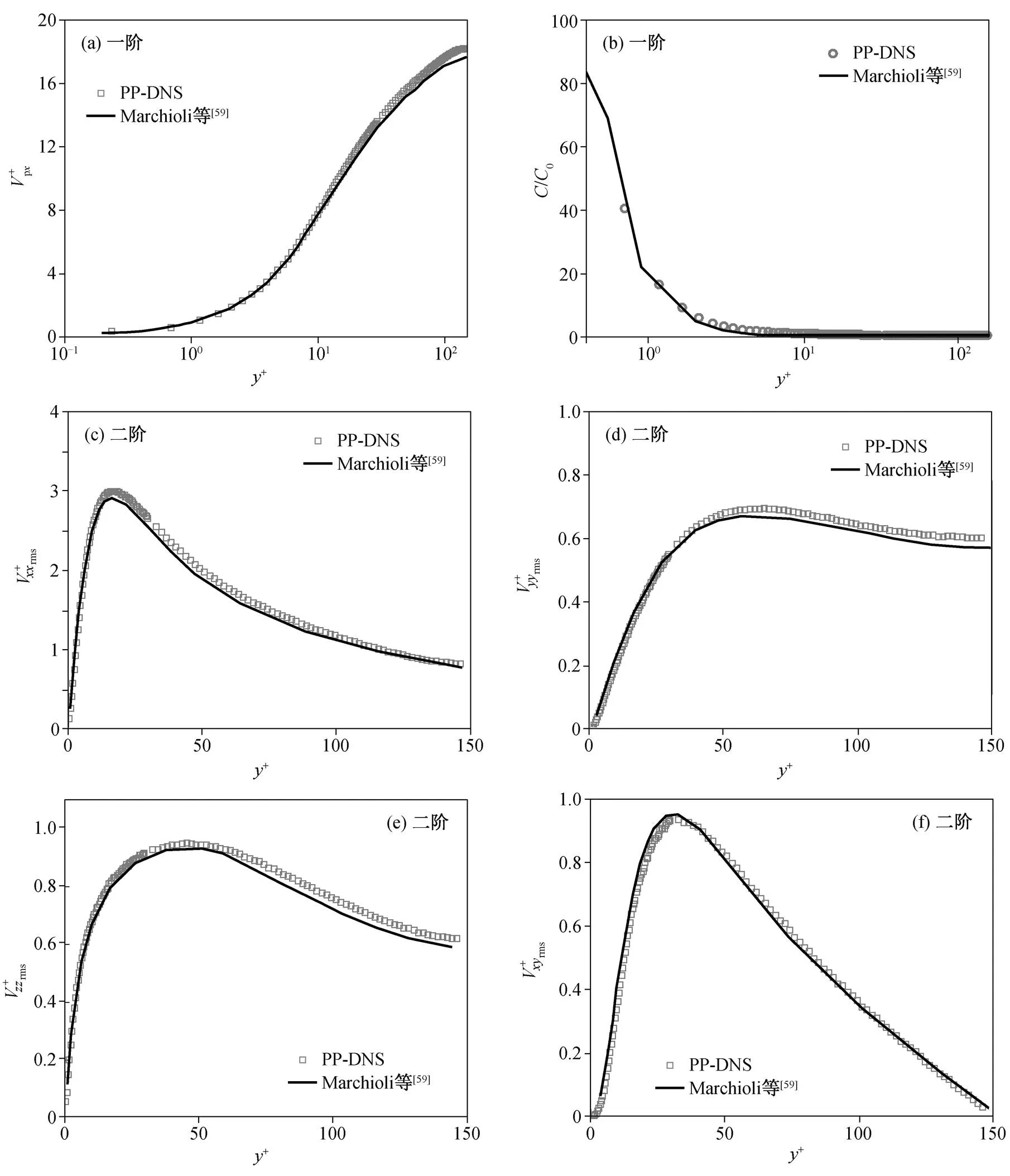
图17 弥散颗粒相St+=5的一阶和二阶统计矩验证

综上所述, 单颗粒验证问题本质上分为两个方面。1)部分模块采用单向耦合。任何形式的 Bug 和错误都与流体求解器无关, 因此可以很好地锁定由编程错误带来 Bug 的位置, 提高编程效率。2)相间阻力和热对流模块采用双向耦合。这是因为根据理论方程, 尽管多物理效应复杂, 但其反馈到携带流体相的路径是唯一确定的[8,39], 即颗粒动力学方程只能通过相间阻力反馈到流体动量方程中, 多物理效应只能通过改变相间阻力, 间接地调制流体动量。同理, 颗粒热力学方程只能通过热对流反馈到流体能量方程中, 热辐射效应只能通过改变热对流, 间接地调制流体能量。从算例结果可知, 本文可压缩颗粒两相流求解器可以很好地数值模拟点力颗粒在极端力学环境中的动力学和热力学过程, 并能实现两相耦合。

图18 弥散颗粒相St+=1的一阶和二阶统计矩验证

3.2 颗粒群问题

3.2.1数值标模1

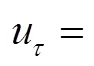
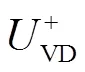
表4 可压缩槽道流Ma=0.3, Reτ=180的DNS流场参数设置

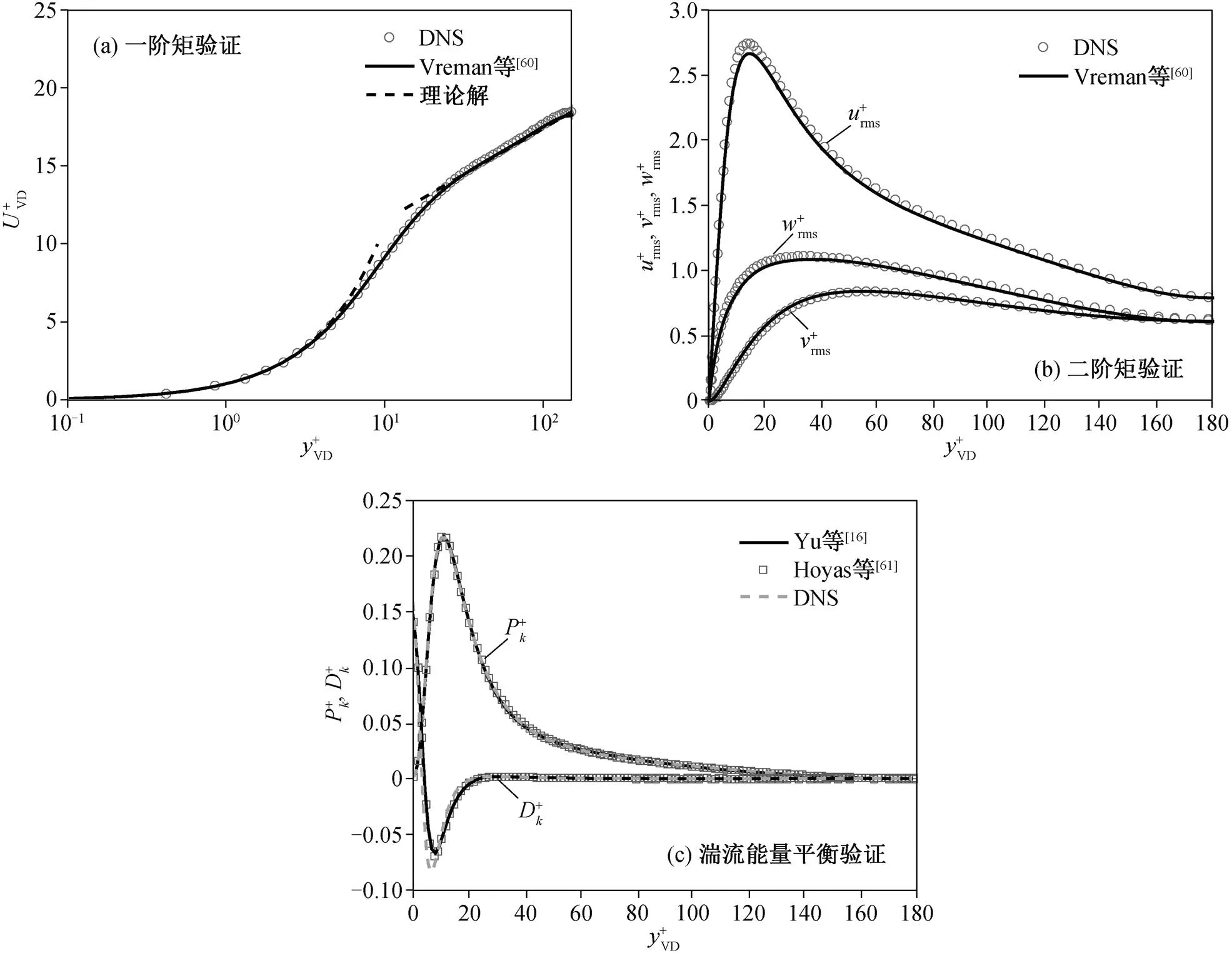
图19 单相可压缩槽道湍流Reτ=180的湍流一阶矩、二阶矩验证和湍流能量平衡验证

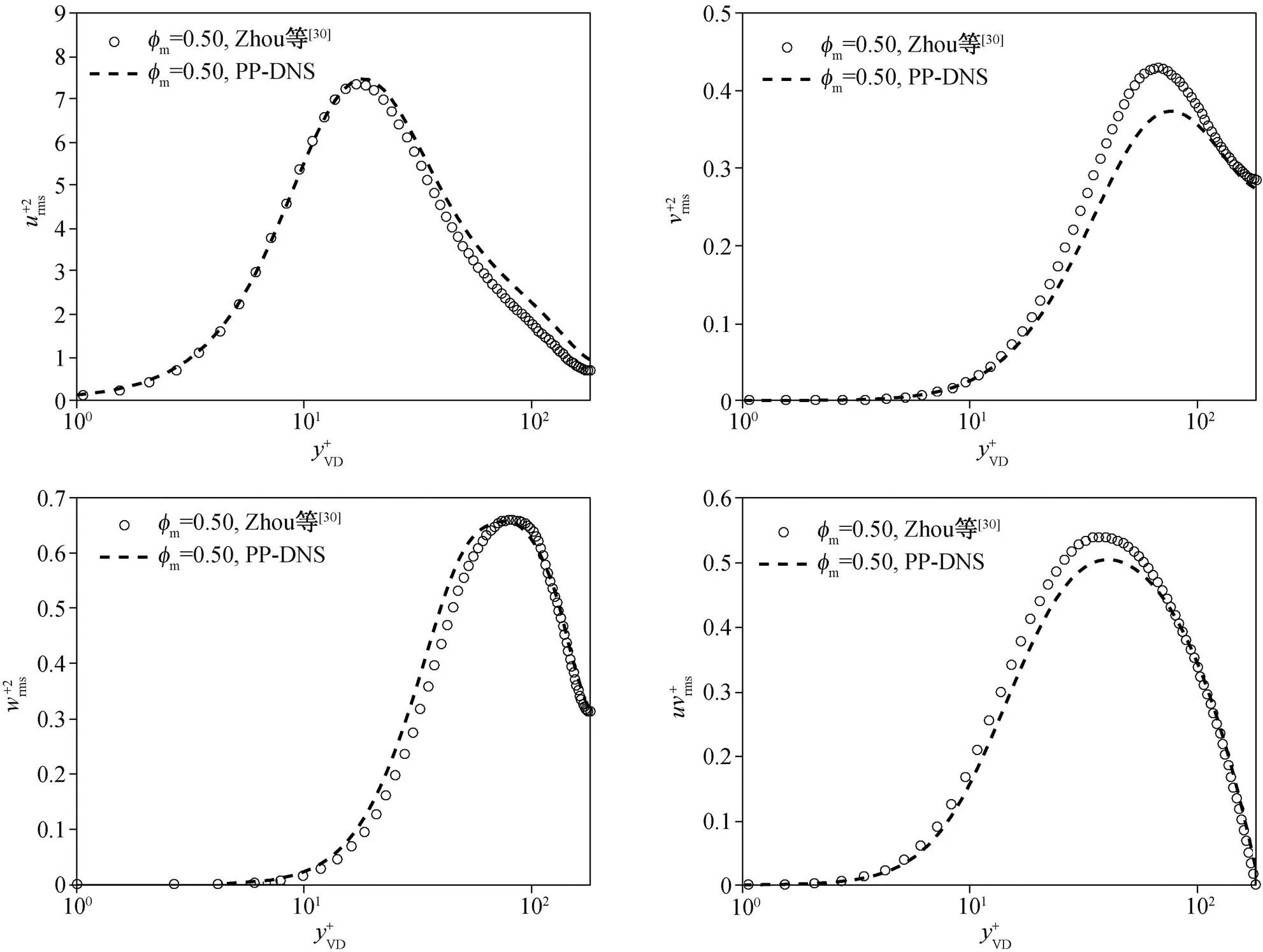
图20 槽道颗粒湍流Reτ=180, =0.50脉动速度验证

3.2.2数值标模2

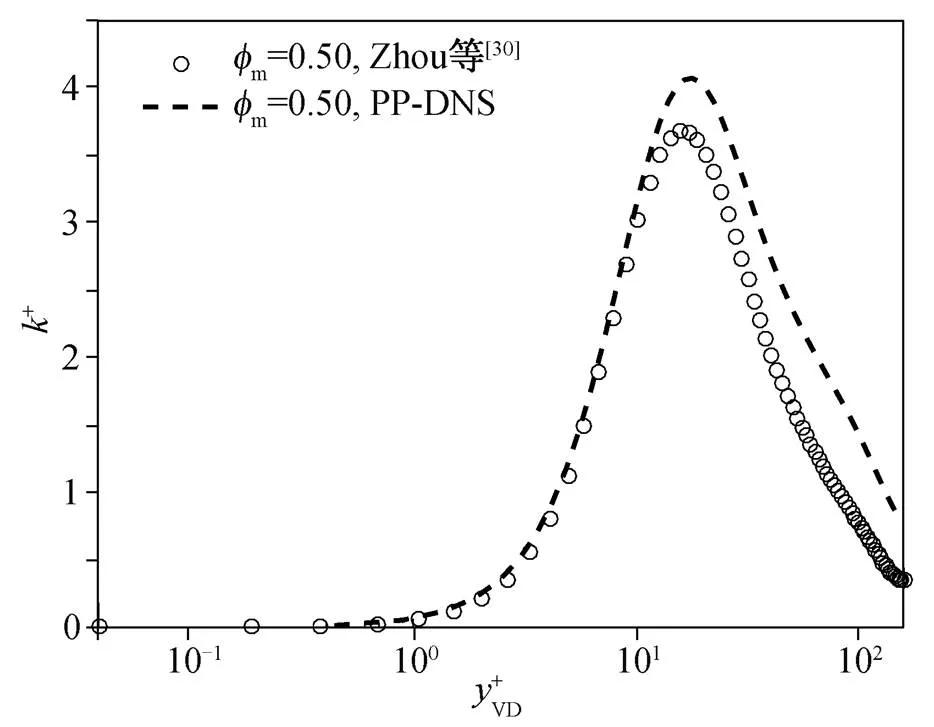
图21 槽道颗粒湍流Reτ=180, =0.50湍动能验证

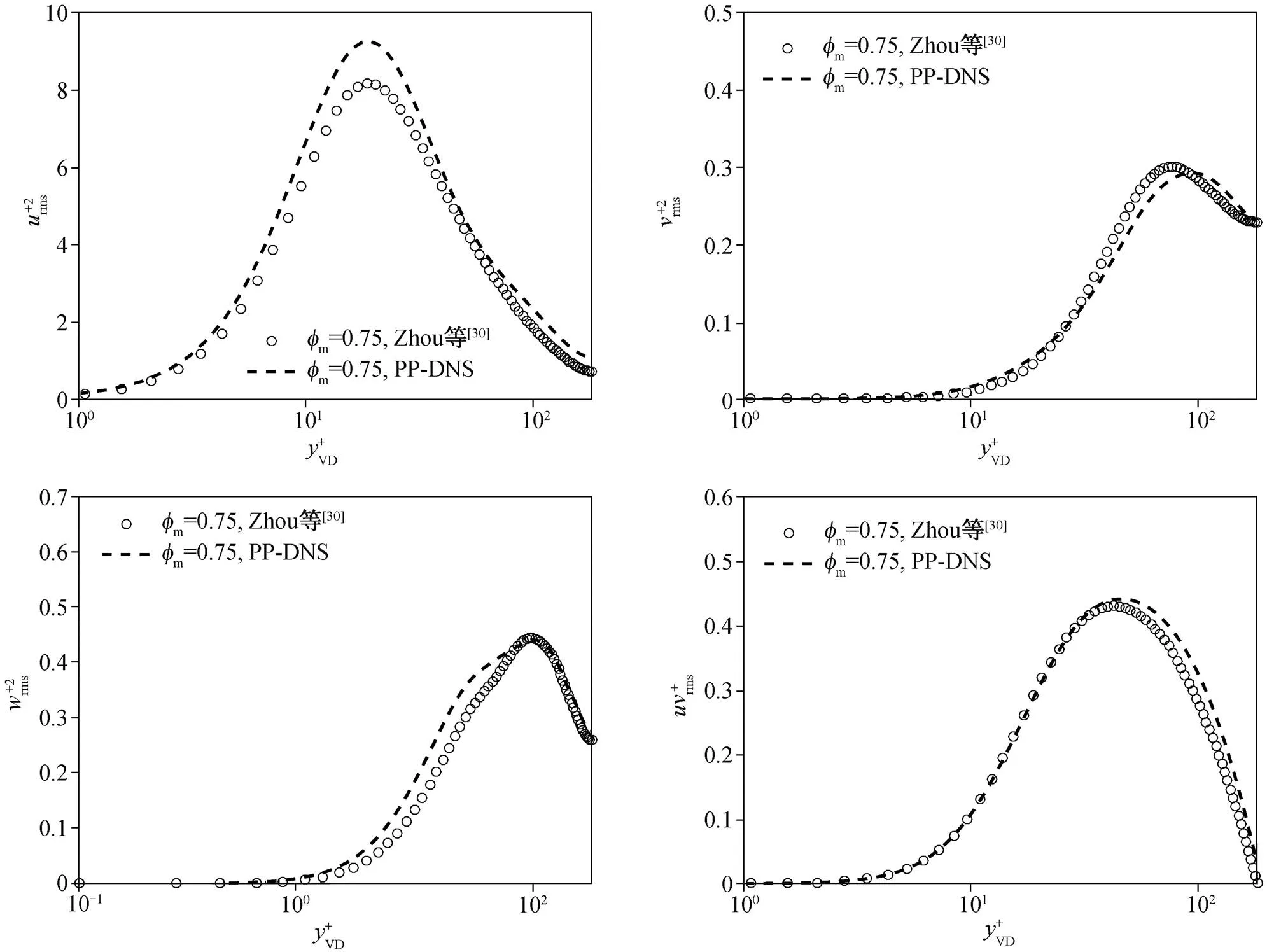
图22 槽道颗粒湍流Reτ=180, =0.75脉动速度验证

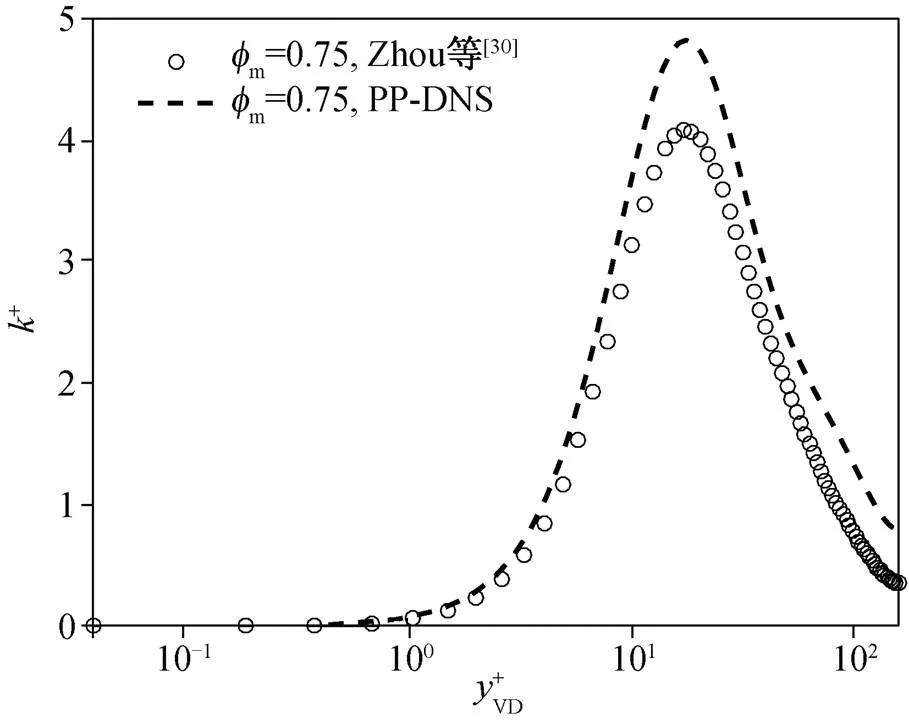
图23 槽道颗粒湍流Reτ=180, =0.75湍动能验证

4 并行效率

以表 3 的参数设置为例, 在 Re=180, Ma=0.3,p=105的条件下, 考察不同并行核数和不同量级的颗粒数目对颗粒两相流求解器并行综合效率的影响。图 24 对比颗粒两相流求解器与单独携带流体相求解器的并行运行时间和加速度比。可以看出, 本文开发的颗粒两相流求解器的绝对运行时间和加速比与流体求解器相差不大。图 25 对比两者的并行效率[39]和颗粒求解器的计算增量。可以看出, 两者的并行效率基本上相同, 且颗粒两相流求解器导致的计算增量为 30%。

以表 3 中算例的颗粒数目p=105为基准, 考察Re=180, Ma=0.3 条件下, 不同颗粒数目p=105, 107,108(“超载”)和不同并行核数对并行综合效率的影响, 结果如图 26 所示。可以看出, 颗粒两相流求解器的运行时间随着运行核数的增加而线性下降, 相对于标准算例p=105的运行时间, “超载”算例的运行时间随着颗粒数据增加而线性增加。颗粒求解器并行效率的线性特性体现了动态链表数组在求解颗粒数目巨大问题上的并行优势。与全局数组相比, 颗粒数目增加带来的并行效率是非线性降低的, 甚至会因为占用的内存太多而导致内存溢出, 使得算例无法进行。

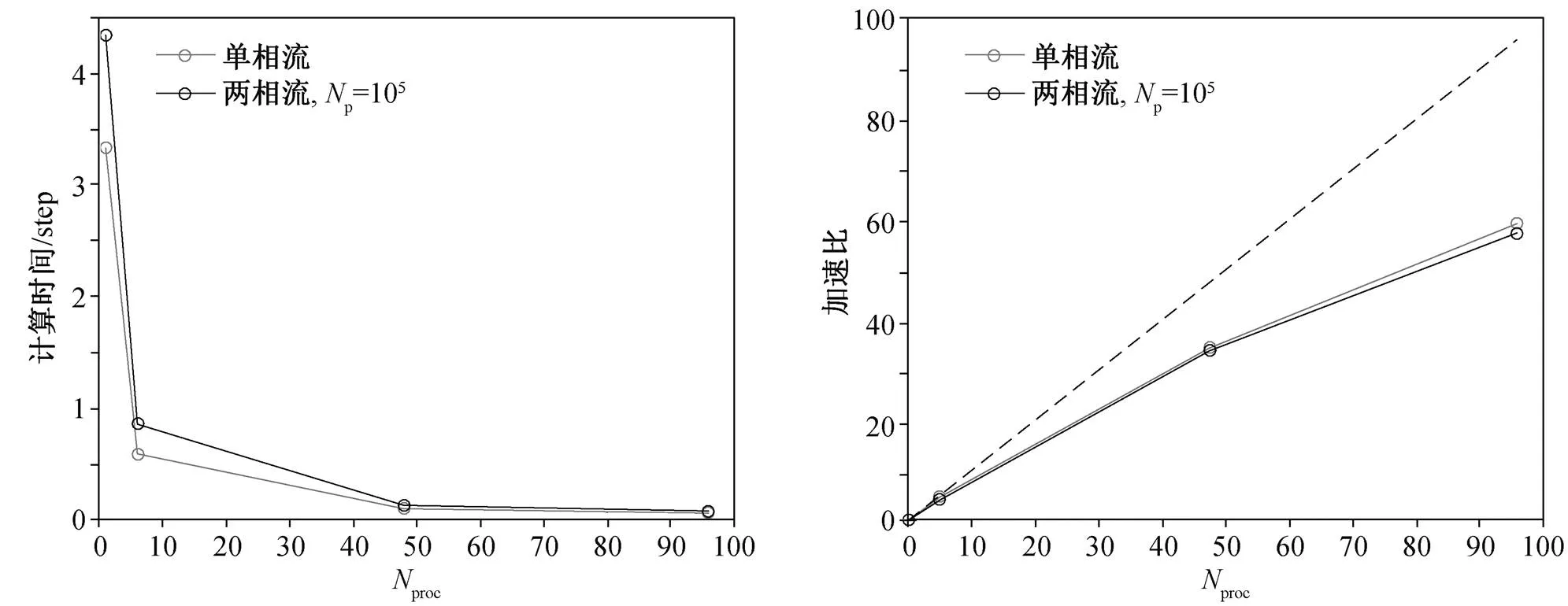
图24 可压缩槽道颗粒湍流的并行计算时间和加速比与分块数目的关系

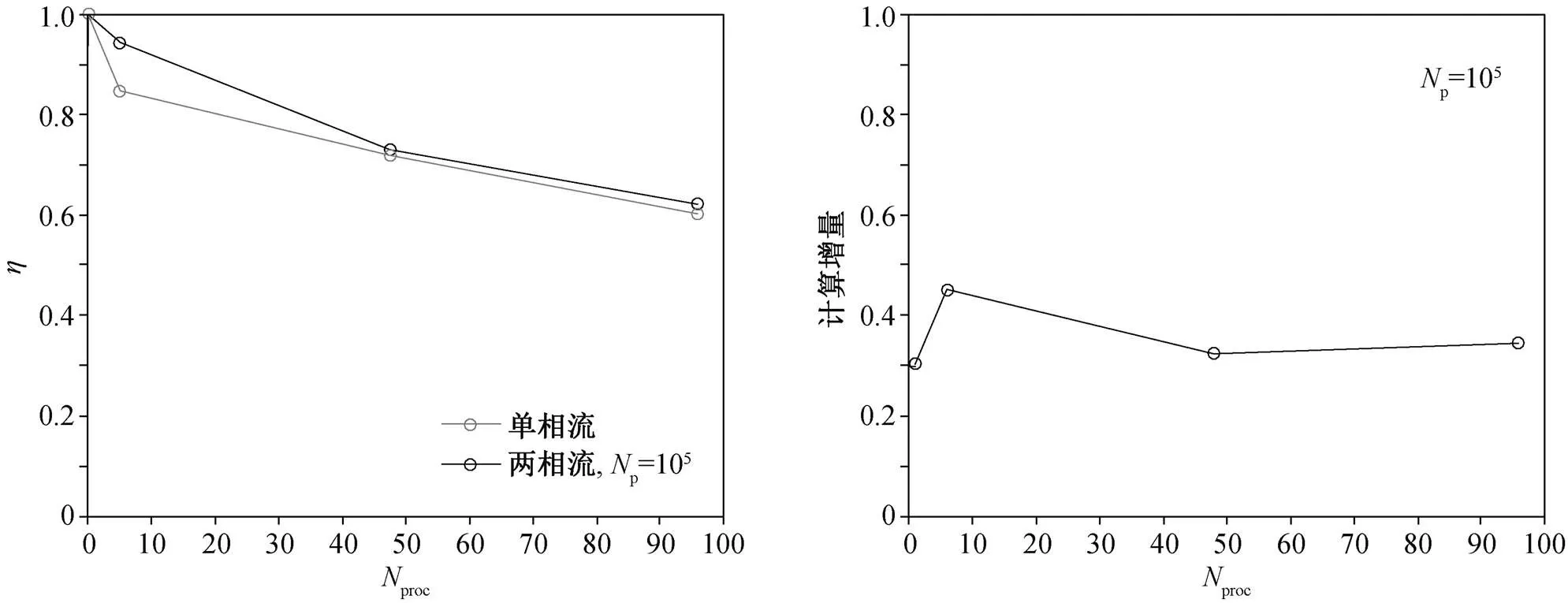
图25 可压缩槽道颗粒湍流的并行计算效率η和颗粒求解器的计算增量与分块数目的关系

图26 可压缩槽道颗粒湍流的并行计算时间和加速比与分块数目的关系

5 结论和展望

本研究开发了一种基于点力模型的含颗粒可压缩流直接数值模拟求解器, 并与当前工业需求密切相关的多物理效应模块进行验证。采用动态链表数组对弥散相颗粒群进行内存分配, 使得每个 MPI 并行分块使用的内存是全局数组分配方式的 1/。并行分块数目越大, 基于动态链表数组的颗粒求解器相对于全局数组的内存利用效率越高。理论分析表明, 对于颗粒碰撞问题, 动态链表数组的颗粒求解器的计算量是全局数组的 1/2。本文检验了不同MPI 分块间的动态链表数组通信, 并对多物理效应的可压缩颗粒两相流求解器进行验证。在流动马赫数渐进趋于零的情况下, 对不可压颗粒湍流标模进行湍流各阶统计矩的验证。颗粒并行求解器采用动态链表技术, 对弥散颗粒相进行分块内存分配以及逻辑层次封装技术, 提高了计算效率并节约了内存, 使得颗粒并行求解器具备向 GPU 版本拓展的可 能性。

可压缩颗粒解析的直接数值模型算法涉及大量拉格朗日点的信息反馈到局部欧拉点[16], 导致局部的欧拉点“接收”到大量不同来源的数值间断, 从而增加可压缩颗粒两相流求解器的数值刚性。因此, 在未来的研究中, 一方面需要增加压力修正的数值算法模块来稳定可压缩颗粒两相流求解器, 另一方面, 需要增加多重网格算法对求解器进行加速来解决由于数值刚性带来的计算量大的问题。

[1] Crowe C T, Schwarzkopf J D, Sommerfield M, et al. Multiphase flows with droplets and particles. Multi-phase flows with droplets and particles. Boca Raton: CRC Press, 2011

[2] 岳朋涛. 超燃冲压发动机燃烧室若干问题的研究[D]. 北京: 中国科学技术大学, 2002

[3] 李婷婷, 刘朋欣, 袁先旭, 等. 高焓可压缩流动热辐射颗粒两相流理论分析. 北京大学学报(自然科学版), 2022, 58(6): 989–998

[4] 胡文文. 风沙流中沙粒带电机理及荷质比研究[D]. 兰州: 兰州大学, 2012

[5] Zheng Xiaojing, He Lihong, Zhou Youhe. Theoretical model of the electric field produced by charged parti-cles in windblown sand flux. Journal of Geophysical Research-Atmospheres, 2004, 109: D15208

[6] Zamansky R, Coletti F, Massot M, et al. Radiation induces turbulence in particle-laden fluids. Physics of Fluids, 2014, 26(7): 071701

[7] Healy D P, Young J B. An experimental and theoretical study of particle deposition due to thermophoresis and turbulence in an annular flow. International Journal of Multiphase Flow, 2010, 36(11/12): 870–881

[8] 李青, 涂国华, 李婷婷, 等. 高焓流动中的可压缩颗粒求解器(第 1 部分): 考虑多物理效应的点力颗粒两相流理论方程. 空气动力学学报, 2023, 41(8): 71–86

[9] Li Xinliang, Fu Dexun, Ma Yanwen. Direct numerical simulation of a spatially evolving supersonic turbulent boundary layer at Ma=6. Chinese Physics Letters, 2006, 23(6): 1519–1522

[10] Hirsch C. Numerical computation of internal and ex-ternal flows. New York: John Wiley & Sons Inc, 1988

[11] 应隆安, 滕振寰. 双曲型守恒律方程及其差分方法. 北京: 科学出版社, 1991

[12] 谷超豪. 数学物理方程. 第3版. 北京: 高等教育出版社, 2012

[13] Pierce C D. Progress-variable approach for large-eddy simulation of turbulent combustion [D]. Stanford: Stan-ford University, 2001

[14] Yu Zhaosheng, Shao Xueming. A direct-forcing fic-titious domain method for particulate flows. Journal of Computational Physics, 2007, 227(1): 292–314

[15] Mehrabadi M, Horwitz J, Subramaniam S, et al. A direct comparison of particle-resolved and point-particle methods in decaying turbulence. Journal of Fluid Mechanics, 2018, 850: 336–369

[16] Yu Zhaosheng, Xia Yan, Guo Yu, et al. Modulation of turbulence intensity by heavy finite-size particles in upward channel flow. Journal of Fluid Mechanics, 2021, 913: A3

[17] 李瑞元, 陈飞国, 葛蔚, 等. 高马赫数低雷诺数条件下圆球绕流曳力系数. 空气动力学学报, 2021, 39(3): 201–208

[18] Maxey M R. Equation of motion for a small rigid sphere in a nonuniform flow. Physics of Fluids, 1983, 26(4): 883–889

[19] Balachandar S, Eaton J K. Turbulent dispersed multi-phase flow. Annual Review of Fluid Mechanics, 2010, 42: 111–133

[20] 袁先旭, 陈坚强, 杜雁霞, 等. 国家数值风洞(NNW)工程中的CFD基础科学问题研究进展. 航空学报, 2021, 42(9): 625733–625733

[21] 陈坚强. 国家数值风洞(NNW)工程关键技术研究进展. 中国科学: 技术科学, 2021, 51(11): 1326–1347

[22] Wang Lianping, Maxey M. Settling velocity and con-centration distribution of heavy particles in homoge-neous isotropic turbulence. J Fluid Mech, 1993, 256 (1): 27–68

[23] Rosa B, Parishani H, Ayala O, et al. Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution DNS. International Journal of Multiphase Flow, 2016, 83: 217–231

[24] Ferrante A, Elghobashi S. Reynolds number effect on drag reduction in a microbubble-laden spatially deve-loping turbulent boundary layer. Journal of Fluid Me-chanics, 2005, 543(1): 93–106

[25] Lain S, Sommerfield M. Euler/Lagrange computations of pneumatic conveying in a horizontal channel with different wall roughness. Powder Technology, 2008, 184(1): 76–88

[26] Marchioli C, Soldati A. Mechanisms for particle trans-fer and segregation in a turbulent boundary layer. Jour-nal of Fluid Mechanics, 2002, 468: 283–315

[27] Daitche A. On the role of the history force for inertial particles in turbulence. Journal of Fluid Mechanics, 2015, 782: 567–593

[28] Zamansky R, Coletti F, Massot M, et al. Turbulent thermal convection driven by heated inertial particles. Journal of Fluid Mechanics, 2016, 809: 390–437

[29] Zhao Lihao, Andersson H I, Gillissen J. Interphasial energy transfer and particle dissipation in particle-laden wall turbulence. Journal of Fluid Mechanics, 2013, 715(1): 32–59

[30] Zhou Tian, Zhao Lihao, Huang Weixi, et al. Non-monotonic effect of mass loading on turbulence modulations in particle-laden channel flow. Physics of Fluids, 2020, 32(4): 043304

[31] Pan Qingqing, Xiang Hong, Wang Ze, et al. Kinetic energy balance in turbulent particle-laden channel flow. Physics of Fluids, 2020, 32(7): 073307

[32] Li Dong, Luo Kun, Fan Jianren. Modulation of tur-bulence by dispersed solid particles in a spatially de-veloping flat-plate boundary layer. Journal of Fluid Mechanics, 2016, 802: 359–394

[33] Dai Qi, Luo Kun, Jin Tai, et al. Direct numerical simulation of turbulence modulation by particles in compressible isotropic turbulence. Journal of Fluid Mechanics, 2017, 832: 438–482

[34] Xiao Wei, JinTai, Luo Kun, et al. Eulerian-Lagrangian direct numerical simulation of preferential accumu-lation of inertial particles in a compressible turbulent boundary layer. Journal of Fluid Mechanics, 2020, 903: A19

[35] Wang Lianping, Wexler A S, Zhou Y. Statistical me-chanical description and modelling of turbulent colli-sion of inertial particles. Journal of Fluid Mechanics, 2000, 415: 117–153

[36] Fevrier P, Simonin O, Squires K D. Partitioning of particle velocities in gas-solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical stu-dy. Journal of Fluid Mechanics, 2005, 533: 1–46

[37] Yu Wenchao, Fede P, Yazdanpanah M, et al. Gas-solid fluidized bed simulations using the filtered approach: validation against pilot-scale experiments. Chemical Engineering Science, 2020, 217: 115472

[38] Marchioli C. Large-eddy simulation of turbulent dis-persed flows: a review of modelling approaches. Acta Mechanica, 2017, 228(3): 741–771

[39] Tian Baolin, Zeng Junsheng, MengBaoqing, et al. Com-pressible multiphase particle-in-cell method (CMP-PIC) for full pattern flows of gas-particle system. Journal of Computational Physics, 2020, 418: 109602

[40] Martin J E, Meiburg E. The accumulation and disper-sion of heavy particles in forced two-dimensional mixing layers. I. The fundamental and subharmonic cases. Physics of Fluids, 1994, 6(3): 1116–1132

[41] 李新亮, 马延文, 傅德薰. 可压槽道湍流的直接数值模拟及标度律分析. 中国科学: A辑, 2001, 31(2): 153–164

[42] 童福林, 周桂宇, 周浩, 等. 激波/湍流边界层干扰物面剪切应力统计特性. 航空学报, 2019, 40(5): 122504–122504

[43] Mirjalili S, Mani A. Consistent, energy-conserving momentum transport for simulations of two-phase flows using the phase field equations. Journal of Computational Physics, 2019, 426: 109918

[44] Zhang Bo, Boyd B, Ling Y. Direct numerical simu-lation of compressible interfacial multiphase flows using a mass-momentum-energy consistent volume-of-fluid method. Computers & Fluids, 2022, 236: 105267

[45] Patankar S V. Numerical heat transfer and fluid flow. Boca Raton: CRC Press, 1980

[46] Kim J, Moin P. Turbulence statistics in fully developed channel flow at low Reynolds number. J Fluid Mech, 1987, 177: 133–166

[47] Lawrence C E. Partial differential equations. Rhode Island: American Mathematical Society, 1998

[48] Lele S K. Compact finite difference schemes with spectral-like resolution. Journal of Computational Phy-sics, 1992, 103(1) : 16–42

[49] Burden R L, Faires J D. Numerical analysis. 9th ed. Boston: Richard Stratton, 2011

[50] Bassenne M, Fu Lin, Mani A. Time-accurate and highly-stable explicit operators for stiff differential equations. Journal of Computational Physics, 2021, 424: 109847

[51] Loth E. Compressibility and rarefaction effects on drag of a spherical particle. AIAA Journal, 2008, 46(9): 2219–2228

[52] 尚庆, 沈清, 庄逢甘. 超声速气流中简化微小液滴横向喷射的汽化过程探索. 空气动力学学报, 2011, 29(1): 1–9

[53] Basset A B. A treatise on Hydrodynamics. Nature, 1888, 40: 412–423

[54] Mei Renwei, Adrian R. Flow past a sphere with an oscillation in the free-stream velocity and unsteady drag at finite Reynolds number. Journal of Fluid Me-chanics, 1992, 237(1): 323–341

[55] Righetti M, Romano G P. Particle–fluid interactions in a plane near-wall turbulent flow. Journal of Fluid Mechanics, 2004, 505: 93–121

[56] Hout R V. Time-resolved PIV measurements of the in-teraction of polystyrene beads with near-wall-coherent structures in a turbulent channel flow. International Journal of Multiphase Flow, 2011, 37(4): 346–357

[57] 董双岭, 曹炳阳, 过增元. 作用在粒子上的热泳升力研究. 工程热物理学报, 2015, 36(5): 1063–1066

[58] Zheng Xiaojing. Electrification of wind-blown sand: recent advances and key issues. European Physical Journal E Soft Matter, 2013, 36(12): no. 138

[59] Marchioli C, Soldati A, Kuerten J, et al. Statistics of particle dispersion in direct numerical simulations of wall-bounded turbulence: results of an international collaborative benchmark test. International Journal of Multiphase Flow, 2008, 34,(9): 879–893

[60] Vreman A W, Kuerten J. Comparison of direct nu-merical simulation databases of turbulent channel flow at Re=180. Physics of Fluids, 2014, 26(1): 015102

[61] Hoyas S, Jiménez J. Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Physics of Fluids, 2008, 20(10): 101511

MPI Solver of Particle-Laden Compressible High Enthalpy Flow: Numerical Method and Validation

LI Qing1,2, YU Zhaosheng3, LIU Pengxin1, LI Tingting4, CHEN Jianqiang1, YUAN Xianxu1,†

1. State Key Laboratory of Aerodynamics, China Aerodynamics Research and Development Center, Mianyang 621000; 2. Tianmushan Laboratory, Hangzhou 310000; 3. School of Aeronautics and Astronautics, Zhejiang University, Hangzhou 310027; 4. School of Chemical Engineering and Technology, Xi’an Jiaotong University, Xi’an 710049; † Corresponding author, E-mail: yuanxianxu@cardc.cn

Based on the theoretical equations of compressible particle-laden flow in multi-physical conditions, a MPI-Particle Solver based on dynamic linked list array is developed, which is coupled with a compressible flow solver of carried phase. The dispersed particle phase is different from the carried fluid phase, the previous one is based on the Lagrange coordinate system, while the later one is based on the Euler coordinate system. The traditional way is to use the global array to assign the memory to the dispersed particle phase to achieve the transfer between two-phase, but at expense of low computational efficiency. This paper uses dynamic linked list array to allocate memory to dispersed particle phase, achieve both problems. A series of DNS validations with references case have been done, in terms of multi-physical effects and two canonical cases at incompressible limit.

dynamic linked list array; Lagrange/Euler coordinate system conversion; particle solver of particle-laden compressible flow