基于ABAQUS 的气动潜孔锤球齿碎岩及布齿优化
2024-01-30杨秋明夏柏如
杨秋明,周 兢,王 瑜,夏柏如,吴 浩
(1.中国地质大学(北京),北京 100083; 2.自然资源部深部地质钻探技术重点实验室,北京100083;3.中煤地第二勘探局集团有限责任公司,河北 涿州 072750; 4.中国煤炭地质总局,北京100038)
0 引言
从20 世纪以来,对资源开采和工程建设越来越趋向深部发展,大直径气动潜孔锤因能进行大孔径、高安全性的深孔高效钻进施工,受到了国内外机械钻探领域学者的广泛关注。潜孔锤钻头合理钻进参数与布齿是提高碎岩效率与延长钻头使用寿命的关键因素,以球齿碎岩机理为依据来研究钻进参数与布齿是一种十分重要的方法[1-3]。
以球齿碎岩机理来研究钻进参数与布齿[4-7]主要有试验、仿真、数学建模型3 种方法。朱丽红等[8]分析球齿压入岩石的过程,首先球齿与岩石接触岩石产生弹性变形,随着冲击应力增大,应力波会以球齿与岩石的接触点为球心成同心球的形状在岩石内部扩散,随着球齿进一步侵入岩石,会对球齿周围的岩石产生侧应力直至崩离,最后形成破碎坑;马晓青[9]进行自由落体冲击岩石试验,得出岩石在多次冲击下明显破碎增大的冲击功临界值,并记录每次压头侵入岩石的深度,发现随冲击功增大侵入深度也在增大;常玉军等[10]对岩石的冲击回转碎岩机理进行了试验研究,为Ø1200 mm 潜孔锤钻头的合理布齿及钻进参数的选择提供依据;李华等[11]从球齿碎岩机理出发,探讨了相邻球齿对碎岩效果的影响,确定最优齿间距为(D1+D2)/2;彭伟等[12]以单齿碎岩机理为依据,得出布齿间距与圈距,并根据钻进软、硬地层不同工程施工需求,设计出2 种不同布齿的钻头。
王圣林等[13]基于非线性接触动力学理论,运用ABAQUS 软件建立了活塞-气动潜孔锤钎头-岩石仿真模型,分析了冲击速度和回转速度对钎头冲击反力、侵入深度和破岩比功的影响,进而对工艺参数进行优选;徐瑞晗[14]通过动力学仿真软件ABAQUS 建立钻头-岩石的冲击模型,赋予钻头不同的冲击速度及转速,分析不同工况下作用在岩石不同方向上的力、岩石的应力以及钻进深度;陈亮[15]对比分析潜孔锤破岩转矩的理论计算方法,采用ANSYS 对潜孔锤球齿的破岩过程进行模拟,并通过工程实例的实测数据验证两种转矩计算模型与仿真分析的准确性,潜孔锤转矩理论计算模型与实际转矩结果和仿真结果较为接近,估算出潜孔锤的破岩转矩,得出钻进转矩与其他钻进参数的相关性;高阳[16]采用理论方法对该钻头破岩动力学问题进行了分析,采用ABAQUS 确定该潜孔锤的单次冲击功和钻速;方金[17]采用ANSYS 研究球齿对岩样的冲击随时间的变化过程,应力随时间的变化情况及岩石裂纹扩展情况,定性地描述岩石的破碎情况;Zhao 等[18]、李从保[19]、Jiang 等[20]通过球齿碎岩的数值模拟,分析应力波在岩石的传播规律,得出应力以半球形应力波的方式向岩石的各个方向传播,球齿周围冲击时易呈拉裂破坏,并发现持续冲击岩石会导致岩石内部出现细小裂纹,当裂纹发育到一定程度,会导致岩石破碎;Song 等[21]基于钻井试验台和数值计算,对冲击应力波的传播过程进行分析,通过电镜观测破碎坑的裂纹,得出随着岩石温度的升高,冲击能量传递效率大致呈下降趋势,破岩比能先增大后减小的规律;杨达[22]采用Ø19 mm 球齿对硬岩进行研究,通过试验台进行了不同冲击功的冲击实验并使用ABAQUS 模拟分析出应力波对岩石的破坏,并完成对Ø600 mm 大直径潜孔锤布齿。
Saadati[23]对冲击钻井的裂缝系统进行数值模拟,并进行冲击试验验证模拟,在考虑钻头与地层相互作用下对冲击钻削问题进行了建模;Richard 等[24]建立了考虑钻头的轴向和扭转振动,及其耦合下PDC 钻头切削岩石的模型,但其钻进参数不完整;Depouhon 等[25]对Richard 的数学模型进行改进,提出了一个完整的PDC 钻头钻进响应模型,并对模型钻进参数进行了完善。
目前对大直径气动潜孔锤球齿布齿研究只关注到球齿冲击岩石的破碎范围,没有考虑到应力波对破碎坑岩附近的强度下降,也没有将冲击与切削作用结合起来进行研究。本文采用ABAQUS 中显性动态分析对不同钻压与冲击功下的球齿冲击切削岩石进行模拟仿真,并构造应力波数学模型对其进行验证,来研究球齿破碎岩石的影响,同时根据破碎比功、侵入深度、破碎范围与应力影响范围等指标参数,进行岩石破碎规律的研究,从而优选钻进参数和布齿方案。
1 碎岩机理研究
1.1 弹塑性接触分析
接触应力和接触面积是描述冲击破碎过程中的基本参数。冲击过程中另外一个重要的参数是平均接触应力u,与接触应力L以及接触半径a有关,其中接触半径a指的是粒子和岩石实际接触的边缘距离粒子中心轴线的距离,关系式为:
基于弹塑性压入分析和牛顿定律,得到了力与位移之间的微分关系式,即:
式中:m——球齿的质量(分摊钻头质量);v——球齿的冲击速度;r——冲击坑的深度;L——接触应力。
依据Hill 等[26]的布氏硬度实验得到冲击非线性弹塑性分析模型,对模型接触应力进行了详细描述,并得出其解析:
式中:H——梅尔硬度;P——接触应力;K——梅尔定律常数;m——材料的应变硬化指数,为与岩石相关的材料常数;R0——球齿半径。
1.2 应力波数学模型建立
在球齿的冲击作用下,岩石内部产生的应力应变将以应力波球面波的形式传播。如图1 所示,球齿冲击岩石界面O点,从而使应力波从球齿表面向岩石中传播。由于球面波的对称性,在球坐标系(r,θ,φ)中,波动与θ和φ无关,所以∂/∂φ=∂/∂θ=0,v=w=0,径向位移u不为零。

图1 应力波球坐标示意Fig.1 Diagram of spherical coordinates of stress waves
根据球坐标,得应力-应变关系式为:
式中:εr、εθ——球坐标系下岩石的径向与周向应变。
根据广义虎克定律,假设岩石在受到损伤前为弹性体,得应力波的径向与周向应力的数学表达式:
式中:E——岩石的杨氏模量,Pa;μ——岩石的泊松比。
1.3 应用Matlab 解应力波数学模型
对岩石应力场的计算,可视为球腔受压的运动方程的求解问题[27],由于应力波呈球极对称性,波动的场变量只有波半径r和时间t,唯一的变量沿径向,设为u(r,t)。其边界条件与初始条件为:
负号代表受压,对球坐标微元体dθdr的动量守恒,得到用位移表示的球面波的运动方程:
式中:c1——弹性纵波在岩石中的传播速度,m/s。
从上述公式中已知边界条件与应力波的控制方程,利用Matlab 中的PDE 偏微分工具对u(r,t)进行求取,再将其代入应力表达式中,得出应力波在岩石中的应力值,由于在仿真中得到的应力曲线为Mis‑es 等效应力,所以对数学模型数据进行处理,得到σm曲线图如图2 所示,随着距离冲击源越来越远,应力波峰值在逐渐降低,曲线先减后增再趋向平缓。最开始球齿冲击对周围岩石产生压应力;在随着应力波的作用,压应力逐渐转为拉应力,导致总应力逐渐减小;当转化完成时,总应力达到另一峰值;最后由于应力波作用消散,其应力趋于平稳。

图2 数学模型σm 应力曲线Fig.2 Mathematical model σm stress curve
2 单球齿冲击碎岩数值模拟
2.1 有限元模型的建立
对于Ø711 mm 大直径潜孔锤,所用球齿直径18 mm、高24 mm。采用ABAQUS 模拟软件,为确保模拟的准确性,本文采用三维模型进行模拟分析,确保岩石受冲击时应力波对岩石边界不会造成剧烈反弹,将岩石的长宽设计为球齿直径的16 倍,高为7倍,为300 mm×130 mm。模拟采用了在岩石模型的网格单元之间插入了0 厚度的Cohesive 粘结单元[28],该设置会使岩石受冲击时进行随机的裂纹扩展。相互作用采用通用接触,再对球齿与岩石的接触进行独立的属性指派损伤与粘性行为。为提高运算效率,对球齿与岩石接触的中心进行了局部网格加密划分。岩石的网格类型为三维应力C3D6;Cohesive 网格为粘性COH3D8。花岗岩模型共划分了202240 个网格。单球齿冲击模型网格划分见图3。
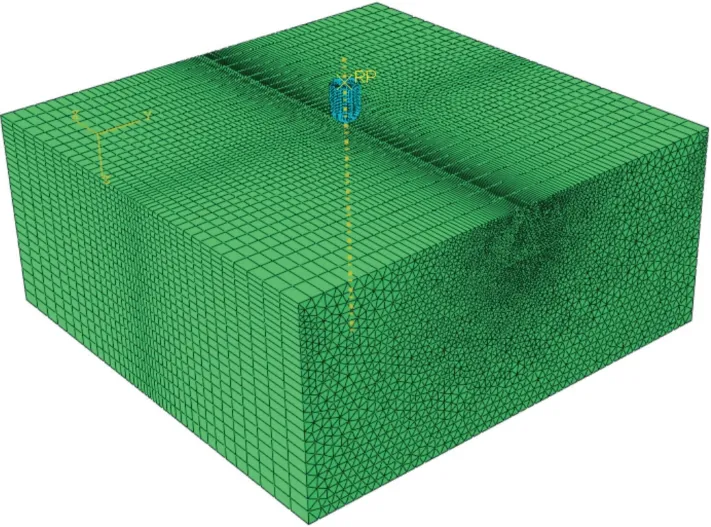
图3 单球齿冲击模型网格划分Fig.3 Single spherical tooth impact model meshing
大直径潜孔锤主要运用在破碎硬岩地层中,此次仿真的岩石为花岗岩,花岗岩与球齿主要物理属性见表1[29]。其抗压强度120 MPa,抗拉强度10.5 MPa,抗剪强度21.2 MPa。
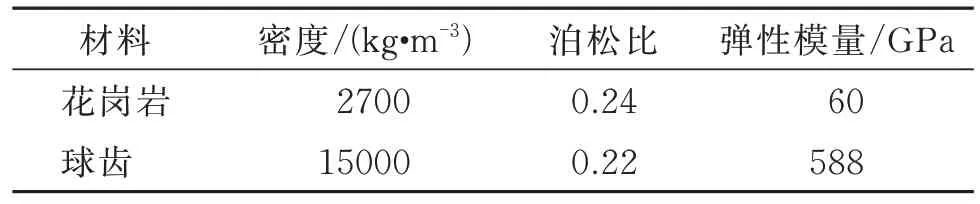
表1 花岗岩与球齿参数Table 1 Granite and spherical tooth parameters
2.2 模型验证
如图4 所示,仿真模拟取的是距冲击源为36 mm 处半球面上几点的平均应力曲线,得出两曲线的趋势是相同的,仿真应力曲线整体处于下方且应力趋于稳定时是动态稳定。原因为仿真模型考虑了应力波对破碎岩石的作用,会对应力波的能量造成削弱,也因岩石不是无限边界导致应力波会遇到边界发生反射,但岩石模型取设计得足够大,该反射影响不大。
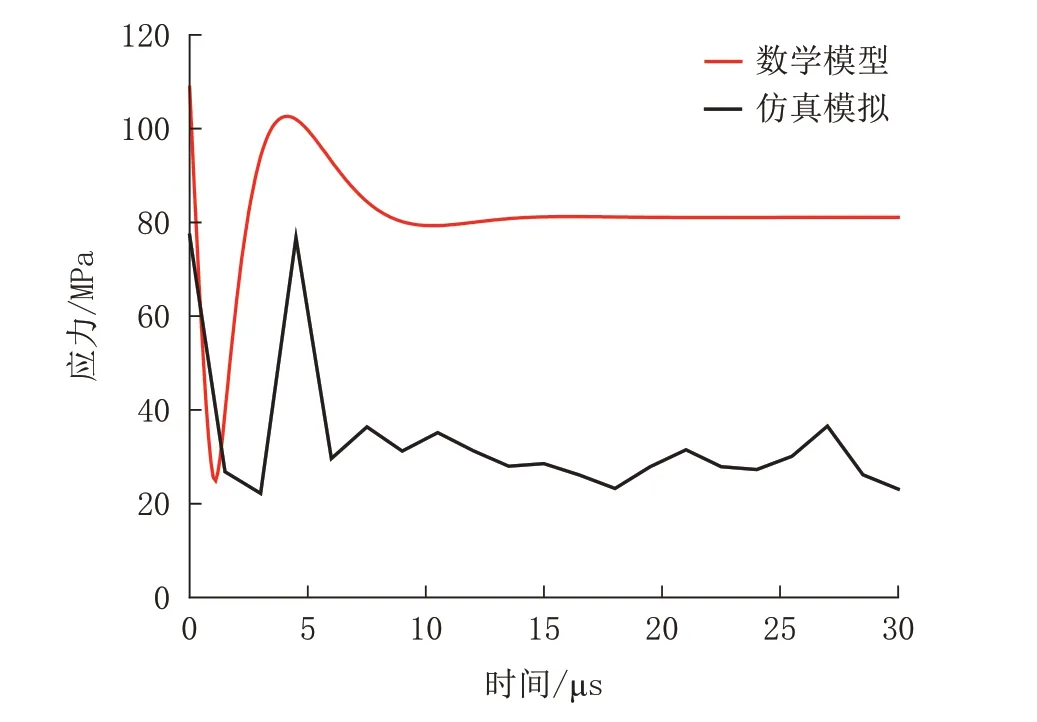
图4 数学模型与仿真模拟应力曲线Fig.4 Mathematical models and simulations simulate stress curves
2.3 单球齿数值分析
2.3.1 破碎比功研究
进行了20 组不同钻压与冲击功的数值模拟,通过软件记录到每一次破碎体积(见图5)。从钻压的角度来看,岩石的破碎体积随钻压的升高不断的增大,可以得出钻压增大对破碎岩石有一定的增强,但是当达到1.4 kN 之后钻压对岩石的影响很小。从冲击功的角度来看,随着冲击功不断增大其破碎体积也是不断在增大的,但是在30~40 J 之间,特别是30~35 J 的破碎体积是相差最大的,可以见得,冲击功破碎岩石体积增幅最大的参数为30~40 J 之间。
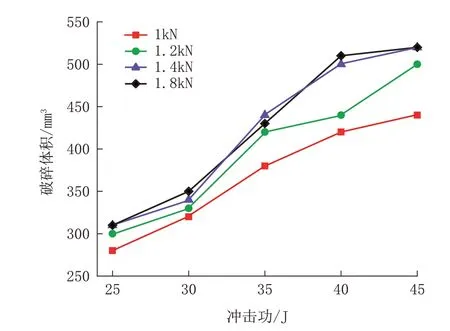
图5 单球齿冲击破碎体积Fig.5 Single spherical tooth impact crushing volume
为更加了解岩石破碎效率,进行了破碎比功的研究(见图6)。其趋势与破碎体积不同,可以把其看为岩石破碎体积曲线的斜率,其为对冲击功的利用效率;当钻压为1.4 kN 时,其曲线处于较下方,冲击功的利用率较高,在冲击功35 J 时破岩效率最高;钻压为1.8 kN 时,冲击功40 J 时为整图效率最高一点。因此采取钻压为1.4 kN、冲击功在35 J,和钻压为1.8 kN、冲击功为40 J 的冲击参数较为优秀。

图6 单球齿冲击破碎比功Fig.6 Single spherical tooth impact crushing energy
2.3.2 球齿入岩位移研究
球齿入岩位移的研究,可得球齿的入岩深度与钻压和冲击功的关系,进而优选钻进参数,是对破碎坑的纵向破坏研究的重要指标参数。对球齿的入岩分析分别从钻压与冲击功两个角度去研究。图7 所示为在1.4 kN 钻压下,不同冲击功下的球齿入岩位移。

图7 1.4 kN 钻压不同冲击功下球齿位移曲线Fig.7 Spherical tooth displacement curve under different impact work of 1.4kN bit weight
冲击前让球齿紧贴着岩石表面,再给球齿一个冲击速度,再结合球齿的质量,就得出施加给球齿的冲击功。从图7 可以看出球齿的运动状态,首先球齿因为冲击功的施加会冲击岩石,向岩石内部侵入,当到0.001 s 左右球齿侵入到最大位移处,其最大位移为0.6~0.75 mm;然后球齿受到岩石对其的反作用力大于钻压会使球齿产生向上的位移,0.01 s 左右球齿达到最大的向上位移,为1 mm 左右;随后当钻压给的力把岩石的反作用力抵消完全后,球齿开始向下位移,由于其没有冲击功的加成,球齿不能再冲击到破碎坑的最低点;最后钻压被破碎坑与球齿的反作用力相抵,球齿运动状态达到一个动态平衡。
结合图7 与图8 进行分析,球齿在不同的钻压和相同的冲击功下的位移几乎没有改变,并且随着冲击功的每增大5 J,最大侵入位移也会增加0.03 mm左右,呈线性关系。可以得出能影响球齿破碎岩石的深度主要影响因素是冲击功。

图8 40 J 冲击功不同钻压下球齿位移曲线Fig.8 Spherical tooth displacement curve under different bit pressure of 40J impact work
随着钻压的逐渐增大,球齿受到岩石反作用力导致的上返位移在逐渐减小(见图8),两因素的主要关系呈线性相关。因此,可以得出影响球齿上返位移的主要因素是钻压的大小,冲击功对其影响很小。
2.3.3 岩石破碎范围
对于球齿破碎岩石后,岩石的主要区域按应力的影响作用从中心朝外可以分为岩石破碎影响区、应力影响区,应力消散区[30]。要研究单球齿的影响范围,就是研究应力影响区的范围,需要两个边界值来确定其影响范围的大小。首先确定应力影响范围较小的一个边界,该值确定方法如下:由岩石受到球齿冲击,会导致岩石发生破碎,原因为球齿对岩石的压裂和应力波对岩石的剪切作用所导致的较大的位移,通过对岩石产生较大位移的进行数据采集,从而确定岩石产生岩屑的范围,就是应力影响范围的最小值。见图9,其为岩石破坏产生岩屑和裂纹,从而产生较大位移。
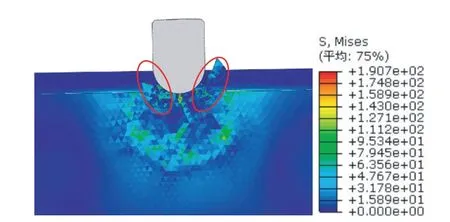
图9 岩石破坏图Fig.9 Rock failure map
图9 红圈中可以看出岩屑从岩石中分离,从而产生了较大的岩屑位移为裂纹扩展区,而处于两红圈之间的区域是受压裂作用发生了较大的岩石破碎,可作为球齿冲击的岩石破碎范围。对岩石破碎范围的选取,产生较大位移的两点的始末的X坐标值分别相减,得到岩石产生岩屑的范围,这个值就是作为此次钻进参数下岩石破碎影响范围的值。图10 对每个钻进参数下岩石破碎范围进行了数据记录分析。
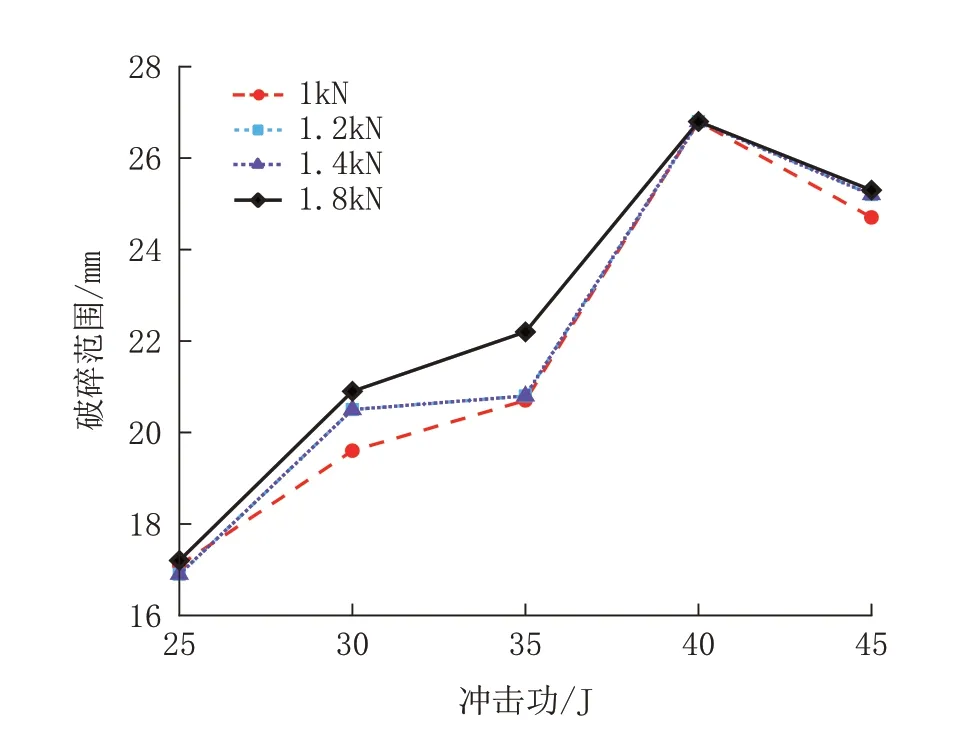
图10 岩石破碎范围曲线Fig.10 Rock breaking range curve
当冲击功为25 J 时,不同钻压下的破碎范围都为17 mm 左右,随着冲击功的增加破碎范围也在变大,但是当冲击功为40 J 时出现了破碎范围转折点,并且破碎直径都在27 mm 左右,破碎范围也开始发生下降,可以从中得出结论,当冲击功达到一定值时继续增大冲击功,会对球齿破碎岩石的范围造成负面影响,不利于球齿破碎岩石表面。可以得出结论:对于单球齿的岩石破碎范围,钻压对其影响不大,冲击功选取40 J 时,可以使其达到最大破坏直径,为26.8 mm,利于球齿破碎岩石。
2.3.4 岩石应力影响范围
对影响范围较小边界值的研究是从岩石产生岩屑的范围来分析的,现在将对岩石受冲击应力波从而产生的应力值来分析影响范围较大边界值。见图11,当球齿冲击岩石时,接触的瞬间球齿会把球齿的动能转化为其它的能量的形式释放出去,冲击应力波是一个主要释放途径,其会对球齿下部的岩石进行压裂作用,对球齿周围的岩石进行应力剪切来破碎岩石。半球形的应力波随着球齿的冲击在岩石中传播,并且随着离球齿距离越远岩石中的应力波也会发生衰落,最后随着时间而消散。冲击过程中岩石中的应力值会随着应力波的变化而变化,因此要准确地研究出岩石应力影响范围较大边界值,就要确定岩石应力值处于峰值应力的时刻。

图11 应力波的扩散Fig.11 Diffusion of stress waves
图12 分别对球齿冲击岩石整个阶段的4 个时间点进行岩石应力的数据分析。黑色曲线对应为冲击岩石前期的应力曲线,根据X坐标显示,其应力整体处于100 MPa 以上的范围是最大的,正是因为冲击应力波还未开始消散,正处于峰值应力;再观蓝色、绿色和紫色曲线,其对应的分别是冲击前中期、中期和末期的3 个阶段,其应力整体大部分处于100 MPa 以下,主要原因是应力波在岩石中传递时被消耗了大部分能量,所以对于要选取应力峰值的时间点应该是冲击的较前期的阶段,此时应力波还没有被消耗,可以较为准确地得到应力影响范围较大边界值。
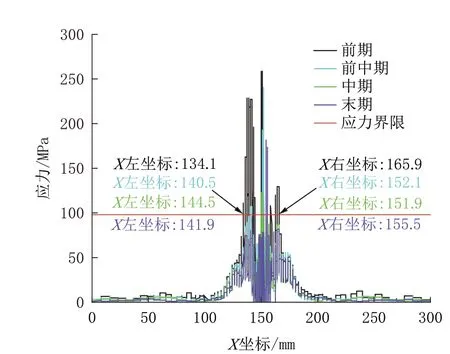
图12 不同时间岩石应力曲线Fig.12 Stress curves of rocks at different times
当岩石的应力值达到抗压强度,岩石会发生破坏,但是不达到抗压强度岩石也会受到应力波的影响,而发生强度下降,图12 的红色横线为应力界限,岩石应力在界限之上视为发生强度下降,得出岩石应力值与应力界限相交的X坐标的值,对应的X坐标的范围为应力影响范围。但对于岩石开始产生强度下降的这个应力界限值,现今没有一个确切的理论来表明,为求应力界限值,本文以岩石的抗压强度120 MPa 为基准,取岩石抗压强度的0.8、0.7、0.6 倍作为应力界限,最后再通过数据分析找出最符合布齿经验结论的应力界限作为标准。
图13 是以96 MPa 为应力界限所得到的应力影响范围曲线,在钻压为1.2 kN,冲击功为30 J 时对应最大的影响范围为43.4 mm,不同钻压下的曲线的趋势都是先增后减,最后趋于平缓。分析可知,对于球齿的钻进,并不是钻压与冲击功越大越好,无论岩石破碎影响范围还是应力影响范围都呈金字塔形状,原因主要是当超过一定的冲击功后,冲击产生的能量大部分不是释放在应力波对球齿两侧的剪切破坏,而是释放于正下方岩石的压裂破坏。

图13 应力界限为96 MPa 下应力影响范围Fig.13 Stress influence range under the stress limit is 96MPa
对应力影响范围的分析,首先对于钻进参数的选取,钻压取1.2 kN 左右,冲击功取30 J 左右,应力影响范围最大,有利于破碎表面岩石。再对应力影响范围进行分析,当0.8 倍抗压强度时,应力影响范围为43.4 mm;当0.7 倍抗压强度时,应力影响范围为53.9 mm;当0.6 倍抗压强度时,应力影响范围为58.6 mm。根据他人经验所得,球齿间的间距尽量为1.5~2 倍的球齿的直径[31],因此进行球齿间距的估算为间距应为27~36 mm 之间,应力界限为96MPa 所得的应力影响范围43.4 mm 对应的球齿间距接近,后续将以96 MPa 作为应力界限。
在单齿冲击碎岩模拟中,随着钻压与冲击功的增大,岩石的破碎体积在不断增大,但破碎比功不会随冲击功的增大而减小,在35 J 左右取得最小值;破碎范围会先增加,当冲击功达到40 J 时,破碎范围开始减小;应力影响范围会先增加,当冲击功达到30 J时,影响范围发生转折,最后趋于稳定。球齿侵入岩石的深度随冲击功的增加成线性增加,但受钻压影响较小。据此,确定较优秀的参数组合,钻压为1.2 kN、冲击功为30 J,能造成岩石较大破碎和较大范围岩石的强度下降。
3 双球齿冲击碎岩数值模拟
3.1 双球齿破碎范围研究
对于双球齿的研究首先要从两种不同的运动方式出发(见图14),一种是圈距即径向距离,另一种是间距即周向位移。采取单齿仿真所得钻进参数,以最优单球齿应力影响范围43.4 mm 作为起始距离,4 mm 为增量,考虑到球齿处于不同圈数的位置,其转速是不一样的,因此设置常见的回转速度8 r/min,由于在单次冲击,时间很短,球齿走过的弧线位移可近似于直线位移,因此对球齿添加线速度来模拟球齿切削,径向方向球齿以最外围两圈进行研究,周向方向球齿以最外围圈进行研究,最外围球齿距中心轴线为300 mm,线速度为0.3 m/s;较内一圈距中心轴线为256.7 mm,线速度为0.28 m/s。

图14 双齿布齿示意Fig.14 Double tooth layout diagram
3.1.1 不同圈距下破碎范围研究
对于不同圈距下的球齿,在同一回转速度下,线速度不相同,如图15 所示,两球齿破碎范围的趋势为随圈距的增加破碎范围先增后减再有小幅度增幅;最高点对应的圈距为47.4 mm 处,线速度较大的球齿破碎范围为25.8 mm,线速度较小球齿破碎范围为22.5 mm。

图15 不同圈距下破碎范围Fig.15 Breaking range under different ring distance
3.1.2 不同间距下破碎范围研究
对于不同间距下的球齿,在同一回转速度下,线速度相同,如图16 所示,当在两球齿间距为43.4mm 时,两球齿对岩石破坏直径最大,前球齿破碎范围为24.8 mm,后球齿破碎范围为22.9 mm,原因为切削时后齿产生了向前的冲击应力波与前齿的应力波相叠加,加大了前齿的破碎范围;随着间距的增加呈递减的趋势,原因为间距的增加会使两球齿造成的应力波对岩石的强度下降的作用降低,碎岩效果也随之降低。
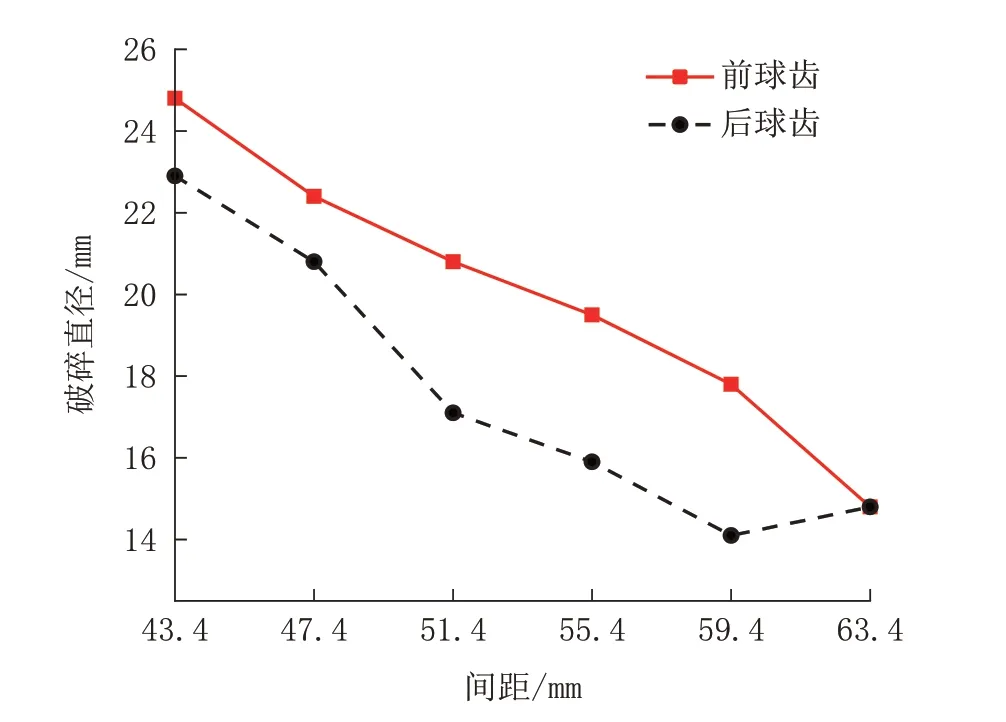
图16 不同间距下破碎范围Fig.16 Range of breakage under different spacing
3.2 双球齿应力影响范围研究
3.2.1 不同圈距下应力影响范围
对于双齿冲击钻进,要研究双球齿造成的影响范围,就要对球齿中间的距离进行研究。岩石受两球齿的应力的分布为:两球齿处应力值大,分别向球齿周围发生下降。根据岩石受应力影响会发生强度下降的原理,从图17(a)可知,当圈距为47.4 mm 时,两球齿的中间部分的应力大部分都处于应力界限之上,表示岩石发生了较大面积的强度下降;从图17(b)可知,当距离为51.4 mm 时,其中间部分有一部分处于应力界限之下,表示中间部分受应力影响较小。其它圈距下的应力曲线,大部分都处于应力界限之下,不做考虑,因此圈距的大小取47.4 mm 左右能让球齿中间大部分的岩石发生强度下降,从而让球齿更容易冲击切削岩石。
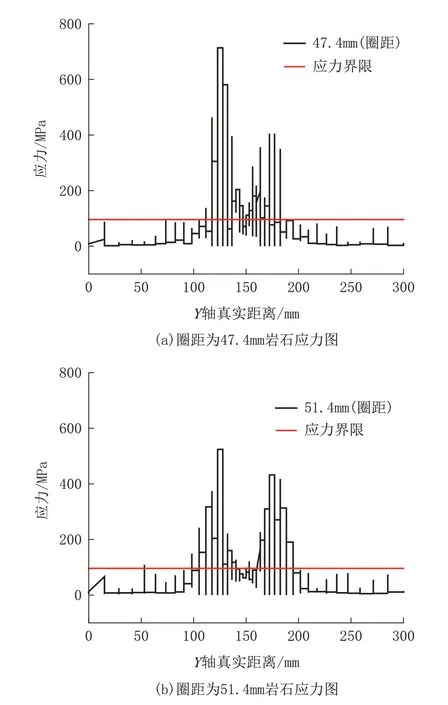
图17 不同圈距下应力影响范围Fig.17 Influence range of stress at different turn spacing
3.2.2 不同间距下应力影响范围
见图18,岩石受两球齿冲击切削应力的分布为:两球齿冲击位置处应力有峰值,分别向周围发生下降。见图18(a),当间距为51.4 mm 时,两球齿的中间部分的应力大部分都处于应力界限之上,表示岩石产生大面积的强度下降;见图18(b),当间距为55.4 mm 时,其中间部分有一部分处于应力界限之下,表示中间部分受到两球齿的应力影响较小;其它间距下的应力曲线,大部分都处于应力界限之下,不做考虑,因此间距取51.4 mm 能使大部分的岩石发生强度下降,使球齿更容易冲击切削岩石。
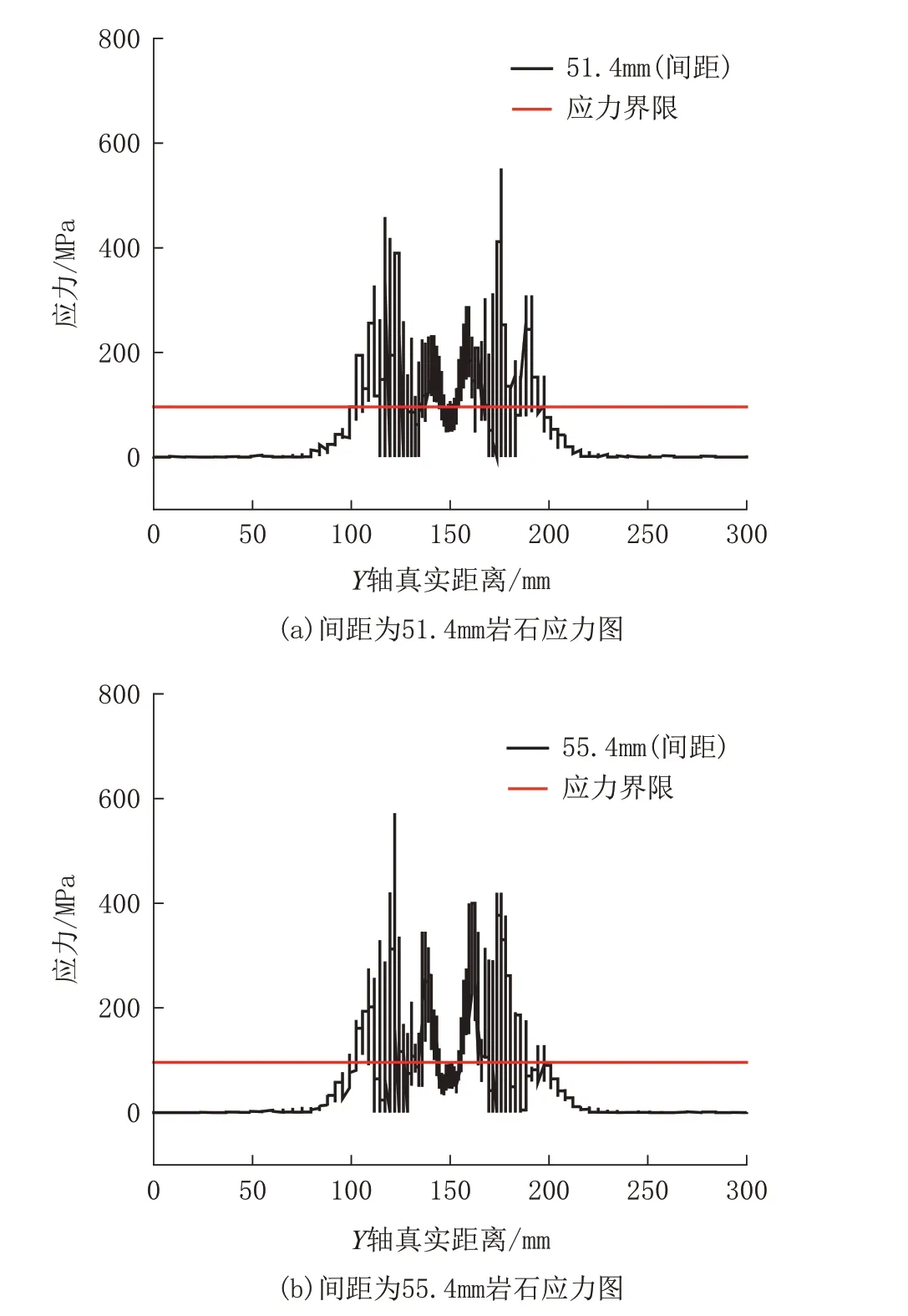
图18 不同间距下应力影响范围Fig.18 Range of breakage under different spacing
通过对上述双齿碎岩仿真研究分析,确定双球齿在钻压为1.2 kN 与冲击功为30 J 的钻进参数下,根据破碎范围与应力影响范围得出的较优的圈距与间距。圈距选取47.4 mm,其破碎范围与应力影响范围都较为优秀。间距选取43.4 mm 时,可对球齿中间岩石造成较大范围的破碎;间距选取51.4 mm时,可对岩石造成大范围的强度下降。
3.3 布齿方案设计
得出球齿圈距与间距,进行钻头球齿布齿,见图19,考虑到钻头形状与球齿不同位置磨损,对圈距与间距进行调整,具体布齿方案如表2 所示。
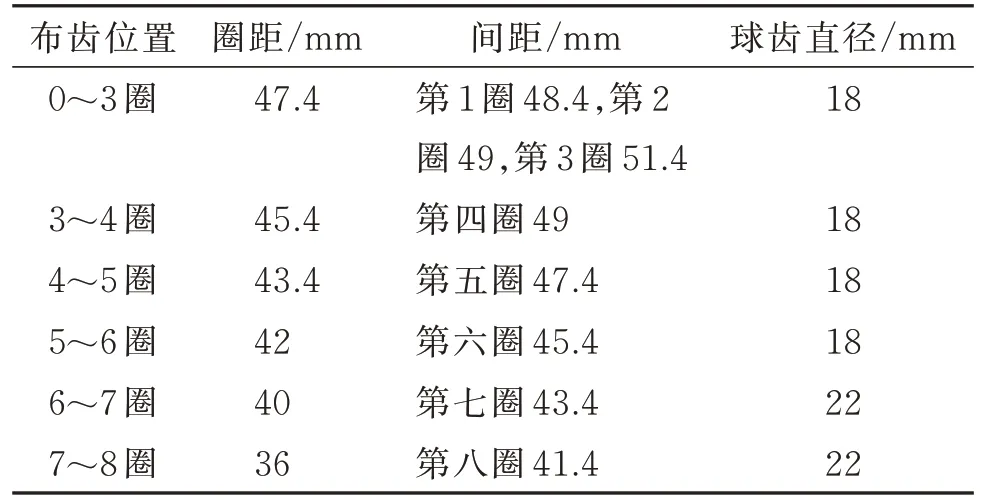
表2 布齿方案表Table 2 Tooth layout scheme table
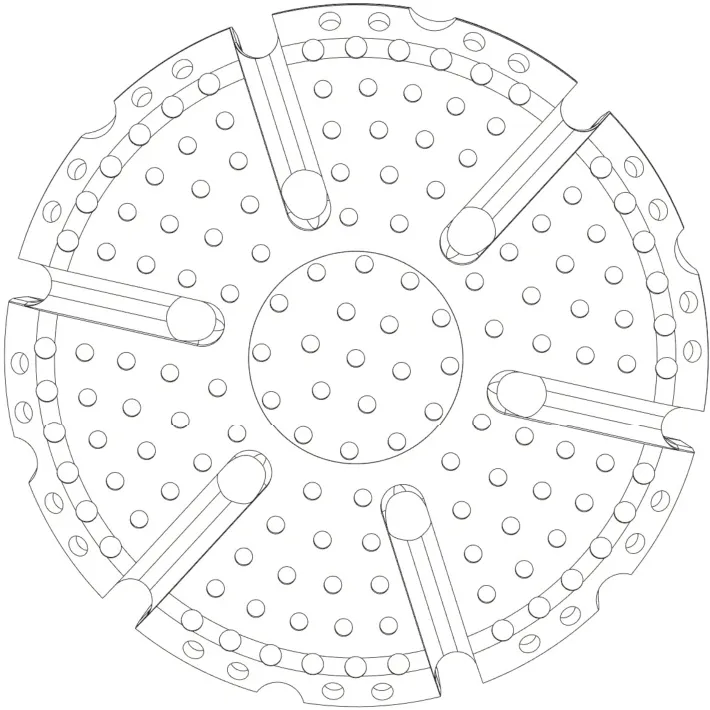
图19 钻头布齿图Fig.19 Drill tooth layout diagram
4 结论
本文通过ABAQUS 仿真软件,对单球齿与双球齿在不同钻进参数下冲击切削岩石进行了模型建立与数值模拟,从不同方面研究分析球齿对岩石的破坏,得到了破碎比功、破碎范围和应力影响范围等在不同钻进参数下的变化规律,并生成对应的曲线图进行分析比较,结论如下:
(1)单齿碎岩仿真从整体到纵向再到横向展开研究,对破碎比功、应力影响范围等曲线进行对比分析,确定较优秀的参数组合。当钻压为1.2 kN,冲击功为30 J 时,对岩石的破碎的效率较高,球齿入岩的位移可达0.67 mm,并根据应力界限得出应力影响范围为43.4 mm。
(2)通过在较优钻进参数下双球齿冲击切削模拟,确定了较为优秀的圈距与间距,圈距取47.4 mm,间距取43.4~51.4 mm。
(3)在平面钻头上进行布齿方案设计:钻头中间部分圈距取47.4 mm、间距取51.4 mm 左右;再向外圈布齿,球齿圈距适当缩小,间距逐步缩小到43.4 mm,保证较外圈球齿磨损与应力不会过大,既保证钻进的效率,也保证钻头使用寿命。
