面向河道保护的冲淤演变规律分析

祝天新

(德州市丁东水库运行维护中心，山东 德州 253500)

黄河冰凌灾害问题在历史上以孕灾环境复杂、突发性强、难以防治而成为我国冬春季节江河中极为突出的自然灾害，给两岸人民带来了巨大的经济损失[1]。随着河流上修建水库后，上游河道的水位升高，过水面积加大，流速减缓，使挟沙能力降低，黄河来水来沙量的大小直接关系到黄河口门附近海域的冲淤演变，致使黄河河段出现了新的冲淤演变规律[2]。所以，对河道冲淤情况进行分析，研究一种河道淤积预测方法来分析冲淤演变规律对防洪的影响十分重要。传统的河床冲刷和淤积演化研究主要采用泥沙平衡法、实测断面法、河相关系法、河工模型法和数值模拟法等流量条件下的水位变化方法；一些学者基于最小熵生成和最小能耗率原理、Mann-Kendall检验法、采用线性趋势法、水体指数法等提取凌汛致灾因子蕴含的持续性、突变性规律，对河床的冲刷和淤积演化进行了分析[3-4]；但是，基本上没有学者通过建立水动力模型来研究河道冲淤演变规律变化。基于此，此次研究将采用经验公式法、沙量平衡法以回归模型方法对河道冲淤量进行计算，分析冲淤变化规律；通过检验计算方法、回归模型方法和实测断面方法计算年均冲淤量，来对河道的淤积和冲刷状态进行预测；最后，通过HEC-RAS软件建立黄河山东河坝下河道一维水动力模型，对典型洪水、设计洪水等进行数值模拟，研究河道冲淤变化规律对黄河山东段河道洪水的影响。

1 河道冲淤演变规律即冲淤预测方法研究

1.1 河道总体冲淤情况和变化趋势研究

河床冲淤演变是一个比较复杂的过程，变化很大程度上与河流的来水来沙条件以及河流的边界有关[5]。研究将以山东黄河菏泽至东营河段为对象，通过沙量平衡法和断面法对河段冲淤量进行计算，分析河道的冲淤演变规律，并以演变规律为基础，采用不同的方法来进行河道冲淤厚度的预测。研究河道山东黄河菏泽至东营河段的基本特性见表1。

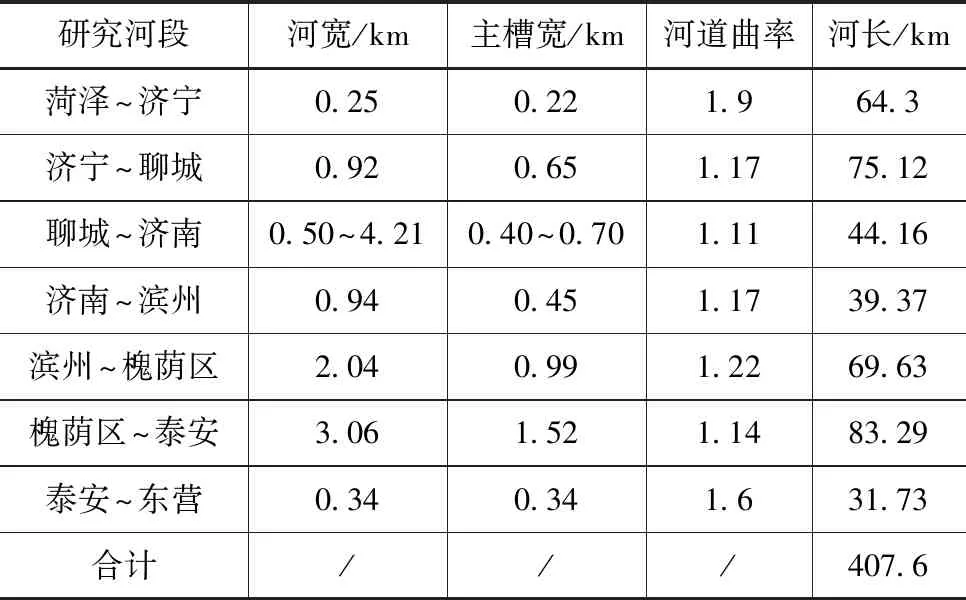
表1 研究河段的河道基础信息

由表1可知，菏泽～济宁、泰安～东营河段的河槽较窄，弯曲率较高，代表河槽受两岸高地约束，主干较为稳固、淤沙堆积少，无需进行冲淤分析。济宁～聊城河段，心滩发育，支流多，河床治理工程进展缓慢，河床崩塌严重，为不稳定的分汊型河床。滨州～槐荫区河段是一条冲积平缓、沙质、抗冲性能差、心滩稀少、边滩发育、险情频发的河流，是一条弯道型河流。槐荫区～泰安河段具有宽、窄、宽、浅、流态紊乱、沙质河床抗冲刷能力弱、冲淤起伏大、主流摇摆、险情频发等特点，是一条游荡型河流[6]。

在河床冲淤变化计算中，河道大断面实测法和输沙平衡法[7]是最常用的2种方法。输沙平衡法又被称为输沙率法，指某一时段内水体泥沙数量的动态相对保持平衡。即在一定时段内输入与输出水体沙量之差等于水体内沙量的变化率。输沙平衡方程如公式(1)所示[7-8]。

ΔWs=Wsj+Wsz+Wsp+Wsf-Wsc-Wsy

(1)

式中，ΔWs—河道冲淤量，kg；Wsj—河段的进口沙量，kg；Wsz—支流沙量，kg；Wsp—排水沟排沙量，kg；Wsf—黄风积沙沙量，kg；Wsc—河段的出口沙量，kg；Wsy—河段引沙量，kg。

输沙平衡法的优势在于，该方法具有时间和空间上良好的连续性和完整性。但由于受引退水数据的限制和测量误差的影响，导致该段泥沙平衡方法的计算结果不能像断面方法那样精确、可靠[9]。利用断面法进行断面间冲淤量计算的公式为：

(2)

式中，ΔV—相邻的2个断面间的冲淤量，kg；ΔL—相邻的2个断面间距，m；Su和Sd—相邻的上、下2个断面间的冲淤面积，m2。

断面法的优势为：①因为测试断面布置的间隔很小，而且冲淤量的计算值只与起始状态相关，而与中间过程无关，不存在累计性误差，所以可以得到精确可靠的河道冲淤量的计算结果。②能反映河床冲淤变化规律[10]。

1.2 河道冲淤预测方法及洪水一维河道模型设计

此次研究还将根据计算分析得到的冲淤规律和实测资料，通过河段来沙系数和单位冲淤量建立多元回归模型方法和利用1.1节的断面法计算多年的平均冲淤量，进行河道冲淤预测。研究以《黄河流域综合规划》中选定的代表性系列为参考，以1985—1995年11a的实测水沙资料为数据，进行黄河山东段2023—2033年的冲刷和淤积预测[11]。研究将依据2010—2020年黄河山东段水沙观测数据，构建泰安站泥沙输移速率与下游河床含沙量之间的多变量回归模型，并利用该模型对下游河床进行验证，回归关系式为：

(3)

河道来沙系数是指河流含沙量与流量的比值，主要反映河道输沙能力与水沙变化关系，来沙系数越小，表明在相同的流量或水流输沙能力条件下，相应的沙量就越小，从而使河道出现冲刷情况，相反，则会造成河道淤积情况[12]。

同时，研究将以实测大断面和研究的河道冲淤变化规律为基础，基于HEC-RAS(Hydrologic Engineering Center-River Analysis System)软件建立黄河山东段河道一维水动力模型，对典型洪水、设计洪水等进行数值模拟，研究河道冲淤变化规律对黄河山东段河道洪水的影响[13]。HEC-RAS是一种可用于恒定和非恒定一维水利计算的河道系统分析软件。HEC-RAS的主要功能有：恒定流水面线的计算，非恒定流水流的模拟，动边界下的泥沙输移以及水质分析。该系统还能自动生成断面形态图、水流和水位变化曲线、复合河道的立体剖面图等多种分析性图形，采用数值模拟计算方法进行水动力过程研究的基本流程包括数据预处理、数值模型嵌套以及结果数据后处理。研究设计的一维河道水动力模型的计算流程如图1所示。

图1 一维水动力模型计算流程

由图1可知，首先，研究通过实测断面资料提取出河道的地形情况，通过相关控制站水位和流量达到边界和初始条件，并根据边界、断面及河网文件构建水动力模型；其次，设计模型参数，并通过实测水位对比分析进行参数的调整；最终计算得出河道的最高水位线，得到一维水动力模型。此次研究将根据济宁～泰安2010年的实测控制站水位、流量数据和实测大断面资料数据为模型构建资料，设计相关参数，河道糙率济宁～济南为0.019～0.037，济南～泰安为0.016～0.039，模型的初始水位设计为：在进行模型计算时，河道最下游一个断面的实测水位，模型设定计算时间步长为30s，输出结果的时间步长为1h。

2 河道冲淤演变规律即冲淤预测结果分析

2.1 河道冲淤情况和变化规律结果分析

研究以1979—2021年黄河山东河段的来沙数据资料为基础，根据济宁至泰安河段的入沙和引沙数据，通过输沙平衡法对3个时间阶段的冲淤情况进行计算和分析，3个时间阶段为跋山水库、青峰岭水库投运时期(1979—1995年)，跋山水库、青峰岭水库和老岚水库共同投运时期(1996—2015年)和近期(2016—2022年)[14-15]，输沙平衡法计算年均冲淤量结果见表2。

表2 输沙平衡法计算年均冲淤量结果 单位：1011kg

由表2可知，在1979—1995年时段内，济宁～济南和济南～泰安河段均处于淤积状态，即黄河山东河段均处于淤积状态，年均淤积0.345×1011kg；1996—2015年时段内，济宁～济南河段年平均冲淤量为-0.123×1011kg，处于微冲状态，济南～泰安河段年平均冲淤量为0.135×1011kg，处于微淤状态，全河段整体年均冲淤量为0.012×1011kg，处于微淤状态；近期2016—2021年时段，全河段处于冲刷状态，年均冲淤量为-0.109×1011kg，济宁～济南河段处于微淤状态，济南～泰安河段处于冲刷状态。同时，提高输沙平衡法计算得到的1979—1995年时段的年均冲淤厚度：济宁～济南河段为0.061m，济南～泰安河段为0.0182；1996—2015年时段，济宁～济南河段年均冲淤厚度0.2829m，济南～泰安河段为-0.145m；2016—2022年时段，济宁～济南河段年均冲淤厚度0.0158m，济南～泰安河段为-0.0251m。为了更加直观地分析黄河山东河段冲淤量的变化规律，研究将对1979—2022年的年均冲淤量和累计值进行分析，河段的历年年均冲淤量累计变化如图2所示。

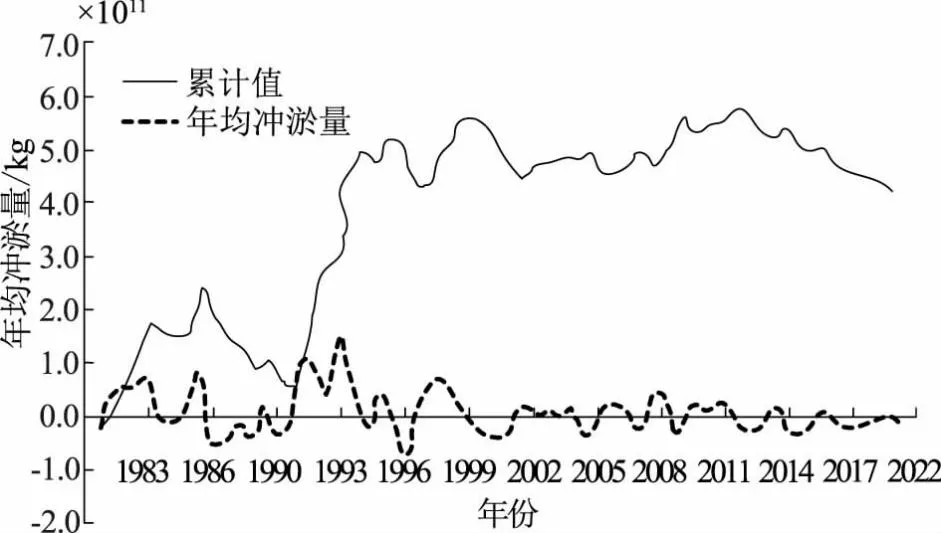
图2 黄河山东河段年均冲淤量累计变化图

由图2可知，年均冲淤量有明显波动，波动范围均在-2～2之间，在1996年时年均冲淤量达到最低，为-0.103×1011kg，表明河段呈冲刷状态；在1993年时，年均冲淤量达到最高，为1.345×1011kg，为淤积状态；整体年均冲淤累计值有明显的波动，在1991年时，年均冲淤累计值最小，为0.796×1011kg；在1985—1991年时段内，累计值呈下降趋势，表明该时段河段主要成淤积状态；在2000年时，年均冲淤量达到最大值，为5.763×1011kg；自2002年以来，年均冲淤量较稳定，主要以冲刷为主。

2.2 河道冲淤预测及河道冲淤对防洪的影响分析

研究将以年均冲淤变化规律为基础，以1985—1995年的实测水沙资料为数据，进行黄河山东段2023—2033年的冲刷和淤积情况预测，通过回归模型方法、经验公式方法和实测断面法对河段冲淤预测结果进行计算，计算结果见表3。

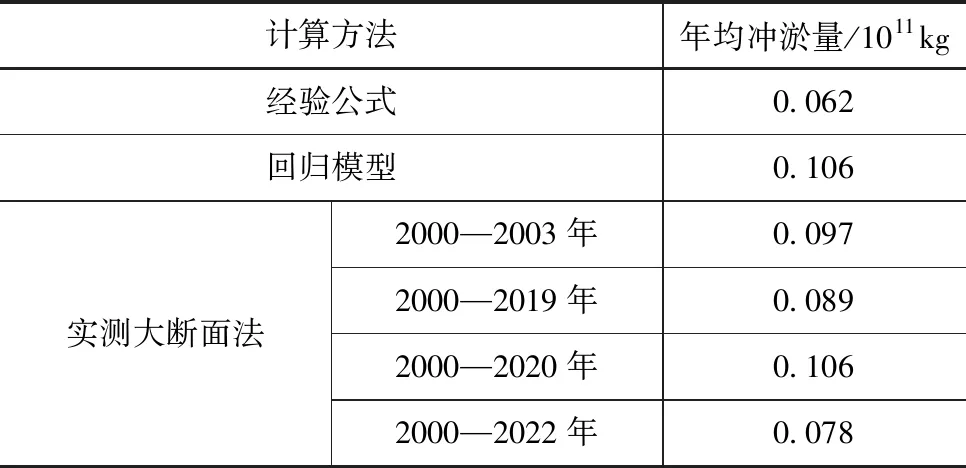
表3 黄河山东段冲淤预测结果

由表3可知，回归模型计算的年均冲淤量预测值为0.106×1011kg，经验公式方法计算的预测值为0.062×1011kg，通过实测断面法计算的年均冲淤量预测值相差不大，其中2000—2003年时段预测的冲淤量最高为0.106×1011kg，2000—2022年时段预测的冲淤量最低为0.078×1011kg。经验公式计算值较小，不符合实际情况，将不选用该值进行冲淤预测。回归模型与实测断面法2000—2020年间的年均冲淤预测值相等，所以研究将选择2000—2020年的实测断面法计算的年均冲淤量0.106×1011kg，为黄河山东河段年均冲淤量的预测值。研究将以年均冲淤量预测值为基础，对黄河山东济宁～泰安各个河段的年均冲淤量和年均冲淤厚度进行预测，预测结果见表4。

表4 黄河山东河段年均冲淤厚度预测结果

由表4可知，济宁～聊城河段年均淤积量为52.63×107kg，年均冲淤厚度为0.007m；聊城～济南河段年均淤积量和年均淤积厚度值均最小，分别为8.28×107kg和0.003m；济南～滨州河段的年均淤积量为100.73×107kg，年均冲淤厚度为0.008m；滨州～槐荫区河段的年均淤积量为387.92m3，年均冲淤厚度为0.011m；槐荫区～泰安大桥河段均淤积量和年均淤积厚度值均最大，分别为485.47×107kg和0.012m；全河段的年均淤积量为550.12×107kg，年均冲淤厚度为0.011m。由于2010年黄河山东河段发生了洪水事件，此次研究将以2010年洪水过程为基础，通过研究设计的一维水动力模型设计洪水，并将设计的洪水水位线与实测的2010年洪水水位线进行对比分析，水位线对比结果图如图3所示。

图3 黄河山东河段洪水水位线对比

由图3可知，图中深泓线为沿河流方向最大水深处的连线，深泓线波动较大，且波动不影响水位线的高度；模型设计水位线与实测最高水位线走向较为平缓，且水位线高度相差不大，模型水位线低于实测最高水位线，最大相差为1.6m。通过表2的年均冲淤量计算结果可知，1996—2015年时段内，黄河山东河段处于淤积状态，淤积量为0.012×1011kg，淤积厚度约为0.23m。黄河山东河段因河床部分泥沙淤积而形成的小流量洪峰，使河道的断面具有比实际情况更高的水位，水位上升进一步导致洪水的发生，容易造成洪水冲刷河岸，增加洪水灾害对人民财产安全的危害。

3 结论

传统的河床冲淤演变分析方法只通过计算冲淤量来分析河道断面形态，没有考虑到河道冲淤变化对防洪的影响，研究将通过检验计算、回归模型和实测断面方法对河道的淤积和冲刷状态进行预测，并通过HEC-RAS软件构建河道一维水动力模型来计算分析河道的冲淤演变规律。结果显示，黄河山东河段年均冲淤量的预测值为0.081×1011kg；研究设计的模型水位线低于实测最高水位线，最大相差为1.6m，即淤积情况下河道断面具有比实际情况更高的水位，易加重洪水对河岸进行冲刷的可能性。同时，此次模型没有考虑闸、坝、桥梁等人工节点的作用，今后的研究可以加上人工节点的设置。