基于灰色系统理论和神经网络的呼吸机故障预测模型的建立与研究

张金波

随着人类历史进程的发展，越来越多未知疾病时刻威胁着人类的生存，进入新世纪以来，严重急性呼吸综合征肺炎（severe acute respiratory syndrome coronavirus，SARS）、中东呼吸系统综合征肺炎（respiratory syndrome coronavirus in the Middle East，MERS）及新型冠状病毒肺炎（coronavirus disease 2019，COVID-19）在全球大爆发的背景下，呼吸机等生命支持类医疗设备在应对重大公共卫生突发事件中的作用得到广泛的认可[1～3]。 在现代临床医学中，呼吸机作为一项人工替代自主通气功能的有效手段，已普遍用于各种原因所致的呼吸衰竭、大手术期间的麻醉呼吸管理、呼吸支持治疗和急救复苏中[4]。在现代医学领域，特别是危重症医学领域中呼吸机是疾病治疗、救援、急救不可或缺的重要组成部分[5]。在临床治疗中，呼吸机故障事件的发生不仅会影响患者治疗效果，更有甚者会危及患者生命安全。因此，如何对呼吸机使用现状进行把控，对其潜在故障进行有效预警是现代医疗设备管理人员面临的重大机遇和挑战。

纵观医疗设备维修管理的发展过程，医疗设备的维修主要由事后维修、预防性维修和状态维修三个部分组成，预防性维修是各级医疗机构重要的管理手段之一；经验表明，预防性维修可以在一定范围内降低医疗设备故障，延长医疗设备生命周期[6，7]。然而，笔者发现， 针对医疗设备的预防性维修大多使用按时、周期性预防性维修或周期性巡检，而有针对性地预防性维修应该建立在医疗设备故障可能发生概率认知的基础上。 如何对医疗设备潜在故障进行合理、科学的预测，是各级医疗机构医疗设备管理人员面临的严峻挑战之一。笔者提出一种建立在灰色神经网络理论基础上的医疗设备故障预测模型，并使用呼吸机故障数据为研究对象对模型进行计算和预测，以期为医疗设备的故障预警、个性化预防性维护和管理提供参考依据。

1 材料与方法

1.1 实验材料

选择笔者所在医院现行使用的呼吸机马克涡轮故障数据及呼吸机每年设备故障数据为研究对象。呼吸机开机自检后，使用福禄克Fluke117C 数字万用表对呼吸机马克涡轮供电电压进行采样， 采样间隔为5 min，采样时间为120 min，呼吸机马克涡轮供电电压采样值见表1 所示。 选取采集的前16 组马克涡轮供电电压拟合模型，使用后9 组数据作为模型预测检验数据集，进而评估不同模型的预测精度。同时，收集并整理2013 年至今笔者所在医院同型号呼吸机维修记录，以呼吸机启用时间为计数“零”点，记录每年设备故障数据，并计算设备故障率作为故障数据集，各年故障数据集为（0.17，0.19，0.67，0.98，1.45，2.37，3.44，4.12，5.17，6.66），使用前8 组数据对各模型进行拟合计算，并使用拟合后的模型对后两组数据进行预测。

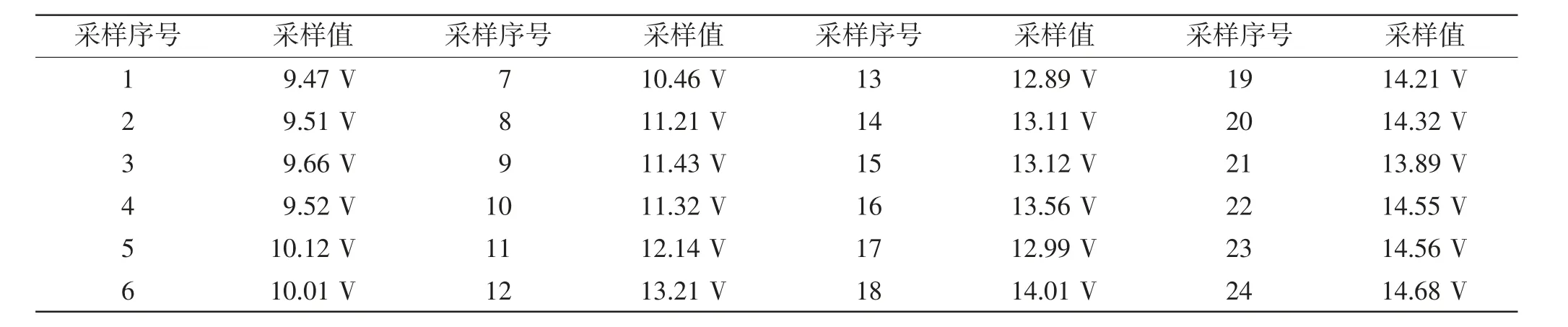
表1 呼吸机马克涡轮供电电压采样值Tab.1 Sampling values of supply voltage of ventilator Mark turbine

1.2 方法

1.2.1 灰度神经网络模型

1.2.1.1 GM（1，1） 灰色系统理论是控制理论与决策论相结合的产物，它是一种研究小样本、贫瘠信息不确定问题的新方法；灰色系统理论包含部分已知信息和部分未知信息的小样本，主要通过贫瘠的部分已知信息，提取、开发有用的信息，进而对未知信息进行预测的过程[8]。 灰色模型（grey model，GM）是灰色系统理论的研究基础，设已知信息X(0)= （x(0)（1），x(0)（2），x(0)（3），…，x(0)（n）），该模型实现过程如下：对X(0)进行一阶累加，形成新的数字序列：

令Z(1)为GM（1，1）的背景值，由X(1)得到：

GM（1，1）均值表达式为：

根据文献[9，10]，采用最小二乘法可计算参数a 和b，可得到X(1)预测模型为：

由公式（1）可计算X(0)序列值

值得注意的是，当k ≤n 时，xˆ(0)（k） 为GM（1，1）对原序列值的拟合值，当k ＞n 时，xˆ(0)（k） 为原序列的预测值。

1.2.1.2 优化GM（1，1） 经验表明，系统或医疗设备故障的特征通常趋势都是未知或隐性的，而GM（1，1）使用的背景值为X(1)临近数据均值，可能会造成背景误差，进而会造成预测结果的误差[11]。 对GM（1，1）优化的方法最常见的是双重改进灰色模型（double improved grey model，DI-GM）[12]。

DI-GM 需要对背景值和初始值进行改进， 其中背景值z(1)（k）为：

根据最新信息优先原则，将原数据累加序列的终止值作为序列首值，此时公式（4）可优化为：

由公式（5），可计算X(0)序列值。

1.2.1.3 灰色神经网络组合模型 通常信息贫瘠问题是单一模型信息提取不足而造成拟合、预测不足等问题出现的主要原因之一。 因此， 将DI-GM 与Levenberg Marquardt 反向传播 （Levenberg Marquardtback propagation，LM-BP）结合形成组合预测模型[13]，分为并联式预测模型（parallel prediction model，PPM）、串联式预测模型（series prediction model，SPM）。

（1）PPM：首先定义模型预测精度序列，令：

计算预测精度序列pr 的均值和均方差：

定义DI-GM 与LM-BP 预测并联加权系数分别为δ1和δ2，计算如下：

根据PPM[14]，可得PPM 预测结果为：

（2）SPM：在LM-BP 神经网络结构设计中，加入灰化层和白化层，其中灰化层对数据输入进行GM 灰化处理，白化层的作用是恢复LM-BP 模型输出[15]。

对公式（4）右侧除以系数1 + exp（-ak），然后再乘系数1+exp（-ak）得：

令ω11=a，ω21=-x(0)（1），ω22=，ω31=1+exp（-ak），ω32=1+exp（-ak），令加入旁路输入（1+exp（-ak））。 根据BP 神经网络性质，建立SPM 拓扑结构（图1）。

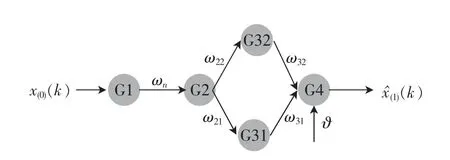
图1 SPM 拓扑结构Fig.1 Topological structure of SPM

对于离散型预测模型，预测精度是指预测值与实际值的密集或者离散程度，在模型精度检测中常用的精度检测指标有最大相对误差 （maximum relative error，RE_max)、 平均相对误差 （mean relative error，RE_mean）、 均方根误差 （root mean squard error，RMSE）、平均绝对误差（mean absolute error，MAE）和拟合度（R-squared）[16～18]。

（1）RE_max,是一个范围值，指的是可能出现的最大的那个不确定的值，用来描述预测值与实际值的离散最大程度，RE_max 计算如下：

相应地，RE_mean 计算如下：

（2）RMSE 又称标准误差， 用来检测预测值和原始值数据离散程度的变量，其值越小，模型拟合效果越符合实际情况。 RMSE 计算如下：

（3）MAE 是绝对误差的平均值，表征预测值与实际值平均值之间的离散程度。 MAE 不会出现正负相抵消的情况，因而MAE 能更好地反映预测值误差的实际情况：

（4）R-squared 正常情况下取值范围为0 ～1，描述的是输入变量对输出变量的相近程度。在单变量回归分析中R-square 越大，越接近1 越好：

1.2.3 数据分析方法

使用MATLAB 对各模型进行建模，使用前16 组马克涡轮供电电压及前8 年呼吸机故障数据进行拟合计算，并使用拟合后的模型对后9 组马克涡轮供电电压及第9、10 年呼吸机故障数据进行预测， 计算各模型的RMSE、MAE 及R-squared 值。 对GM、DIGM、PPM、SPM 计算的结果与实际结果残差值处理。

然而站上演讲台，一切都不一样了。3个多小时的论坛上，David侃侃而谈，详述新西兰葡萄酒的趋势与变化；两个半小时的大师班，David悉心讲解新西兰每个产区、每款葡萄酒的特色与亮点，大师班的开始高呼三声毛利语，激起了整个课堂的气氛；1个多小时站在品鉴会的入口背景板处与葡萄酒爱好者合照、交流，聚光灯的照射下汗水一次次浸湿手帕；4个小时的晚宴上，致开幕词不忘感谢活动的每一位组织者……晚上11点，第十届金樽奖颁奖典礼落下帷幕，David穿过走廊，慢慢地走回房间。留给他与广州相处的时间不多，第二天的中午他又要登上18个小时的飞机，回到新西兰，开始新一周的工作。

1.2.4 精度判断标准

使用MATLAB 对各模型进行建模， 对各模型的残差序列进行自相关检，P ＜0.05 判定模型的存在序列相关；对各模型残差序列进行异方差检验，P ＜0.05为差异有统计学意义，判定模型建立较好，可以进行预测。

1.3 统计学方法

采用SPSS 24.0 对各模型差值结果进行统计学分析，对各模型马克涡轮供电电压及年设备故障率拟合值和预测值与实际值的差值以均数±标准差表示，模型间采用配对t 检验，以双侧95%可信区间（confidence interval，CI）为统计标准。 P ＜0.05 为差异具有统计学意义。

2 结果

2.1 基于灰色系统理论和神经网络的呼吸机涡轮电压预测结果分析

2.1.1 模型的建立与精度分析

采集的呼吸机涡轮电压为一组平稳的时序序列，利用统计软件MATLAB 2019a 使用平稳的时序序列对各模型进行建模，并使用采集的呼吸机涡轮电压前16 组数据对各模型进行拟合计算（图2）。 通过运行GM、DI-GM、PPM 及SPM， 各模型R-squared 分别为0.954、0.979、0.983、0.984，各模型的解释能力较强；各模型拟合的RMSE 分别为2.294 V、1.330 V、1.106 V、0.967 V，SPM 拟合程度最优、 准确率最高； 类似的，SPM 的MAE 最小，也反映了模型准确率最高。

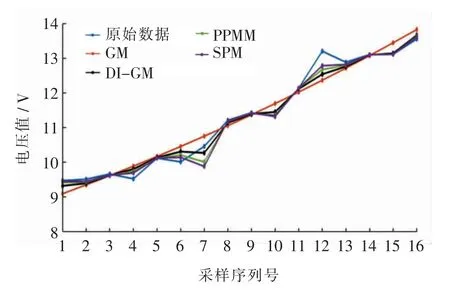
图2 各模型对呼吸机马克涡轮电压拟合结果Fig. 2 Diagrams of fitting results of various models for ventilator turbine voltage

2.1.2 模型预测与检验

通过MATLAB 对各模型进行预测分析， 以采集的呼吸机马克涡轮电压前16 组数据为原序列进行拟合计算，以采集的呼吸机马克涡轮电压后8 组数据为预测序列进行预测分析， 结果GM、DI-GM、PPM 及SPM 预测RE_max 分别为17.91%、7.16%、4.81%及3.96%，RE_mean 分别为10.06 %、4.02 %、2.30 %及1.62%，PPM、SPM 预测效果良好，SPM 预测效果最优（图3）； 各模型预测的R-squared 分别0.362、0.685、0.793 及0.890，SPM 预测结果更符合预测序列分布；各模型预测的RMSE 分别为8.939 V、3.829 V、2.230 V及1.579 V，预测MAE 分别为1.429 V、0.572 V、0.323 V及0.225 V， 预测结果均显示SPM 预测准确率最高（表2）。

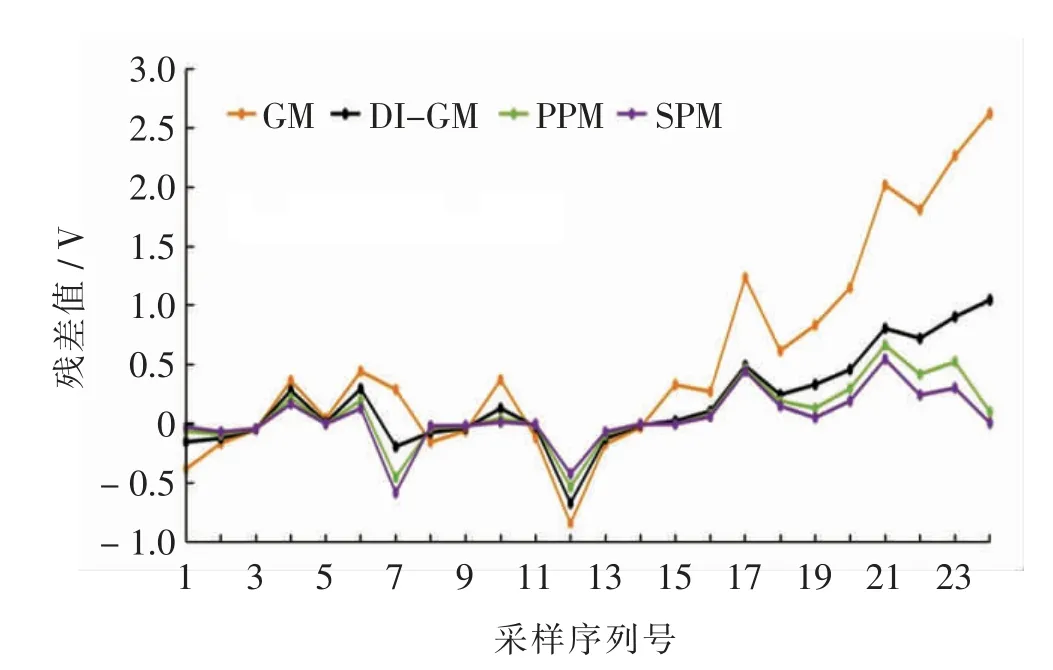
图3 各模型预测呼吸机马克涡轮电压值与实际值的残差序列图Fig.3 Residual sequence diagram of predicted ventilator turbine voltage values and actual values for each model

表2 各模型预测精度计算结果Tab.2 Calculation results of prediction accuracy for each model

使用MATLAB 对GM、DI-GM、PPM 及SPM 拟合计算结果及预测结果的优劣作进一步检验，为消除时序信息序列对检验方法的影响，计算各模型计算值与实际值的残差序列（图3）。 对各模型的预测值残差序列进行自相关检验，自相关结果（χ2= 8.091、8.791、9.445、10.235，P ＜0.05），模型不存在自相关；同样地，对各模型残差序列进行异方差检验，异方差结果（t=1.266、1.178、0.918、1.276，P ＞0.05）， 各模型建立较好，可以进行预测。 各模型残差小提琴图见图4，SPM对呼吸机马克涡轮供电电压预测结果相对GM、DIGM 预测精准度显著提高，提高效果具有统计学意义（P ＜0.001）；PPM 对呼吸机马克涡轮供电电压预测结果相对GM、DI-GM 预测精准度亦有显著提高， 提高效果具有统计学意义（P ＜0.05）。

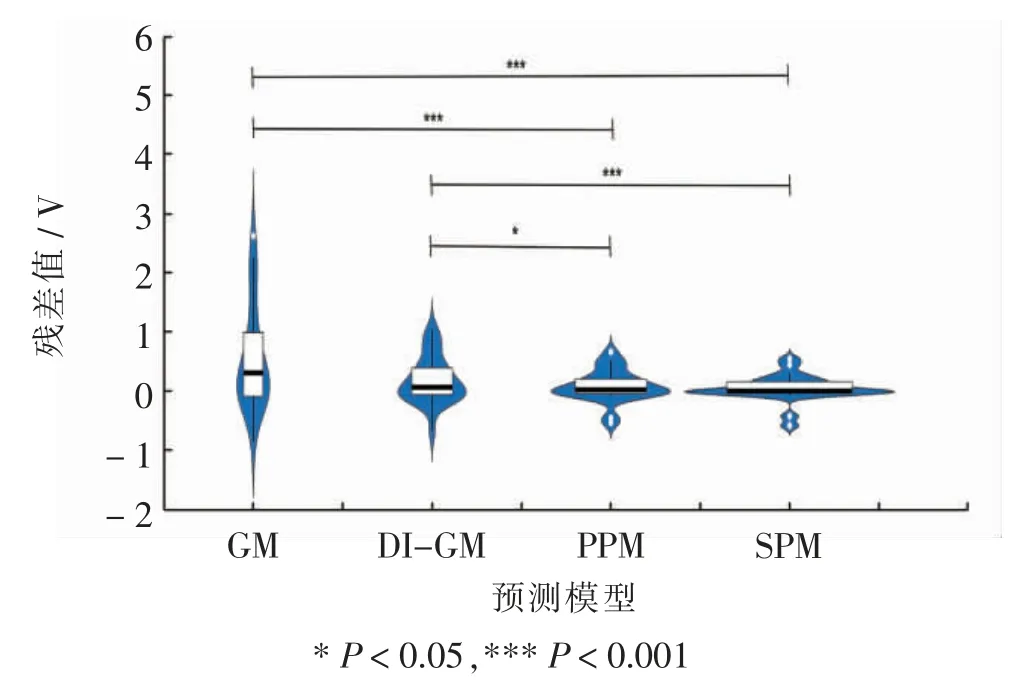
图4 各模型预测马克涡轮电压值残差小提琴图Fig.4 Residual violin chart of turbine voltage values predicted by various models

2.2 基于灰色系统理论和神经网络的呼吸机故障率预测

2.2.1 模型的建立与精度分析

收集并整理笔者所在医院2013 年至今同型号呼吸机维修记录，以呼吸机启用时间为计数“零”点，记录每年设备故障数据作为时序序列， 使用MATLAB 2019a 对各模型进行建模，并使用整理的前8 组时序数据对各模型进行拟合计算（图5）。 通过拟合计算，运行GM、DI-GM、PPM 及SPM 的R-squared 分别为0.772、0.968、0.991 及0.995，DI-GM、PPM 及SPM 的解释能力较好； 各模型拟合的RMSE 分别为0.278、0.170、0.129 及0.110，SPM 拟合优度最高；类似地，SPM绝对误差的MAE 最小，也反映了SPM 准确率最高。

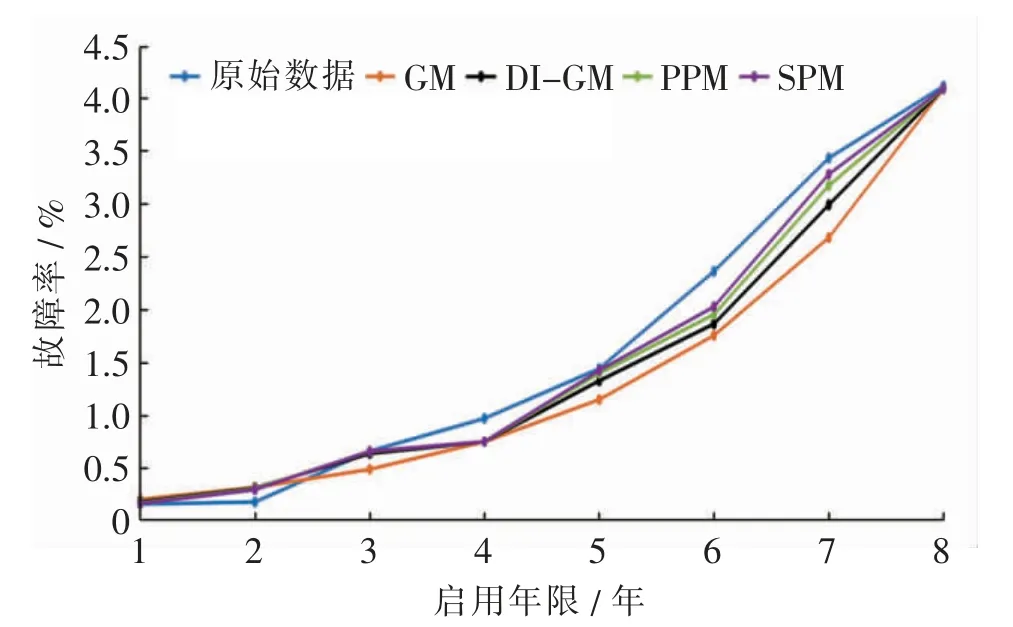
图5 各模型对呼吸机故障率拟合结果Fig.5 Fitting results of various models for ventilator failure rate

2.2.2 模型预测与检验

使用4 种模型对呼吸机故障率后两组数据进行预测分析，GM、DI-GM、PPM 及SPM 对呼吸机使用第9、10 年故障率预测值的相对误差分别为20.69 %、9.55 %、4.68 %、2.17 %及42.74 %、21.13 %、7.88 %、2.52%，SPM 预测准确率最高、效果最优。

进一步对使用各模型进行精度检验，计算各模型计算值与实际值的残差序列（图6）。 对各模型的预测值残差序列进行自相关检验，GM、DI-GM、PPM 及SPM 自相关检验结果（χ2=4.779、6.125、8.889、9.197，P ＜0.05），4 种模型不存在自相关；DI-GM、PPM 及SPM 异方差检验结果（χ2= 1.443、1.678、1.256，P＞0.05），3 种模型拟合结果偏离实际设备故障率较小，可用于模型预测，GM 异方差检验结果（t=3.449，P ＜0.05），残差偏离结果程度较大，预测效果较差。 各模型预测呼吸机故障率残差小提琴图见图7，SPM 预测结果相对GM、DI-GM 预测精准度显著提高， 提高效果具有统计学意义（P ＜0.01）；PPM 预测结果相对GM、DIGM 预测精准度亦有显著提高，提高效果具有统计学意义（P ＜0.05）。

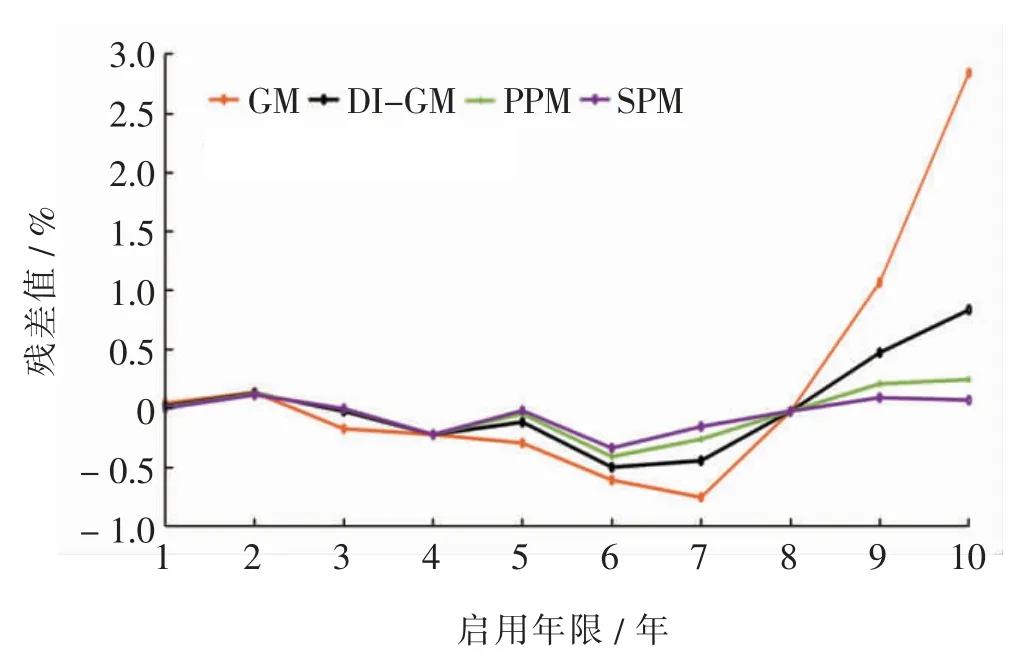
图6 各模型预测呼吸机故障率与实际值的残差序列图Fig. 6 Residual sequence diagram of predicted ventilator failure rate and actual value for each model

图7 各模型预测呼吸机故障率残差小提琴图Fig. 7 Residual violin chart for predicting the failure rate of ventilators by various models

3 讨论

针对呼吸机，“轻预防、重维修”的管理模式仍是大多数医疗机构维修管理模式，如何正确地了解呼吸机寿命规律，对呼吸机故障进行合理预测也是困扰医疗设备管理人员的一大难题[19～22]。

近年来， 针对呼吸机故障模式识别的研究有很多，同时也取得了一定的研究成果。 2020 年陈艳等[23]提出一种基于数据挖掘技术的粗糙神经网络模型，采集呼吸机使用环境因素、 电气因素及气路因素数据，并建立8 输入3 输出的粗糙神经网络模型。模型训练集呼吸机故障模式灵敏度、 特异度及准确率分别为87.8%、85.6%、91.1%， 测试集呼吸机故障模式准确率达85.0%。 2020 年徐咏梅[24]提出一种进化算法，并将其应用于麻醉呼吸机活瓣关闭不全故障自动检测，使用虚拟数据对模型进行测试，测试结果显示普通神经网络方法检测识别RMSE=0.19795； 进化算法方法检测识别RMSE=0.24195。 2021 年马建川等[25]采用故障树和贝叶斯网络的方法对呼吸机常见故障进行分析， 利用贝叶斯网络对呼吸机故障进行定量分析，结合使用实际维修案例进行验证，结果显示，该方法得到的推理结果与实际结果相符性达到84.54%。陈娜群设计了一种医疗器械相对位置定位方法，通过无线传感器网络定位技术，利用已知的少量的传感器节点构建无线传感器网络，从网络中提取传感器位置特征，建立支持向量机（support vector machines，SVM）模型、Softmax 模型及Decision Trees 模型， 当传感器个数达到8 个时， 各模型位置正确识别率分别为95.65%、96.43%及97.76%[26]。

笔者所在医院的某品牌呼吸机是一款当下使用最广泛的无创呼吸机之一， 该无创呼吸机采用低赖性可变速马克涡轮。 马克涡轮转速最大可达40000 r/min，可提供最大3.92 kPa（40 cmH2O）水平压力，具有低惯性、可变速、响应速度快等特点，是该呼吸机易损核心部件之一。 当马克涡轮正常工作时，马克涡轮发动机驱动板供电电压为8.5 ～13.5 V 的直流电压。随着呼吸机累计使用年限的增加， 当供电电压高于13.5 V 时，马克涡轮会出现噪声大、卡杠、转速小等现象，通常临床表现出气端气体温度升高、压力水平降低等， 此时需对马克涡轮进行预防性维护或更换，以避免电压上拉损坏发动机驱动板和影响呼吸机治疗。临床经验表明，呼吸机在投入临床使用时，医疗设备故障多呈现“浴盆故障曲线”，排除医疗设备初期的偶发故障，医疗设备故障在一定程度上呈现逐年递增的趋势。 了解呼吸机故障发生趋势，对合理安排呼吸机预防性维护有着十分重要的意义。

利用GM 适用于小样本、少数据问题和神经网络模型非线性信息处理能力强的优点， 笔者在GM（1，1）及DI-GM 优化预测模型的基础上，提出了两种灰色理论结合神经网络的组合模型，即SPM 和PPM。通过收集笔者所在医院现行使用的呼吸机马克涡轮供电电压时间序列数据、 呼吸机故障率时间序列数据，通过已知时间序列数据的计算，完成了GM、DIGM、PPM 及SPM 的预测结果对比。 研究结果表明：相对传统模式识别模型，灰色神经网络组合模型可使用少样本、少数据进行计算、预测；灰色神经网络组合模型减少了算法的时间复杂度和空间复杂度，且可以更好地分析和处理数据， 数据处理结果稳定性更强；此外，灰色神经网络组合模型兼具GM 和BP 神经网络模型优点， 能够更准确地预测工程装备的故障趋势，为预测性维修决策提供科学的理论依据。

4 结论

灰色系统理论适用于小样本贫瘠数据，能够较好地对线性问题进行拟合和预测，灰色理论结合神经网络模型可以很好地对非线性信息加以处理。基于灰色理论与神经网络相结合模型既可以对呼吸机故障率进行准确的预测，同时还可以对呼吸机关键部件的小样本故障进行精准的预测， 可为呼吸机预防性维护、维修提供理论依据，也可在一定程度上降低责任工程师工作强度，提高呼吸机临床使用效率，值得进一步研究和推广。