青海湟水流域基于改进的MLP 大气加权平均温度模型研究

赵利江，杨海鹏，许超钤，赵健赟

1. 长安大学 地质工程与测绘学院，西安 710054；

2. 青海省基础测绘院，西宁 810016；

3. 青海省地理空间信息技术和应用重点实验室，西宁 810016；

4. 武汉大学 测绘学院，武汉 430079；

5. 青海大学 地质工程系，西宁 810016

1 引 言

湟水流域是青海省政治、经济、文化和交通中心，流域内人口数为312 万，占全省人口数的60.2%；工农业总产值为143 亿元，占全省的54.2%。20 世纪90 年代以来随着气候增暖、降水减少、地表蒸发量的不断增加，湟水流域气候干旱化程度进一步加快，异常天气（雪灾、干旱、洪涝、冰雹等）发生次数明显增加（戴升等，2006）。尤其是2022年8 月发生的持续降雨，引发了大通县的山洪和泥石流，造成4 人死亡，27 人失联。而水汽是降水发生的最直接因素，因此，研究湟水流域的水汽变化及其与强降水的相互关系，对指导防灾减灾工作具有十分重要的现实意义。

可降水量（precipitable water vapor，PWV）是从地面直到大气顶界的单位面积大气柱中所含水汽总量全部凝结并降落到地面可以产生的降水量，是反映大气水汽含量主要技术指标。近年来，随着国家卫星导航定位基准站网和各省卫星导航定位基准站网的逐步建立，基于全球导航卫星系统（global navigation satellite system，GNSS）反演PWV逐步成为研究热点（马进全等，2019；张鹏等，2018；王洪栋，2018）。PWV精度受大气加权平均温度（Tm）影响。Tm可以使用探空站的大气垂直气象要素计算，但受限于站点数量较少且时间分辨率较低，难以满足实际应用需求，因此，传统研究通常用Tm数据建立模型，此类模型主要分为回归模型和经验模型两种。回归模型通过分析Tm与地表气象要素的相关关系采用回归分析等方法建立，最早的是利用北美 13 个探空站两年的探空记录建立的Bevis 式模型（Bevis 等，1992）。但因其系数具有季节和地理的限制，在其他地区使用误差较大。为提高本地模型精度，有研究基于我国探空数据建立了东部地区的Bevis 式模型（李建国等，1999；刘焱雄等，2000）；有研究利用Tm与地表气温、气压、露点温度、水汽压相关关系，建立了本地的多因子模型，结果表明增加因子数能够提高Tm的估计精度（刘旭春等，2006；周国君和潘雄，2006；李国翠等，2008）。上述回归模型计算Tm均需要地表气象要素，难以满足实时水汽的计算需要。因此，不需要气象参数的经验模型陆续出现，如GWMT-D（He 等，2017）、全球气压温度3（global pressure and temperature 3，GPT3）（Landskron 和Bohm，2018）、GGTm（Huang 等，2019）等，其中，GPT3 模型具有开源、易操作、格网分辨率和精度高的特点，是目前使用最为广泛的经验模型。GPT3 模型出现之后，将积日（day of year，DOY）引入区域加权平均温度模型，所得精度优于 GPT3（莫智翔等，2021）。杨飞等（2022）优化后的GPT3 模型中误差达到3.52 K。但经验模型精度往往低于回归模型（Ding，2020）。随着大数据的发展，有研究利用神经网络基于气温、气压、水汽压、高程、纬度、积日等建立了大气加权平均温度模型（谢劭峰等，2022）。相比传统模型精度有一定的提升，却未考虑大气加权平均温度的长期变化趋势。

为进一步研究提高大气加权平均温度模型的精度，本文利用欧洲中期天气预报中心（European Centre for Medium-range Weather Forecasts ，ECMWF）的全球气候第五代再分析（the fifth generation ECMWF atmospheric reanalysis，ERA5）数据集和大气逐层数据，考虑大气加权平均温度的年际变化，基于多层感知器（multilayer perceptron，MLP）方法建立了湟水流域大气加权平均温度模型，并与已有的Bevis 式、双因子、多因子、GPT3、改进的GPT3 模型、谢劭峰等（2022）方法六种模型进行了比较验证。结果表明，本文所建立的改进的MLP 模型具有更高的精度。

2 数据来源

湟水流域只有西宁1 座探空站，因此仅使用探空数据建立的Tm模型虽然在局部有很高的精度，但无法满足整个流域的计算需求。本文从ECMWF 收集了湟水流域2010~2020 年的大气逐层数据、ERA5 数据集中1950 年以来的陆地地表气温数据，主要包括大气逐层气压、温度、位势高度、比湿和地表温度、气压、露点温度等参数。在国家气象科学数据中心（http://data.cma.cn/）收集了11 座气象站的地表气温、气压、露点温度等数据。从美国怀俄明大学官网（http://www.weather.uwyo.edu/）下载了2010~2022 年西宁站探空数据，其中包括气压、高度、地面温度、露点温度、比湿、相对湿度等参数，用于检验模型精度。另外，收集了流域内30 m 分辨率的数字高程模型，用于获取格网平均高程。为了弥补气象站数量的不足，使用陆地地表气温数据补充了6 个格网点。气象站及格网点分布，如图1 所示。

图1 站点分布Fig.1 Distribution map of stations

3 研究方法

3.1 Tm 计算原理

在利用GNSS 观测数据进行水汽反演过程中，首先要对GNSS 原始数据进行处理以获取天顶总延迟（zenith total delay，ZTD），并用获取的估值减去由于大气引起的天顶静力学延迟（zenith hydrostatic delay，ZHD），从而得到与水汽相关的天顶湿延迟（zenith wet delay，ZWD）。可降水量与天顶湿延迟之间的关系如下：

式中，PWV 为可降水量，mm；Π为转换因子，其与大气加权平均温度Tm函数关系为

式中，Rv为水汽气体常数；k2、k3为常数。Rv=461.522 J/（kg·K），k2′=22.1±2.2，k3=3.739（±0.012）×105K2/hPa。

大气加权平均温度Tm与大气水汽压ei、大气温度Ti、层高dh的关系可使用ECMWF 提供的逐层大气参数离散积分：

式中，ei、Ti分别为第i层大气的平均水汽压（hPa）和平均气温（K）；hi为第i层大气厚度，m。hi由势高作差得到，由于层间势高差与高程差相差较小，因此，本文在数据处理时，直接使用势高差代替高程差。由于ECMWF 提供的大气逐层数据、陆地地表气温数据中没有水汽压，需要使用比湿由式（4）或露点温度由式（5）求得

3.2 多层感知器

MLP 是一种前向结构的人工神经网络，由多个节点层所组成，其中，第一层为输入层，最后一层为输出层，中间部分为一个或多个隐含层。除输入节点外，每个节点都是一个带有非线性激活函数的多输入单输出神经元。结构如图2 所示。

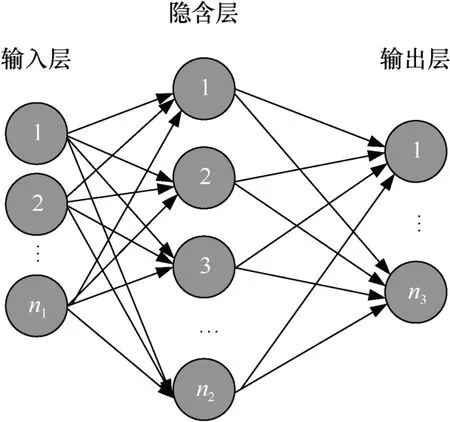
图2 MLP 结构示意Fig.2 Architecture of multi-layer perceptron network

3.3 精度评价指标

使用平均偏差Sbia和均方根误差Srm表示新模型与参考值间的离散程度：

式中，N为匹配样本总量；yi为模型估计Tm值，K；zi为探空数据实测Tm值，K。

相关系数Corr 表示两个样本的相关关系：

式中，X为被检验数据，包括地表温度（K）、水汽压（hPa）；Y为Tm样本数据，K。

4 实验与分析

4.1 Tm 变化特征

由大气逐层数据、陆地地表气温数据中提取了湟水流域11 座气象站、6 个格网点的136562 个样本数据，计算了全部样本数据的Tm值。图3（a）描述的是2010~2020 年湟水流域的日均Tm随时间的变化情况，湟水流域年均Tm约270 K，最高点约280 K（DOY 为210），最低点约250 K（DOY 为365），具有明显的季节性变化。图3（b）描述的是2010~2020 年湟水流域的年均Tm随时间变化情况，除了季节性变化之外，该流域Tm年均值具有一定的年际变化：2010~2012 年下降；2012~2016 年回升；2016~2020 年下降。因此，本文将积日和累计日（cumulative day，CD）作为建模参数。

图3 湟水流域2010~2020 年大气加权平均温度变化情况Fig.3 Changes of atmospheric weighted average temperature in Huangshui basin from 2010 to 2020

4.2 相关性分析

为明确Tm模型参数，本文计算了2010~2020 年湟水流域136562 个样本数据的大气加权平均温度Tm，分析了Tm与地表气温Ts、水汽压es、高程hs、纬度bs的相关性，其中，Ts与Tm相关系数0.934，es与Tm相关系数0.85，均呈正向强相关，因此，建模时应考虑Ts、es。hs、bs对Tm有系统性的影响，如不考虑纬度和高程的变化则模型中会存在一定的系统误差，Tm与Ts、es、hs、bs的相关关系，如图4 所示。

图4 大气加权平均温度与地表气温（a）、水汽压（b）、高程（c）和纬度（d）的相关关系Fig.4 Correlation between atmospheric weighted average temperature with surface temperature (a), water vapor pressure (b),elevation (c), and latitude (d)

4.3 模型结果对比

4.3.1 典型模型对比

为了解不同Tm模型的精度水平，本文利用2010~2020 年湟水流域的ERA5 数据建立了三种有气象要素的线性回归分析模型（Bevis 式、双因子、多因子）、一种经验模型（GPT3）、一种混合模型（改进的GPT3）。并利用均方根误差、平均误差比较和评价了五种传统模型估计Tm的精度，如表1 所示。

表1 传统模型的参数及其内符合精度Tab.1 Traditional model parameters and its internal coincidence accuracy K

（1）在Bevis 式模型的基础上，增加水汽压可使回归模型均方根误差减小17%，进一步增加高程和纬度因子可降低回归模型的平均误差，但均方根误差没有明显降低。

（2）经验模型GPT3 在湟水流域具有较好的适用性，在不需要地表气象参数的条件下平均误差可达0.078 K，标准差2.17 K。

（3）混合模型的均方根误差优于GPT3 和多因子模型，但平均误差有明显增大，需要使用探空数据进一步验证。

4.3.2 改进的MLP 模型

为了进一步提高模型精度，借鉴谢劭峰等（2022）方法的多层感知器原理，本文引入参数——年际变化因子（CD），并结合地表气温Ts、水汽压es、高程hs、纬度bs和DOY 建立了改进的MLP 模型。

（1）选取与Tm具有相关关系的Ts、es、hs、bs、DOY、CD 作为协变量输入到输入层，Tm作为因变量。

（2）将70%数据作为训练集，30%作为验证集，反向优化模型参数，利用2018 年西宁探空站实测Tm评估所建模型的性能。

（3）定义神经网络模型结构，利用试凑法得到模型隐藏层的层数为1、节点数为4。隐藏层激活函数为双曲正切函数，输出层激活函数为恒等函数y=x，损失函数选用误差平方和。

（4）在模型训练中，选取批次训练，优化算法选择标度共轭梯度法。

研究中起点时间为2010 年1 月1 日。相比于谢劭峰等（2022）方法，本模型平均偏差减小50%，均方根误差减小4%，如表2 所示。

表2 MLP 相关的模型参数及内符合精度Tab.2 Model parameters and internal coincidence accuracy based on MLP K

5 精度评价

5.1 基于探空数据的模型精度分析

为客观检验模型精度，使用2010~2022 年西宁探空站实测Tm对Bevis 式、双因子、多因子、GPT3、改进的GPT3 模型、谢劭峰等（2022）方法与改进的MLP 模型进行了评价，结果如表3 所示。考虑了CD因子的本模型均方根误差相比Bevis 式、双因子、多因子、GPT3、改进的GPT3、谢劭峰等（2022）方法分别减小了32%、23%、15%、14%、7%、5%。此外，本模型顾及了地表温度、水汽压、高程、纬度、积日、累计日多种影响因素，模型表现得更稳定，如图5 所示。因此，本模型可以为青海湟水流域GNSS反演PWV 提供更高精度的大气加权平均温度值。

表3 研究所用模型外符合精度Tab.3 Out-of-model coincidence accuracy K

图5 模型残差散点分布Fig.5 Scatter plot of model residuals

5.2 Tm 对PWV 的影响估计

为量化Tm对PWV 的影响，利用式（1）、式（2）分别对П和Tm微分得式（9）、式（10）。Tm取湟水流域年均大气加权平均温度270 K，进一步简化得式（11）。如

式中，σП为转换因子的均方根误差；σPWV为PWV均方根误差，mm。

式中，mTσ为Tm均方根误差，K。

取湟水流域平均湿延迟150 mm。得到各模型计算PWV 精度情况，如表4 所示。可知Bevis 式、双因子、多因子、GPT3、改进的GPT3、谢劭峰等（2022）方法、本模型的Tm误差带给PWV 的影响分别为0.336 mm、0.293 mm、0.267 mm、0.263 mm、0.245 mm、0.240 mm、0.227 mm。

表4 不同方法产生的PWV 误差Tab.4 PWV error of different models

6 结 论

考虑了年际变化因素，本文利用青海湟水流域2010~2020 年大气逐层数据和陆地地表气温数据，建立了适用于青海湟水流域的改进的MLP大气加权平均温度模型，并以2010~2022 年西宁探空站获取的Tm为参考，与已有研究方法进行了精度比较评价，结果表明，平均偏差和均方根误差分别为–0.01 K、2.71 K，均方根误差相比于Bevis 式、双因子、多因子、GPT3、改进的GPT3模型、谢劭峰等（2022）方法分别减小了32%、23%、15%、14%、7%、5%。这证明本文改进的MLP 模型在青海湟水流域的精度要优于已有研究方法，一定程度上能够为湟水流域大气评估研究提供方法参考。